集合と命題第 3 回

命題について

◀

集合の包含関係

必要条件と十分条件

▶

はじめに

「命題」とは，白黒はっきりつけられる主張のことです。 数学では単純な計算をするだけでなく，色々な命題を考えます。

ここは解説だけ読んでも抽象的でよく分からないと思います。 必ず確認問題を通して具体例を見ておきましょう。

目次

命題

▼

命題とは，正しいか正しくないかが明確に（客観的に）定まる主張のことをいいます。 命題が正しいことを真，正しくないことを偽といいます。 命題の内容は，数式だけで表されたり，文章だけで表されたり様々です。

補足 命題になるもの・ならないもの

例えば「\(2 < 1\)」や「有理数は実数である」は命題です。 前者は偽，後者は真と明確に定まりますね。

それに対して，「犬はかわいい」や「\(100\)は大きい」は命題ではありません。 これらが正しいかどうかは判断する人の感性により，明確には定まらないからです。

条件

▲
▼

命題を考える上で重要な概念として，条件というものがあります。 普通に使う日本語ですが，数学では「変数を含む主張で，変数の値を決めたときにその真偽が定まるもの」と定義します。

何だかややこしそうな定義ですが，その意味は普段使う「条件」と同じで，「制約」や「制限」の意味合いを持ちます。 例えば\(x\)を実数とすると，「\(x < 1\)」は条件です。 単に\(x\)というとどんな実数でもありえますが，「\(x < 1\)」という条件があれば，その中で\(1\)より小さいものに限定されます。 これはまさに\(x\)に関する条件ですね。

条件の定義は「どんな変数の値に対しても条件を満たすか判断できる」とも読めます。 あのややこしそうな定義は，条件から曖昧さをなくすために必要なものなんですね。

いくつかの条件を「かつ」と「または」で組み合わせて，新しい条件を作ることもできます。 \(p, q\)を条件とすると，\(p, q\)の真偽に応じて，「\(p\)かつ\(q\)」と「\(p\)または\(q\)」の真偽は次のようになります。

\(p\) \(q\) \(p\)かつ\(q\) \(p\)または\(q\)
真 真 真 真
真 偽 偽 真
偽 真 偽 真
偽 偽 偽 偽

「\(p\)かつ\(q\)」は，\(p, q\)が両方とも真のとき真になります。 「\(p\)または\(q\)」は，\(p, q\)のどちらか一方でも真なら真になります。 日常語の「かつ」「または」と同じ使い方ですね。

仮定と結論

▲
▼

命題には「\(p\)ならば\(q\)」の形のものが多くあります。 これを次のように表します。

\( \begin{align} p \implies q \end{align} \)

このとき\(p\)を仮定，\(q\)を結論といいます。 「\(p\)である」と仮定したとき，「\(q\)である」という結論が得られるということです。

いきなり用語や記号の説明をしましたが，ピンとこないと思うので例を見ましょう。 \(p, q\)は前項で学んだ条件です。 例えば\(x\)を実数とすると，「\(x < 1\)ならば\(x < 5\)」は\(p \implies q\)型の命題です。 この命題で\(x < 1\)は仮定，\(x < 5\)は結論です。 （ちなみに，この命題は真です。\(1\)より小さい数は当然\(5\)よりも小さいですね。）

補足 命題の言い換え

「偶数と奇数の積は偶数である」という命題を考えましょう。 これは\(p \implies q\)型の命題に見えないかもしれません。 しかし\(x, y\)を整数とすると，この命題は「\(x\)が偶数，\(y\)が奇数ならば，\(xy\)は偶数である」と言い換えられます。 つまりこの命題も\(p \implies q\)型です。 仮定が「\(x\)が偶数，\(y\)が奇数」，結論が「\(xy\)は偶数」です。

このように，多くの命題は\(p \implies q\)型です。 そうは見えない命題も，多くは「\(p\)ならば\(q\)」の形に言い換えられます。

この命題は実数を対象にした主張でした。（\(x\)を実数としましたね。） このように命題を考えるとき，それが何を対象にした主張なのかに気を配る必要があります。 こうした「特定の範囲」を考えるのが前回学んだ集合でしたね。 次項で命題と集合を結び付けてみましょう。

命題と集合

▲
▼

前項で，命題には\(p \implies q\)型のものが多いと書きました。 そして\(p, q\)は条件です。 つまり条件の情報をうまく整理すれば，命題についても考えやすくなります。

条件について考えると，対象になるもの全体の中に，条件が成り立つものと成り立たないものがあります。 その理解には，集合の考え方を使うと便利です。

例として，\(x\)を実数としたときの条件「\(x < 1\)」について考えます。 まず，全体集合は実数全体の集合ですね。 その中で条件が真になる部分集合（真理集合といいます）を考えると，次のベン図が描けます。

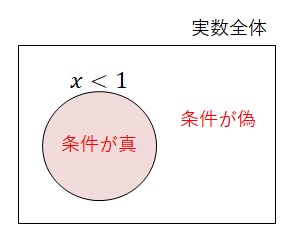
上のように，条件は集合によって表現できました。 では「\(p \implies q\)」を集合で表現するとどうなるでしょうか。 命題には真の場合と偽の場合がありますから，まずは真の場合について考えてみましょう。

ここでクイズです。 \(p\)の真理集合を\(P\)，\(q\)の真理集合を\(Q\)とします。 \(p \implies q\)が真であるとき，\(P, Q\)の包含関係はどうなっているでしょうか？ 次の図の(1)～(4)の中から選んでください。

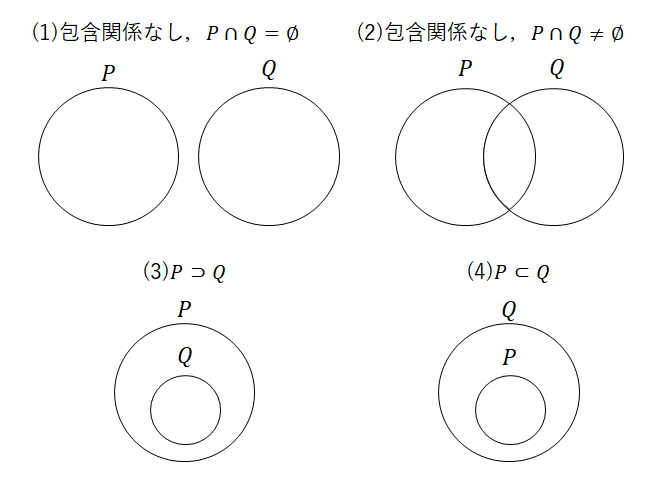
「\(p\)ならば\(q\)」が真ということは，「\(p\)を満たすならば\(q\)を満たす」という意味です。 つまり\(x \in P\)ならば\(x \in Q\)ということになるので，\(P \subset Q\)となります。 ということで，正解は(4)でした！

実は，「\(p\)ならば\(q\)」が真であることは\(P \subset Q\)と全く同じです。 同様に「\(p\)ならば\(q\)」が偽であることは\(P \not \subset Q\)と全く同じです。

補足 \(P \not \subset Q\)

\(P \not \subset Q\)は\(P \subset Q\)でないという意味です。 つまり，\(x \in P\)なのに\(x \not \in Q\)となるような\(x\)が存在するということです。 言い換えれば，仮定\(p\)を満たしても結論\(q\)が成り立たない場合があるということです。

このような\(x\)を「\(p \implies q\)の反例」といいます。 要するに\(p \implies q\)が成り立たない例ですね。 反例が１つでもあれば\(p \implies q\)は偽となります。

このように，命題は集合の包含関係と結び付けて考えることができます。 仮定・結論の真理集合が分かる場合は，ベン図をかくことで，命題の真偽を視覚的に理解できるわけです。

否定

▲
▼

次は「～でない」といった否定について考えましょう。 \(p, q\)を条件，\(P, Q\)をその真理集合とします。

まずは条件の否定について説明します。 条件\(p\)に対して，「\(p\)でない」という条件を\(p\)の否定といい，\(\overline{p}\)と表します。 補集合と同じ記号を使っていますね。 実際，\(\overline{p}\)の真理集合は\(\overline{P}\)（\(P\)の補集合）です。

次に「かつ」と「または」の否定を考えます。 これはその言葉の意味を考えれば分かりますし，真理集合を使っても分かります。 せっかくなので，ここでは真理集合を使って説明します。

まず「\(p\)かつ\(q\)」の否定を考えましょう。 「\(p\)かつ\(q\)」の真理集合は\(P \cap Q\)ですから，その否定の真理集合は\(\overline{P \cap Q}\)です。 ド・モルガンの法則を思い出すと，これは\(\overline{P} \cup \overline{Q}\)ですね。 つまり，「\(p\)かつ\(q\)」の否定は「\(\overline{p}\)または\(\overline{q}\)」です。

同じように考えると，「\(p\)または\(q\)」の否定が「\(\overline{p}\)かつ\(\overline{q}\)」であることも分かります。

もうひとつ否定について確認しておきたいのが，「すべての～」や「ある～」の否定です。 どちらも主張の範囲を表すために頻出する表現です。

このような命題の例に「すべての実数\(x\)について，\(x^2 \geqq 0\)」や「ある整数\(x, y, z\)について，\(x^2 + y^2 = z^2\)」があります。

補足 いろんな表現

「すべての～」と同じ意味を持つ表現はいくつかあります。 例えば「任意の～」や「常に～」，「一般の～」などがあります。 「すべての～」という文字列ではなく，その言葉の意味に注意しましょう。

「ある～」についても同様です。 同類の表現に「～が存在する」などがあります。

補足 全称と存在

高校数学では使いませんが，「すべての～」や「ある～が存在する」を記号で表すことができます。 「すべての～」は\(\forall\)で，「ある～」は\(\exists\)で表すことができます。 それぞれ All ， Exist の頭文字を裏返した記号です。

この記号を使って「任意の実数\(x\)に対して，\(\vert x - y \vert < 1\)となる整数\(y\)が存在する」という命題を記号で表現すると，「\({}^\forall x \in \mathbb{R}, {}^\exists y \in \mathbb{Z} \mbox{ s.t. } \vert x - y \vert < 1\)」となります。 \(\mbox{ s.t. }\)は such that の略で，「\({}^\exists X \mbox{ s.t. } Y\)」で「\(Y\)であるような\(X\)が存在する」という意味になります。

「すべての\(x\)について\(p\)」の否定は，「すべてではない」ということに注意すると，「ある\(x\)について\(\overline{p}\)」となります。 「ある\(x\)について\(p\)」の否定は，「そんな\(x\)はない」ということなので，「すべての\(x\)について\(\overline{p}\)」となります。

意味を考えれば否定がどうなるかは分かりますが，「すべての～」の否定は「ある～」，「ある～」の否定は「すべての～」と機械的に変換できることも分かりますね。

確認問題

▲

次の文章や数式が命題といえるかどうか答えてください。 また，命題といえる場合は，その真偽を答えてください。

  1. \(1\)は\(2\)よりも小さい

  2. 西暦2000年の日本では，消費税率（地方消費税含む）が20%であった

  3. \(x + 1 = 3\)

  4. ある実数\(x\)について，\(x^2 = -1\)

  5. 数学は難しい

答え

  1. 実数の大小関係は客観的に判断できるので，命題です。 \(1\)は\(2\)よりも小さいので，この命題は真です。

  2. 消費税率は法律に規定されており，客観的に判断できるので，命題です。 真偽については調べれば分かりますが，2000年時には5%ですから，この命題は偽です。

  3. この等式が正しいかどうかは\(x\)の値によって変わります。 \(x\)の値を決めるまでは，この等式の正しさは判断できませんから，これは命題ではありません。 このように，\(x\)の値を決めれば真偽が定まるものを「条件」といいます。

  4. どんな実数\(x\)に対しても\(x^2\)は計算でき，\(-1\)と等しいかどうかも判断できます。 したがって，これは命題です。 実数の平方は必ず\(0\)以上ですから，この命題は偽ですね。

  5. 数学が難しいと思うかどうかは人により，客観的に判断できないので命題ではありません。

次の条件の真理集合を実数\(x\)の不等式で表してください。 ただし，(1)の条件を\(p\)，(2)の条件を\(q\)と呼ぶことにします。

  1. \(x\)は正

  2. \(\vert x \vert < 5\)

  3. \(p\)かつ\(q\)

  4. \(p\)または\(q\)

答え

  1. 日本語をそのまま数式に直して\(x > 0\)が真理集合です。 これを\(P\)と呼ぶことにします。

  2. 絶対値をはずして\(-5 < x < 5\)が真理集合です。 これを\(Q\)と呼ぶことにします。

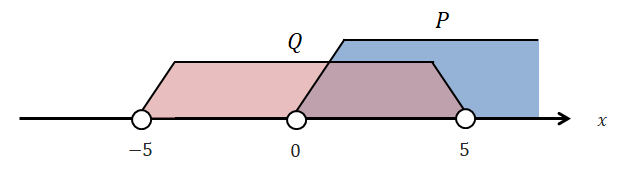
  3. この真理集合は\(P \cap Q\)ですから，\(0 < x < 5\)です。 図で考える場合は，真理集合が無限集合であるため，ベン図は使いづらいです。 数直線を使いましょう。

  4. この真理集合は\(P \cup Q\)ですから，\(x > -5\)です。 図で考える場合は，真理集合が無限集合であるため，ベン図は使いづらいです。 数直線を使いましょう。

集合\(A, B\)（\(\neq \varnothing\)）に対して，次の条件\(p, q\)を考えます。

\(p\)： \(A \subset B\)
\(q\)： \(A \cap \overline{B} = \varnothing\)

  1. \(p\)を仮定，\(q\)を結論とする命題の真偽を答えてください。

  2. \(q\)を仮定，\(p\)を結論とする命題の真偽を答えてください。

答え

  1. \(A \subset B\)を仮定するわけですから，\(A\)の要素\(x \in A\)は，すべて\(x \in B\)でもあります。 ということは，\(x \in A\)でありながら\(x \in \overline{B}\)でもある\(x\)は存在しないわけです。 したがって，\(A \cap \overline{B} = \varnothing\)であり，命題が真であることが分かります。

  2. \(A \cap \overline{B} = \varnothing\)を仮定するわけですから，\(A\)の要素\(x \in A\)は，絶対に\(x \in \overline{B}\)ではありません。 （もしそんな\(x\)があれば，\(A \cap \overline{B}\)は空集合になりませんね。） ということは，この\(x\)は\(x \in \overline{\overline{B}} = B\)であるわけです。 したがって，\(A \subset B\)であり，命題が真であることが分かります。

この問題では，場合分けを省略するために\(A, B\)を\(\varnothing\)でないとしましたが，\(\varnothing\)を許しても(1)，(2)ともに真になります。

また後で学びますが，このように\(p \implies q\)と\(q \implies p\)がともに真であるとき，\(p\)と\(q\)は「同値」であるといいます。 このとき，実は\(p\)と\(q\)は全く同じであり，同じことを別の言い方で表現しているだけであることが分かります。

次の条件および命題の否定を答えてください。

  1. \(x < 1\)

  2. \(x = 1\)かつ\(y \neq 1\)

  3. \(x + y \geqq 1\)または\(x^2 + y^2 = 3\)

  4. すべての自然数\(x, y, z\)と\(3\)以上のすべての整数\(n\)について，\(x^n + y^n \neq z^n\)

  5. ある実数\(x, y\)について，\(x = 2y\)かつ\(x^2 = y\)

答え

(1)～(3)は条件，(4)～(5)は命題ですね。

  1. 否定は「\(1\)より小さくない範囲」なので，\(x \geqq 1\)ですね。

  2. 「かつ」の否定は「または」になるのでした。 答えは\(x \neq 1\)または\(y = 1\)です。

  3. 「または」の否定は「かつ」になるのでした。 答えは\(x + y < 1\)かつ\(x^2 + y^2 \neq 3\)です。

  4. 「すべての～」の否定は「ある～」になるのでした。 答えはある自然数\(x, y, z\)と\(3\)以上のある整数\(n\)について，\(x^n + y^n = z^n\)です。 \(n\)の範囲を表す「\(3\)以上」まで否定して「\(3\)未満」としないように注意してください。 あまり機械的にやり過ぎると間違えるところです。

  5. 「ある～」の否定は「すべての～」になるのでした。 答えはすべての実数\(x, y\)について，\(x \neq 2y\)または\(x^2 \neq y\)です。