前回は集合とは何かということを学びました。 今回は集合が他の集合の一部になっている場合などを考えます。
目次
集合の包含関係
2つの集合\(A, B\)について,ベン図をかくと下図のような状況になっていることがあります。
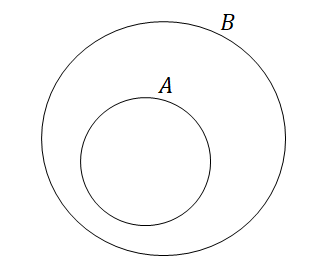
つまり,ある集合が他の集合の中に収まってしまうことがあります。 上図では\(A\)が\(B\)の中に全部収まっています。 このとき,\(A\)は\(B\)の部分集合であるといい,\(A \subset B\)や\(B \supset A\)と表します。 「\(A\)は\(B\)に含まれる」や「\(B\)は\(A\)を含む」とも表現します。
また,このようにある集合が他の集合の部分集合になっているとき,これらの集合の間には包含関係があるといいます。
\(\cap\)や\(\cup\)ほど混乱しないと思いますが,\(\subset\)の使い方についてもコメントしておきます。 この記号は不等号と同じように使えばよくて,記号の開いている側が大きい集合です。
\(A\)が\(B\)の部分集合であるとき,\(B\)の方が大きい集合ですから,\(\subset\)を使って表すと\(A \subset B\)または\(B \supset A\)となるわけですね。
ちなみに,高校数学では\(\subset\)は両者の集合が等しい場合も含むので,不等号でいえば「\(\lt\)」より「\(\leqq\)」に近いです。
ベン図だけで説明しましたが,\(A \subset B\)の定義をちゃんと書くと,「すべての\(x \in A\)について,\(x \in B\)にもなっている」ということです。 \(A \subset A\)であることに注意してください。
\(A \subset B\)かつ\(B \subset A\)であるとき,\(A\)と\(B\)は全く同じ集合になります。 このとき,\(A\)と\(B\)は等しいといい,\(A = B\)と表します。 2つの集合\(A, B\)が等しいことを示すには,\(A \subset B\)と\(B \subset A\)の2つを示さないといけないんですね。
部分集合の中でも,特に\(A \subset B\)かつ\(A \neq B\)であるとき,\(A\)は\(B\)の真部分集合であるといいます。
少し部分集合の扱いを練習してみましょう。\(A\)を偶数全体の集合,\(B\)を\(4\)の倍数全体の集合とします。 \(A\)と\(B\)の包含関係はどうなっているでしょうか? \(A, B\)は次のように書けますね。
まず\(A \subset B\)かどうかを調べましょう。 すべての\(x \in A\)が\(x \in B\)にもなっていれば\(A \subset B\)です。 しかし,\(2\)は偶数なので\(2 \in A\)ですが,\(4\)の倍数ではないので\(2 \notin B\)です。 したがって\(A \subset B\)ではありません。
\(A \subset B\)であるためには,すべての\(x \in A\)が\(x \in B\)でもある必要があります。 なので1つでも例外があれば\(A \subset B\)にはなりません。 例外とはつまり,\(x \in A\)なのに\(x \in B\)じゃないもののことですね。
\(A \subset B\)でないことを証明するには「こんな例外があるよ~」と1つだけ示せば良いわけです。
次に\(B \subset A\)かどうかを調べましょう。 すべての\(x \in B\)が\(x \in A\)にもなっていれば\(B \subset A\)です。 すべての\(x \in B\)は整数\(n\)を用いて\(x = 4n\)と表せます。 これを少し変形すると\(x = 2 \cdot (2n)\)となり,\(2n\)は整数ですから\(x \in A\)にもなっていることが分かります。 したがって\(B \subset A\)となっていますね。
\(A \subset B\)であるためにはすべての\(x \in A\)が\(x \in B\)でもある必要があります。 これをどうやって示せば良いでしょうか?
この証明のためには,まず\(A, B\)がどんな集合なのかきちんと把握する必要があります。 それはつまり,\(A, B\)の要素が満たすべき条件を把握するということです。
ここまで把握できたら,「\(A\)の条件を満たす要素は,すべて\(B\)の条件も満たす」ことを説明すれば,\(A \subset B\)が証明できます。
上の例では,「\(4\)の倍数」の条件を満たす数がすべて「偶数」の条件も満たしていることを説明したわけです。
全体集合と空集合
地球上の生物について研究したいとき,いきなり全生物をまとめて相手にするのは難しいです。 脊椎動物と無脊椎動物に分けて考えたり,霊長類に限って考えたりします。
このとき,考察対象全体の集合は「地球上の生物」でありながら,実際に取り扱う集合は「脊椎動物」などです。
このような考察対象全体の集合のことを全体集合といいます。 数学の例を挙げると,整数を全体集合として偶数について考えたりします。
全体集合をベン図で表すときは,下図のように長方形でかくことが多いです。 図では全体集合を\(U\),その部分集合を\(A\)で表しています。 \(U\)が考察対象の全体で,その中で集合\(A\)を扱うときの図ですね。
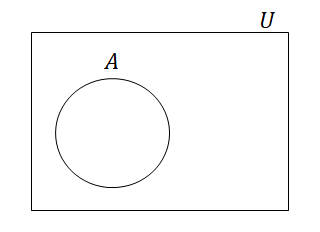
全体集合は考察対象をすべて含む大きな集合ですね。 では最も小さい集合はどんなものでしょうか? 集合はそれを構成する要素の集まりですから,要素が1つもない集合が最小でしょう。
要素を1つも持たない集合を空集合(くうしゅうごう)といい,\(\varnothing\)で表します。 空集合は,すべての集合の部分集合になっていると考えます。
要素が1つもない空集合って何か意味あるの?と思うかもしれません。 空集合は数でいうところの\(0\)みたいなもので,\(0\)と同じく普通に使う集合です。
例えば,偶数全体の集合\(A\)と奇数全体の集合\(B\)に対して,\(A \cap B = \varnothing\)です。 これで「偶数かつ奇数の数なんてないよ」を表せます。
ちなみに,空集合の記号\(\varnothing\)は,\(\emptyset\)という書き方をすることもあり,そのまま「空集合」と読むことが多いです。 いずれにしても,ギリシャ文字の\(\phi\)とは違う記号なので注意です。
補集合
全体集合\(U\)の中で集合\(A\)を考えましょう。 さっきのベン図の状況です。 このとき,全体集合のすべての要素が「\(A\)に属するもの」と「\(A\)に属さないもの」に分かれていますね。 この「\(A\)に属さないもの」の集合を\(A\)の補集合といい,\(\overline{A}\)と表します。
\(\overline{A}\)は「\(A\)バー」などと読みます。 \(\overline{A}\)をベン図で表したものを下図に示します。
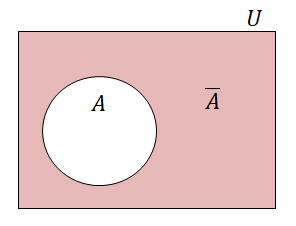
\(\overline{A}\)の定義は次の通りです。
補集合には以下の簡単な性質があります。 ベン図で確認してみてください。
- \(A \cap \overline{A} = \varnothing\)
- \(A \cup \overline{A} = U\)
- \(\overline{\overline{A}} = A\)
- \(A \subset B\)のとき\(\overline{B} \subset \overline{A}\)
3つ目の左辺は「\(A\)の補集合」の補集合です。 4つ目はイメージしづらいかもしれませんね。 \(A \subset B\)のときの\(\overline{A}, \overline{B}\)を下のベン図に示すので確認してみてください。
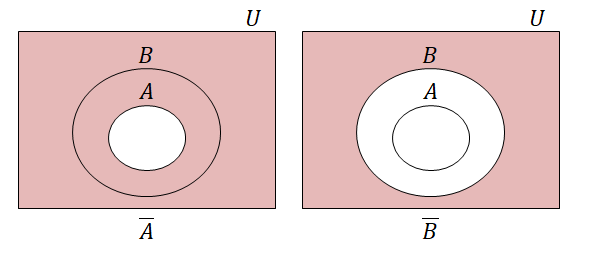
もうひとつ補集合に関する重要な法則として,次のド・モルガンの法則があります。
- \(\overline{A \cap B} = \overline{A} \cup \overline{B}\)
- \(\overline{A \cup B} = \overline{A} \cap \overline{B}\)
これもベン図で確認しましょう。 1つ目の式の左辺を下図に示します。 \(\overline{A \cap B}\)は\(A \cap B\)でない部分ですね。

右辺は下図のようになります。 \(\overline{A}\)と\(\overline{B}\)の領域をよく見て,\(\overline{A} \cup \overline{B}\)がどうなるか確認してください。
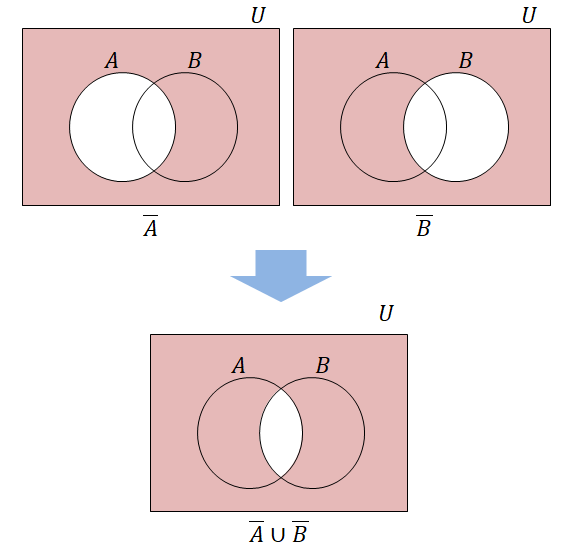
こうしてベン図で表すと\(\overline{A \cap B} = \overline{A} \cup \overline{B}\)となることが分かりますね。 \(\overline{A \cup B} = \overline{A} \cap \overline{B}\)についてもベン図を描いて確認してみてください。
確認問題
集合\(\{0, 2, 4\}\)の部分集合をすべて答えてください。
答え
要素の数が少ないものから順に考えてみましょう。 要素の数は\(0\)個から\(3\)個までありえます。 よって,部分集合は\(\varnothing\), \(\{0\}\),\(\{2\}\),\(\{4\}\), \(\{0, 2\}\),\(\{2, 4\}\),\(\{0, 4\}\), \(\{0, 2, 4\}\)です。 空集合\(\varnothing\)や元の集合\(\{0, 2, 4\}\)そのものも部分集合になるので注意してください。
ちなみに,部分集合の個数は計算で求めることができます。 数学Aで学ぶ「場合の数」の考え方を使いますが,各要素を部分集合に含めるかどうかで考えれば良いです。 \(3\)個の要素それぞれについて,部分集合に含めるか否かの\(2\)通りがあるので,部分集合の個数は\(2^3 = 8\)個です。
次の集合\(A, B\)に包含関係はあるでしょうか? 包含関係がある場合,\(A \subset B, A \supset B, A = B\)のどれでしょうか? 全体集合は実数全体とします。
-
\( \begin{eqnarray} \left\{ \begin{array}{l} A = \{1, 2, 3, 4\} \\ B = \{1, 3, 5, 7\} \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} A = \{x \ \vert \ 1 < x \leqq 5\} \\ B = \{x \ \vert \ 3 \leqq x < 5\} \end{array} \right. \end{eqnarray} \)
答え
-
ベン図を描いて,図内に要素を書き込んでみると下図のようになります。
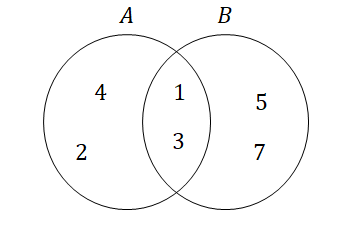
この図から\(A \subset B\)にも\(A \supset B\)にもなっておらず,\(A, B\)間に包含関係がないことが分かります。
部分集合の定義に沿って確かめると,\(2 \in A\)なのに\(2 \notin B\)なので\(A \subset B\)ではなく, \(5 \in B\)なのに\(5 \notin A\)なので\(A \supset B\)ではありません。 したがって\(A, B\)間に包含関係はないということになります。
-
全体集合を実数全体としたので,\(1 < x \leqq 5\)や\(3 \leqq x < 5\)を満たす\(x\)は無数にあり,\(A, B\)は無限集合です。 なので(1)のようにベン図に要素をすべて書き込んで確かめることはできません。
実数の範囲を表すツールとして数直線がありましたね。 これを活用すると,\(A, B\)を下図のように表せます。
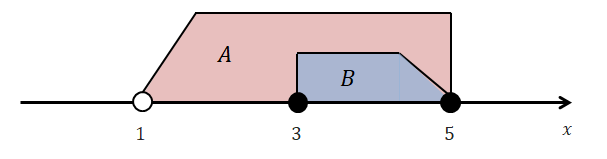
この図から,\(A \supset B\)という包含関係があることが分かります。
部分集合の定義に沿って確かめると,\(2 \in A\)なのに\(2 \notin B\)なので\(A \subset B\)ではありません。 また,\(B\)の要素\(x\)はすべて\(3 \leqq x < 5\)を満たすから,\(1 < 3 \leqq x < 5 \leqq 5\)より\(A\)の条件も満たし,\(x \in A\)でもあります。 したがって,\(A \supset B\)であることが分かります。
ベン図をかくと視覚的に分かりやすいですが,問題によってはベン図をかくのが難しい場合もあります。 部分集合の定義に沿った説明もできるようにしておきましょう。
\(U = \{1, 3, 5, 7, 9, 11\}\)を全体集合とします。 \(U\)の部分集合\(A = \{3, 9\}\)と\(B = \{3, 5, 7, 11\}\)を考えます。 このとき,次の集合を求めてください。
-
\(\overline{A}\)
-
\(\overline{A \cap B}\)
-
\(\overline{A} \cap B\)
-
\(A \cup \overline{B}\)
答え
\(U, A, B\)をベン図に表すと次のようになります。 問題の各集合がベン図の中でどの部分にあたるのか考えましょう。
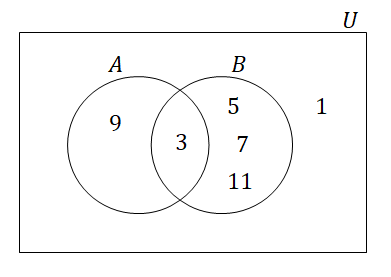
-
\(\overline{A}\)は下図の領域です。
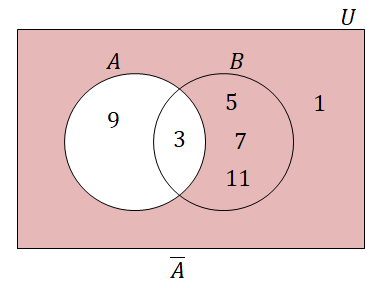
図より\(\overline{A} = \{1, 5, 7, 11\}\)です。
-
\(\overline{A \cap B}\)は下図の領域です。
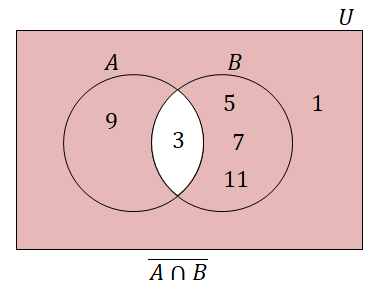
図より\(\overline{A \cap B} = \{1, 5, 7, 9, 11\}\)です。
-
\(\overline{A} \cap B\)は下図の領域です。
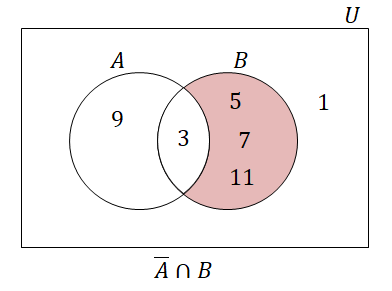
図より\(\overline{A} \cap B = \{5, 7, 11\}\)です。
-
\(A \cup \overline{B}\)は下図の領域です。
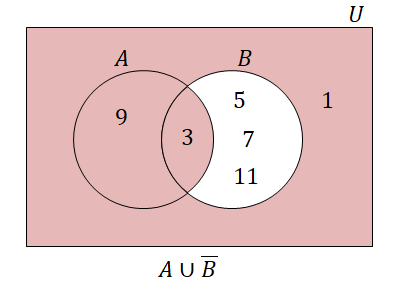
図より\(A \cup \overline{B} = \{1, 3, 9\}\)です。 ド・モルガンの法則より\(A \cup \overline{B} = \overline{\overline{A} \cap B}\)なので,(3)の結果を利用することもできますね。
