今回は集合について説明していきます。 「どんな範囲で物事を考えるか」を意識することは重要で,数学の理解には欠かせません。 集合はそんな「特定の範囲」を表すものです。
目次
集合と要素
範囲がはっきりとしたものの集まりを集合といい,集合を構成する1つ1つのものをその集合の要素といいます。 要素のことを元と呼ぶこともあります。
\(x\)が集合\(A\)の要素であるとき,\(x\)は\(A\)に属するといい,\(x \in A\)と表します。 また\(x\)が集合\(A\)の要素でないとき,\(x\)は\(A\)に属さないといい,\(x \notin A\)と表します。 どちらも\(A \ni x\)のように逆向きに並べても構いません。
ちなみに\(\in\)という記号に決まった読み方はなく,\(x \in A\)は単に「\(x\)は\(A\)に属する」などと読みます。
集合は「範囲がはっきりしている」といいましたが,どういう意味でしょうか。 それは,どんなものでもその集合に属するか属さないか明確に定まるということです。 例えば「すべての実数を集めたもの」は集合です。 これを\(\mathbb{R}\)と表すと,どんなものに対しても「\(5 \in \mathbb{R}\)」や「猫\(\notin \mathbb{R}\)」など明確に定まります。
集合にならないものの例としては「大きな数の集まり」があります。 これを\(A\)と表すと,例えば\(1000\)は\(A\)に属するでしょうか? \(1000\)が大きいかどうかは人によって,場合によって変わりますよね。 このように\(A\)は,どんなものに対しても\(A\)に属するかどうかを明確に定められないので,集合ではありません。
有限個の要素からなる集合を有限集合,無限個の要素からなる集合を無限集合といいます。 「\(5\)以下の自然数全体の集合」は有限集合,「\(5\)以下の実数全体の集合」は無限集合ですね。
集合の表し方
続いて集合の表し方を説明します。 集合は要素の集まりですから,要素をすべて列挙することで集合を表せます。 「\(5\)以下の自然数全体の集合」を\(A\)とすると,\(A\)は次のように表せます。
このように有限集合は\(\{ \}\)の中に要素を列挙することで表せます。
しかし無限集合の場合は要素を列挙できませんし,有限集合であっても要素が多いときはいちいち全部書きたくないです。 そこで要素が多い集合については,要素が満たす条件を書くことで集合を表します。 「\(5\)以下の実数全体の集合」を\(B\)とすると,\(B\)は次のように表せます。
このように\(\vert\)の左側に要素の形を,右側に要素の条件を書くことで集合を表せます。 条件が複数あるときは,この例のようにコンマで区切って列挙します。
また,要素の並びに明らかな規則性があるときは,「\(\cdots\)」を使って要素の記述を省略できます。 「正の偶数全体の集合」を\(C\)とすると,\(C\)は次のように表せます。
もちろん,要素の条件を使って次のように表すこともできます。
こんな風に集合は色んな方法で表せるんですね。
共通部分と和集合
複数の集合について考えるとき,それらを図示すると関係性が分かりやすいです。 集合は下図のように図示できて,このような図をベン図といいます。 集合を円で表して,「この円の範囲内は集合\(A\)ですよ~」という具合に表すわけです。
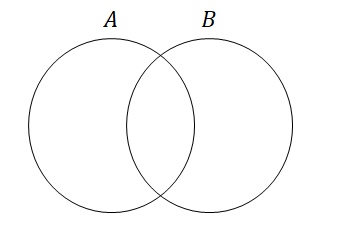
2つの集合を考える場合,上図のようにそれらが重なる部分があるかもしれません。 これをそれらの集合の共通部分といいます。 共通部分に色をつけてみると下図のようになります。
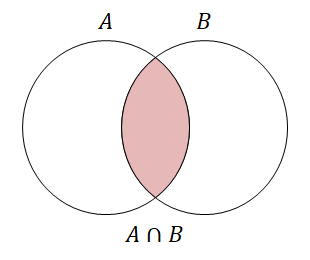
図中にも書きましたが,集合の共通部分は\(\cap\)という記号を使って表します。 集合\(A, B\)の共通部分であれば\(A \cap B\)と表し,「\(A\)かつ\(B\)」や「\(A\)キャップ\(B\)」と読みます。 もう少しちゃんと書くと,\(A \cap B\)は次の集合のことです。
上では2つの集合の共通部分を考えましたが,今度は2つの集合をすべてあわせた集合を考えましょう。 これをそれらの集合の和集合といいます。 和集合に色をつけてみると下図のようになります。
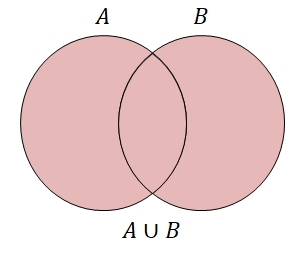
和集合は\(\cup\)という記号を使って表します。 集合\(A, B\)の和集合であれば\(A \cup B\)と表し,「\(A\)または\(B\)」や「\(A\)カップ\(B\)」と読みます。 もう少しちゃんと書くと,\(A \cup B\)は次の集合のことです。
日常語で「\(A\)または\(B\)」や「\(A\)か\(B\)」というと,\(A, B\)のどちらか一方という意味になることが多いです。 しかし,数学の「または」は\(A, B\)両方の場合を含みます。
両方を含む「または」を論理和といいますが,片方だけを選ぶ「または」は排他的論理和といいます。 日常語の「または」は排他的論理和であることが多いようですが,\(A \cup B\)の「または」は論理和なのです。
\(\cap\)と\(\cup\)・・・慣れないうちはややこしい記号だと思います。 そこで,いくつか記憶の手掛かりになるものを紹介しようと思います。
まずは記号の由来を紹介します。 和集合を英語で union といいますが,和集合の記号\(\cup\)は, union の頭文字からきています。 union という英単語には,結合や連合の意味合いがあり,和集合のイメージと合っていますね。
共通部分と和集合はペアで考えられる概念です。 そこで,共通部分の記号については,和集合の\(\cup\)をひっくり返して\(\cap\)となります。
次に記号の形を手掛かりにしてみます。 \(\cap\)をよく見ると,指先でつまむような形に見えませんか? 集合の共通要素だけを選んでつまみとるイメージを持つと,この記号が共通部分を表すものだと連想できます。
次に\(\cup\)ですが,両掌を広げたような形に見えませんか? 広げた掌で集合のすべての要素をすくい上げるイメージを持つと,この記号が和集合を表すものだと連想できます。
漢字を使った覚え方もあります。 「かつ」は「且つ」と書きますが,この漢字,\(\cap\)っぽい形をしてますよね。 「または」は「又は」と書きますが・・・交差してる部分がちょっとだけ\(\cup\)っぽい形をしてるような・・・?
\(\cap, \cup\)について,次の交換法則・結合法則が成り立ちます。
-
交換法則
\(\quad A \cap B = B \cap A\)
\(\quad A \cup B = B \cup A\) -
結合法則
\(\quad (A \cap B) \cap C = A \cap (B \cap C)\)
\(\quad (A \cup B) \cup C = A \cup (B \cup C)\)
交換法則が成り立つのは当たり前ですね。 結合法則では3つの集合が登場していますが,どんな順番で共通部分や和集合を考えても結果は同じということです。
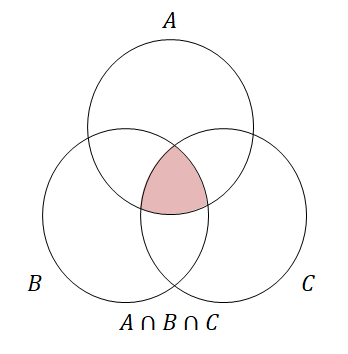
なのでわざわざ\(()\)をつけて共通部分や和集合をとる順番を明確にする必要はありません。 共通部分は単に\(A \cap B \cap C\),和集合は単に\(A \cup B \cup C\)と表しても問題ないわけです。 これらを図示すると,下図のようになります。
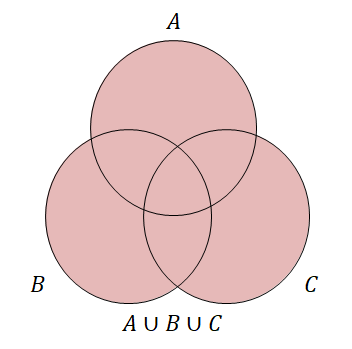
\(A \cap B \cap C, A \cup B \cup C\)をちゃんと書くと次の集合のことですね。
\( = \{x \ \vert \ x \in A \) かつ \( x \in B \) かつ \( x \in C \} \)
\( = \{x \ \vert \ x \in A \) または \( x \in B \) または \( x \in C \} \)
3つの集合の共通部分などを考えるときは,上のようなベン図をかきます。 このようにかくと,\(A\),\(B\),\(C\),\(A \cap B\),\(B \cap C\),\(C \cap A\)、\(A \cap B \cap C\)のすべてが登場するので,集合の重なり合いを考えるのに便利です。
ちなみに集合が4つ以上になると,綺麗に重なり合うベン図をかくことが難しくなります。 この場合,円では表せないので楕円を使うのですが,まず使う機会はないでしょう。
確認問題
以下に示すものは集合といえるでしょうか? それぞれ答えてください。
-
小さな数全体の集まり
-
素数全体の集まり
-
絶対値が\(3\)未満の実数全体の集まり
-
英数字からなる文字列全体の集まり
答え
-
集合とはいえません。 ある数が小さいかどうか,明確な判断基準はありません。
-
集合といえます。 数でないものはこの集まりには属しませんし,ある数が素数かどうかは明確に判断できます。
-
集合といえます。 実数でないものはこの集まりには属しませんし,ある実数の絶対値が\(3\)未満かどうかは明確に判断できます。
-
集合といえます。 文字列でないものはこの集まりには属しませんし,ある文字列が英数字からなるかどうかは明確に判断できます。
次のように集合\(A, B\)を定めるとき,\(A \cap B\)と\(A \cup B\)がどんな集合になるか答えてください。 ただし,\(\mathbb{Z}\)を整数全体の集合とします。
-
\( \begin{eqnarray} \left\{ \begin{array}{l} A = \{1, 2, 3\} \\[5pt] B = \{2, 3, 4\} \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} A = \{2x \ \vert \ x \in \mathbb{Z}\} \\[5pt] B = \{4x \ \vert \ x \in \mathbb{Z}\} \end{array} \right. \end{eqnarray} \)
答え
\(A \cap B\)は\(A\)と\(B\)に共通する要素全体の集合です。 \(A \cup B\)は\(A\)か\(B\)に存在する要素全体の集合です。
-
\(A \cap B = \{2, 3\}\)で,\(A \cup B = \{1, 2, 3, 4\}\)です。
-
\(A\)は\(2\)の倍数全体の集合,\(B\)は\(4\)の倍数全体の集合です。 なので\(A\)と\(B\)に共通する要素は\(4\)の倍数であり,\(A \cap B = \{4x \ \vert \ x \in \mathbb{Z}\}\)です。 また\(A\)か\(B\)に存在する要素はすべて\(2\)の倍数であり,\(A \cup B = \{2x \ \vert \ x \in \mathbb{Z}\}\)です。
次の集合\(A, B, C\)に対して,\(A \cap B \cap C\)と\(A \cup B \cup C\)を求めてください。
答え
\(A \cap B \cap C\)は\(A, B, C\)すべてに存在する要素を集めた集合です。 \(A \cup B \cup C\)は\(A, B, C\)に存在する要素をすべて集めた集合です。 なので\(A \cap B \cap C = \{3, 7\}\)で,\(A \cup B \cup C = \{1, 2, 3, 5, 7, 9, 11\}\)です。
