文字定数を含む問題を扱ってみましょう。 定数などの意味合いがピンと来ない方はこちらにどうぞ。
目次
係数でない文字定数
係数でない文字定数の扱いを練習しましょう。 \(a\)を定数とする次の連立不等式を解きます。
この不等式を数直線を用いて表すと\(a\)の値によって次の2つが考えられます。
(1) \(5 < a\)の場合
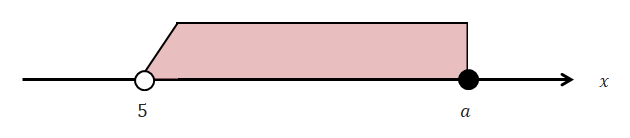
(2) \(a \leqq 5\)の場合

上の図を見ると\(a\)の値によって不等式の解が変わることが分かります。 不等式の解は\(5 < a\)のとき「\(5 < x \leqq a\)」で\(a \leqq 5\)のとき「解なし」です。
このように文字定数を含む問題を考えるときには場合分けが必要かもしれません。 特に不等式の場合には,数の大小が問題となるので場合分けが重要になります。 この例では\(5\)と\(a\)の大小関係によって場合分けが必要でしたね。
ちなみに上の場合分けでは\(5 < a\)と\(a \leqq 5\)の2つに分けましたが, 2つの場合の境目である\(a = 5\)をどちらの場合に入れるべきかには十分注意してください。 この例ではちょうど\(a = 5\)の場合は解なしになるので上のような場合分けになりました。 \(5 \leqq a\)と\(a < 5\)の2つに場合分けすることはできません。
文字係数
次は文字定数が係数になっている問題を考えましょう。 \(5x = 10\)という方程式を解くとき両辺を\(x\)の係数である\(5\)で割りますよね。 このように「係数で割る」という計算をよく行います。 割り算を行う際にはいくつか注意点がありますのでまずはそれを確認しましょう。
文字係数を含む不等式を解くときには次の点に注意してください。
(1) \(0\)で割ってはいけない。
(2) 両辺を負の数で割ると不等号の向きが反転する。
\(0\)で割るという計算は定義されていません。 そのような計算はそもそも存在しないわけです。
\(0\)で割るというのは\(0\)の逆数を掛けるということです。 \(0\)の逆数とは\(0\)にかけて\(1\)になる数のことです。 しかし\(0\)にどんな実数を掛けても\(0\)になってしまいます。 つまり\(0\)の逆数は存在せず,逆数が存在しないので割り算もできないのです。
これを踏まえて次のシンプルな不等式を解いてみましょう。 \(a\)を定数とします。
こんな式を見たらとりあえず両辺を\(a\)で割りたくなります。 でもちょっと待ってください。もし\(a = 0\)だったら\(0\)で割ることになってまずいです。 両辺を\(a\)で割れるのは\(a \neq\ 0\)のときだけです。 これでまず\(a = 0\)と\(a \neq 0\)の2つの場合分けが必要です。
\(a = 0\)のとき不等式は\(0 < 1\)となります。もはや\(x\)が残っていませんね。 そして\(0 < 1\)というのは正しい不等式です。 つまりこの不等式は\(x\)がどんな値であろうとも正しいわけです。 というわけでこのときの不等式の解は「すべての実数」です。
次に\(a \neq 0\)の場合を考えましょう。このときは両辺を\(a\)で割ることができます。 しかしまだ気を付けるべきことがあります。それは\(a\)の符号です。 \(a\)がマイナスの場合,両辺を\(a\)で割ると不等号の向きが反転します。 つまり\(a > 0\)と\(a < 0\)の2つの場合分けがさらに必要です。
\(a > 0\)のとき両辺を\(a\)で割って,不等式の解は\(x < \displaystyle\frac{1}{a}\)です。 \(a < 0\)のときは不等号の向きが反転するので不等式の解は\(x > \displaystyle\frac{1}{a}\)です。
以上をまとめると\(ax < 1\)というシンプルな不等式にも3つの場合分けが必要で, 解は\(a \neq 0\)のときすべての実数,\(a > 0\)のとき\(x < \displaystyle\frac{1}{a}\),\(a < 0\)のとき\(x > \displaystyle\frac{1}{a}\)です。
確認問題
\(a\)を定数とします。 次の連立不等式を解いてください。
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x > 1 \\ x > a \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x > 1 \\ x \geqq a \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x \geqq 1 \\ x > a \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x \geqq 1 \\ x \geqq a \end{array} \right. \end{eqnarray} \)
答え
どの問題も\(1\)と\(a\)の大小関係で場合分けが必要ですね。 また\(a = 1\)になる場合も要注意です。 自分で数直線を描きながら確認しましょう。
-
\(a < 1\)の場合,解は\(x > 1\)です。
\(a \geqq 1\)の場合,解は\(x > a\)です。
\(a = 1\)の\(=\)はどちらの場合に入れてもOKです。(\(a \leqq 1\)と\(a > 1\)の場合分けでもOK) -
\(a \leqq 1\)の場合,解は\(x > 1\)です。
\(a > 1\)の場合,解は\(x \geqq a\)です。
\(a = 1\)の場合の解は\(x > 1\)になるので,この場合分けになります。 -
\(a < 1\)の場合,解は\(x \geqq 1\)です。
\(a \geqq 1\)の場合,解は\(x > a\)です。
\(a = 1\)の場合の解は\(x > a\)になるので,この場合分けになります。 -
\(a < 1\)の場合,解は\(x \geqq 1\)です。
\(a \geqq 1\)の場合,解は\(x \geqq a\)です。
\(a = 1\)の\(=\)はどちらの場合に入れてもOKです。(\(a \leqq 1\)と\(a > 1\)の場合分けでもOK)
\(a\)を定数とします。 次の連立不等式を解いてください。
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x < 1 \\ x > a \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x < 1 \\ x \geqq a \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x \leqq 1 \\ x > a \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x \leqq 1 \\ x \geqq a \end{array} \right. \end{eqnarray} \)
答え
どの問題も\(1\)と\(a\)の大小関係で場合分けが必要ですね。 また\(a = 1\)になる場合も要注意です。 自分で数直線を描きながら確認しましょう。
-
\(a < 1\)の場合,解は\(a < x < 1\)です。
\(a \geqq 1\)の場合,解なしです。
\(a = 1\)の場合は解なしになるので,この場合分けになります。 -
\(a < 1\)の場合,解は\(a \leqq x < 1\)です。
\(a \geqq 1\)の場合,解なしです。
\(a = 1\)の場合は解なしになるので,この場合分けになります。 -
\(a < 1\)の場合,解は\(a < x \leqq 1\)です。
\(a \geqq 1\)の場合,解なしです。
\(a = 1\)の場合は解なしになるので,この場合分けになります。 -
\(a < 1\)の場合,解は\(a \leqq x \leqq 1\)です。
\(a > 1\)の場合,解なしです。
\(a = 1\)の場合,解は\(x = 1\)です。(この場合2つの不等式の範囲が\(x = 1\)の1点で交わります。)
\(a\)を定数とします。 次の不等式を解いてください。
答え
両辺を\(a\)で割りたくなる見た目をした不等式ですね。 \(0\)割りや不等号の反転に気を付けましょう。
[1] \(a = 0\)の場合
不等式は\(0 < 0\)という式になります。
この不等式は\(x\)の値に関わらず正しくないので,このとき解なしです。
(\(0 \leqq 0\)なら正しいですが\(0 < 0\)は正しくないですね。)
[2] \(a > 0\)の場合
\(a \neq 0\)なので両辺を\(a\)で割ると,解は\(x < 1\)
[3] \(a < 0\)の場合
\(a \neq 0\)なので両辺を\(a\)で割ると,解は\(x > 1\)
\(a\)が負なので不等号の向きが反転したことに注意です。
