絶対値を含む不等式に挑戦してみましょう。 場合分けの練習にもなります。
目次
場合分けしない問題
まずは場合分けの必要がない問題を扱います。 絶対値を機械的にはずせる問題です。
不等式の前に次の方程式を考えてみましょう。
絶対値が\(2\)になるということは\(x - 1\)の値は\(2\)か\(-2\)ですね。 なので上の方程式は\(x - 1 = 2\)または\(x - 1 = -2\)と分解されます。 それぞれ解くと,この方程式の解が\(x = 3, -1\)であることが分かります。
このように「絶対値がこの値になるのはどんなとき?」を考えれば絶対値をはずせます。
次は不等式の例を見てみましょう。 絶対値が原点からの距離であることを意識してください。
絶対値が\(2\)未満なのは数直線では下図の範囲です。 原点からの距離が\(2\)未満の範囲ですね。

図より\(\vert x - 1 \vert < 2\)の絶対値をはずすと\(-2 < x - 1 < 2\)となると分かります。 なのでこの不等式の解は\(-1 < x < 3\)となります。
もうひとつ例を見てみましょう。 さっきの不等式の不等号の向きを変えてみます。
絶対値が\(2\)より大きくなるのは下図の範囲です。 原点からの距離が\(2\)よりも大きい範囲ですね。

図より\(\vert x - 1 \vert > 2\)の絶対値をはずすと\(x - 1 < -2, \ 2 < x - 1\)となると分かります。 なのでこの不等式の解は\(x < -1, \ 3 < x\)となります。
不等式の解で\(x > 3\)ではなく\(3 < x\)と書きました。 これは直前の\(x < -1\)と不等号の向きをそろえるためです。 このようにいくつかの不等式を並べる場合は不等号の向きをそろえることが多いです。
場合分けする問題
さっきまでの問題は図にしてみれば簡単に不等号をはずせました。 今度は場合分けが必要な問題を解いてみましょう。
まずは次の不等式を解いてみましょう。
これは右辺にも\(x\)がありますね。こうなるとさっきほど単純にはいきません。 例えば\(0 \leqq \vert x + 1 \vert\)であることから\(0 < 2x + 5\)という隠れた条件があったりします。
こういう問題は次の絶対値の性質を使って絶対値をはずすようにしましょう。
\(a \geqq 0\)のとき\(\vert a \vert = a\)
\(a < 0\)のとき\(\vert a \vert = -a\)
絶対値の中身の符号に応じて場合分けして絶対値をはずすわけです。 改めて不等式\(\vert x + 1 \vert < 2x + 5\)を考えてみましょう。
\(x + 1 \geqq 0\)すなわち\(x \geqq -1\)のとき\(\vert x + 1 \vert = x + 1\)で, \(x + 1 < 0\)すなわち\(x < -1\)のとき\(\vert x + 1 \vert = -(x + 1) = -x - 1\)です。
これで上の不等式の絶対値が,次のような場合分けではずせることが分かりました。
(1) \(x \geqq -1\)のとき\(x + 1 < 2x + 5\)
(2) \(x < -1\)のとき\(-x - 1 < 2x + 5\)
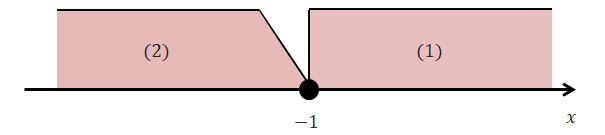
まず(1)を考えましょう。不等式を解くと\(x > -4\)ですね。 これは\(x \geqq -1\)の範囲内での解が\(x > -4\)ということです。 なのでこれらの共通部分を考えなくてはなりません。 下図を見ると(1)の解が\(x \geqq -1\)であることが分かります。

次は(2)を考えましょう。不等式を解くと\(x > -2\)です。 これは\(x < -1\)の範囲内での解が\(x > -2\)ということです。 なのでこれらの共通部分を考えなくてはなりません。 下図を見ると(2)の解が\(-2 < x < -1\)であることが分かります。
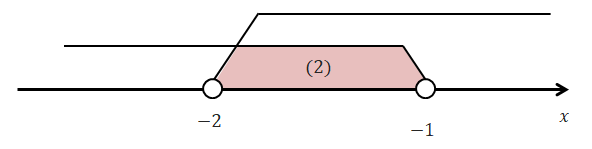
ここまで\(x \geqq -1\)の場合と\(x < -1\)の場合を別々に考えました。 最後はちゃんと解を統合しましょう。 (1)と(2)の解を合わせて図示すると下図のようになります
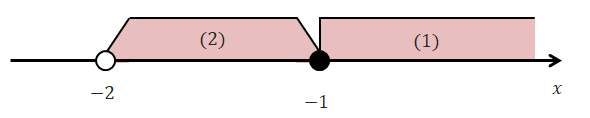
これで2つの解が\(x = -1\)で繋がって最終的な解は\(x > -2\)になることが分かりました。 絶対値を含む問題はこのような場合分けで解くことができます。
場合分けが必要な問題には,他にも2つの絶対値がある問題などがあります。 確認問題にもあるのでぜひ解いてみてください。
確認問題
次の不等式を解いてください。
-
\(\vert 2x \vert \leqq 10\)
-
\(\vert x - 5 \vert > 3\)
答え
-
場合分けが不要な不等式です。 絶対値をはずすと\(-10 \leqq 2x \leqq 10\)です。 辺々\(\displaystyle\frac{1}{2}\)倍すると解が\(-5 \leqq x \leqq 5\)だと分かります。
-
場合分けが不要な不等式です。 絶対値をはずすと\(x - 5 < -3 , \ 3 < x - 5\)です。 辺々\(+5\)すると解が\(x < 2, \ 8 < x\)だと分かります。
次の不等式を解いてください。
-
\(\vert 2x + 1 \vert > x\)
-
\(\vert x - \vert 2x - 5 \vert\ \vert < 3\)
-
\(\vert 2x - 3 \vert - \vert x - 1 \vert < 5\)
答え
自分で数直線を用いた図を描きながら確認しましょう。
-
絶対値の中が正の場合と負の場合で場合分けします。
[1] \(2x + 1 \geqq 0\)すなわち\(x \geqq -\displaystyle\frac{1}{2}\)の場合を考えます。 このとき\(\vert 2x + 1 \vert = 2x + 1\)なので不等式は\(2x + 1 > x\)となります。 これを解くと\(x > -1\)となります。 これと\(x \geqq -\displaystyle\frac{1}{2}\)との共通部分をとると\(x \geqq -\displaystyle\frac{1}{2}\)がこの場合の解だと分かります。
[2] \(2x + 1 < 0\)すなわち\(x < -\displaystyle\frac{1}{2}\)の場合を考えます。 このとき\(\vert 2x + 1 \vert = -(2x + 1)\)なので不等式は\(-(2x + 1) > x\)となります。 これを解くと\(x < -\displaystyle\frac{1}{3}\)となります。 これと\(x < -\displaystyle\frac{1}{2}\)との共通部分をとると\(x < -\displaystyle\frac{1}{2}\)がこの場合の解だと分かります。
[1], [2]の解を合わせると,\(x\)が全ての範囲をとることが分かります。 したがって解はすべての実数です。
-
絶対値が2重になっていますが内側の絶対値からはずしましょう。
[1] \(2x - 5 \geqq 0\)すなわち\(x \geqq \displaystyle\frac{5}{2}\)の場合を考えます。 このとき\(\vert 2x - 5 \vert = 2x - 5\)なので不等式は\(\vert x - (2x - 5) \vert < 3\)となります。 整理すると\(\vert x - 5 \vert < 3\)です。(\(\vert -a \vert = \vert a \vert\)という形の式変形をしました。) この絶対値は\(-3 < x - 5 < 3\)と簡単に外せますね。これを解くと\(2 < x < 8\)です。 これと\(x \geqq \displaystyle\frac{5}{2}\)との共通部分をとると\(\displaystyle\frac{5}{2} \leqq x < 8\)がこの場合の解だと分かります。
[2] \(2x - 5 < 0\)すなわち\(x < \displaystyle\frac{5}{2}\)の場合を考えます。 このとき\(\vert 2x - 5 \vert = -(2x - 5)\)なので不等式は\(\vert x + (2x - 5) \vert < 3\)となります。 整理すると\(\vert 3x - 5 \vert < 3\)です。 この絶対値は\(-3 < 3x - 5 < 3\)と簡単に外せますね。これを解くと\(\displaystyle\frac{2}{3} < x < \displaystyle\frac{8}{3}\)です。 これと\(x < \displaystyle\frac{5}{2}\)との共通部分をとると\(\displaystyle\frac{2}{3} < x < \displaystyle\frac{5}{2}\)がこの場合の解だと分かります。
[1], [2]の解を合わせると\(x = \displaystyle\frac{5}{2}\)で両者の範囲が繋がりますね。 その結果,解は\(\displaystyle\frac{2}{3} < x < 8\)となります。
-
絶対値が2つあるので何パターンか場合分けが必要です。 絶対値の中が\(0\)になる\(x\)の前後で絶対値の中の正負が切り替わります。 つまり\(\displaystyle\frac{3}{2}\)と\(1\)の前後で絶対値のはずれ方が変わります。 したがって\(\ x < 1\ \)と\(\ 1 \leqq x < \displaystyle\frac{3}{2}\ \)と\(\ \displaystyle\frac{3}{2} \leqq x\ \)の場合分けが必要です。
[1] \(x < 1\)の場合を考えます。 このとき\(\vert 2x - 3 \vert = -(2x - 3)\),\(\vert x - 1 \vert = -(x - 1)\)となります。 よって不等式は\(-(2x - 3) + (x - 1) < 5\)となり,これを解くと\(x > -3\)です。 これと\(x < 1\)との共通部分をとると\(-3 < x < 1\)がこの場合の解だと分かります。
[2] \(1 \leqq x < \displaystyle\frac{3}{2}\)の場合を考えます。 このとき\(\vert 2x - 3 \vert = -(2x - 3)\),\(\vert x - 1 \vert = x - 1\)となります。 よって不等式は\(-(2x - 3) - (x - 1) < 5\)となり,これを解くと\(x > -\displaystyle\frac{1}{3}\)です。 これと\(1 \leqq x < \displaystyle\frac{3}{2}\)との共通部分をとると\(1 \leqq x < \displaystyle\frac{3}{2}\)がこの場合の解だと分かります。
[3] \(\displaystyle\frac{3}{2} \leqq x\)の場合を考えます。 このとき\(\vert 2x - 3 \vert = 2x - 3\),\(\vert x - 1 \vert = x - 1\)となります。 よって不等式は\(2x - 3 - (x - 1) < 5\)となり,これを解くと\(x < 7\)です。 これと\(\displaystyle\frac{3}{2} \leqq x\)との共通部分をとると\(\displaystyle\frac{3}{2} \leqq x < 7\)がこの場合の解だと分かります。
[1], [2], [3]の解を合わせると\(x = 1, \displaystyle\frac{3}{2}\)で\(x\)の範囲が繋がりますね。 その結果,解は\(-3 < x < 7\)となります。
