大小関係を比較するということは日常でもよく行います。 価格の大小,報酬の大小,苦痛の大小などいろいろ比較しながら生きています。 不等式は単純な大小比較のみならず「どんな時こっちの方が大きくなるかな」なども考えます。
目次
不等式
不等式は数や式の大小関係を不等号で表した式です。 左辺,右辺など不等式の用語は等式の場合と同じです。
今までも何度も使ってきた不等号ですが,改めてその意味を確認しておきます。
| 不等号 | 意味 |
|---|---|
| \(a \lt b\) |
\(a\)は\(b\)よりも小さい (\(a\)は\(b\)未満) \(a = b\)の場合を含みません。 |
| \(a \leqq b\) |
\(a\)は\(b\)以下 \(a = b\)の場合を含みます。 |
| \(a \gt b\) |
\(a\)は\(b\)よりも大きい \(a = b\)の場合を含みません。 |
| \(a \geqq b\) |
\(a\)は\(b\)以上 \(a = b\)の場合を含みます。 |
下側に\(=\)のついた不等号は両辺が等しい場合も含みます。 下側に\(=\)のつかない不等号は両辺が等しい場合は含みません。
次に不等式の性質を確認しましょう。
-
推移律
\( \begin{align} a < b, \ b < c \ \ \ \ \ \Rightarrow \ \ \ \ \ a < c \end{align} \)
-
両辺に加算
\( \begin{align} a < b \ \ \ \ \ \Rightarrow \ \ \ \ \ a + c < b + c \end{align} \)
-
両辺に乗算
\( \begin{align} a < b, \ c > 0 \ \ \ \ \ \Rightarrow \ \ \ \ \ ac < bc \\[5pt] a < b, \ c < 0 \ \ \ \ \ \Rightarrow \ \ \ \ \ ac > bc \end{align} \)
せっかくなので数直線を使いながら順に確認してみましょう。
まず1つ目ですが,\(a < b, \ b < c\)という大小関係を数直線上に表すと下図のようになります。 右側ほど大きいのでこの順番に\(a, b, c\)が並びます。 このとき\(a\)よりも右に\(c\)があるので\(a < c\)であることが分かりますね。
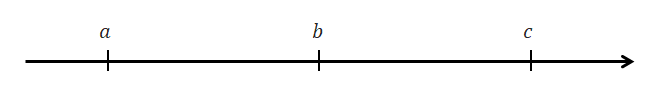
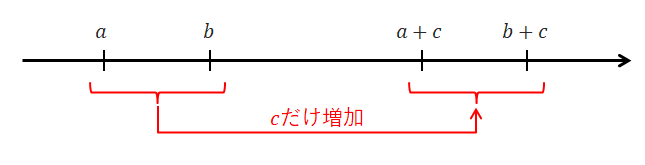
次に2つ目ですが,両辺に同じ数を足しても大小関係は変わらないという内容です。 両辺に\(c\)を足すことで両辺とも数直線上を右側に\(c\)だけスライドします。 このとき\(a + c, \ b + c\)の大小関係は\(a, b\)のときと同じであることが分かりますね。 「増加」ではなく「減少」する場合も同様です。自分で数直線を書いてみましょう。
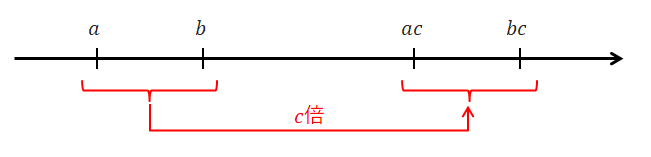
最後に3つ目ですが,両辺に同じ数をかけるとどうなるかという内容です。 正の数をかけても大小関係は変わりませんが,負の数をかけた場合は変わります。
まず正の数をかけた場合を考えてみましょう。 この場合,単純に\(a, b\)の原点からの距離が\(c\)倍されます。 原点からの距離が変わるだけで大小関係が変わることはありません。
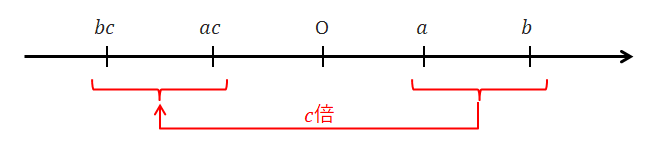
次に負の数をかけた場合を考えてみましょう。 この場合\(a, b\)はともに原点の反対側に移動します。 このとき右側にあった\(b\)が左側に,左側にあった\(a\)が右側に位置することになります。 負の数をかけたときは大小関係が変わるわけですね。
イメージしづらい性質があったら実際に適当な数を当てはめて試しましょう。
簡単な1次不等式
不等式の性質を使って簡単な1次不等式を解いてみましょう。
まずは\(3x + 5 > 20\)という不等式を解いてみます。 まず両辺に\(-5\)を足すと\(3x > 15\)になります。 次に両辺に\(\displaystyle\frac{1}{3}\)をかけると\(x > 5\)になり,これがこの不等式の解です。
左辺に\(x\)だけが残るように式変形していくわけですね。
次は\(10 - 2x \leqq 4\)という不等式を解いてみます。 まず両辺に\(-10\)を足すと\(-2x \leqq -6\)になります。 次に両辺に\(-\displaystyle\frac{1}{2}\)をかけると\(x \geqq 3\)になり,これがこの不等式の解です。 負の数を両辺にかけると不等号の向きが変わることに注意です。
不等式と数直線
不等式の解を数直線を用いてどう表すかを学んでおきましょう。 今後何度も使うことになります。
実際に見てみましょう。 次の図は\(x > 1\)を数直線を用いて表したものです。
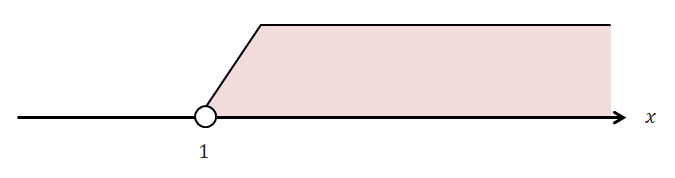
\(x > 1\)は\(x\)は\(1\)よりも大きいという意味ですね。 なので数直線の\(1\)より大きい所に色を塗って表します。 \(x\)についての不等式ということは数直線の矢先に\(x\)と書いて表します。
またこのような\(=\)を含まない不等式の場合は値を白丸で表します。 さらに白丸の真上の線は斜めに描いておきます。
ちなみにこの図を手で描く場合はいちいち色を塗っていられません。 そこで手描きの場合は下図のように色塗り部分を斜線で表現します。
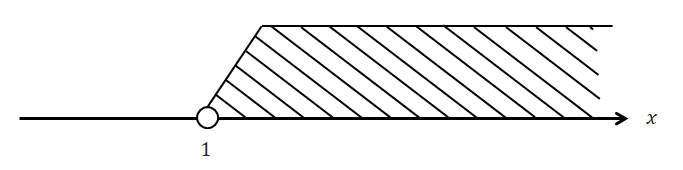
次に\(x \geqq 1\)を数直線を用いて表します。 次の図を見てください。

\(x > 1\)の図と似ていますが少し違います。 今度は値が黒丸で表されており,黒丸の真上の線はまっすぐに描かれています。 このようにして\(x > 1\)と\(x \geqq 1\)の図を区別できるようにしています。
次は反対向きの不等号も確認しましょう。 \(x < 1\)は下図のように表します。
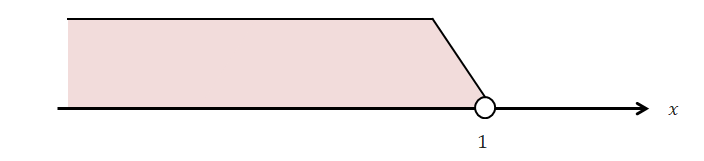
\(x > 1\)と基本的な描き方は同じですね。 今度は\(x\)が\(1\)より小さいことを表したいので\(1\)より小さい所に色を塗っています。
もうひとつの不等号も確認しておきましょう。 もうどんな図になるかは想像できますよね。 \(x \leqq 1\)は下図のように表します。
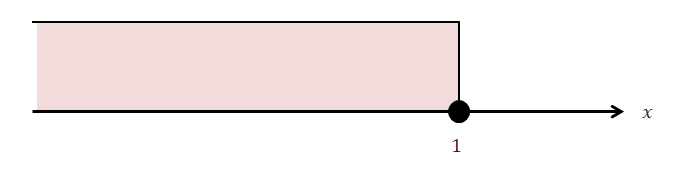
最後に\(3 \leqq x < 5\)という不等式を数直線を用いて表してみましょう。 これは下図のようになります。
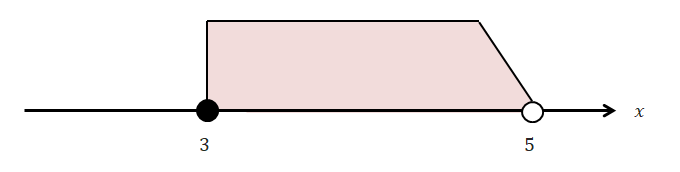
数直線上の\(3\)以上\(5\)未満の所に色が塗ってあります。 そして\(x\)は\(3\)になることはあっても\(5\)になることはないので,\(3\)は黒丸,\(5\)は白丸ですね。
連立不等式
簡単な不等式は解けるようになりました。 次はいくつかの不等式を組み合わせたものを解いてみましょう。 さっき学んだ数直線の表現ができれば簡単です。
例として次の連立不等式を解いてみましょう。
これは\(-2 < x \leqq 5\)と\(-4 \leqq x < 3\)の両方を満たす\(x\)の範囲は?という問題です。 式だけだと若干ややこしいですが,数直線を用いて表すと整理できます。 下図に数直線を用いた図を載せてあります。
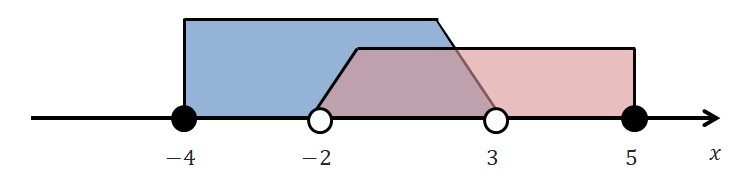
\(-2 < x \leqq 5\)を赤っぽい色,\(-4 \leqq x < 3\)を青っぽい色で表しました。 これらを両方満たす\(x\)の範囲とはこれらの領域が重なる範囲のことです。 図を描いてみればその範囲が\(-2 < x < 3\)であることがすぐ分かりますね。
連立不等式には次のような形もあります。
これは一見1つの不等式ですが,このまま解くことはできません。 このような不等式は左半分と右半分の2つに分けて連立して解きましょう。 つまり上の不等式は次の連立不等式に書き換えられます。
このような連立不等式の形もしばしば出てきます。 対応できるようにしておきましょう。
確認問題
次の\(x\)の候補のうち\(-1 < x \leqq 3\)を満たすものをすべて答えてください。
答え
不等号に\(=\)が付いているかどうか注意してください。 \(-1 < x \leqq 3\)は\(-1\)は含みませんが\(3\)は含みます。
次の不等式を解いてください。
-
\(x - 3 < 3\)
-
\(-5x \geqq 10\)
-
\(3x + 3 \leqq x - 9\)
-
\(-2x - 5 > 3x + 20\)
答え
-
両辺に\(+3\):\(x < 6\)
-
両辺に\(\times (-\displaystyle\frac{1}{5})\):\(x \leqq -2\)
負の数を両辺にかけると不等号の向きが変わることに注意です。
-
両辺に\(-x\):\(2x + 3 \leqq -9\)
両辺に\(-3\):\(2x \leqq -12\)
両辺に\(\times \displaystyle\frac{1}{2}\):\(x \leqq -6\) -
両辺に\(-3x\):\(-5x - 5 > 20\)
両辺に\(+5\):\(-5x > 25\)
両辺に\(\times (-\displaystyle\frac{1}{5})\):\(x < -5\)
次の連立不等式を解いてください。
-
\( \begin{eqnarray} \left\{ \begin{array}{l} 5 < x \leqq 12 \\ 8 < x \leqq 20 \end{array} \right. \end{eqnarray} \)
-
\( \begin{eqnarray} \left\{ \begin{array}{l} x - 3 > -5 \\ 2x < x + 3 \end{array} \right. \end{eqnarray} \)
答え
-
数直線を用いて表すと良いですね。
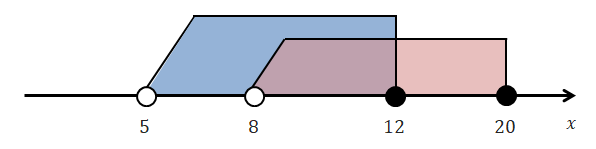
この図から共通部分を探すと答えは\(8 < x \leqq 12\)だと分かります。
-
まずはそれぞれの不等式を解いて\(x\)の範囲をはっきりさせましょう。 上の不等式は両辺に\(+3\),下の不等式は両辺に\(-x\)すると
\( \begin{eqnarray} \left\{ \begin{array}{l} x > -2 \\ x < 3 \end{array} \right. \end{eqnarray} \)となります。これを数直線を用いて表すと下図のようになります。
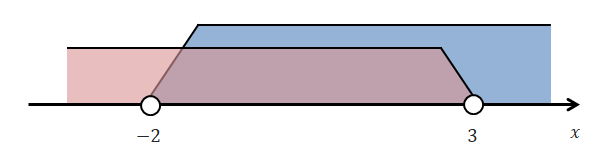
この図から共通部分を探すと答えは\(-2 < x < 3\)だと分かります。
