前回,必要十分条件を調べるとき,命題の仮定と結論を入れ替えた命題を考えました。 他にも,仮定や結論を否定することでも新しい命題が生まれます。 そうして作った命題を逆,裏や対偶といいますが,元の命題を考える上でも重要なものです。
目次
逆・裏・対偶
命題\(p \implies q\)に対して,仮定と結論を入れ替えた\(q \implies p\)を考えたい場面は多いです。 それは,\(p\)と\(q\)の関係をより詳しく知ることができるからです。
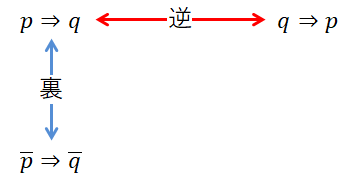
このように,命題の仮定と結論を入れ替えたものを逆といいます。

また,命題\(p \implies q\)に対して,仮定と結論をそれぞれ否定した\(\overline{p} \implies \overline{q}\)を考えることもあります。 「仮定が成り立たないとき,結論も成り立たないのか?」という新しい命題ですね。 逆と同じく,\(p\)と\(q\)の関係をより詳しく知れそうです。
このように,命題の仮定と結論をそれぞれ否定したものを裏といいます。
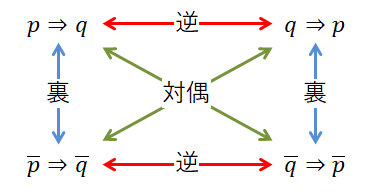
さらに,命題の仮定と結論をそれぞれ否定し,かつ入れ替えたものを対偶といいます。 命題\(p \implies q\)に対して,\(\overline{q} \implies \overline{p}\)のことですね。
逆・裏・対偶の真偽
逆・裏・対偶というものを定義してみました。 この新しい命題は,元の命題とどれほど関係があるのでしょうか? 例えば,逆について調べれば,元の命題についても新しい発見があるでしょうか?
結論からいえば,逆・裏と元の命題の真偽は無関係です。 逆・裏の真偽が分かっても,元の命題の真偽は一切分かりません。 しかし,対偶については,元の命題と真偽が一致します。
元の命題と対偶の真偽が一致することは,真理集合から確かめられます。 確認問題としておきますので,確かめてみましょう。
具体例を考えてみましょう。 「犬は哺乳類である」という命題を考えます。 仮定は「犬である」,結論は「哺乳類である」ですね。 この命題はもちろん真です。
逆は「哺乳類は犬である」ですが,これは偽ですね。 私たちヒトも哺乳類ですが,犬ではありません。 また,裏は「犬でないならば哺乳類ではない」ですが,これも偽ですね。 私たちヒトは犬ではありませんが,哺乳類です。 この通り,逆・裏と元の命題の真偽は無関係です。
対偶は「哺乳類でないならば犬ではない」ですが,これは真ですね。 犬は哺乳類なので,哺乳類でないという情報があれば,犬でないことが分かります。 この通り,対偶と元の命題の真偽は一致します。
逆・裏と元の命題の真偽は「無関係」です。 元の命題が真のとき,逆・裏が偽になるという訳ではありません。 逆・裏は真かも知れないし,偽かも知れないのです。 元の命題と反対の結果になるわけではないので注意してください。
また,前項の図を見ると分かると思いますが,逆の対偶は裏ですし,裏の対偶は逆です。 つまり,逆と裏の真偽は一致するんですね。
確認問題
命題\(p \implies q\)とその対偶\(\overline{q} \implies \overline{p}\)の真偽が一致することを,真理集合を使って確かめます。 \(p, q\)の真理集合をそれぞれ\(P, Q\)とします。
-
「\(p \implies q\)が真」と「\(P \subset Q\)」が同値であることを証明してください。
-
一般の集合\(A, B\)に対して,「\(A \subset B\)」と「\(\overline{B} \subset \overline{A}\)」が同値であることを証明してください。
-
命題\(p \implies q\)とその対偶\(\overline{q} \implies \overline{p}\)の真偽が一致することを証明してください。
答え
証明については次回本格的に扱います。 ここでは多少ゆるい書き方で証明しておきます。 \(A \iff B\)を証明するには\(A \implies B\)と\(B \implies A\)の2つを証明する必要があることに注意してください。
-
[1] 「\(p \implies q\)が真」ならば「\(P \subset Q\)」を証明します。
仮定より,\(p\)を満たすものは\(q\)を満たすので,\(x \in P\)ならば\(x \in Q\)です。 したがって,\(P \subset Q\)です。[2] 「\(P \subset Q\)」ならば「\(p \implies q\)が真」を証明します。
仮定より,\(x \in P\)ならば\(x \in Q\)です。 したがって,\(p\)を満たすものは\(q\)も満たすので,\(p \implies q\)は真です。以上から,「\(p \implies q\)が真」と「\(P \subset Q\)」は同値です。
-
\(A = \varnothing\)の場合は,\(\overline{A}\)は全体集合です。 このとき,\(B\)がどんな集合であっても,「\(A \subset B\)」と「\(\overline{B} \subset \overline{A}\)」は常に成り立ちますから,これらは同値です。 以下,\(A \neq \varnothing\)の場合を考えます。
[1] 「\(A \subset B\)」ならば「\(\overline{B} \subset \overline{A}\)」を証明します。
任意に\(\overline{B}\)の要素\(x \in \overline{B}\)を取ります。 もし\(x \in A\)とすると,仮定より\(x \in B\)となり,\(x \in \overline{B}\)に矛盾します。 よって,\(x \in \overline{A}\)でなければなりません。 したがって,\(\overline{B} \subset \overline{A}\)です。[2] 「\(\overline{B} \subset \overline{A}\)」ならば「\(A \subset B\)」を証明します。
任意に\(A\)の要素\(x \in A\)を取ります。 もし\(x \in \overline{B}\)とすると,仮定より\(x \in \overline{A}\)となり,\(x \in A\)に矛盾します。 よって,\(x \in B\)でなければなりません。 したがって,\(A \subset B\)です。以上から,「\(A \subset B\)」と「\(\overline{B} \subset \overline{A}\)」は同値です。 ちなみに,ここでは次回学ぶ「背理法」の考え方を使っています。
-
命題の真偽が一致することを証明するには,「それらの命題がいつ真になるか」が一致することを示せばいいですね。
(1)より,\(p \implies q\)が真であることは,\(P \subset Q\)と同値です。 同様に,\(\overline{q} \implies \overline{p}\)が真であることは,\(\overline{Q} \subset \overline{P}\)と同値です。 ここで(2)より,\(P \subset Q\)と\(\overline{Q} \subset \overline{P}\)は同値です。
したがって,\(p \implies q\)が真であることと,\(\overline{q} \implies \overline{p}\)が真であることは同値であり,これらの真偽が一致することが分かりました。
次の命題に対して,逆・裏・対偶がどのような命題か答えてください。 また,元の命題とその逆・裏・対偶それぞれについて,真偽を答えてください。
\(x, y\)は非負の実数とします。
-
\(xy = 0\)ならば,\(x = 0\)または\(y = 0\)
-
\(xy \geqq 6\)ならば,\(x \geqq 2\)または\(y \geqq 3\)
答え
元の命題の真偽は,その対偶の真偽と一致します。 ここでは,元の命題の真偽については,対偶を通して考えてみましょう。
-
逆は「\(x = 0\)または\(y = 0\)ならば,\(xy = 0\)」で,真です。
裏は「\(xy \neq 0\)ならば,\(x \neq 0\)かつ\(y \neq 0\)」で,真です。 裏の真偽は,逆の真偽と一致するんでしたね。
対偶は「\(x \neq 0\)かつ\(y \neq 0\)ならば,\(xy \neq 0\)」で,真です。
元の命題の真偽は,対偶の真偽と一致しますから,元の命題は真です。
-
逆は「\(x \geqq 2\)または\(y \geqq 3\)ならば,\(xy \geqq 6\)」で,偽です。 例えば,仮定を満たす\(x, y\)として\(x = 2, y = 1\)がありますが,このとき\(xy = 2\)であり,結論を満たしません。
裏は「\(xy < 6\)ならば,\(x < 2\)かつ\(y < 3\)」で,偽です。 反例としては,逆の場合と同じ\(x, y\)が挙げられます。 裏の真偽は,逆の真偽と一致するんでしたね。
対偶は「\(x < 2\)かつ\(y < 3\)ならば,\(xy < 6\)」で,真です。 \(x, y\)が非負という条件があるためです。
元の命題の真偽は,対偶の真偽と一致しますから,元の命題は真です。
