証明問題を解くには,単純な計算問題よりも論理的思考を要求されます。 それは,数学を通して習得すべき最も重要なスキルです。 ここでは,そのための考え方の基本を紹介します。
目次
証明の基本方針
証明問題というと,何にどう手を付けたら良いかすら分からないかも知れません。 ここでは,証明のための基本方針を紹介していきます。
証明のステップはざっくり3段階です。 まずは,与えられた情報を整理します。 次に,それらの情報を繋ぐ道筋を考えます。 最後に,それを文章で表します。
第一ステップは情報整理です。 仮定(与えられた条件)と結論(証明したいこと)をはっきりさせましょう。
与えられていない条件を勝手に使ってしまったり,議論の着地点を見失ったりしないように気を付けましょう。
仮定と結論という言葉に引っ張られて,問題を無理矢理\(p \implies q\)の形に直す必要はありません。 大事なのは,「使ってもいい情報は何か」と「その情報を元に何を言いたいか」を確認することです。
「整数と無理数の和は無理数である」という命題であれば,使ってもいい情報は,和をとる数が「整数」と「無理数」であることです。 もちろん勝手に有理数として扱ったりしてはいけません。 そしてこの情報を元に「その和が無理数」になることを証明します。
第二ステップは具体的な考察です。 仮定の情報と数学的知識を元に,結論にたどり着くためにどうするか考えます。 このステップが最も重要で,また難しいところです。
仮定の情報を闇雲に使っても結論にはたどり着けません。 まずやるべきことは,結論を得るために何が必要かを考えることです。 つまり,大きな問題を小さな問題に分解することです。
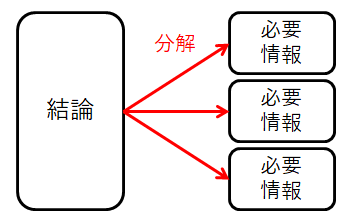
ここでいう分解とは,問題を考えやすい必要十分条件に置き換えることです。
例えば,「無理数であること」を直接証明するのは難しいです。 しかし,無理数とは実数のうち有理数でないものですから,「実数であること」「有理数でないこと」の2つを証明すれば,無理数であることが証明できます。 より扱いやすい2つの問題に置き換えたわけです。
場合によっては,小さな問題への分解は何度か行います。 そうして解決可能な問題にまで分解するのです。
問題を分解したときのイメージが下図です。 実際の証明の際にこの図を書く必要はありませんが,この図がそのまま証明の設計図にもなります。 黄色部分を証明して矢印を逆にたどれば,結論にたどり着くわけです。
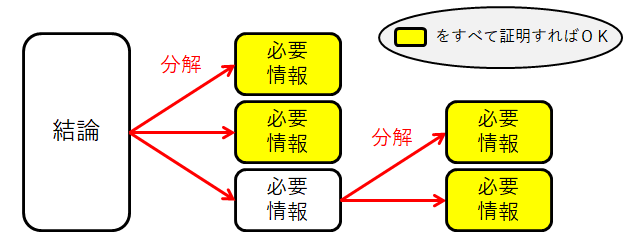
証明の設計図ができあがったので,あとは黄色部分を証明するだけです。 証明に使ってもいい情報は「問題の仮定」と「数学的知識」だけです。
仮定は第一ステップで確認したもので,証明に使う「材料」です。 数学的知識は,学校で習った定理や公式のことで,材料を加工する「道具」です。 仮定は問題文を見れば必ず分かりますが,知識は勉強の成果が問われるところです。
証明問題で前提として良い知識は,学校で習う範囲のものです。 学校で習わない便利な定理もありますが,それは使えません。 もちろん,それを自分で証明してからであれば使ってもOKです。
第三ステップは証明の記述です。 記述の内容は,第二ステップでできた設計図の内容です。 記述の際には接続詞をきちんと使うことを心掛けましょう。
証明の記述は,論理の流れが見えることが重要です。 「~である。~である。~である。」という記述ではそれが分かりません。 接続詞を適宜使いましょう。
「よって,したがって,また,つまり,すなわち,なぜなら,ゆえに」などの接続詞をよく使います。 内容によっては,「まず,次に,最後に」なども使います。 証明の最後は「以上より,~である。」のように締めくくることが多いですね。
背理法
ここからは一般論ではなく,証明のテクニックを見ていきましょう。 中でも代表的なのが背理法です。
背理法とは,結論が成り立たないと仮定し,矛盾を導く証明方法です。 「これが成り立たないとしてみて?おかしなことになっちゃうよ?」という流れですね。
背理法が有効とされる代表的な問題が,「\(\sqrt{2}\)が無理数であることを証明せよ」ですね。 \(\sqrt{2}\)が有理数であると仮定して矛盾を導くのですが,確認問題にしてあるので解いてみてください。
背理法を使わなければ解けない問題はありません。 しかし,以下のような場合には,背理法を使うことで問題を分かりやすくすることができます。
ひとつは,命題が「~でない」という形になっている場合です。 「~でない」より「~である」の方が,主張がはっきりしていて考えやすいと思いませんか? そんなときは「~である」と仮定して矛盾を導く背理法が有効です。
もうひとつは,命題が「少なくとも~である」という形になっている場合です。 これも「全く~でない」の方が,主張がはっきりしていて考えやすいため,背理法が有効です。
このように,背理法は問題の見方を少し変えることで,考えやすい形にする方法です。
対偶法
前回,命題とその対偶の真偽が一致することを学びました。 ということは,ある命題を証明するために,代わりにその対偶を証明しても良いわけです。 対偶を証明することで命題を証明する方法を対偶法といいます。
対偶法を使う場面は背理法ほど多くないですが,命題が証明しづらいなーと感じたら,対偶法を試してみると良いかもしれません。
命題の証明は,仮定を元にして結論にたどり着くものです。 なので,仮定は簡単な内容であった方が,扱いやすくて便利です。
一方,命題の対偶をとると,仮定と結論が(否定の形で)入れ替わります。 命題の真偽はそのままに,入れ替えられるのです。
以上を考慮すると,仮定が結論よりも複雑な場合,対偶法が有効に使えます。 例えば,「\(n^2\)が\(3\)の倍数ならば,\(n\)は\(3\)の倍数である」の証明には対偶法が有効です。
反例
ここまで命題が成り立つことの証明の仕方を学びました。 次は命題が成り立たないことの証明について考えましょう。
命題が成り立たないことを証明するには,命題の否定が成り立つことを証明するか,反例を挙げれば良いです。 命題の否定の証明については,通常の命題の証明と同様です。
反例とは,命題が成り立たない具体例です。 つまり,命題の仮定を満たすのに,結論は満たさない例です。 反例をひとつ挙げるだけで,命題が成り立たないことが証明できます。
「\(x + y \leqq 2\)ならば,\(x \leqq 1\)かつ\(y \leqq1\)」という命題は偽です。 反例としては,\(x = 1.5, y = 0\)や\(x = 0.5, y = 1.2\)などが挙げられます。 どちらも仮定は満たしますが,結論は満たしません。
しかし,例えば\(x = 2, y = 2\)は反例にはなりません。 これは確かに結論は満たしませんが,仮定も満たしていないからです。 仮定を満たさない例は,もはや命題とは全く関係ありません。
例えば「哺乳類は卵を生まない」という命題は偽ですが,「インコ」は反例になりません。 確かにインコは卵を生みますが,哺乳類という仮定を満たさないので,この命題とは全然関係ないのです。 正しい反例は,哺乳類でありながら卵を生む「カモノハシ」や「ハリモグラ」です。
確認問題
任意の整数\(n\)について,\(n^2 + n\)が偶数であることを証明してください。
【ヒント】偶数は整数\(a\)を用いて\(2a\)と,奇数は\(2a + 1\)と表せます。
答え
\(n\)が整数という情報を使って,\(n^2 + n\)が偶数であるという結論にたどり着くのが目的です。 どうやって結論にたどり着けば良いでしょうか? ふたつの考え方が思いつきます。
ひとつは,\(n^2 + n\)が和の形になっていることに注目します。 整数の和が偶数になるのは,「偶数\(+\)偶数」か「奇数\(+\)奇数」の場合のみです。 どんな\(n\)に対してもこの形に落ち着くことを証明できれば良さそうです。 したがって,次のような解答例が考えられます。
\(n\)は整数であるから,\(n^2, n\)はともに整数である。 したがって,\(n^2 + n\)が偶数になるのは,\(n^2, n\)がともに偶数であるか,ともに奇数である場合のみであり,任意の整数\(n\)に対しそうなることを証明すればよい。
[1] \(n\)が偶数の場合
\(n\)は整数\(a\)を用いて\(n = 2a\)と表せる。
このとき,\(n^2 = 4a^2\)であり,\(a^2\)は整数であるから,\(n^2\)も偶数である。
したがって,\(n^2 + n\)は偶数となる。
[2] \(n\)が奇数の場合
\(n\)は整数\(a\)を用いて\(n = 2a + 1\)と表せる。
このとき,\(n^2 = 4a^2 + 4a + 1 = 2(2a^2 + 2a) + 1\)であり,\(2a^2 + 2a\)は整数であるから,\(n^2\)も奇数である。
したがって,\(n^2 + n\)は偶数となる。
以上から,任意の整数\(n\)に対し,\(n^2 + n\)は偶数である。
もうひとつは,\(n^2 + n = n(n + 1)\)と因数分解してみると,これが積の形になっていることに注目します。 整数の積が偶数になるのは,積をとる数の少なくとも片方が偶数である場合のみです。 どんな\(n\)に対してもこの形に落ち着くことを証明できれば良さそうです。 したがって,次のような解答例が考えられます。
\(n\)は整数であるから,\(n, n + 1\)はともに整数である。
したがって,\(n^2 + n = n(n + 1)\)が偶数になるのは,\(n\)または\(n + 1\)が偶数の場合であり,任意の整数\(n\)に対しそうなることを証明すればよい。
[1] \(n\)が偶数の場合
\(n^2 + n = n(n + 1)\)は偶数である。
[2] \(n\)が奇数の場合
\(n\)は整数\(a\)を用いて\(n = 2a + 1\)と表せる。
このとき,\(n + 1 = 2a + 2 = 2(a + 1)\)であり,\(a + 1\)は整数であるから,\(n + 1\)は偶数である。
したがって,\(n^2 + n = n(n + 1)\)は偶数である。
以上から,任意の整数\(n\)に対し,\(n^2 + n\)は偶数である。
三角形の内角の少なくとも1つは\(60^{\circ}\)以上であることを証明してください。
答え
「少なくとも」というのは考えづらいです。 ここは背理法を使って,「少なくとも」を「全く~でない」に変えて考えましょう。 解答例は次のようになります。
三角形の3つの内角を\(A, B, C\)とする。 三角形の内角が全て\(60^{\circ}\)未満であると仮定すると,\(0^{\circ} < A, B, C < 60^{\circ}\)である。 このとき,内角の和は\(0^{\circ} < A + B + C < 180^{\circ}\)となり,三角形の内角の和が\(180^{\circ}\)であることに矛盾する。 したがって,三角形の内角の少なくとも1つは\(60^{\circ}\)以上である。
次の命題を証明してください。
ただし,有理数は整数\(a, b\)を使って,既約分数\(\displaystyle\frac{b}{a}\)で表せることを使ってOKです。 既約分数とは,それ以上約分できない分数のことです。 ちなみに,このとき\(a, b\)は互いに素であるといいます。(数学Aで学習します。)
-
整数\(x\)について,\(x^2\)が偶数ならば,\(x\)は偶数である。
-
\(\sqrt{2}\)は無理数である。
答え
-
仮定には\(x^2\),結論には\(x\)が登場しています。 このように結論の内容の方が簡単な場合,対偶をとった方が考えやすいです。 解答例は次のようになります。
命題とその対偶の真偽は一致するため,対偶を証明すればよい。 命題の対偶は,「\(x\)が奇数ならば,\(x^2\)は奇数である」となる。
\(x\)が奇数のとき,整数\(a\)を用いて\(x = 2a + 1\)と表せる。 このとき,\(x^2 = 4a^2 + 4a + 1 = 2(2a^2 + 2a) + 1\)であり,\(2a^2 + 2a\)は整数であるから,\(x^2\)も奇数である。 したがって,対偶は真であるから,題意の命題も真である。
-
無理数はちょっと扱いづらい数です。 ここは背理法を使って,有理数で議論できるようにしましょう。 解答例は次のようになります。
\(\sqrt{2}\)が無理数でないと仮定すると,\(\sqrt{2}\)は有理数であり,整数\(a, b\)を用いて\(\sqrt{2} = \displaystyle\frac{b}{a}\)と表せる。 ただし,これは既約分数である。
式を変形すると,\(\sqrt{2}a = b\)となり,両辺を2乗すると\(2a^2 = b^2\)となる。 ここで,\(a^2\)は整数であるから,\(b^2\)は偶数であり,(1)より\(b\)も偶数である。 よって,\(b\)は整数\(n\)を用いて\(b = 2n\)と表せる。
これを\(2a^2 = b^2\)に代入すると,\(a^2 = 2n^2\)となる。 ここで,\(n^2\)は整数であるから,\(a^2\)は偶数であり,(1)より\(a\)も偶数である。
したがって,\(a\)と\(b\)はともに偶数であり,共通因数\(2\)をもつから,\(\displaystyle\frac{b}{a}\)が既約分数であることに矛盾する。 以上から,\(\sqrt{2}\)は無理数である。
素数が無限個存在することを証明してください。
【ヒント】\(2\)以上の自然数\(a_1, a_2, \cdots, a_n\)の積\(a_1a_2 \cdots a_n\)に\(1\)を加えた\(a_1a_2 \cdots a_n + 1\)は,\(a_1, a_2, \cdots, a_n\)のどれで割っても\(1\)余ります。
答え
「無限」というものを考えるのは難しそうです。 背理法を使えば,「有限」のものについて考えられるようになります。 解答例は次のようになります。
素数が有限個しか存在しないと仮定する。 素数の個数を\(n\)とし,\(a_1, a_2, \cdots, a_n\)をすべての素数とする。
ここで,\(A = a_1a_2 \cdots a_n + 1\)とすると,\(A\)はどの素数よりも大きな数であるから,\(A\)自身は素数ではなく,\(a_1, a_2, \cdots, a_n\)のいずれかで割り切れる。 しかし,\(A\)は\(a_1, a_2, \cdots, a_n\)のどれで割っても\(1\)余り,矛盾が生じる。 この矛盾は,素数が有限個とする仮定から導かれたため,素数は無限個存在する。
「実数\(x, y\)について,\(xy^2 \leqq 18\)ならば,\(x \leqq 2\)または\(y \leqq 3\)である」という命題があります。 これを次に指定された方法で証明してください。
-
背理法
-
対偶法
-
背理法も対偶法も使わない
答え
背理法・対偶法を使う場合については,特に難しいところはないと思います。 (3)については,仮定の式を変形して結論にもっていきます。 結論が「\(A\)または\(B\)」の形をしている場合は,「\(A\)が成り立たないならば,必ず\(B\)が成り立つ」ということを証明できればOKです。
-
\(xy^2 \leqq 18\)のときに,\(x > 2\)かつ\(y > 3\)であると仮定する。 このとき,\(xy^2 > 2 \cdot 3^2 = 18\)より,\(xy^2 \leqq 18\)に矛盾する。 したがって,このとき\(x \leqq 2\)または\(y \leqq 3\)である。
-
命題の対偶をとると,「\(x > 2\)かつ\(y > 3\)ならば,\(xy^2 > 18\)である」となる。 対偶の仮定のもとでは,\(xy^2 > 2 \cdot 3^2 = 18\)であるから,この対偶は真である。 したがって,元の命題も真である。
-
\(xy^2 \leqq 18\)のとき,\(y\)の値は\(y \leqq 3\)か\(y > 3\)のいずれかである。 \(y \leqq 3\)の場合,結論が成り立つ。 \(y > 3\)の場合,\(y^2 > 0\)に注意すると,\(xy^2 \leqq 18\)から\(x \leqq \displaystyle\frac{18}{y^2} < \displaystyle\frac{18}{3^2} = 2\)となり,結論を満たす。 以上から,すべての場合に対し結論が成り立つため,命題は真である。
次の命題について,真ならそれを証明し,偽なら反例を挙げてください。
-
整数と無理数の和は無理数である。
-
無理数と無理数の和は無理数である。
答え
-
整数を足しても小数部分は変わらないので,無理数は無理数のままだろうと見当がつきます。 解答例は次のようになります。
命題は真である。このことを証明する。 ある整数\(a\)とある無理数\(x\)に対し,その和が有理数\(r\)になると仮定する。 このとき,\(a + x = r\)から,\(x = r - a\)である。 しかし,この等式の右辺は有理数であり,左辺が無理数であることに矛盾する。 したがって,和が有理数となるような整数と無理数の組み合わせは存在せず,整数と無理数の和は無理数となることが示された。
-
無理数と無理数の和は無理数になるとは限りません。 最も簡単な例は,和が\(0\)になる場合です。 解答例は次のようになります。
命題は偽である。反例としては,\(\sqrt{2}\)と\(-\sqrt{2}\)という2つの無理数の和が\(0\)という有理数になることが挙げられる。
