２次関数第 1 回

関数とグラフ

◀

証明

２次関数のグラフ

▶

はじめに

関数は，いくつかの数の関係を表しています。 関係といっても色々考えられますが，関数の場合は「ＡがこうならＢはどうなる？」みたいな関係を表します。 そしてその関係を可視化したものがグラフです。

目次

関数と定義域・値域

▼

関数にも色々種類があるのですが，ここでは１変数のものを説明します。

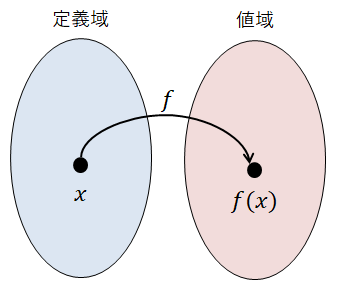
関数とは，ある値をもとに新しい値を作り出すものです。 もとにする値を変数\(x\)，関数の名前を\(f\)で表すとき，この関数を\(f(x)\)か，単に\(f\)と表します。

\(x\)がある値\(a\)をとるとき関数が作り出す値を，\(x = a\)における関数\(f(x)\)の値といい，\(f(a)\)と表します。 例えば\(f(x) = x^3 - 1\)のとき，\(f(2) = 2^3 - 1 = 7\)です。

補足 多変数関数

上の説明で扱ったのは１変数関数のみですが，２変数以上の関数も存在します。 ただし，多変数だとその分難しくなるので，高校数学ではあまり出てきません。

２つの変数\(x, y\)の値を決めると，それに応じて新しい値を作り出すものを２変数関数\(f(x, y)\)といいます。 同様にもっと複雑な多変数関数も考えられます。

関数の値を変数\(y\)にしまうことにして，\(y = f(x)\)という等式を考えると，関数の別の側面が見えてきます。 このとき，変数\(x, y\)の間には，\(x\)の値が決まるとそれに応じて\(y\)の値が決まるという関係があります。 関数は２つの変数のこのような関係を表すものでもあるのです。

このとき，\(y\)は\(x\)の関数であるといい，\(x\)を独立変数，\(y\)を従属変数といいます。 独立変数である\(x\)は自分で決めることができますが，従属変数である\(y\)は自分では決められません。 \(y\)は\(x\)を決めたときに勝手に決まるのです。

補足 記号について

上の説明では\(x, y, f\)という文字を使いましたが，これは決められたものではありません。 別に\(b = c(a)\)でも\(\eta = \Omega(\xi)\)でも何でもＯＫです。 ただ関数は英語で function というので，頭文字の\(f\)や次のアルファベットの\(g, h\)を使うことが多いです。

関数や方程式などの用語がごっちゃになる人は，こちらも参考にしてみてください。

関数の例として，\(x\)メートルを\(y\)フィートに直す\(y = 3.281x\)がありますが，この\(x\)は正の値である必要がありますね。 もちろん\(y\)も必ず正です。 このように，関数の変数はどんな値でも良いとは限りません。

上で見たように，関数\(y = f(x)\)の\(x\)には取りうる値の範囲があり，これを定義域といいます。 \(x\)が定義域の値しか取れないので，\(x\)によって決まる\(y\)も特定の値しか取れません。 \(y\)が取りうる値の範囲を値域といいます。

定義域，値域は変数の取りうる値の範囲ですから，\(x\)や\(y\)の不等式で表します。 例えば，\(2 < x < 5\)を定義域とする関数\(y = x^2\)の値域は\(4 < y < 25\)です。 また，関数と定義域をセットで書くときは，\(y = x^2 \quad (2 < x < 5)\)のように書くことが多いです。

補足 写像

ここまでの説明から，関数とは，定義域の値を値域の値に対応させるものであることが分かります。 このような対応は，数と数の関係でなくても，色々な集合で考えられます。

集合\(A, B\)に対して，\(A\)の各要素に\(B\)の要素をただ一つ対応させる規則\(f\)を，始域\(A\)から終域\(B\)への写像といい，\(f: A \rightarrow B\)などと書きます。 関数も写像の一つで，始域を定義域，終域を値域といいましたね。

座標平面とグラフ

▲
▼

関数\(y = f(x)\)がどんな関数か考えるとき，どうすると良いでしょう？ そのシンプルな答えは，定義域の各値に対して，関数がとる値を列挙することです。 しかし，すべてを列挙することは現実的ではなさそうです。

そこで，関数のグラフという概念を導入します。 定義域の各値\(x = a\)と，関数がとる値\(f(a)\)を組にした\((a, f(a))\)を考えます。 これをすべて集めた集合を，関数\(f\)のグラフといいます。

グラフは関数の特徴を端的にとらえるものです。 しかし，せっかくのグラフも，扱い方を知らなければ役に立ちません。 ここからはグラフの図示の仕方を学ぶことにします。

グラフの要素は２つの実数の組ですね。 １つの実数を図示するときは，数直線というツールを使いました。 では２つの実数の組を図示するときはどうするか？数直線を２つ使えば良いのです。

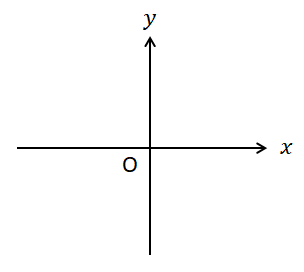
下図のように，２本の数直線を垂直に交差させたものが座標平面です。 また，この２本の数直線を座標軸といいます。 座標軸の交差点は数直線の原点に合わせ，Ｏで表します。 座標軸の\(x, y\)は２つの実数を表す変数で，それぞれの座標軸を\(x\)軸，\(y\)軸といいます。 また，このとき座標平面を\(xy\)平面といいます。

補足 \(x\)と\(y\)

上の説明では\(x, y\)という変数を使いましたが，必ず\(x, y\)でないといけないわけではありません。 別に\(a, b\)や\(s, t\)といった変数を使っても問題ありません。

変数に\(a, b\)を使うときは\(ab\)平面や\(a\)軸，\(b\)軸などといい，\(s, t\)を使うときは\(st\)平面や\(s\)軸，\(t\)軸などといいます。 いま使っている変数が何かに気を付けて，使う言葉を間違えないようにしましょう。

座標平面のそれぞれの数直線からひとつずつ値をとることで，２つの実数の組を表現できます。 \(x\)軸から\(a\)，\(y\)軸から\(b\)をとったときの組を\((a, b)\)と書きます。 例えば\((2, 3)\)は下図の点で表せます。

逆に，座標平面上の点は\(x\)軸，\(y\)軸からとった２つの実数の組で表せ，座標といいます。 ２つの実数のうち\(x\)軸，\(y\)軸からとった値をそれぞれ\(x\)座標，\(y\)座標といいます。 下図の点の座標は\((2, 3)\)で，\(x\)座標は\(2\)，\(y\)座標は\(3\)ですね。

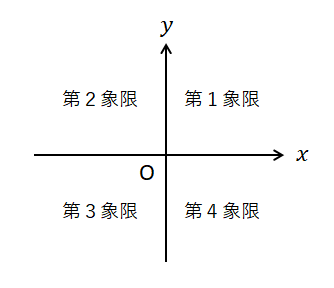
また，座標平面は座標軸によって４つの部分に区切られていますが，それぞれ第１～第４象限といいます。 順番は右上から反時計回りです。 座標軸上の点はどの象限にも属さないので注意です。

ここまで，２つの実数の組を図示できる座標平面を考えました。 これで関数のグラフを図示する準備が整いました。 グラフの要素をすべて座標平面に図示することで，関数の特徴を視覚的に捉えられます。

例として，\(y = 3x + 1\)という関数のグラフを考えましょう。 そのためにグラフの要素をいくつか調べます。 \(x\)に適当な値を入れることで，\((0, 1), (1, 4), (2, 7)\)などの要素があることが分かります。 それらの点を\(A, B, C\)とし，座標平面にかいて線で繋ぐと，下図のようになります。

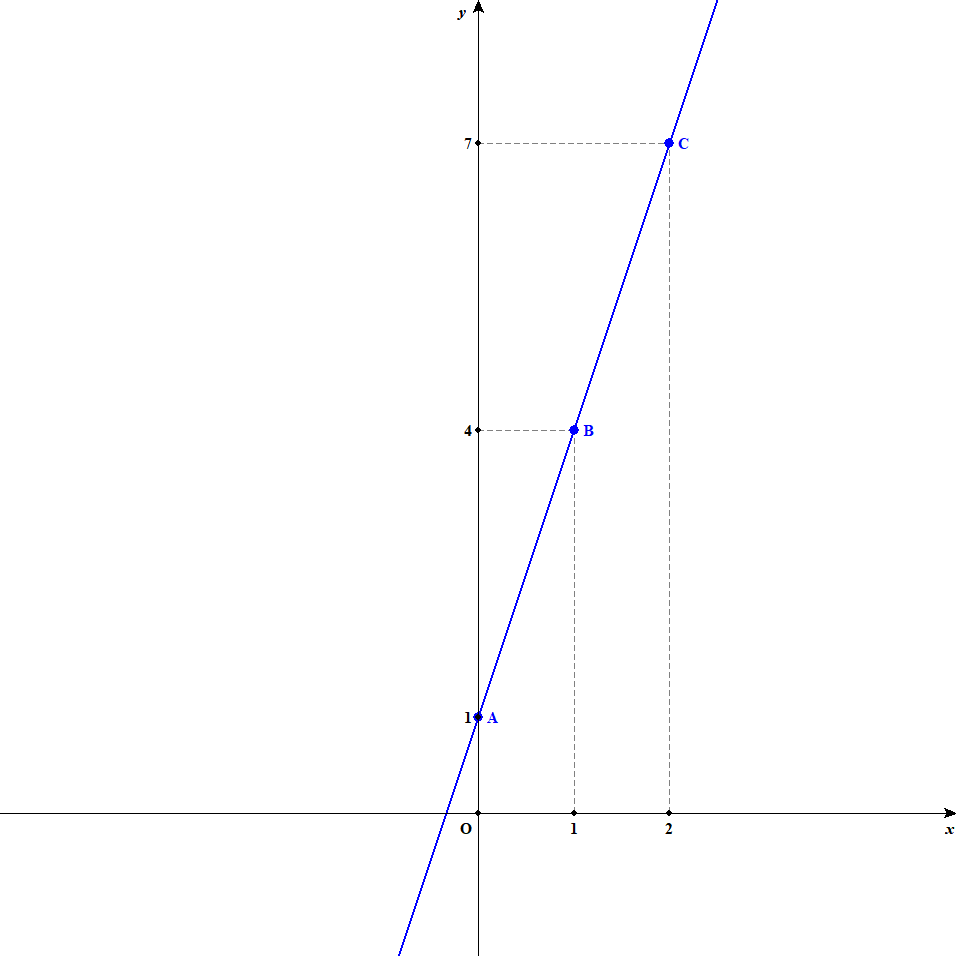
ただし，この図でちゃんと確認したのは\(A, B, C\)の３点だけで，それ以外は点同士を繋げたり延長してみただけです。 この関数のグラフはこれで正しいのですが，本当なら数個の点を調べたくらいでグラフの形は分かりません。

関数のことを調べるときにグラフは便利ですが，その完璧な形はなかなか分かりません。 関数ごとのグラフの概形などはあらかじめ知っておく必要があります。

補足 グラフの形を知るには

今のところ，関数ごとのグラフの形は，知識として持っておくしかありません。 これから１次関数，２次関数，三角関数など色々な関数を個別に学んでいきます。

しかし，数学Ⅱ・Ⅲの微分法を学ぶことで一気に世界が広がります。 全く知らない関数でも，グラフの形を自力で調べられるようになるので，楽しみにしておいてください。

補足 グラフのかき方

グラフは線だけかいても，それが正しいかどうか判断できません。 必ずグラフ上の点の座標をいくつか，最低でも２つは明記しましょう。

特に\(x\)切片，\(y\)切片，定義域の端の点，グラフを特徴付ける点は明記しておきましょう。 グラフを特徴付ける点については，これから都度説明していきます。

１次関数

▲
▼

関数をグラフで考える準備が整ったので，具体例として，簡単な１次関数について考えてみましょう。

１次関数は，名前の通り１次式の形をした関数です。 つまり，１次関数は定数\(a, b\)を用いて\(y = ax + b\)と表せます。 また，中学で学んだ通り，１次関数のグラフは直線です。 \(a\)は直線の傾き，\(b\)は\(y\)切片になります。 また，\(y = ax + b\)を直線の方程式ともいいます。

傾きは直線の傾き具合で，\(x\)が\(1\)増える間に\(y\)が増える量を表します。 \(y\)切片は直線が\(y\)軸とぶつかる点です。 では，少し具体例を見てみましょう。

まずは傾きがグラフの形にどう影響するのか見てみましょう。 下図は傾きが\(-1, -3, 3, 1\)の４本の直線をひとつの図にまとめたものです。 \(y\)切片はすべて共通で\((0, 1)\)です。

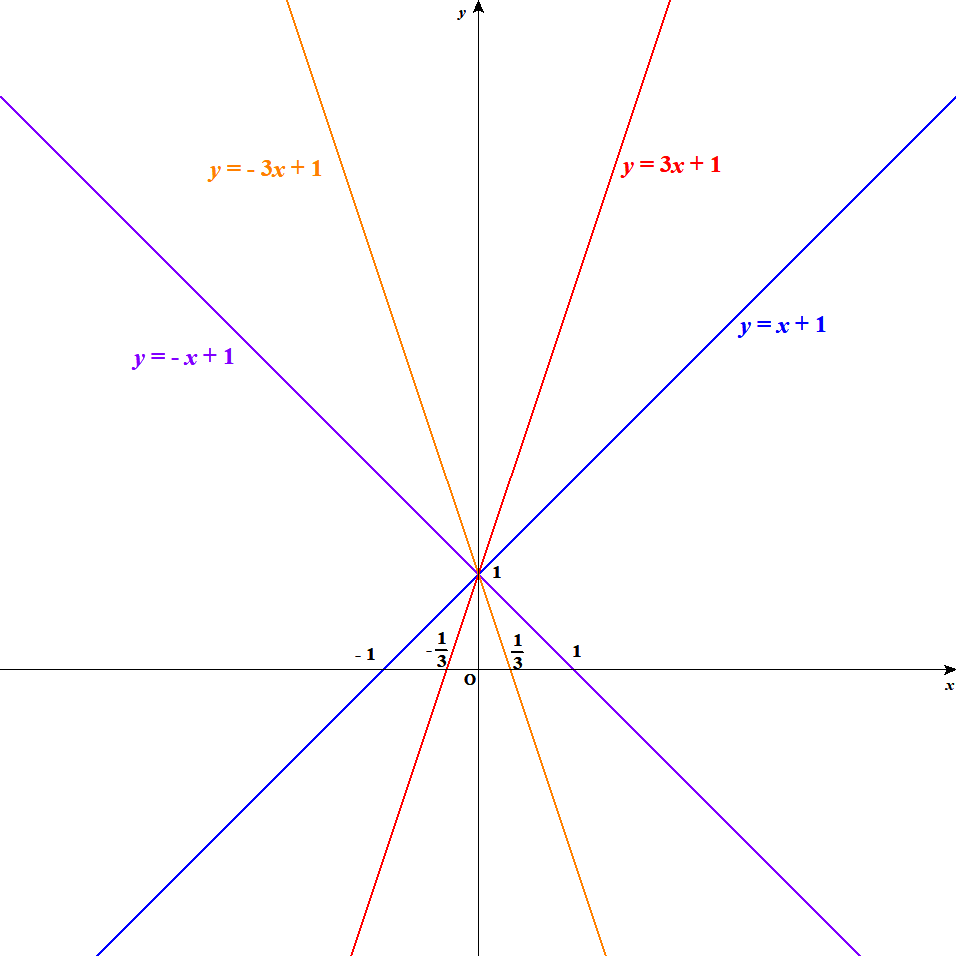
こうしていくつかの傾きを比べてみると，２つのことに気が付きます。 ひとつは，傾きが正のときはグラフが右上がり，傾きが負のときは右下がりになることです。 もうひとつは，傾きの絶対値が大きいほどグラフが急勾配になることです。

次に\(y\)切片がグラフの形にどう影響するのか見てみましょう。 下図は\(y\)切片の\(y\)座標が\(-1, 1, 3\)の３本の直線をひとつの図にまとめたものです。 傾きはすべて共通で\(1\)です。

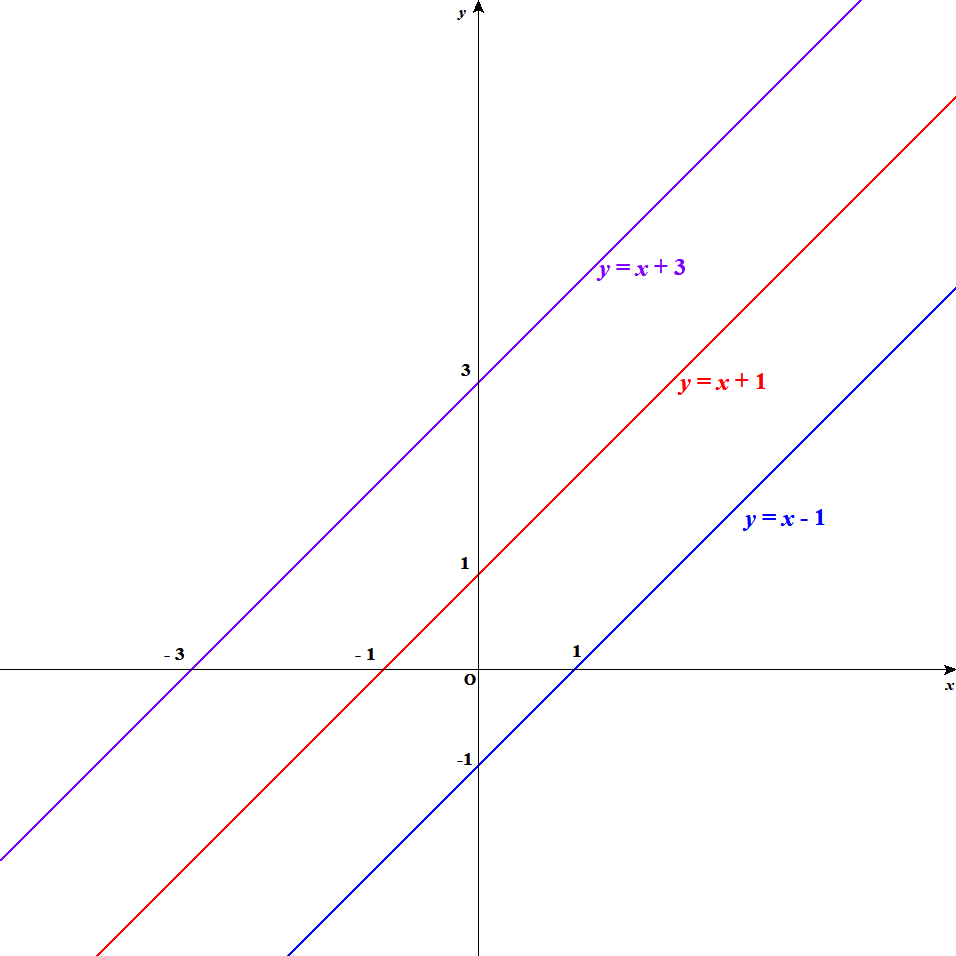
こうしていくつかの\(y\)切片を比べてみると，\(y\)切片はグラフの縦方向の位置に関わっていることが分かります。 傾きと違って，\(y\)切片の正負でグラフの性質は大きく変わりません。

１次関数のグラフをかくときは，上の例のように，必ず直線上の点の座標を２つ明記します。 基本的には\(x\)切片と\(y\)切片の座標をかいておけば問題ないですが，直線が原点を通るときは，原点の他にもうひとつ適当な点の座標をかいておきましょう。

関数の最大値と最小値

▲
▼

関数について調べるとき，そのグラフをかけば色々なことが分かります。 例えば，関数の値が最も大きくなるときや，小さくなるときがいつなのかが視覚的に分かります。

関数がとる最大の値を最大値，最小の値を最小値といいます。 これは関数を考える上でとても重要な情報です。 例えば，いつ報酬がたくさん貰えるかとか，いつ損失が最も抑えられるかなどが考えられます。

例として，\(-1 \leqq x \leqq 2\)を定義域とする関数\(y = -x^2 + 3\)について考えてみましょう。 関数のグラフは下図のようになります。

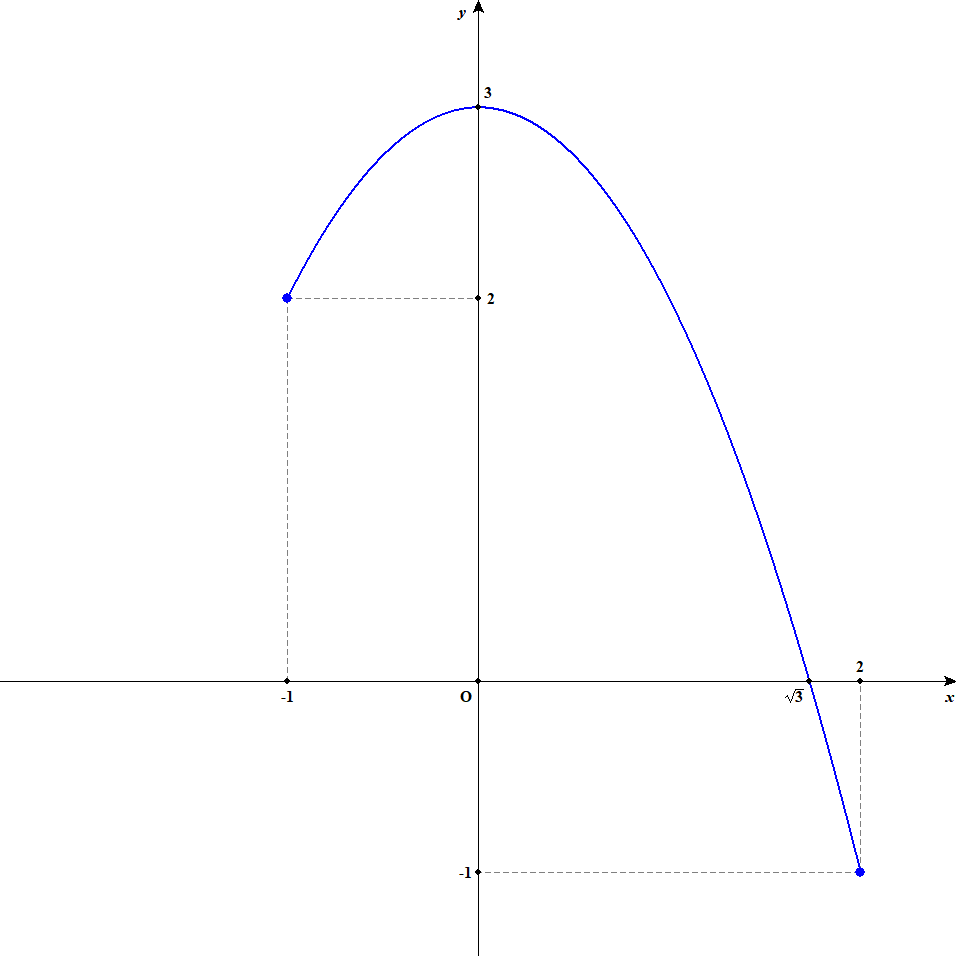
２次式の関数については次回以降学びますが，今回は目分量でグラフを見てみます。 最大値は\(y\)が最も大きいところですから，\(x = 0\)のときに最大値\(3\)をとっていますね。 最小値は\(x = 2\)のとき\(-1\)です。

最大値・最小値は値そのものだけでなく，いつその値をとるかということも重要な情報です。 問題で最大値・最小値を聞かれたら，上の例のように「\(x = \Box\)のとき最大値\(\triangle\)をとる」と答えましょう。

注意ですが，最大値・最小値は存在しないこともあります。 次のグラフはすべて最大値が存在しないものの例です。 最小値にも同じような例が考えられます。

まず下図を見てください。

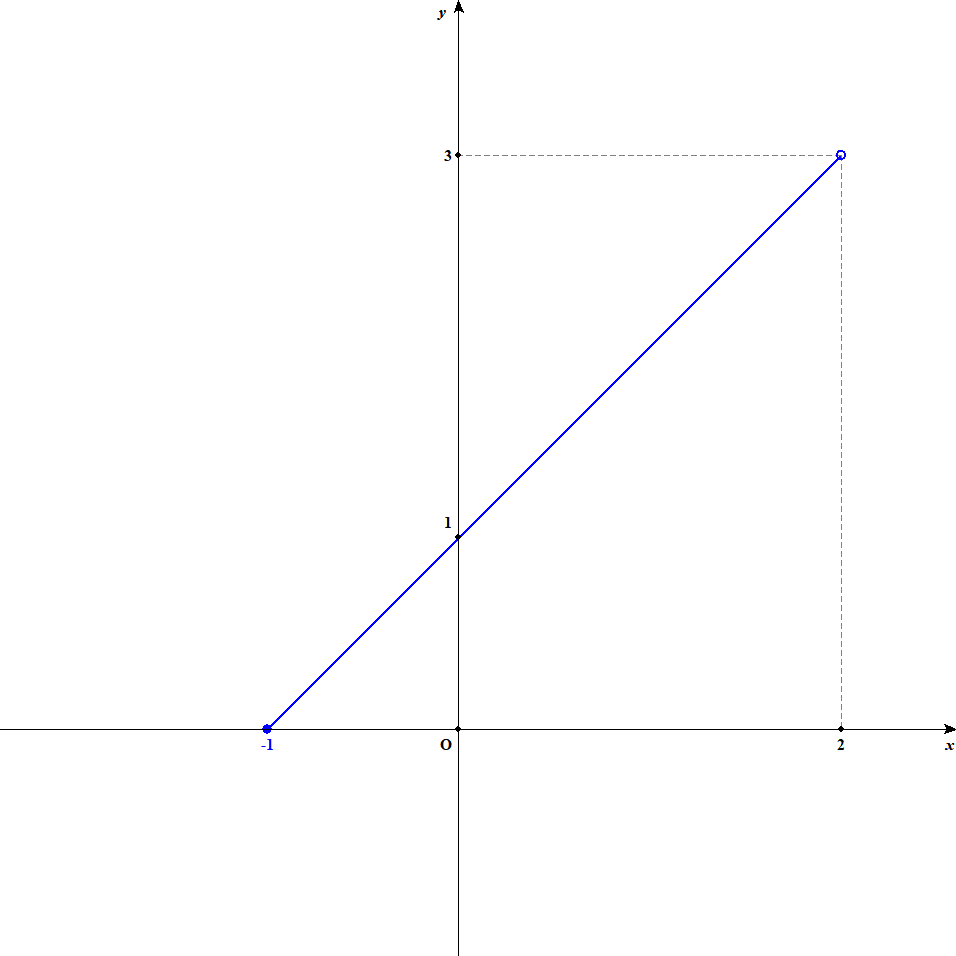
これは\(y = x + 1\)のグラフですが，定義域が\(-1 \leqq x < 2\)になっています。 一見すると\(x = 2\)のとき最大値として\(3\)をとりそうですが，\(x = 2\)は定義域に含まれていませんから，最大値ではありません。

補足 定義域の端

１次不等式で使ったのと同じように，定義域の端の値をとりうるときはグラフの端を黒丸，とらないときは白丸で表現します。

それなら\(x = 2\)の手前が最大値になりそうですが，そもそも「\(x = 2\)の手前」というものは存在しません。 \(x = 1.9\)を考えてもそれより大きい\(x = 1.95\)がありますし，\(x = 1.999\)を考えてもそれより大きい\(x = 1.9995\)があります。

いかにも最大がありそうなこのグラフですが，実は最大値が存在しないのです。 なぜなら，定義域内でいくらでも大きな値を考えられるので，「最も大きい」ものはないからです。

補足 上限

上の例では，グラフの見た目的には右端が一番大きいのに，最大値が存在しないので気持ち悪いですね。 この関数には最大値はありませんが，「上限」は存在します。 もちろん上限は\(3\)です。

上限は高校数学では登場しないので覚える必要はありません。 定義も高校レベルでは難しいので説明しませんが，ちゃんとこういう端の値を考えられる概念もあるんですよーという紹介だけさせてもらいました。 あ，もちろん「下限」という概念もありますよ。

もうひとつ最大値が存在しない例を見ましょう。 次の図を見てください。

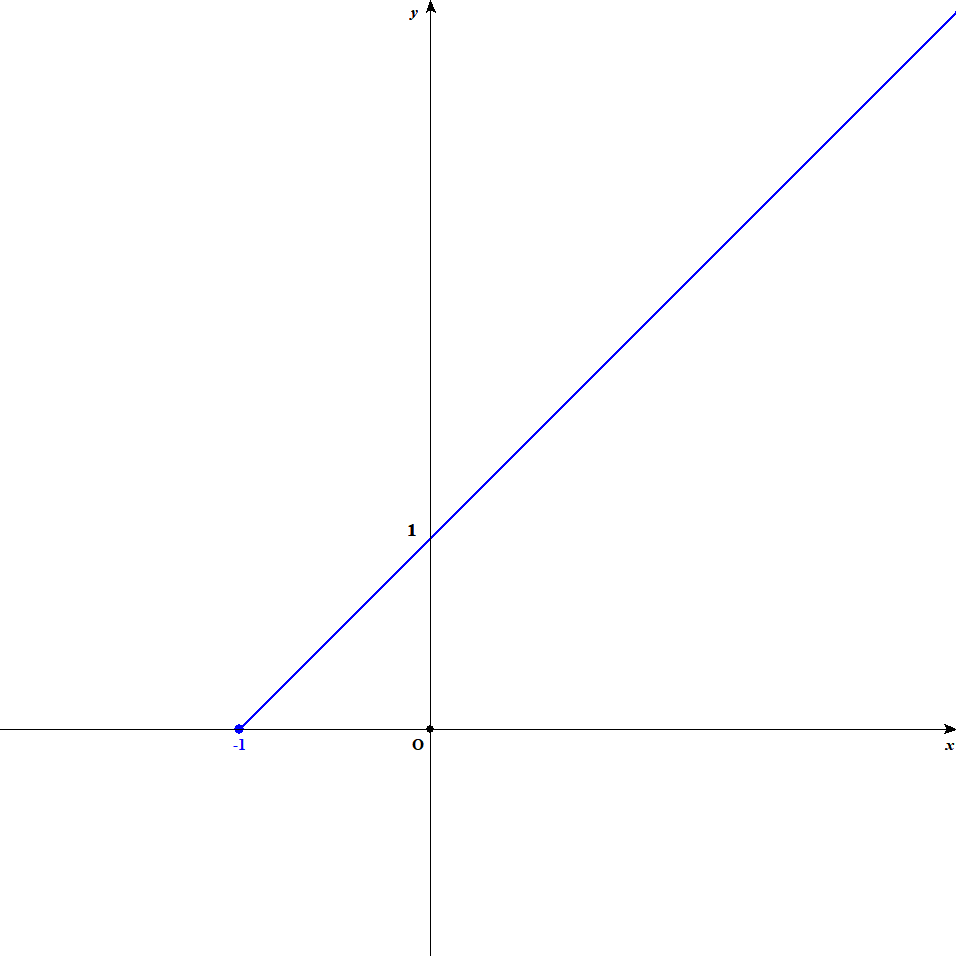
これも\(y = x + 1\)のグラフですが，定義域が\(-1 \leqq x\)になっています。 見ての通り，この関数はいくらでも大きな値をとりますから，最も大きい値というものは存在しません。 つまり，この関数にも最大値はありません。

確認問題

▲

次の関数\(f(x)\)について，\(f(2)\)を求めてください。

  1. \(f(x) = x^3 - x\)

  2. \(f(x) = x^2 + 2^x\)

  3. \(f(x) = \displaystyle\frac{x - 1}{x^2 + 2}\)

答え

\(x = 2\)を代入して計算するだけですね。

  1. \(f(2) = 2^3 -2 = \)\(6\)

  2. \(f(2) = 2^2 + 2^2 = \)\(8\)

  3. \(f(2) = \displaystyle\frac{2 - 1}{2^2 + 2} = \)\(\displaystyle\frac{1}{6}\)

次の関数の値域を求めてください。

  1. \(y = 2x \quad (-1 \leqq x < 4)\)

  2. \(y = -3x - 2 \quad (2 < x < 3)\)

  3. \(y = -\displaystyle\frac{2}{x} \quad (-3 \leqq x \leqq -1)\)

答え

この問題の関数は，定義域内で常に減少するか増加しています。 なので，定義域の端の値を調べれば値域が分かります。 もちろんグラフをかいて確認してもＯＫです。

問題の関数をすべて\(f(x)\)とおきます。

  1. この関数は定義域内で常に増加します。 よって，値域は\(f(-1) \leqq y < f(4)\)となります。 計算すると，\(-2 \leqq y < 8\)が値域です。 グラフは以下のようになっています。

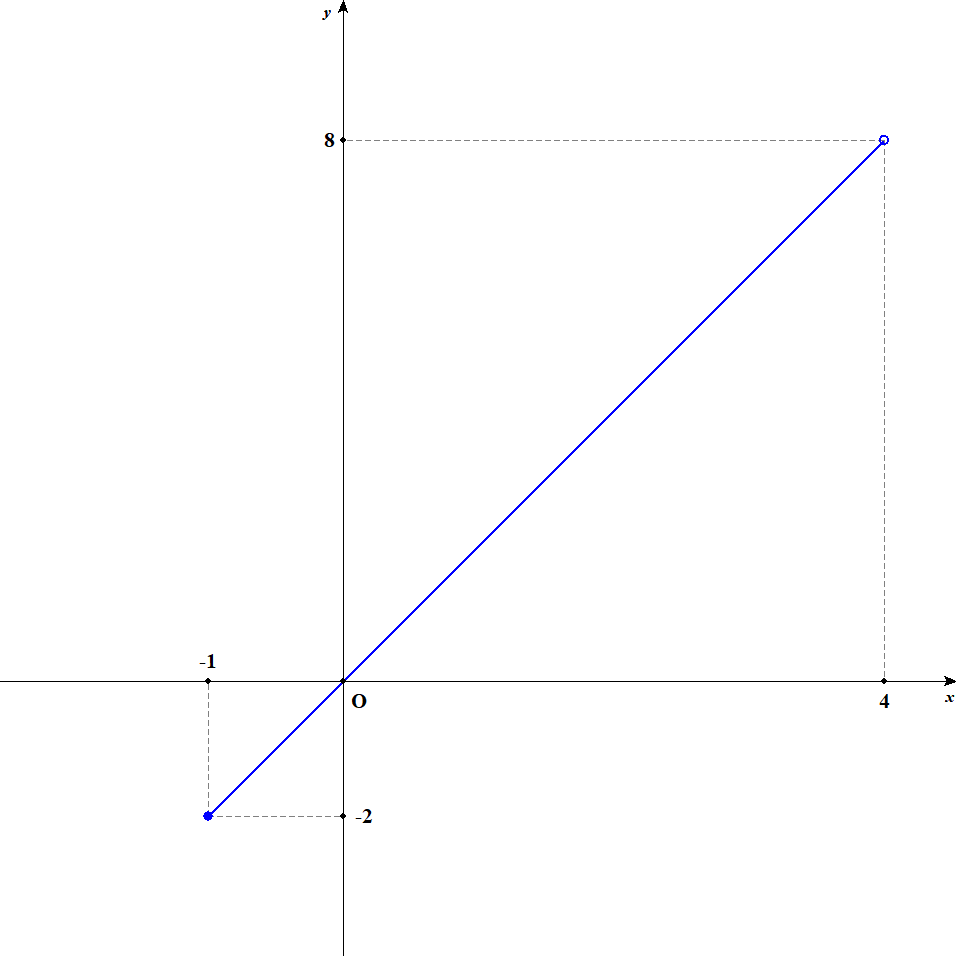
  2. この関数は定義域内で常に減少します。 よって，値域は\(f(3) < y < f(2)\)となります。 計算すると，\(-11 < y < -8\)が値域です。 グラフは以下のようになっています。

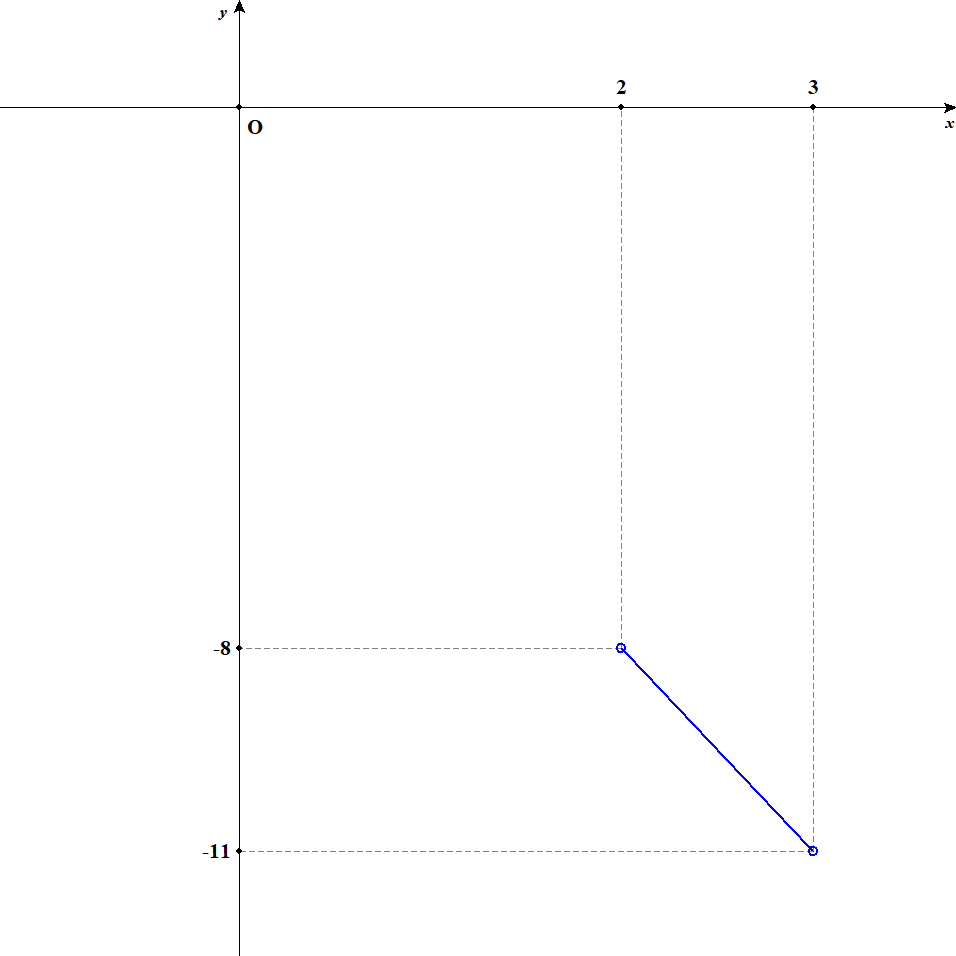
  3. この関数は定義域内で常に増加します。 よって，値域は\(f(-3) \leqq y \leqq f(-1)\)となります。 計算すると，\(\displaystyle\frac{2}{3} \leqq y \leqq 2\)が値域です。 グラフは以下のようになっています。

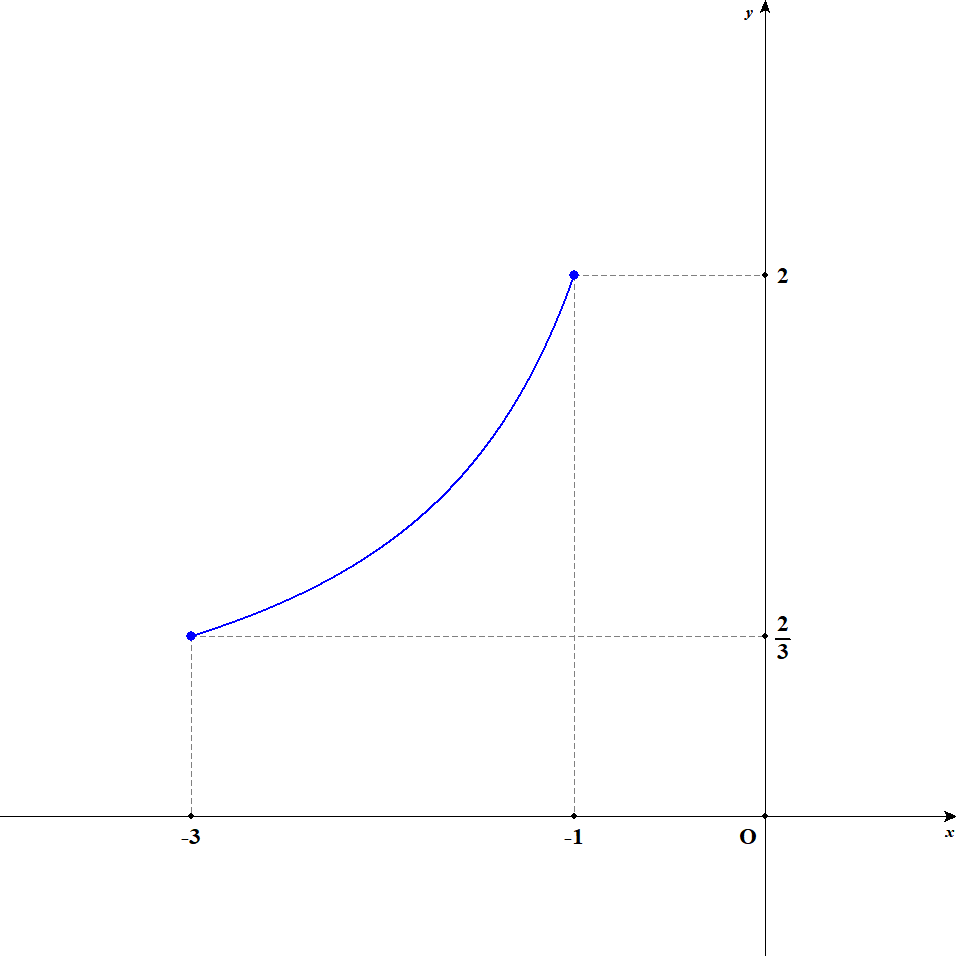
次の関数のグラフをかいてください。

  1. \(y = 2x - 2\)

  2. \(y = -2x + 4 \quad (-1 \leqq x \leqq 2)\)

  3. \(x = -1\)

  4. \(y = 2\)

答え

どれも直線のグラフです。 \(x\)切片と\(y\)切片の座標を明記するようにしましょう。 \(x = 0\)を代入して\(y\)を求めれば\(y\)切片が，\(y = 0\)を代入して\(x\)を求めれば\(x\)切片が得られます。

(3)と(4)は常に一定値をとる定数関数です。 これは常に同じ値をとりますから，座標を明記するのは\(x\)切片または\(y\)切片のひとつだけで構いません。

  1. グラフは以下の通りになります。 \(x\)切片と\(y\)切片の座標を明記します。

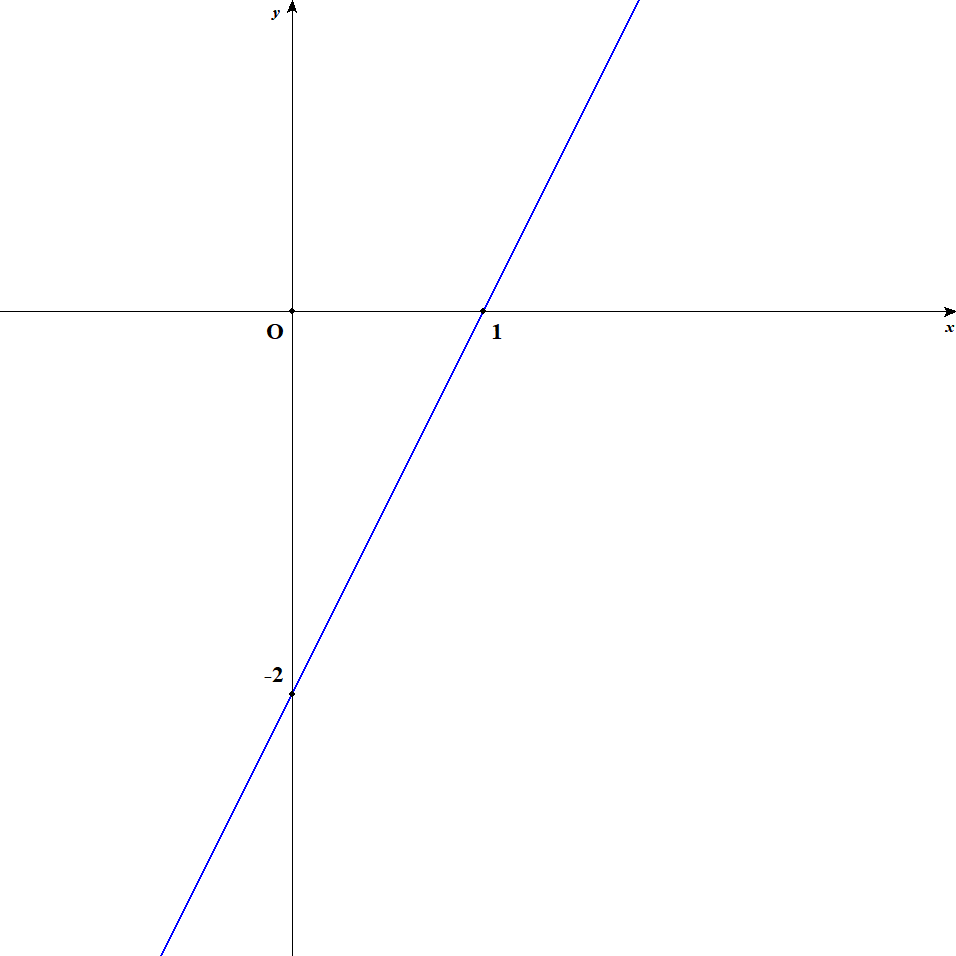
  2. グラフは以下の通りになります。 \(x\)切片と\(y\)切片の座標を明記します。 また，定義域の端の座標も分かるようにしておきます。

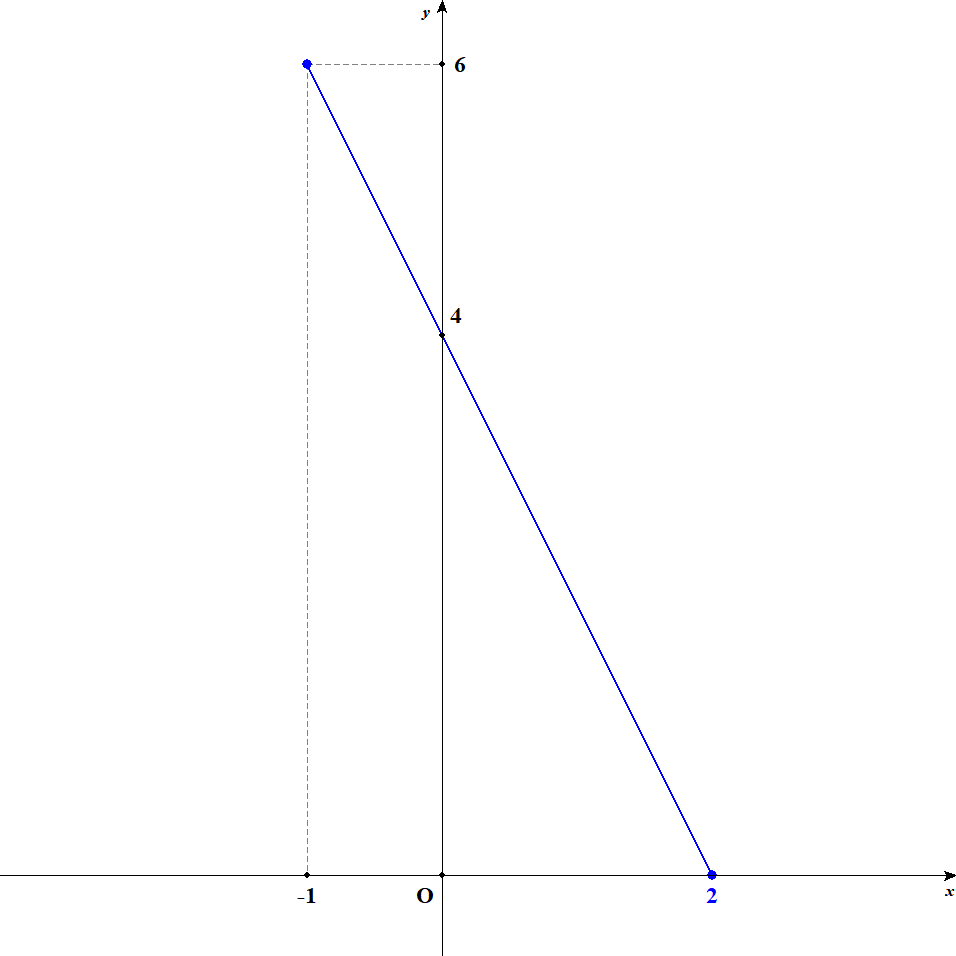
  3. グラフは以下の通りになります。 \(x\)切片の座標を明記します。 \(y\)に関わらず\(x\)の値が常に決まっているので，こんなグラフになります。

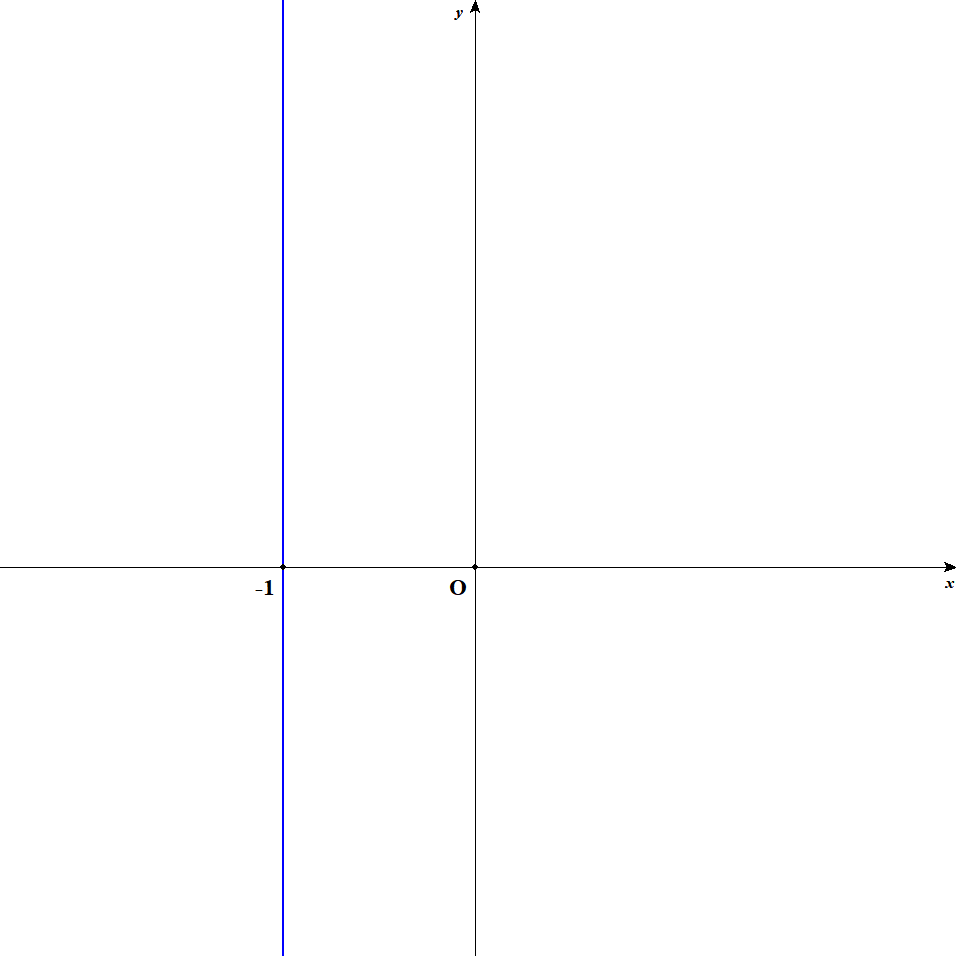
  4. グラフは以下の通りになります。 \(y\)切片の座標を明記します。 \(x\)に関わらず\(y\)の値が常に決まっているので，こんなグラフになります。

次の関数の最大値・最小値を求めてください。

  1. \(y = x \quad (-1 \leqq x \leqq 1)\)

  2. \(y = -2x + 1 \quad (x > 0)\)

  3. \(y = x + 2 \quad (x \leqq 2)\)

答え

グラフをかかなくても最大値・最小値を考えられますが，ここではグラフをかいて考えましょう。

  1. まず，問題の関数のグラフは次のようになります。

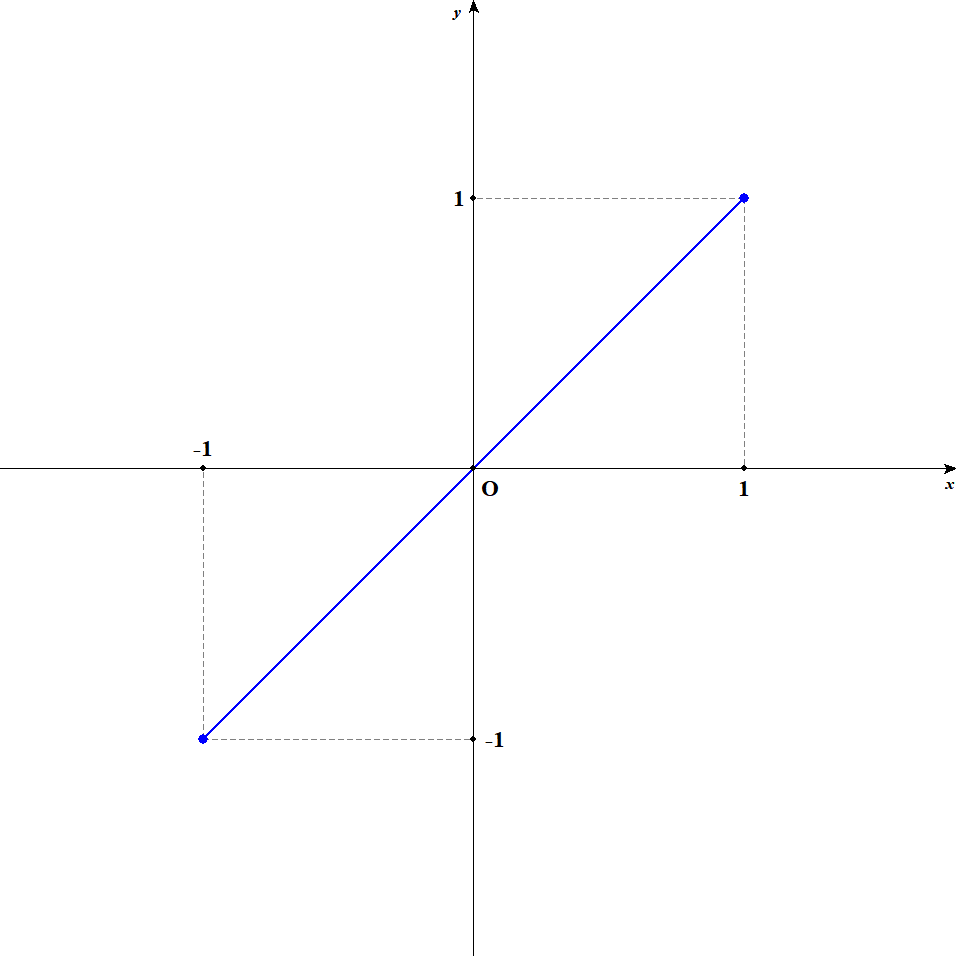
    グラフを見れば，\(x = 1\)のとき最大値\(1\)，\(x = -1\)のとき最小値\(-1\)をとることが分かります。

  2. まず，問題の関数のグラフは次のようになります。

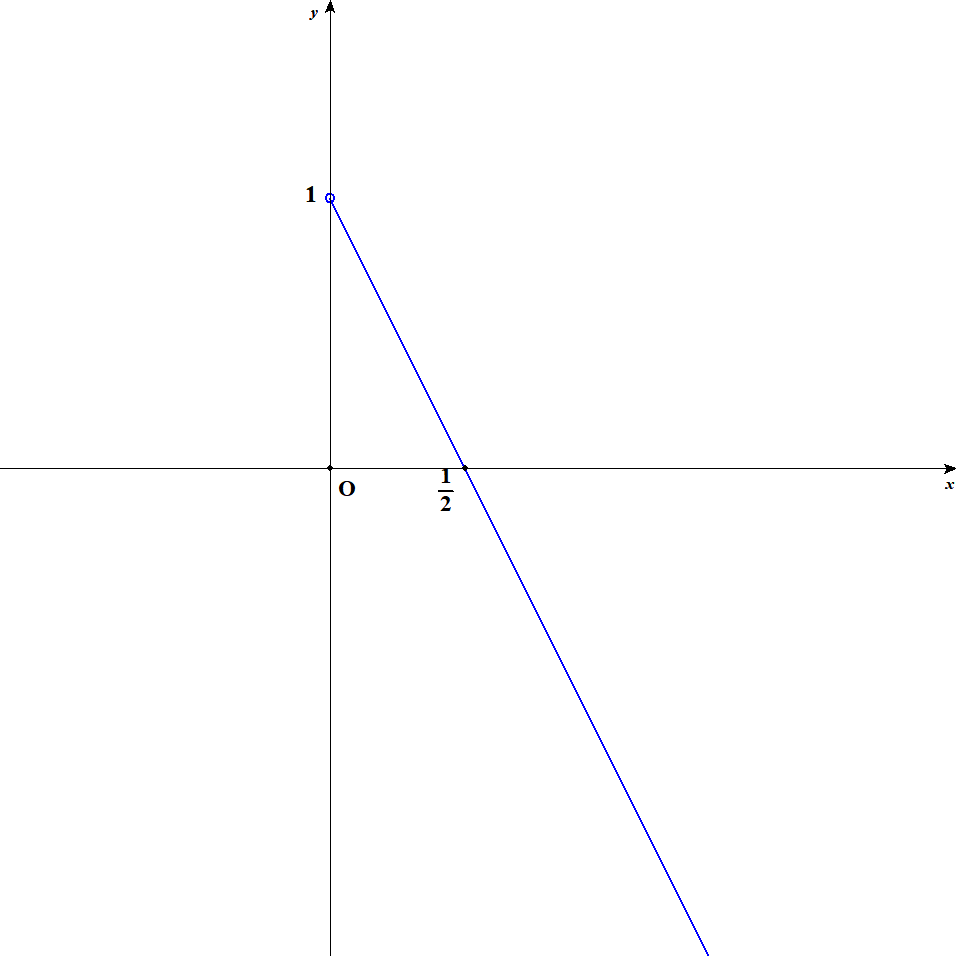
    グラフを見れば，最大値も最小値もないことが分かります。 一見\(x = 0\)で最大値をとりそうですが，\(x = 0\)は定義域に含まれないのでダメです。 最小値については，この関数がいくらでも小さい値をとれるので存在しません。

  3. まず，問題の関数のグラフは次のようになります。

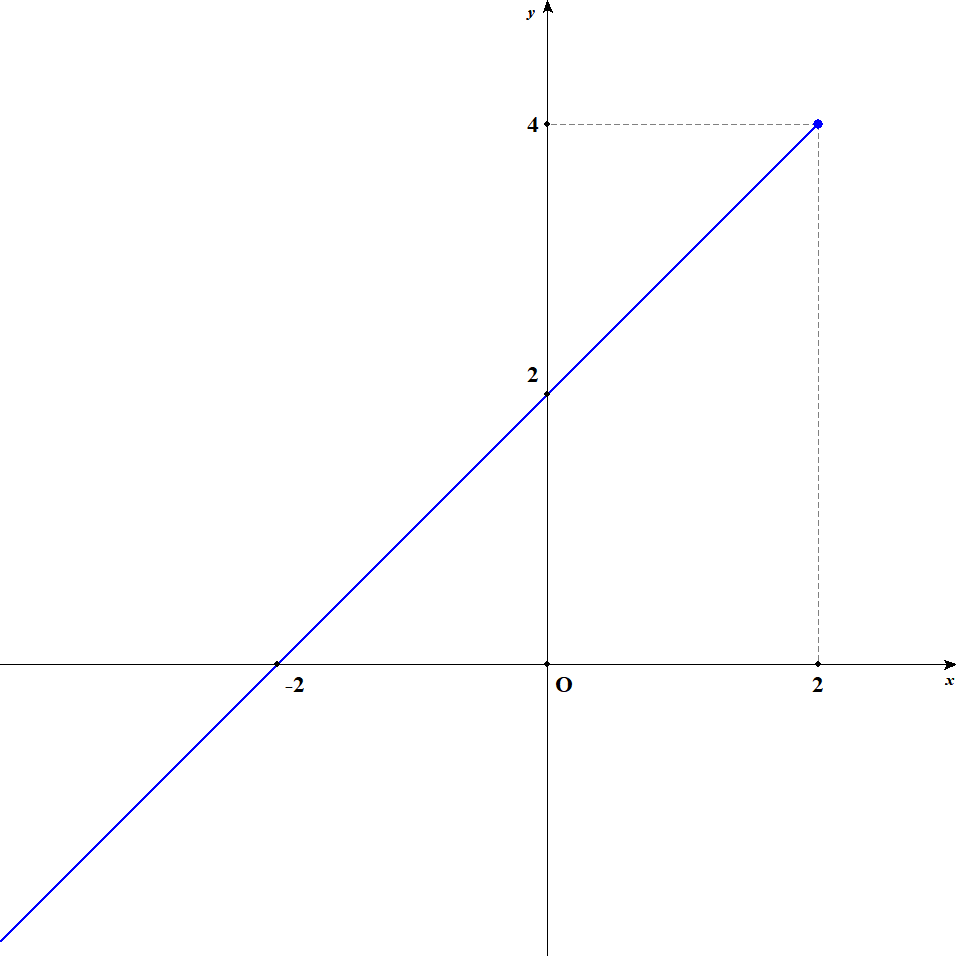
    グラフを見れば，\(x = 2\)のとき最大値\(4\)をとり，最小値はないことが分かります。 最小値については，この関数がいくらでも小さい値をとれるので存在しません。

あなたは今，高い塔の上にいて，そこから鉄球を真下に投げつけようとしています。 鉄球を\(v_o\)[m/s]の速さで投げ下ろすと，重力によって加速していき，\(t\)秒後には鉄球は\(4.9t^2 + v_o t\)[m]の距離を落下します。 ただし，この塔はあまりに高いので，鉄球が地面に到達することはありません。

  1. 鉄球を\(3\)[m/s]の速さで投げ下ろしたとき，鉄球が落下する距離\(h\)[m]を\(t\)の関数として表してください。

  2. 鉄球を投げ下ろしてから\(10\)秒間で鉄球が落下する距離\(h\)[m]を\(v_o\)の関数として表してください。

答え

\(v_o\)や\(t\)に指定の値を代入するだけです。 \(4.9t^2 + v_o t\)は\(v_o, t\)という変数を持つ２変数関数ですが，片方の変数の値を固定するとき，１変数関数になります。

\(f(v_o, t) = 4.9t^2 + v_o t\)とおきます。

  1. 問題の仮定から\(v_o = 3\)ですから，\(h = f(3, t)\)です。 よって，\(h = 4.9t^2 + 3t\)です。

  2. 問題の仮定から\(t = 10\)ですから，\(h = f(v_o, 10)\)です。 よって，\(h = 10v_o + 490\)です。

次の関数のグラフをかいて，最大値・最小値を求めてください。

\(y = \vert x - 1 \vert + 1\)

答え

式に絶対値が含まれているので，場合分けをして絶対値を外しましょう。 関数は\(x < 1\)のとき\(y = -(x - 1) + 1 = -x + 2\)，\(x \geqq 1\)のとき\(y = (x - 1) + 1 = x\)です。 よって，\(x < 1\)を定義域とする関数\(y = -x + 2\)と，\(x \geqq 1\)を定義域とする関数\(y = x\)のグラフを一緒にかけばＯＫです。

グラフは下図の実線部分のようになります。

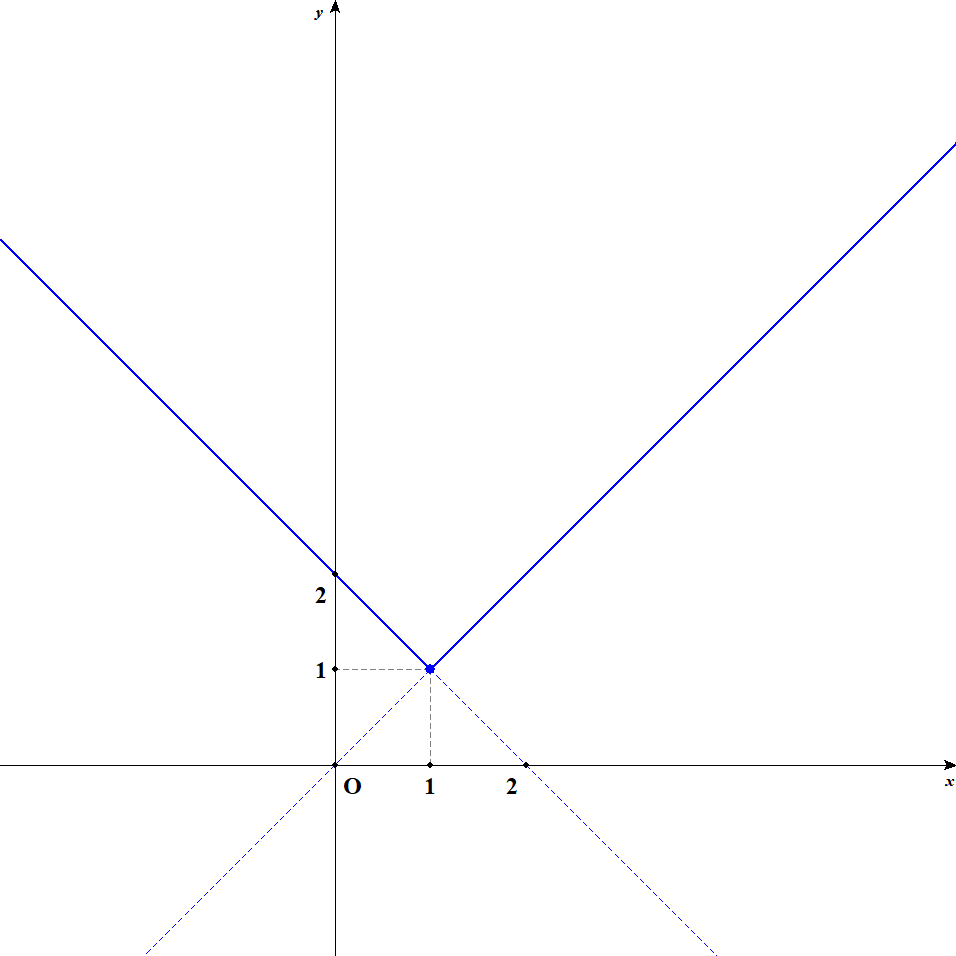
グラフを見れば，\(x = 1\)のとき最小値\(1\)をとり，最大値はないことが分かります。 最大値については，この関数がいくらでも大きい値をとれるので存在しません。