2次関数の簡単な応用例は,投射物の運動の記述です。 また,複雑な現象を2次関数で近似するということも行われます。 2次関数は扱いやすい関数ですが,応用範囲が広いのです。
目次
2次関数とグラフ
2次関数は2次式で表される関数です。 つまり,2次関数は3つの定数\(a, b, c\)を用いて次のように表せます。 ただし,\(a \neq 0\)です。(\(a = 0\)だと2次式じゃなくなります。)
ではさっそく2次関数のグラフを見ていきましょう。 最もシンプルな\(y = x^2\)のグラフは次のようになります。
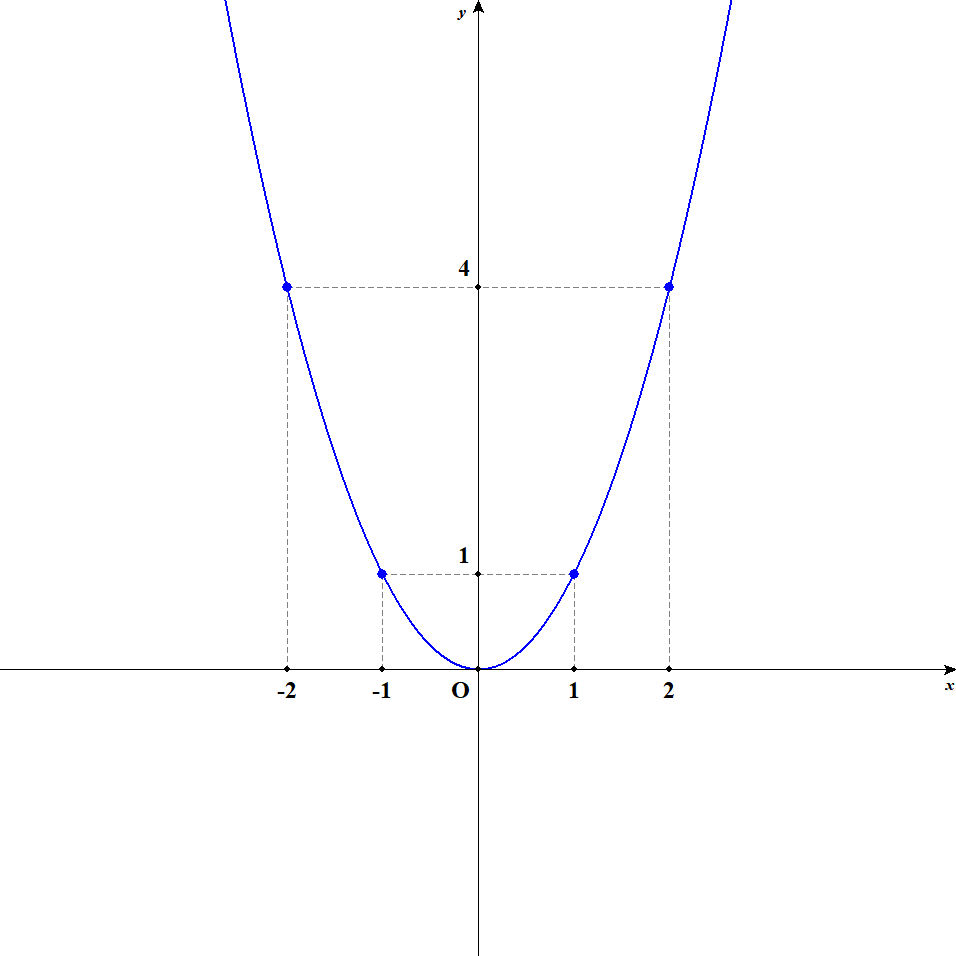
これは中学でも習うグラフですね。 このグラフのように,2次関数のグラフは放物線になっています。 また,\(y = ax^2 + bx + c\)を放物線の方程式ともいいます。
放物線はその名の通り,(空気抵抗などを無視した場合の話ですが)物を放り投げたときの軌道になっています。 詳しくは物理学で学びますが,今後,確認問題にも少し載せます。
\(y = ax^2 + bx + c\)の\(a\)の部分はグラフの形状に関わる部分です。 簡単な例として,\(y = x^2\),\(y = 5x^2\),\(y = -x^2\),\(y = -5x^2\)のグラフを見比べてみましょう。 下図を見てください。
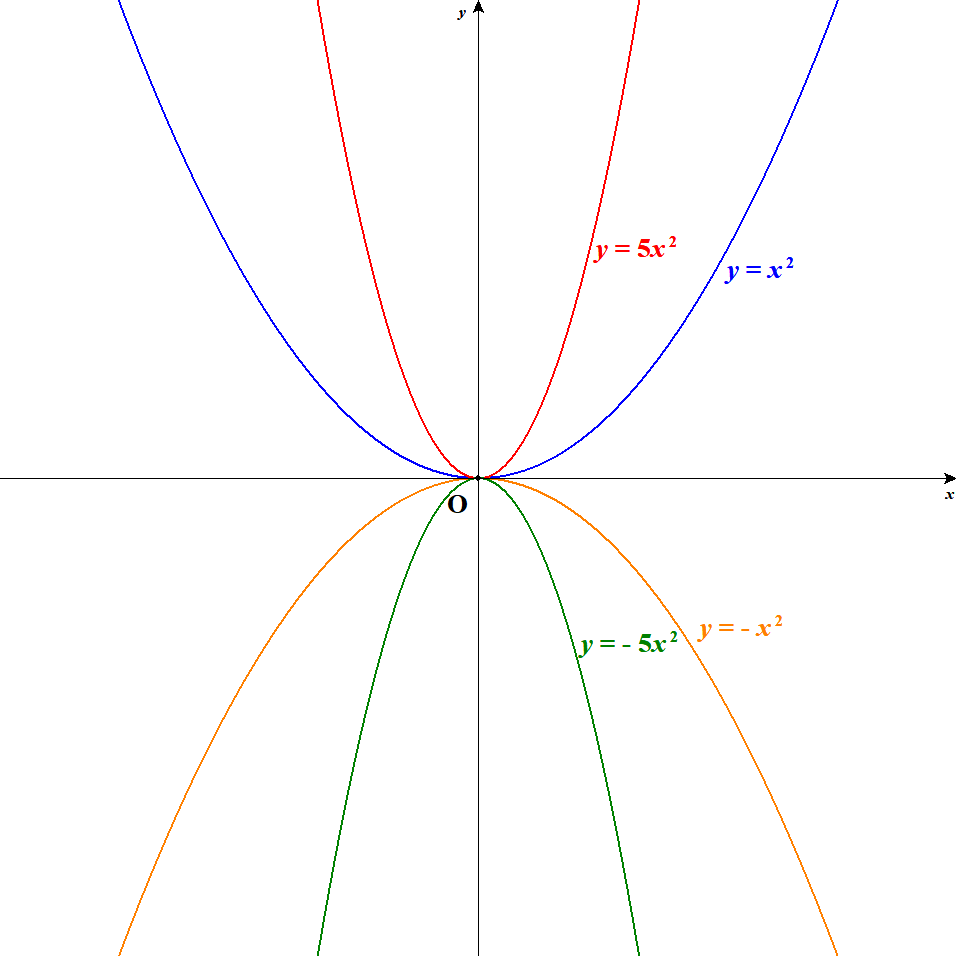
グラフを見ると,2つのことに気が付きます。
ひとつは,\(a\)が正のとき放物線の先端が下向きで,負の時は上向きになっていることです。 放物線が下向き(\(a > 0\))のとき下に凸,上向き(\(a < 0\))のとき上に凸といいます。
もうひとつは,\(a\)の絶対値が大きいほど放物線の開き具合が小さい(よりとがっている)ことです。 これは,\(a\)の絶対値が大きいとその分,関数の値の変化が急激になるからです。
\(y = ax^2 + bx + c\)の\(a\)は放物線の形状に影響しました。 では\(b, c\)は何に影響するのかというと,(\(a\)もですが)放物線の位置に影響します。 放物線の位置は,その頂点や軸で表すことができます。 次項で学びましょう。
頂点と軸
放物線には頂点と軸があります。 下図の通り,頂点は放物線の先端,軸は放物線の真ん中を通る直線です。 もう少しちゃんと言うと,軸は放物線の対象軸,頂点は軸と放物線の交点です。
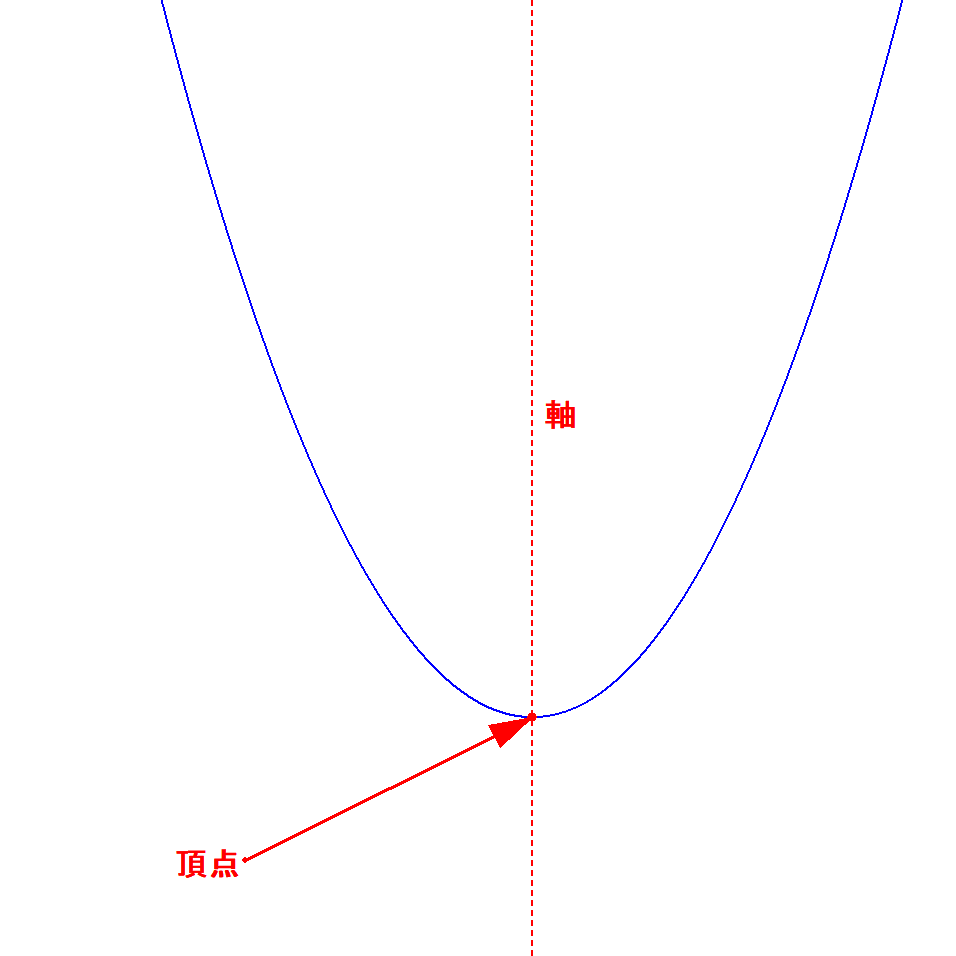
中学数学では,放物線の頂点は原点にありましたが,これからは頂点が原点にない放物線も扱います。 次の2次関数のグラフは,頂点が点\((p, q)\)である放物線になります。
逆に言えば,2次関数のグラフの頂点がどこにあるのかは,上のように式変形すれば分かります。 その式変形が次項で学ぶ平方完成です。
どうして\(y = a(x - p)^2 + q\)のグラフの頂点が点\((p, q)\)なのかは,次回学ぶ平行移動によって理解できます。 \(y = a(x - p)^2 + q\)は\(y = ax^2\)を平行移動したものなのです。
2次関数のグラフをかくときは,必ず頂点の座標と\(y\)切片の座標は明記するようにしましょう。 \(x\)切片の座標も明記した方が良いですが,後で学ぶ2次方程式を解く必要があるので,しばらくおあずけです。
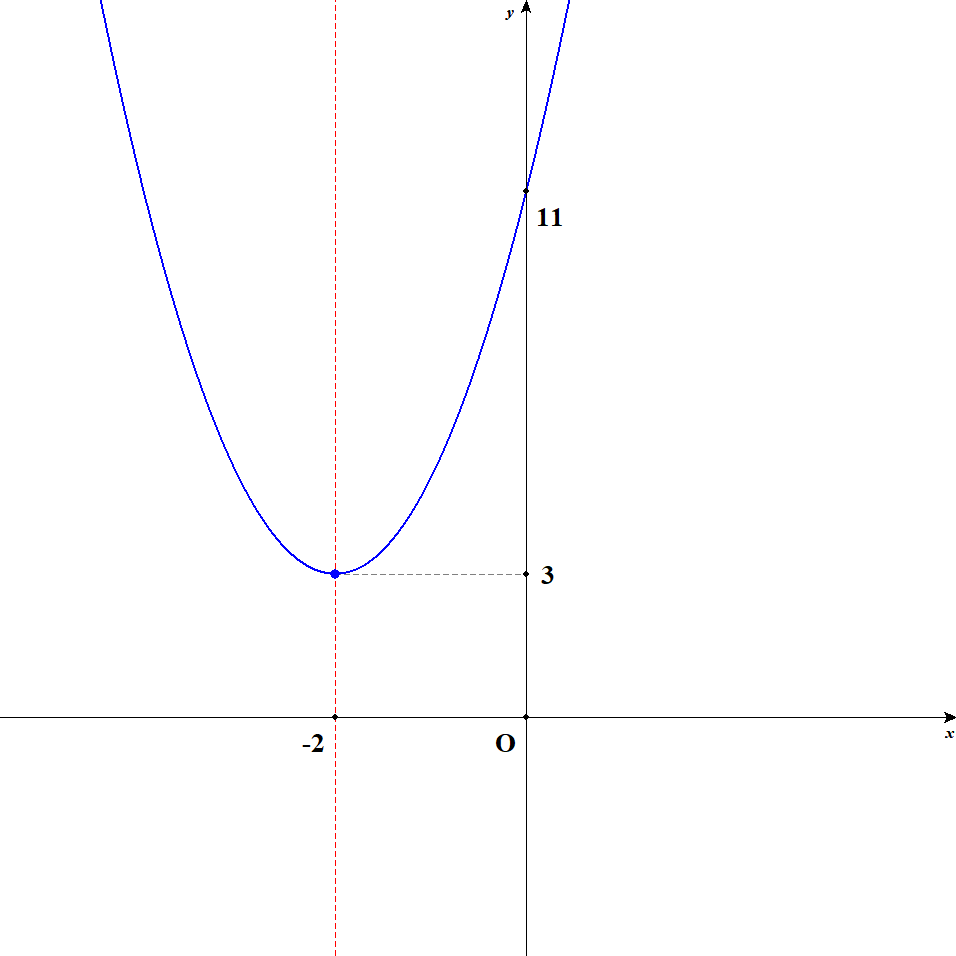
ひとつ例を見ておきましょう。 \(y = 2(x + 2)^2 + 3\)のグラフは次のようになります。 頂点が点\((-2, 3)\),軸が直線\(x = -2\)になっていることが分かりますね。
上の関数は\(y = 2\{x - (-2)\}^2 + 3\)と変形すれば,\(y = (x - p)^2 + q\)と同じ形になります。 これで頂点が点\((-2, 3)\)であると分かります。
平方完成
2次関数が\(y = a(x - p)^2 + q\)の形で書かれていれば,放物線の頂点や軸が分かります。 この形になっていない2次関数についても,この形に式変形してやれば,放物線の頂点や軸を知ることができます。 そのような式変形を平方完成といいます。
例として,\(y = x^2 + 4x + 1\)を平方完成して,放物線の頂点と軸を求めてみましょう。 平方完成の目標は,とにかく\(x\)の式の2乗を作ることです。
なので,まずは\(x\)の1次式の2乗の公式を復習しておきます。 次の公式だけ確認しておけば十分でしょう。
- \((x + a)^2 = x^2 + 2ax + a^2\)
- \((x - a)^2 = x^2 - 2ax + a^2\)
これから,この公式の右辺から左辺への式変形をしていきます。 ここで注目したいのが,\(x\)の係数です。 右辺の\(x\)の係数は\(2a\)ですが,左辺にはその半分である\(a\)が現れますね。
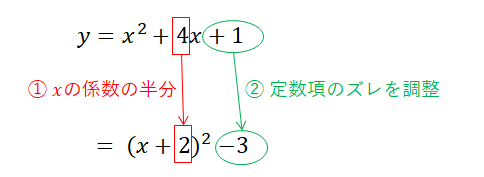
\(y = x^2 + 4x + 1\)では,\(x\)の係数は\(4\)で,その半分は\(2\)です。 なので,まずは\((x + 2)^2\)を使うことが分かります。 しかし,これをそのまま展開すると\(x^2 + 4x + 4\)となり,関数の式とは定数項が違いますね。
ここまできたら後は簡単です。 定数項のズレを調整すれば良いのです。 \((x + 2)^2\)を展開して出てくる余計な定数項\(4\)を追い払って,元の関数の定数項を使えばOKです。
これで,この関数のグラフが,点\((-2, -3)\)を頂点,直線\(x = -2\)を軸とする放物線であることが分かりました。
以上をまとめると,平方完成は次の2ステップです。
- \(x\)の係数の半分で2乗を作る
- 定数項のズレを調整する
もうひとつ,\(x^2\)の係数が\(1\)じゃない場合も確認しましょう。 この場合も「定数項のズレを後で直す」方針は変わりませんが,\(x\)の係数はそのまま使えません。 次の例を見てください。
このように,\(x^2\)の係数が\(1\)じゃない場合は,むりやり\(1\)にして考えます。 そのために,上式では\(x^2\)の係数で定数項以外の項をくくっています。 定数項はどうせ後で調整するので,一緒にくくりませんでした。
あとは平方完成の2ステップを使うだけですね。
確認問題
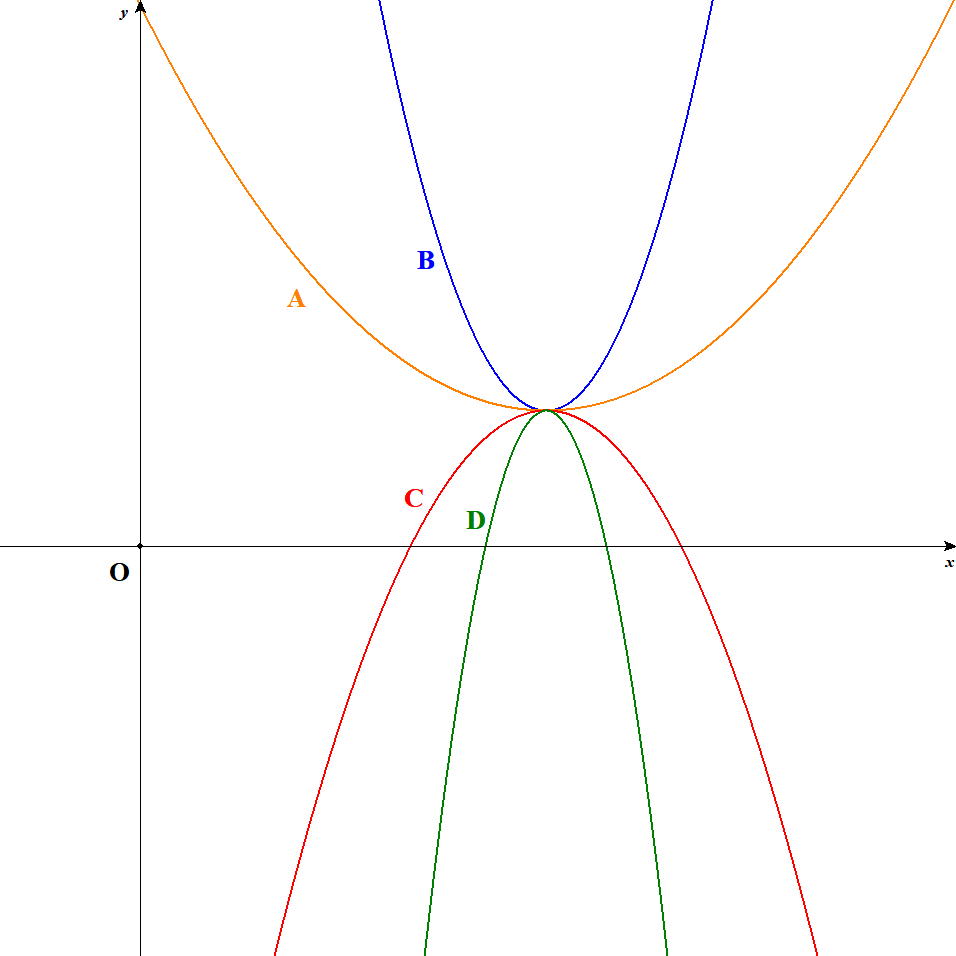
次の図には,以下の4つの関数のグラフが描かれています。 どのグラフがどの関数のものか,それぞれグラフ中の記号A~Dのうちから答えてください。
-
\(y = 2x^2 -12x + 19\)
-
\(y = \displaystyle\frac{1}{3}x^2 -2x + 4\)
-
\(y = -x^2 + 6x - 8\)
-
\(y = -5x^2 + 30x - 44\)
答え
図を見ると,4つの放物線の頂点は同じです。 異なるのは,下に凸か上に凸か,また放物線の開き具合が大きいか小さいかです。 これらを比較するには,\(x^2\)の係数だけみれば十分ですね。 平方完成などは一切必要ありません。
(1)と(2)の関数は,\(x^2\)の係数が正ですから,グラフは下に凸です。 よって,それぞれAかBのいずれかですね。
(3)と(4)の関数は,\(x^2\)の係数が負ですから,グラフは上に凸です。 よって,それぞれCかDのいずれかですね。
-
同じく下に凸の(2)と比べると,\(x^2\)の係数の絶対値が大きいです。 よって,グラフはより開き具合が小さいBの方です。
-
同じく下に凸の(1)と比べると,\(x^2\)の係数の絶対値が小さいです。 よって,グラフはより開き具合が大きいAの方です。
-
同じく上に凸の(4)と比べると,\(x^2\)の係数の絶対値が小さいです。 よって,グラフはより開き具合が大きいCの方です。
-
同じく上に凸の(3)と比べると,\(x^2\)の係数の絶対値が大きいです。 よって,グラフはより開き具合が小さいDの方です。
次の関数のグラフは放物線になりますが,その頂点の座標を求めてください。
-
\(y = x^2 + 8x - 4\)
-
\(y = x^2 - 5x\)
-
\(y = -x^2 + 2x + 5\)
-
\(y = 3x^2 - x + 1\)
答え
平方完成して\(a(x - p)^2 + q\)の形に変形しましょう。 \(x\)の係数の半分を使って2乗を作り,定数項を調整します。
-
関数式を平方完成すると,以下のようになります。
\( \begin{align} & \quad \ x^2 + 8x - 4 \\[5pt] &= (x + 4)^2 - 16 - 4 \\[5pt] &= (x + 4)^2 - 20 \end{align} \)よって,頂点の座標は\((-4, -20)\)です。
-
関数式を平方完成すると,以下のようになります。
\( \begin{align} & \quad \ x^2 - 5x \\[5pt] &= \left(x - \displaystyle\frac{5}{2}\right)^2 - \displaystyle\frac{25}{4} \end{align} \)よって,頂点の座標は\(\left(\displaystyle\frac{5}{2}, -\displaystyle\frac{25}{4}\right)\)です。
-
関数式を平方完成すると,以下のようになります。
\( \begin{align} & \quad \ -x^2 + 2x + 5 \\[5pt] &= -(x^2 - 2x) + 5 \\[5pt] &= -\{(x - 1)^2 - 1\} + 5 \\[5pt] &= -(x - 1)^2 + 6 \end{align} \)よって,頂点の座標は\((1, 6)\)です。
-
関数式を平方完成すると,以下のようになります。
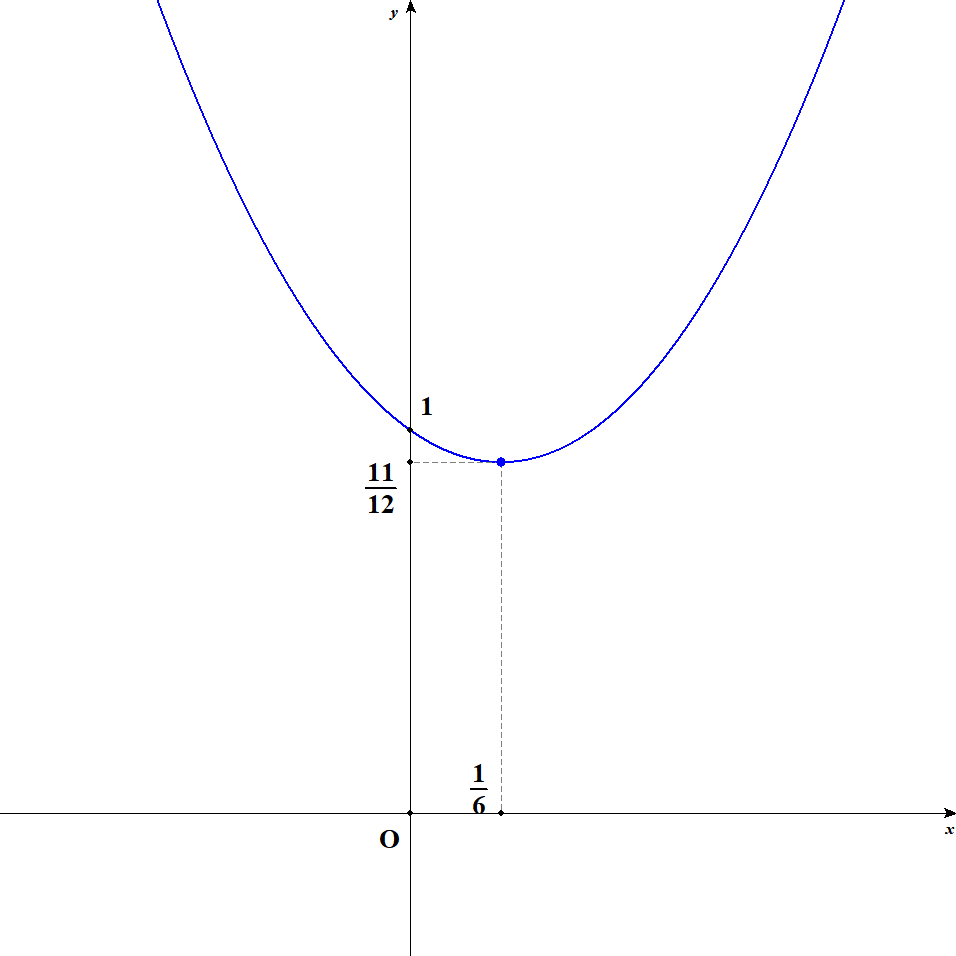
\( \begin{align} & \quad \ 3x^2 - x + 1 \\[5pt] &= 3\left(x^2 - \displaystyle\frac{1}{3}x\right) + 1 \\[5pt] &= 3\left\{\left(x - \displaystyle\frac{1}{6}\right)^2 - \displaystyle\frac{1}{36}\right\} + 1 \\[5pt] &= 3\left(x - \displaystyle\frac{1}{6}\right)^2 + \displaystyle\frac{11}{12} \end{align} \)よって,頂点の座標は\(\left(\displaystyle\frac{1}{6}, \displaystyle\frac{11}{12}\right)\)です。
次の関数のグラフをかいてください。 関数は前問題と同じものです。
-
\(y = x^2 + 8x - 4\)
-
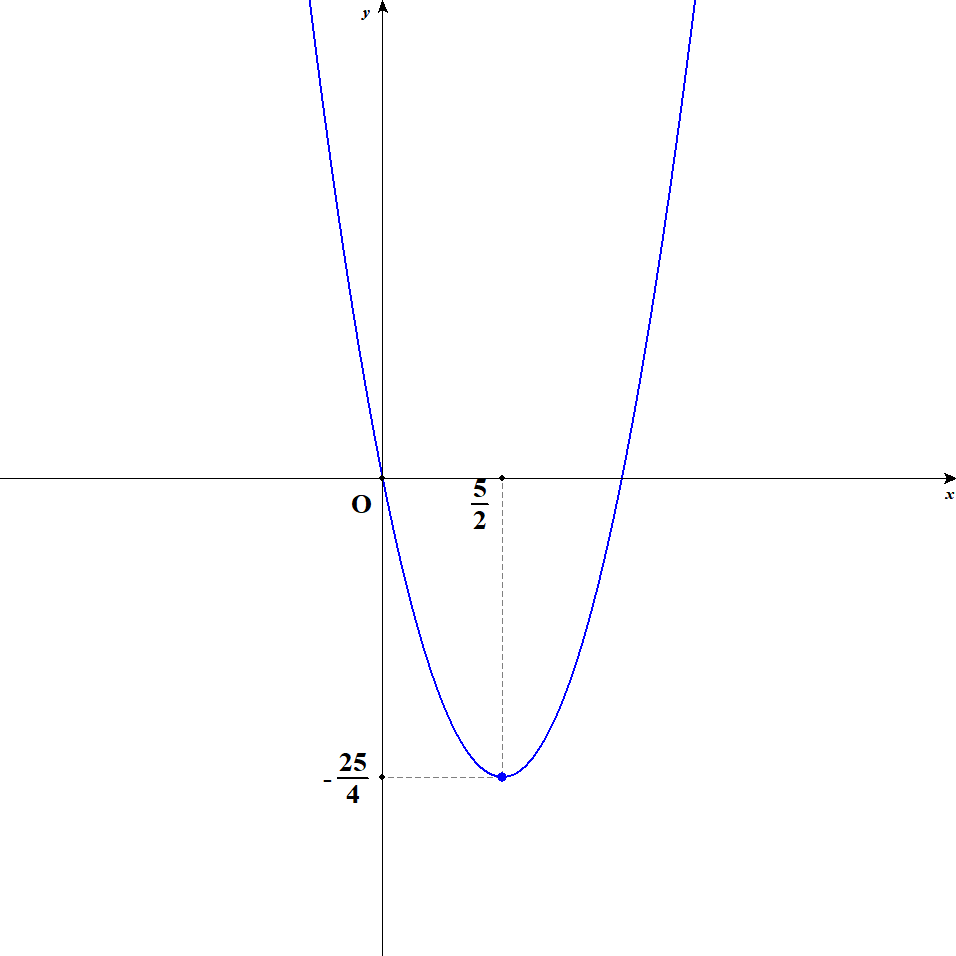
\(y = x^2 - 5x\)
-
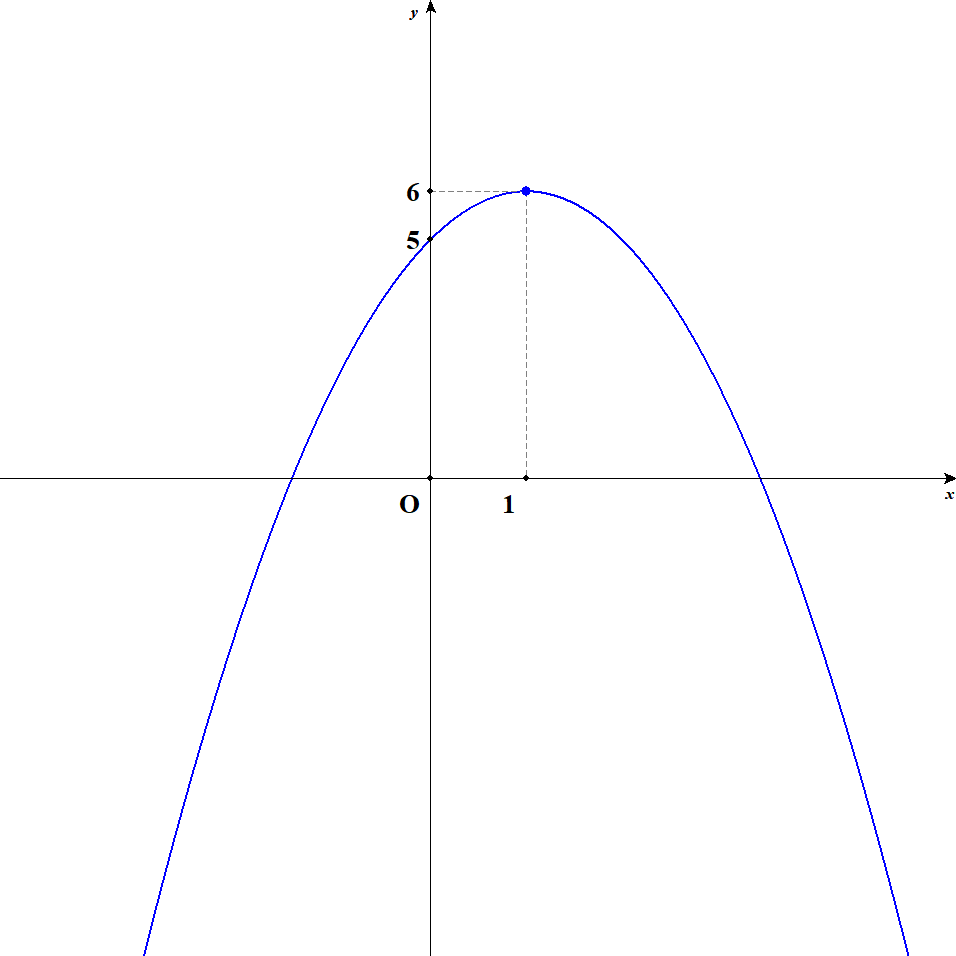
\(y = -x^2 + 2x + 5\)
-
\(y = 3x^2 - x + 1\)
答え
グラフの頂点は前問題で求めました。 あとは\(y\)切片の座標を求めて,放物線の形になるように滑らかに結びましょう。 \(y\)切片は関数式で\(x = 0\)とすれば求められますね。
-
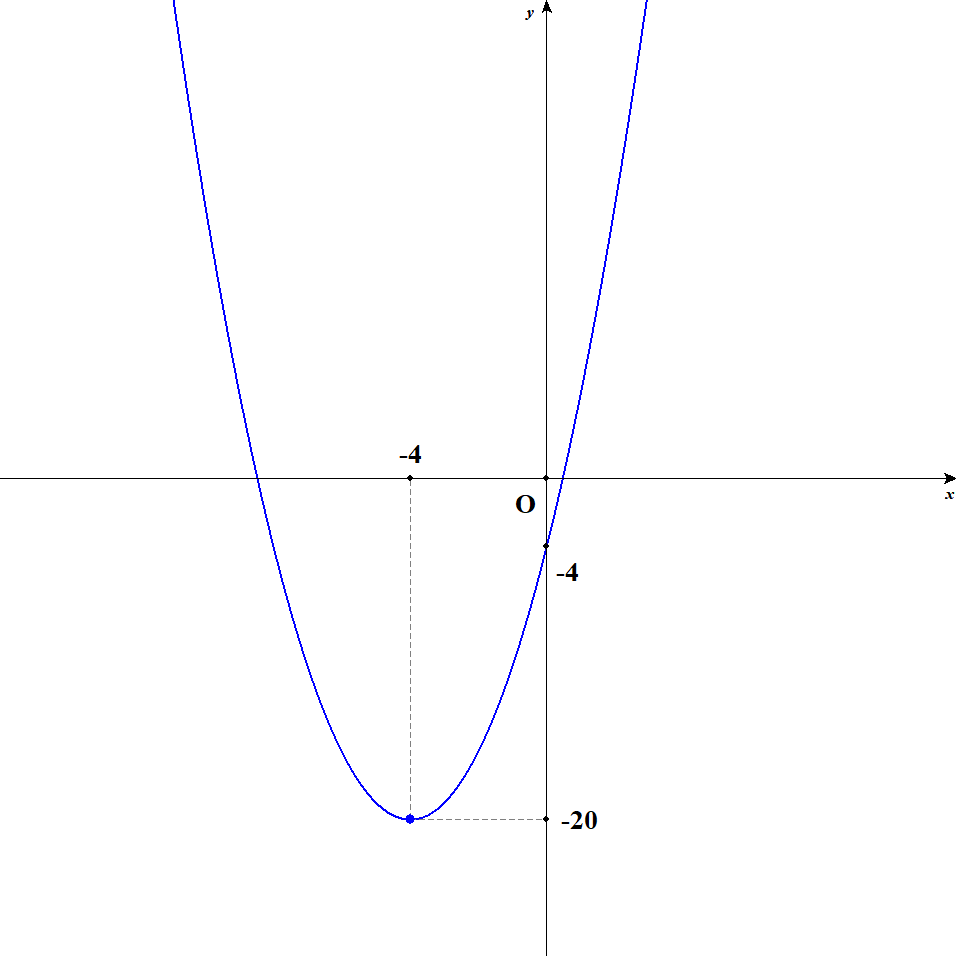
\(y\)切片の座標は,関数式で\(x = 0\)とすることで,\((0, -4)\)と求められます。 したがって,グラフは次のようになります。
-
\(y\)切片の座標は,関数式で\(x = 0\)とすることで,\((0, 0)\)と求められます。 したがって,グラフは次のようになります。
-
\(y\)切片の座標は,関数式で\(x = 0\)とすることで,\((0, 5)\)と求められます。 したがって,グラフは次のようになります。
-
\(y\)切片の座標は,関数式で\(x = 0\)とすることで,\((0, 1)\)と求められます。 したがって,グラフは次のようになります。