グラフは,大雑把に言えば,形状と位置によって決まります。 このうち形状については,1次関数は直線,2次関数は放物線というような知識が(今のところは)必要です。
しかし位置については,平行移動を理解すれば,どんな位置のものにも対応できます。 また,関数の移動には対称移動もあります。 併せて学びましょう。
目次
平行移動
前回学んだ通り,2次関数のグラフの形状は\(x^2\)の係数で決まります。 ということは,以下3つの関数のグラフも全く同じ形状なのです。
これらのグラフの違いは,グラフがどこにあるかという「位置」だけです。 放物線の位置は,頂点の座標で比較できますね。 頂点の座標を求めるための式変形が平方完成でした。
位置だけが違うグラフは,平行移動によって完全に同じものになります。 平行移動とは,グラフをスライドさせる移動方法です。 縮めたり伸ばしたり,ひっくり返したりはしません。 なので平行移動後のグラフは,元のグラフと合同です。

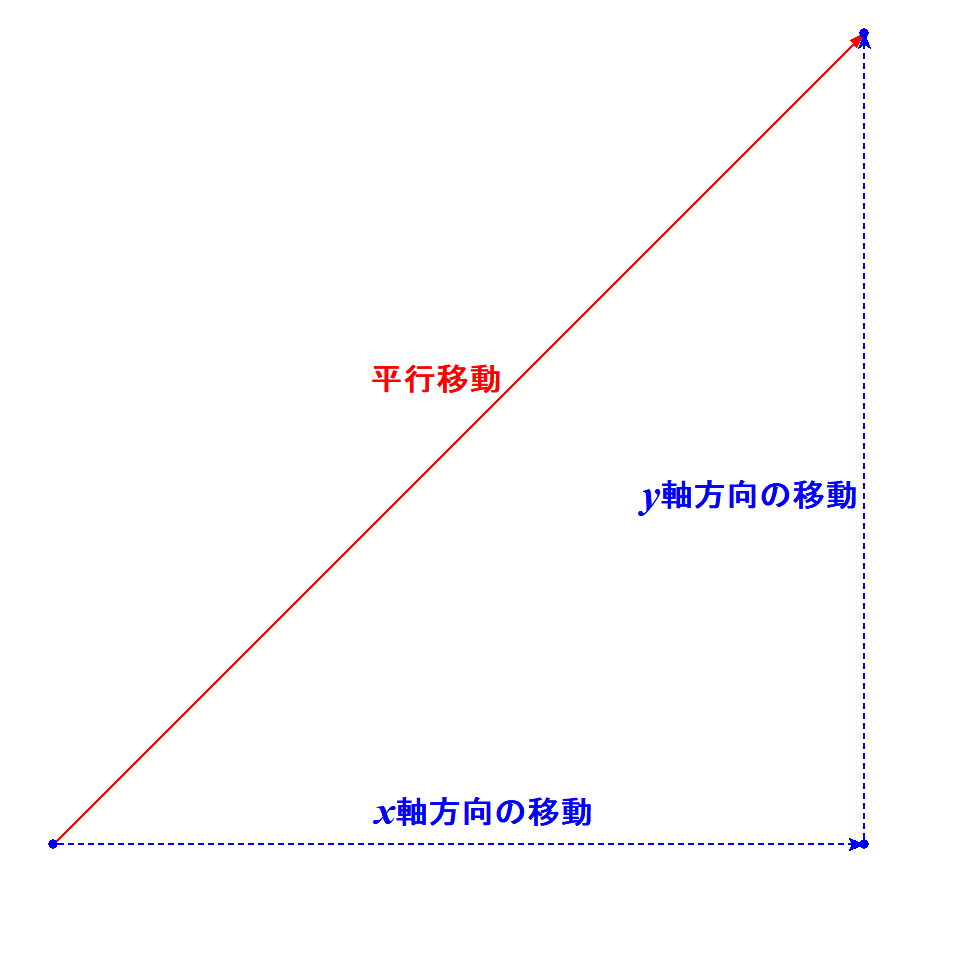
平行移動は\(x\)軸方向にどれだけ動いたかと,\(y\)軸方向にどれだけ動いたかで表現できます。
例えば,関数\(y = (x - 2)^2 + 1\)のグラフを\(x\)軸方向に\(-4\),\(y\)軸方向に\(2\)だけ平行移動すると,下図のようになります。 頂点の座標が\((2, 1)\)から\((-2, 3)\)に移ることが分かりますね。
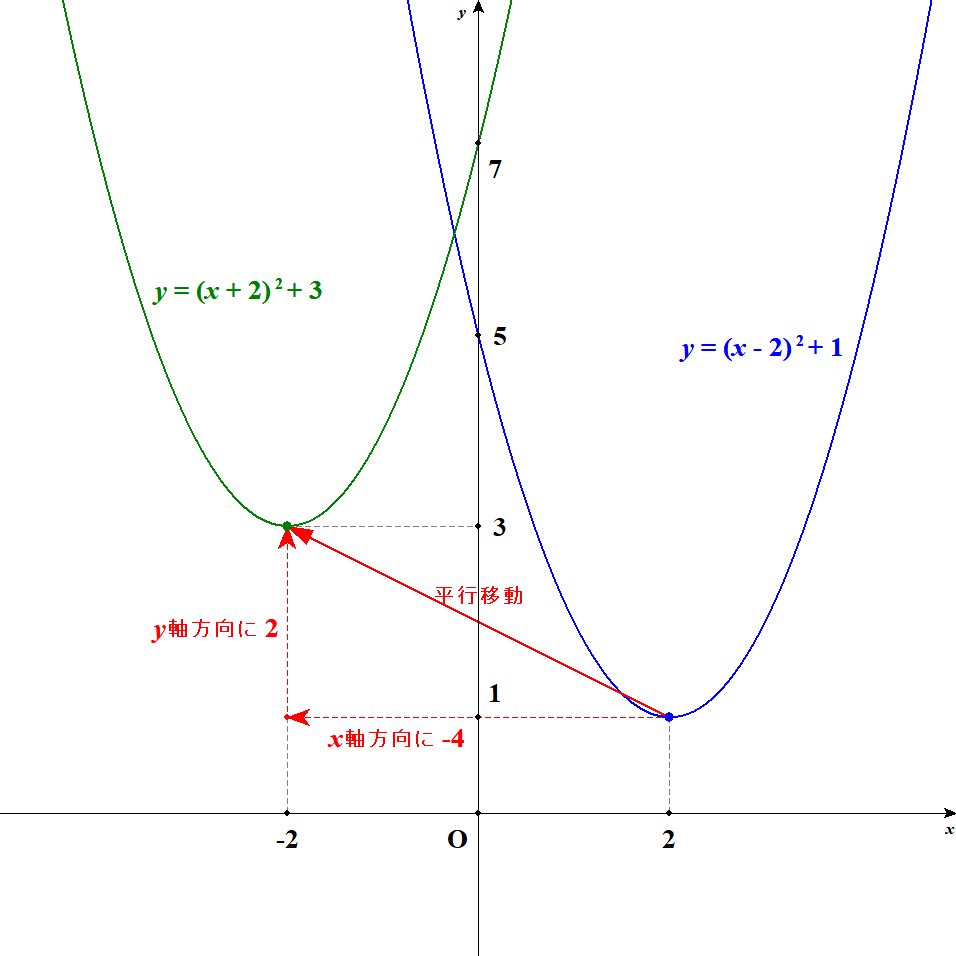
平行移動の意味が分かったところで,次は平行移動で関数式がどう変わるのかを確認しましょう。 結論からいうと,平行移動は,関数式を次のように変えることで実現できます。
関数\(y = f(x)\)のグラフを\(x\)軸方向に\(p\),\(y\)軸方向に\(q\)だけ移動したものの関数式は,次のようになる。
これは,元の関数式を\(x \rightarrow x - p\),\(y \rightarrow y - q\)と変更したものである。
例えば,放物線\(y = x^2 + 2x + 3\)を\(x\)軸方向に\(2\),\(y\)軸方向に\(-1\)だけ平行移動した放物線の方程式は次のようになります。
整理すると\(y = x^2 - 2x + 2\)になります。 頂点が\((-1, 2)\)から\((1, 1)\)に移っていることも確認してみてください。
平行移動の式変形について確認しておきます。 グラフ\(G\)の方程式が\(y = f(x)\)で,これを\(x\)軸方向に\(p\),\(y\)軸方向に\(q\)だけ平行移動したグラフを\(H\)とします。 \(H\)の方程式が\(y - q = f(x - p)\)になることを確認しましょう。
\(H\)上の点\((x, y)\)の\(x, y\)間の関係が分かれば,その方程式が得られます。 いま\(H\)について分かっていることは,\(G\)を平行移動したものだということです。 それはつまり,\(H\)上の点を逆向きに平行移動すれば,\(G\)上の点になるということです。
\(H\)上の点\((x, y)\)を\(x\)軸方向に\(-p\),\(y\)軸方向に\(-q\)だけ平行移動すれば,\(G\)上の点になります。 平行移動後の点\((x - p, y - q)\)は\(G\)の方程式を満たしますから,\(y - q = f(x - p)\)という関係式が得られます。 これは\(H\)上の点\((x, y)\)の\(x, y\)間の関係であり,\(H\)の方程式です。
対称移動
平行移動の他に重要なグラフの移動として,対称移動があります。 特に数学Ⅰで使うのは,「\(x\)軸に関して対称移動」「\(y\)軸に関して対称移動」「原点に関して対称移動」の3つです。
「\(x\)軸,\(y\)軸に関して対称移動」は,線対称移動です。 それぞれ\(x\)軸,\(y\)軸を対称軸とします。 「原点に関して対称移動」は,原点を回転の中心とする点対称移動です。
線対称移動は,ある直線を基準にして図形をひっくり返す移動です。 基準となる直線を「対称軸」といいます。
点対称移動は,ある点を中心として図形を\(180^{\circ}\)回転する移動です。 中心となる点を「回転の中心」といいます。
まずは,それぞれの対称移動で点がどこに移るのか確認してみましょう。 下図は点\((3, 1)\)をそれぞれの方法で対称移動したものです。
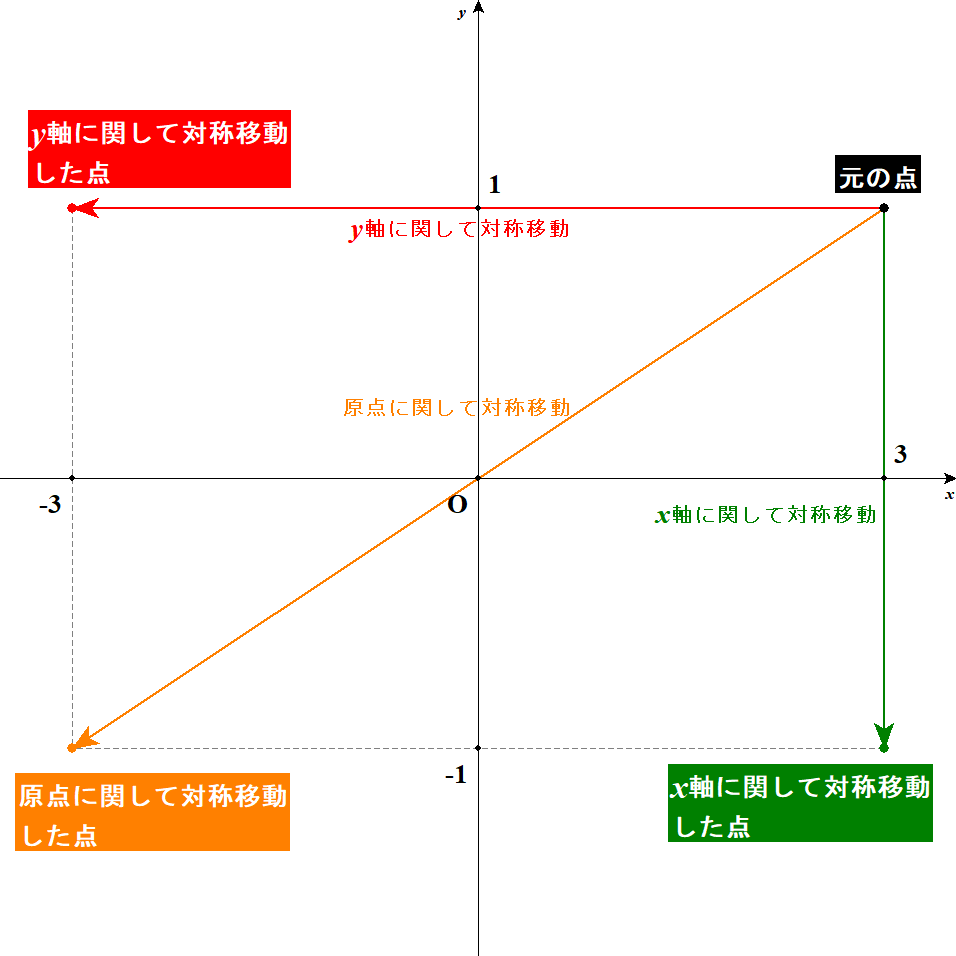
この図からも,点\((p, q)\)は対称移動によって,次の点に移ることが分かります。
| 対称移動 | 移動後の座標 |
|---|---|
| 元の点 | \((p, q)\) |
| \(x\)軸に関して対称移動 | \((p, \textcolor{red}{-q})\) |
| \(y\)軸に関して対称移動 | \((\textcolor{red}{-p}, q)\) |
| 原点に関して対称移動 | \((\textcolor{red}{-p}, \textcolor{red}{-q})\) |
\(x\)軸に関して対称移動したときは,\(x\)座標はそのままです。 \(y\)軸に関して対称移動したときは,\(y\)座標はそのままです。 それ以外の座標は符号が反転していますね。
次に,グラフを対称移動するとどうなるのか確認してみましょう。 先ほど点の対称移動を確認しました。 グラフは点の集まりですから,グラフの対称移動も点の対称移動と同様に符号が変化します。
つまり,グラフ上の点\((x, y)\)は,対称移動したあと次の点に移ります。
| 対称移動 | 移動後の座標 |
|---|---|
| 元の点 | \((x, y)\) |
| \(x\)軸に関して対称移動 | \((x, \textcolor{red}{-y})\) |
| \(y\)軸に関して対称移動 | \((\textcolor{red}{-x}, y)\) |
| 原点に関して対称移動 | \((\textcolor{red}{-x}, \textcolor{red}{-y})\) |
これを踏まえると,対称移動したあとのグラフの方程式は,\(x, y\)の符号を適切に変えてやれば求められることが分かります。 関数\(y = f(x)\)のグラフを対称移動したあとのグラフの方程式は,次のようになります。
| 対称移動 | 移動後のグラフ |
|---|---|
| 元のグラフ | \(y = f(x)\) |
| \(x\)軸に関して対称移動 | \(\textcolor{red}{-y} = f(x)\) |
| \(y\)軸に関して対称移動 | \(y = f(\textcolor{red}{-x})\) |
| 原点に関して対称移動 | \(\textcolor{red}{-y} = f(\textcolor{red}{-x})\) |
下図はグラフの対称移動の例で,\(y = (x - 3)^2 + 1\)のグラフをそれぞれの方法で対称移動したものです。
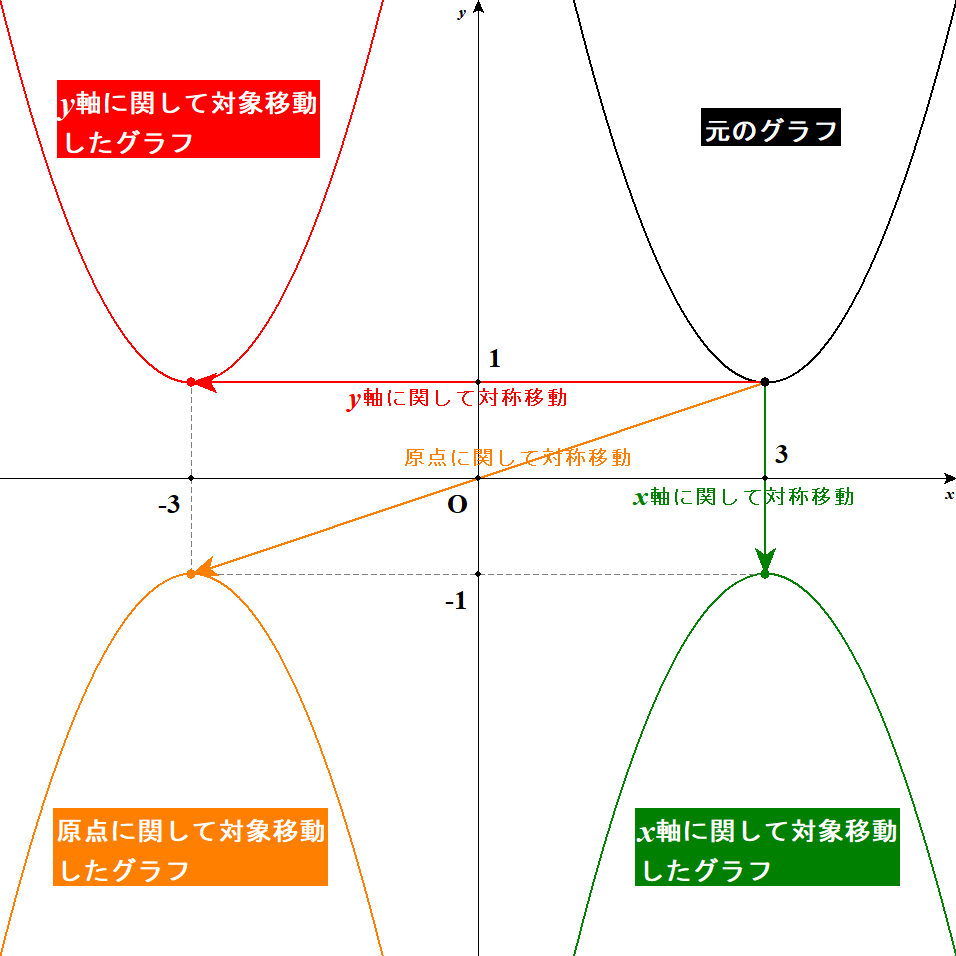
ひとつだけ,対称移動後のグラフの方程式を求める練習をしておきましょう。 上の放物線\(y = (x - 3)^2 + 1\)を\(y\)軸に関して対称移動すると,次の方程式が得られます。
放物線の頂点の座標が,ちゃんと\((3, 1)\)から\((-3, 1)\)に移ったことも確認できますね。
他にもグラフの移動には,回転移動などもありますが,今の時点で扱える内容ではありません。 複素数平面や行列の知識が必要となりますが,これは数学Ⅲや数学Cで学ぶ内容です。 (教育課程によって,数学Ⅲで複素数平面を学んだり,数学Cで行列を学んだりします。)
確認問題
関数\(y = x^2 + \displaystyle\frac{1}{x}\)のグラフを次の(1)~(3)の方法で平行移動します。 平行移動後のグラフの方程式をそれぞれ求めてください。
-
\(x\)軸方向に\(2\)だけ平行移動
-
\(y\)軸方向に\(-1\)だけ平行移動
-
\(x\)軸方向に\(-1\),\(y\)軸方向に\(3\)だけ平行移動
答え
平行移動後の方程式がどうなるか分かっていれば簡単です。
-
\(x\)を\(x - 2\)に変えれば良いです。
\( \begin{align} y &= (x - 2)^2 + \displaystyle\frac{1}{x - 2} \\[5pt] &= x^2 - 4x + 4 + \displaystyle\frac{1}{x - 2} \end{align} \)より,答えは\(y = x^2 - 4x + 4 + \displaystyle\frac{1}{x - 2}\)です。
-
\(y\)を\(y + 1\)に変えれば良いです。
\( \begin{align} y + 1 &= x^2 + \displaystyle\frac{1}{x} \\[5pt] \end{align} \)より,答えは\(y = x^2 - 1 + \displaystyle\frac{1}{x}\)です。
-
\(x\)を\(x + 1\)に,\(y\)を\(y - 3\)に変えれば良いです。
\( \begin{align} y - 3 &= (x + 1)^2 + \displaystyle\frac{1}{x + 1} \\[5pt] &= x^2 + 2x + 1 + \displaystyle\frac{1}{x + 1} \end{align} \)より,答えは\(y = x^2 + 2x + 4 + \displaystyle\frac{1}{x + 1}\)です。
関数\(y = x^3 + \displaystyle\frac{2}{x^2 + 2}\)のグラフを次の(1)~(4)の方法で対称移動します。 対称移動後のグラフの方程式をそれぞれ求めてください。
-
\(x\)軸に関して対称移動
-
\(y\)軸に関して対称移動
-
原点に関して対称移動
-
\(x\)軸に関して対称移動後,原点に関して対称移動
答え
対称移動後の方程式がどうなるか分かっていれば簡単です。
-
\(y\)を\(-y\)に変えれば良いです。
\( \begin{align} -y = x^3 + \displaystyle\frac{2}{x^2 + 2} \end{align} \)より,答えは\(y = -x^3 - \displaystyle\frac{2}{x^2 + 2}\)です。
-
\(x\)を\(-x\)に変えれば良いです。
\( \begin{align} y &= (-x)^3 + \displaystyle\frac{2}{(-x)^2 + 2} \\[5pt] &= -x^3 + \displaystyle\frac{2}{x^2 + 2} \end{align} \)より,答えは\(y = -x^3 + \displaystyle\frac{2}{x^2 + 2}\)です。
-
\(x\)を\(-x\)に,\(y\)を\(-y\)に変えれば良いです。
\( \begin{align} -y &= (-x)^3 + \displaystyle\frac{2}{(-x)^2 + 2} \\[5pt] &= -x^3 + \displaystyle\frac{2}{x^2 + 2} \end{align} \)より,答えは\(y = x^3 - \displaystyle\frac{2}{x^2 + 2}\)です。
-
まず\(y\)を\(-y\)に変えます。
\( \begin{align} -y = x^3 + \displaystyle\frac{2}{x^2 + 2} \end{align} \)次に\(x\)を\(-x\)に,\(y\)を\(-y\)に変えれば良いです。
\( \begin{align} -(-y) &= (-x)^3 + \displaystyle\frac{2}{(-x)^2 + 2} \\[5pt] &= -x^3 + \displaystyle\frac{2}{x^2 + 2} \end{align} \)より,答えは\(y = -x^3 + \displaystyle\frac{2}{x^2 + 2}\)です。
次の問いに答えてください。
-
関数\(y = x^2 + 2x\)のグラフを\(y\)軸に関して対称移動したあと,\(x\)軸方向に\(-3\)だけ平行移動し,原点に関して対称移動したグラフの方程式を求めてください。
-
ある関数のグラフを\(y\)軸に関して対称移動したあと,\(x\)軸方向に\(-3\)だけ平行移動し,原点に関して対称移動したグラフの方程式が\(y = x^2 + 2x\)であったとき,元の関数を求めてください。
答え
平行移動や対称移動をひとつずつ順番に行っていきましょう。
-
まず\(x\)を\(-x\)に変えます。
\( \begin{align} y &= (-x)^2 + 2 \cdot (-x) \\[5pt] &= x^2 - 2x \end{align} \)次に\(x\)を\(x + 3\)に変えます。
\( \begin{align} y &= (x + 3)^2 - 2(x + 3) \\[5pt] &= x^2 + 6x + 9 -2x - 6 \\[5pt] &= x^2 +4x + 3 \end{align} \)最後に\(x\)を\(-x\)に,\(y\)を\(-y\)に変えれば良いです。
\( \begin{align} -y &= (-x)^2 + 4 \cdot (-x) + 3 \\[5pt] &= x^2 - 4x + 3 \end{align} \)より,答えは\(y = -x^2 + 4x - 3\)です。
-
移動後のグラフが分かっているので,逆向きの移動を行って,元のグラフにたどり着きましょう。 まず原点に関して対称移動し,次に\(x\)軸方向に\(3\)だけ平行移動し,\(y\)軸に関して対称移動すれば良いですね。
まず\(x\)を\(-x\)に,\(y\)を\(-y\)に変えます。
\( \begin{align} -y &= (-x)^2 + 2 \cdot (-x) \\[5pt] &= x^2 - 2x \end{align} \)次に\(x\)を\(x - 3\)に変えます。
\( \begin{align} -y &= (x - 3)^2 - 2(x - 3) \\[5pt] &= x^2 - 6x + 9 - 2x + 6 \\[5pt] &= x^2 - 8x + 15 \end{align} \)最後に\(x\)を\(-x\)に変えれば良いです。
\( \begin{align} -y &= (-x)^2 - 8 \cdot (-x) + 15 \\[5pt] &= x^2 + 8x + 15 \end{align} \)より,答えは\(y = -x^2 - 8x - 15\)です。
