2次関数のグラフをかけるようになりましたが,それで満足してはいけません。 グラフからどんなことが分かるか,分析することが重要です。 今回は「いつ最大・最小になるか」という基本的な情報を見抜けるようにしましょう。
目次
定義域が実数全体の場合
まずは定義域が実数全体の場合の最大値・最小値を調べてみましょう。 グラフを一目見れば分かるので,さっそく関数\(y = (x - 2)^2 + 4\)のグラフを見てみます。
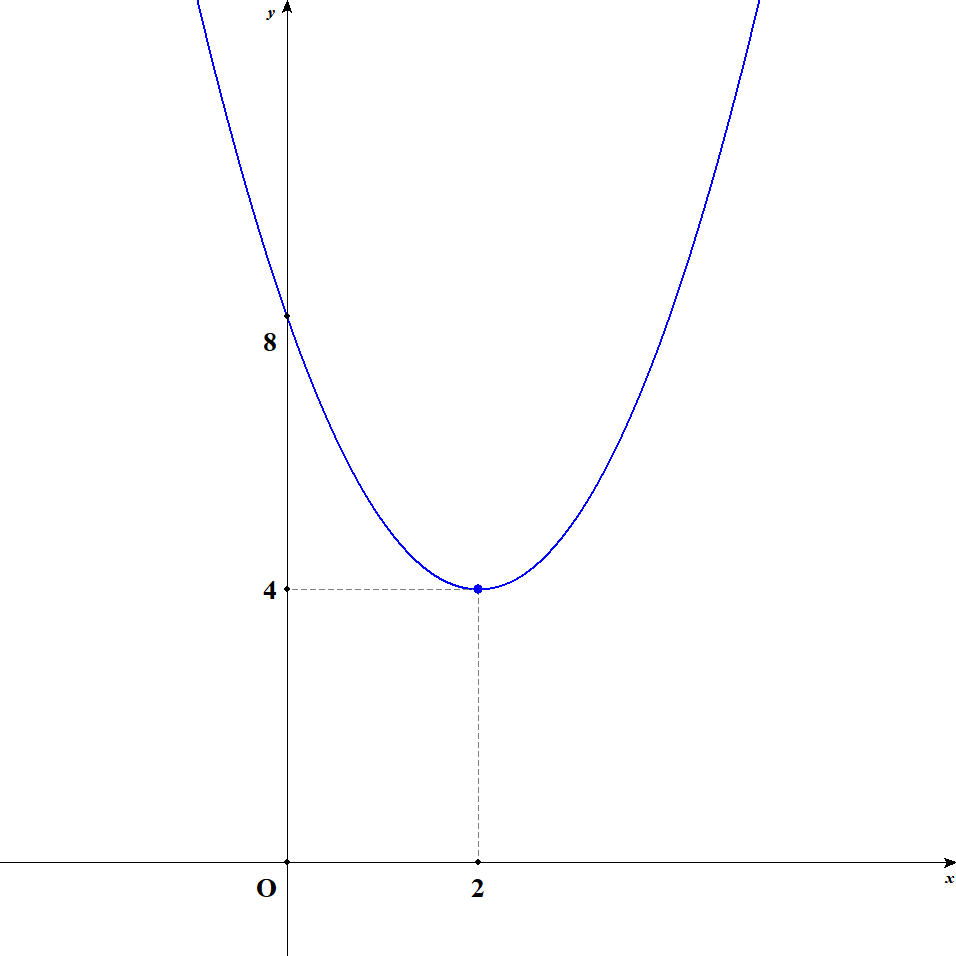
グラフを見ると,この関数は\(x = 2\)のとき最小値\(4\)をとることが分かりますね。 また,この関数の値はいくらでも大きくなるため,最大値が存在しないことも分かります。
これで勘付いた人も多いと思いますが,下に凸の放物線はみんな,頂点で最小値をとり,最大値はありません。 もちろん上に凸であれば,頂点で最大値をとり,最小値はありません。 どちらにせよ,グラフさえかければ一目で分かってしまいますね。
定義域が区間の場合
次に定義域が特定の区間である場合を考えてみます。 この場合もグラフさえかけてしまえば簡単ですが,定義域の端を含むかどうかに注意してください。
さらっと区間という言葉を使っていますが,とりあえず「どこからどこまでという範囲が決まっているもの」と解釈してください。
例えば「\(1 \leqq x \leqq 2\)」,「\(2 < x < 5\)」,「\(3 \leqq x\)」は区間で,それぞれ\([1, 3]\),\((2, 5)\),\([3, \infty)\)とも表します。 端の値を含むとき\([\ ]\),含まないときに\((\ )\)という記号を使っています。 座標と同じ記号を使うのでややこしいですが,高校数学では使わないので覚える必要はありません。
ではさっそく例として,関数\(y = (x - 1)^2 + 1\)の最大値・最小値をいろいろな定義域で考えてみましょう。 まずは定義域を\(-1 \leqq x \leqq 2\)としてみます。 下図を見てください。
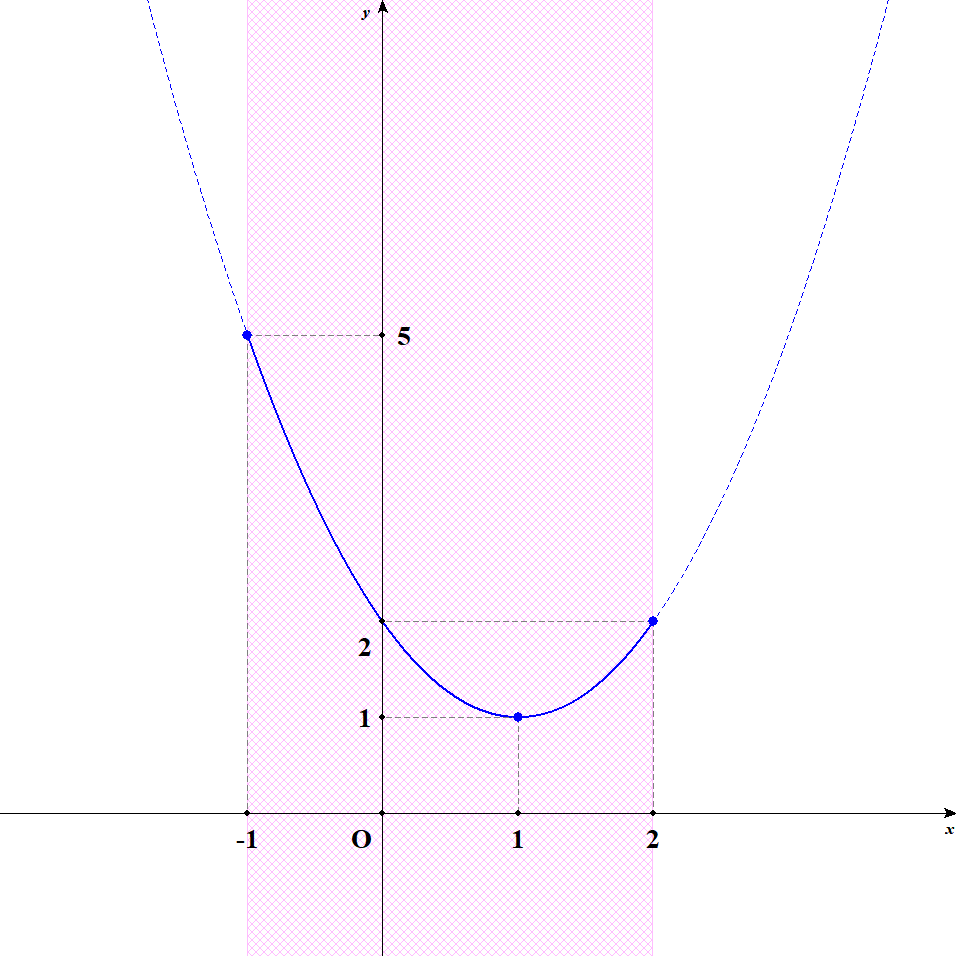
グラフさえかければ,最大値・最小値は一目瞭然ですね。 \(x = -1\)のとき最大値\(5\),\(x = 1\)のとき最小値\(1\)をとっています。 図のように定義域の範囲を分かりやすくかいておくと考えやすいです。
次に定義域を\(2 \leqq x < 3\)として考えてみます。 下図を見てください。
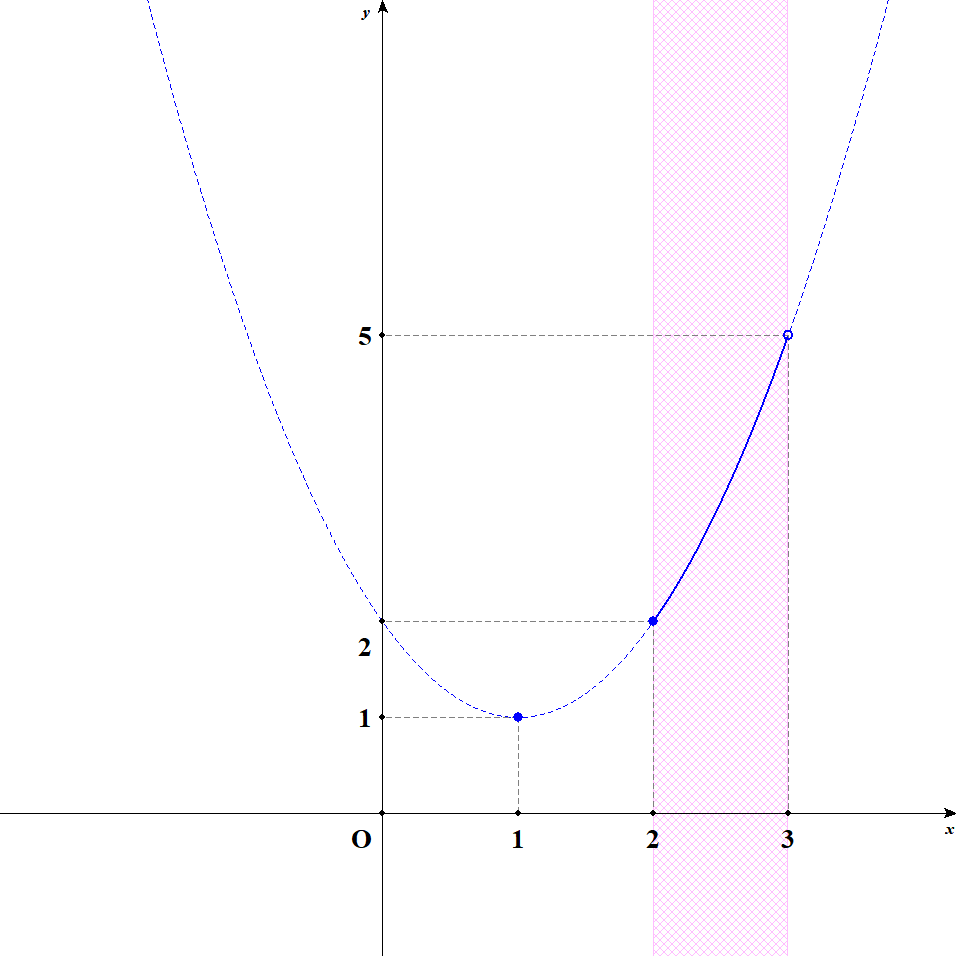
これもグラフを見れば最大値・最小値が分かりますが,定義域の端には注意してください。 一見\(x = 3\)のとき最大値\(5\)をとりそうですが,\(x = 3\)は定義域に含まれていません。 この関数に最大値はないのです。 最小値については,\(x = 2\)のときに\(2\)をとりますね。
最大値・最小値を考えるときのポイントについて,これまでの例で何か気づきましたか? 下に凸の放物線を中心にポイントをまとめておきましょう。
ひとつは,頂点が定義域に含まれる限り,頂点の値が最小値になることです。 下に凸の放物線では,頂点は一番低いところにあるから当然ですね。 もちろん上に凸なら,頂点で最大となります。
もうひとつは,軸から離れれば離れるほど,関数の値が大きくなっていくことです。 最大値を考えるときは,軸からどれだけ離れているかを参考にできるわけですね。 もちろん上に凸なら,軸から離れるほど,関数の値は小さくなります。
確認問題
次の関数の最大値・最小値を求めてください。 ただし,定義域は実数全体とします。
-
\(y = x^2 + 6x - 2\)
-
\(y = -2x^2 + 4x\)
-
\(y = x^2 + x + 1\)
答え
グラフをかけば分かるのですが,定義域が実数全体なので,わざわざグラフをかくまでもありません。 グラフが上に凸か下に凸か,頂点がどこにあるかを確認して,放物線の形を思い浮かべれば最大値・最小値が分かるでしょう。
-
\(x^2\)の係数が正なので,グラフの放物線は下に凸です。 また,関数式を平方完成すると,次のようになります。
\( \begin{align} y &= x^2 + 6x - 2 \\[5pt] &= (x + 3)^2 - 9 - 2 \\[5pt] &= (x + 3)^2 - 11 \end{align} \)したがって,放物線の頂点の座標は\((-3, -11)\)です。 定義域が実数全体であり,放物線が下に凸であることから,\(x = -3\)で最小値\(-11\)をとり,最大値はないことが分かります。
-
\(x^2\)の係数が負なので,グラフの放物線は上に凸です。 また,関数式を平方完成すると,次のようになります。
\( \begin{align} y &= -2x^2 + 4x \\[5pt] &= -2(x^2 - 2x) \\[5pt] &= -2\{(x - 1)^2 - 1\} \\[5pt] &= -2(x - 1)^2 + 2 \end{align} \)したがって,放物線の頂点の座標は\((1, 2)\)です。 定義域が実数全体であり,放物線が上に凸であることから,\(x = 1\)で最大値\(2\)をとり,最小値はないことが分かります。
-
\(x^2\)の係数が正なので,グラフの放物線は下に凸です。 また,関数式を平方完成すると,次のようになります。
\( \begin{align} y &= x^2 + x + 1 \\[5pt] &= \left(x + \displaystyle\frac{1}{2}\right)^2 - \displaystyle\frac{1}{4} + 1 \\[5pt] &= \left(x + \displaystyle\frac{1}{2}\right)^2 + \displaystyle\frac{3}{4} \end{align} \)したがって,放物線の頂点の座標は\(\left(-\displaystyle\frac{1}{2}, \displaystyle\frac{3}{4}\right)\)です。 定義域が実数全体であり,放物線が下に凸であることから,\(x = -\displaystyle\frac{1}{2}\)で最小値\(\displaystyle\frac{3}{4}\)をとり,最大値はないことが分かります。
関数\(y = x^2 - 4x + 7\)について,次の定義域での最大値・最小値を求めてください。
-
\(0 \leqq x \leqq 3\)
-
\(0 < x \leqq 3\)
-
\(2 \leqq x \leqq 4\)
-
\(2 < x < 4\)
-
\(1 \leqq x \leqq 3\)
-
\(1 < x \leqq 3\)
答え
まずグラフの頂点を求めておきます。 関数式を平方完成すると,次のようになります。
これで放物線の頂点が\((2, 3)\)であることが分かりました。 あとはグラフをかいて考えましょう。
-
グラフは次のようになります。
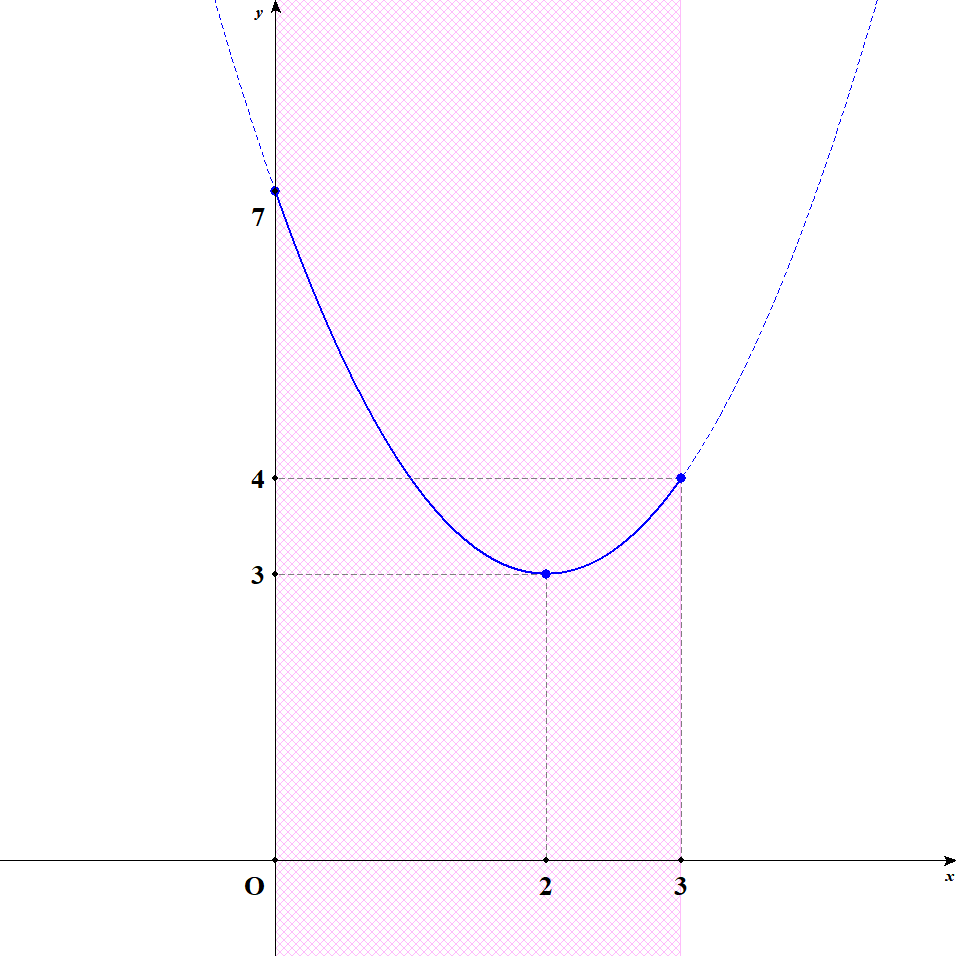
グラフから,\(x = 0\)のとき最大値\(7\)をとり,\(x = 2\)のとき最小値\(3\)をとることが分かります。
ちなみに,こんなに真面目にグラフをかかなくても最大値・最小値は求められます。 まず軸が定義域に含まれている時点で,最小値は軸での値です。 また,定義域の端の値のうち,軸からより離れている方が最大値をとります。 下に凸の放物線は軸から離れるほど値が大きくなるからですね。
-
グラフは次のようになります。
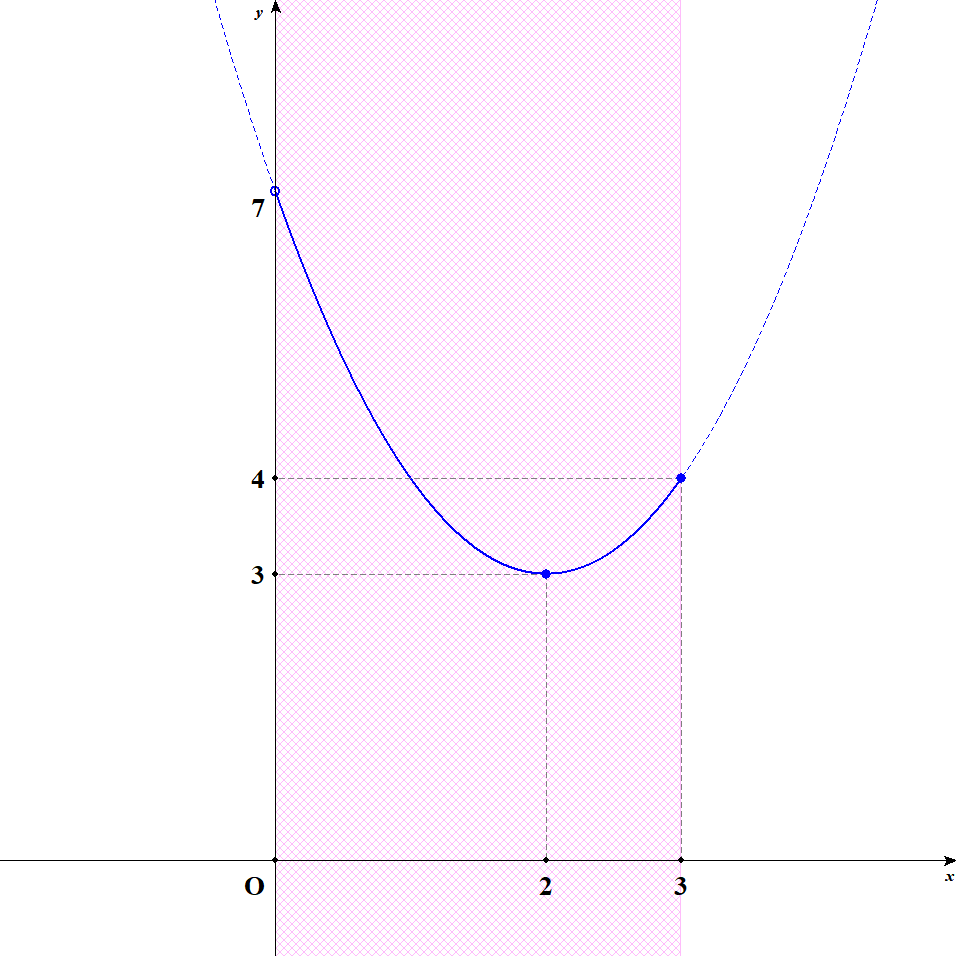
グラフから,\(x = 2\)のとき最小値\(3\)をとり,最大値はないことが分かります。 \(x = 0\)で最大値をとりそうですが,そこは定義域に含まれていません。
-
グラフは次のようになります。
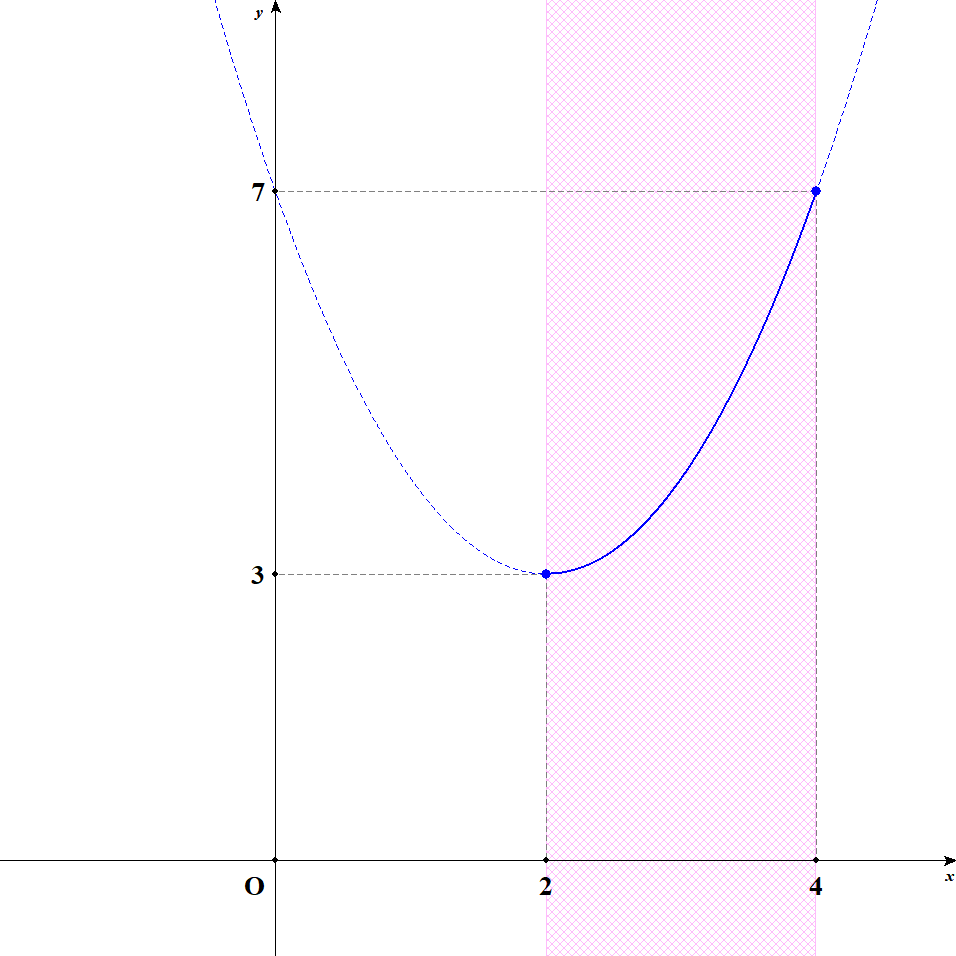
グラフから,\(x = 4\)のとき最大値\(7\)をとり,\(x = 2\)のとき最小値\(3\)をとることが分かります。
-
グラフは次のようになります。
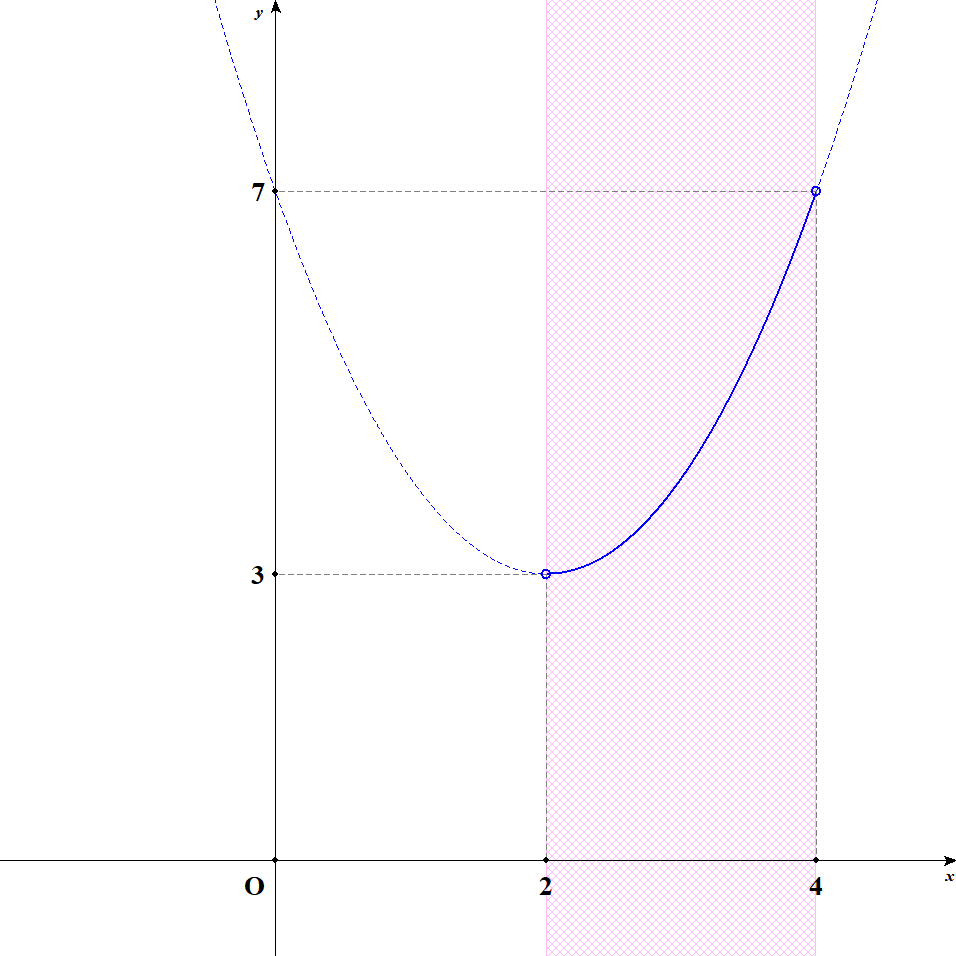
グラフから,最大値も最小値もないことが分かります。
-
グラフは次のようになります。
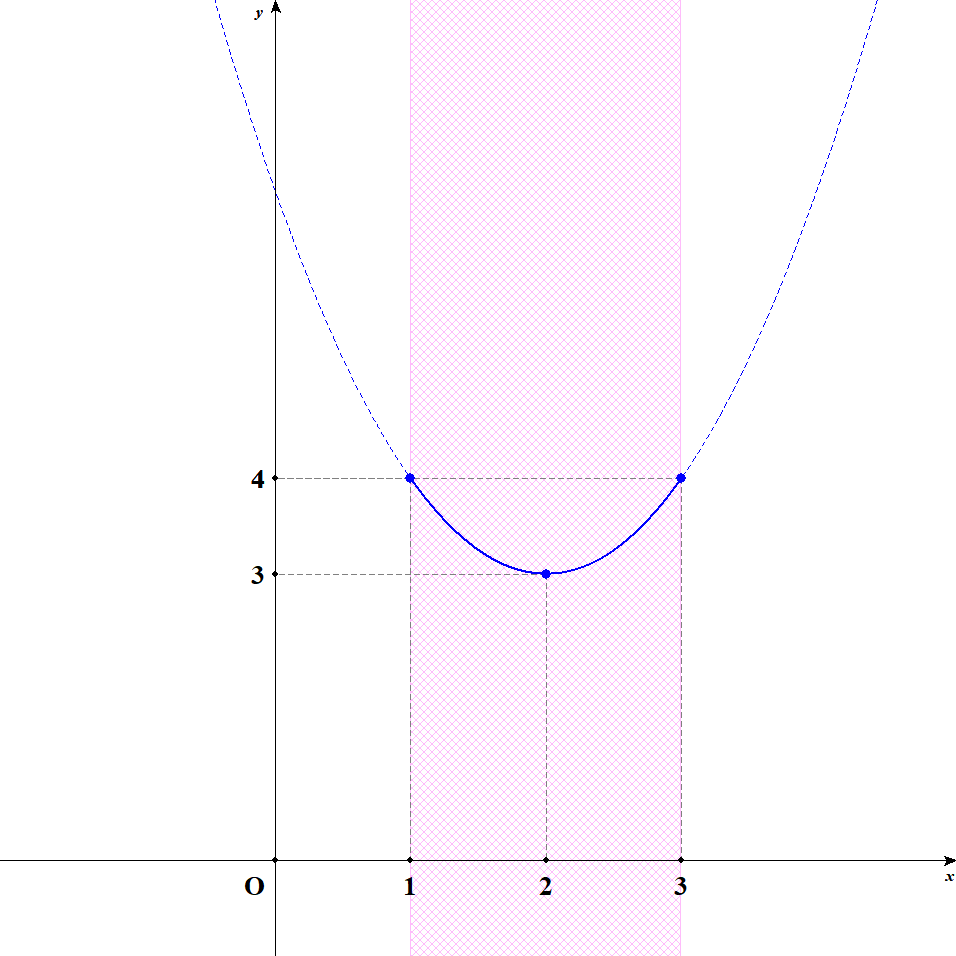
グラフから,\(x = 1, 3\)のとき最大値\(4\)をとり,\(x = 2\)のとき最小値\(3\)をとることが分かります。
-
グラフは次のようになります。
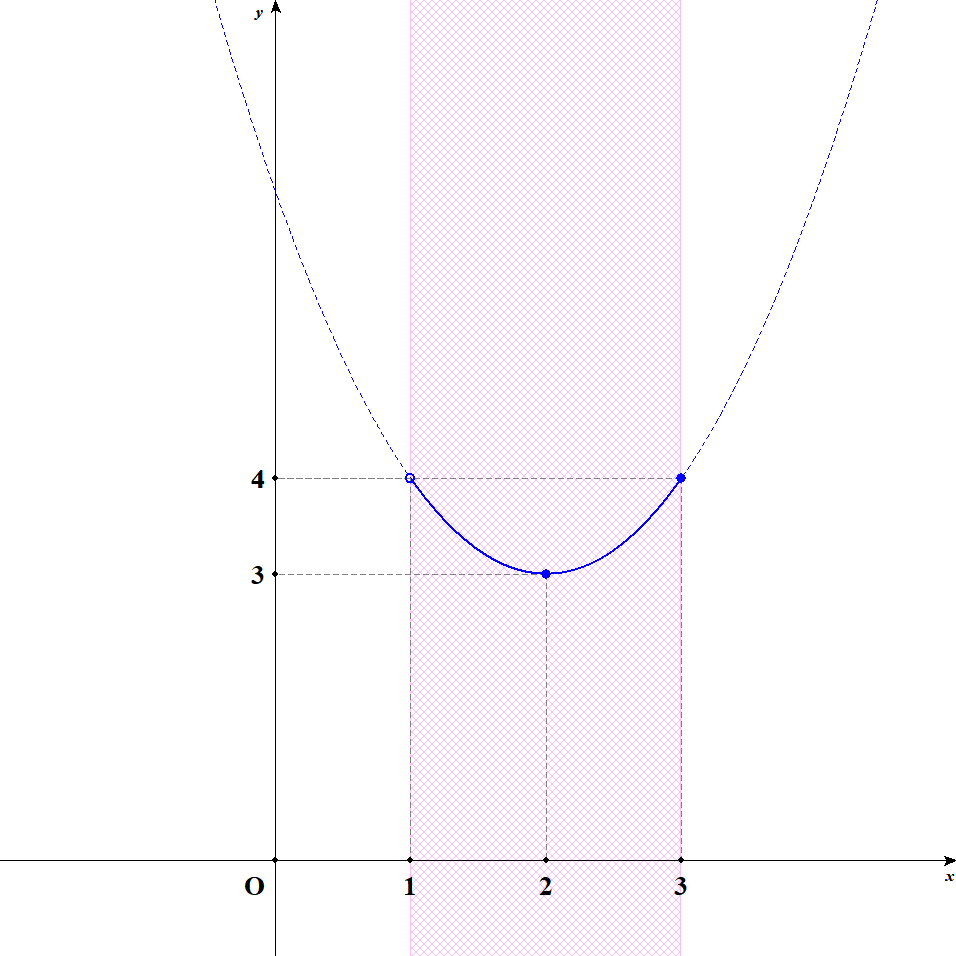
グラフから,\(x = 3\)のとき最大値\(4\)をとり,\(x = 2\)のとき最小値\(3\)をとることが分かります。
ある2次関数のグラフが上に凸の放物線であることが分かっています。 この関数は定義域上に最大値を持ちますが,最小値はありません。 また,最大値は頂点での値であることが分かっています。
この関数の式と定義域の組み合わせについて,あり得るものを次の(1)~(4)からすべて選んで答えてください。
-
\(y = -x^2 + 2x + 2 \quad (2 \leqq x < 3)\)
-
\(y = -x^2 + 6x + 5 \quad (2 < x \leqq 5)\)
-
\(y = -x^2 - 4x - 2 \quad (-5 < x \leqq -2)\)
-
\(y = -x^2 - 2x + 1 \quad (-4 \leqq x < 4)\)
答え
それぞれグラフをかいてみて,問題の条件に当てはまるかを調べれば良いですが,かなり面倒です。 この問題では,最大値や最小値の具体的な値までは必要ないので,ちゃんとしたグラフをかかなくてもOKです。 軸と定義域の位置関係が分かるような簡単な図をかいて解いてみましょう。
-
平方完成すると
\( \begin{align} y &= -x^2 + 2x + 2 \\[5pt] &= -(x^2 - 2x) + 2 \\[5pt] &= -(x - 1)^2 + 3 \end{align} \)なので,軸は\(x = 1\)です。 定義域との位置関係をみると,下図のようになります。
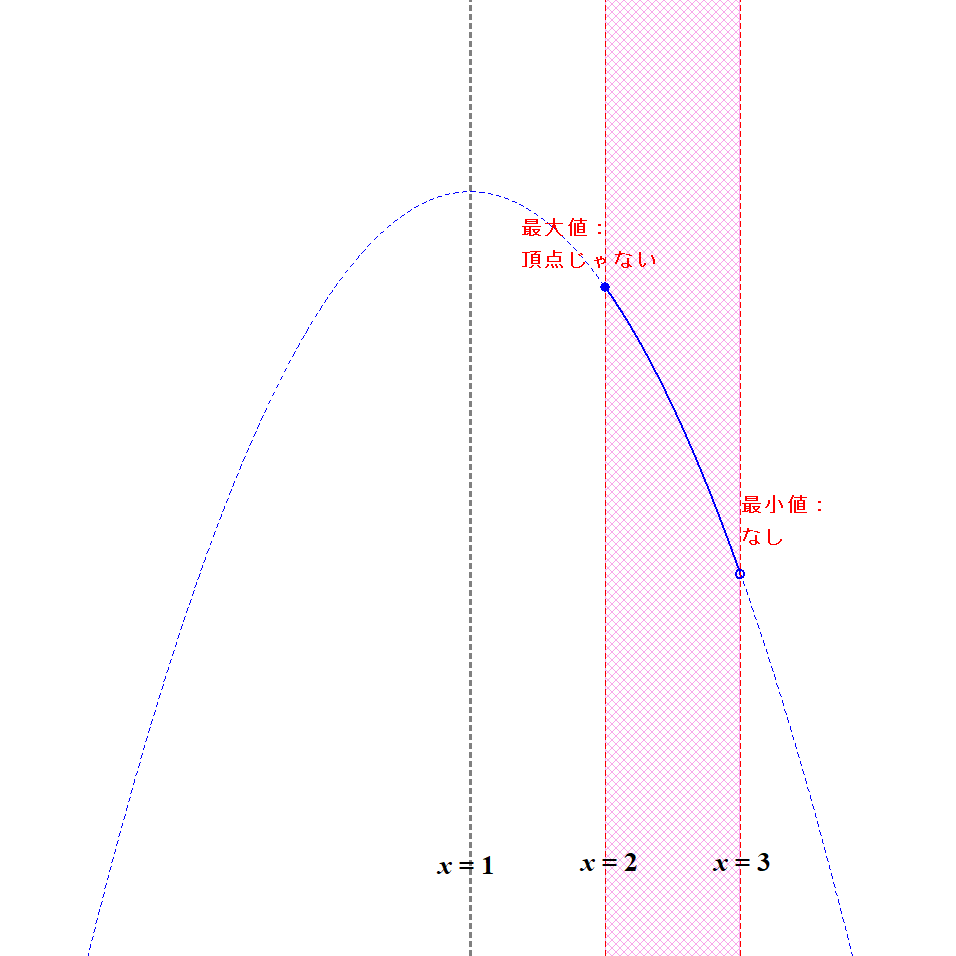
これは条件とは合いませんね。 軸が定義域に含まれておらず,最大値になりません。
-
平方完成すると
\( \begin{align} y &= -x^2 + 6x + 5 \\[5pt] &= -(x^2 - 6x) + 5 \\[5pt] &= -(x - 3)^2 + 14 \end{align} \)なので,軸は\(x = 3\)です。 定義域との位置関係をみると,下図のようになります。
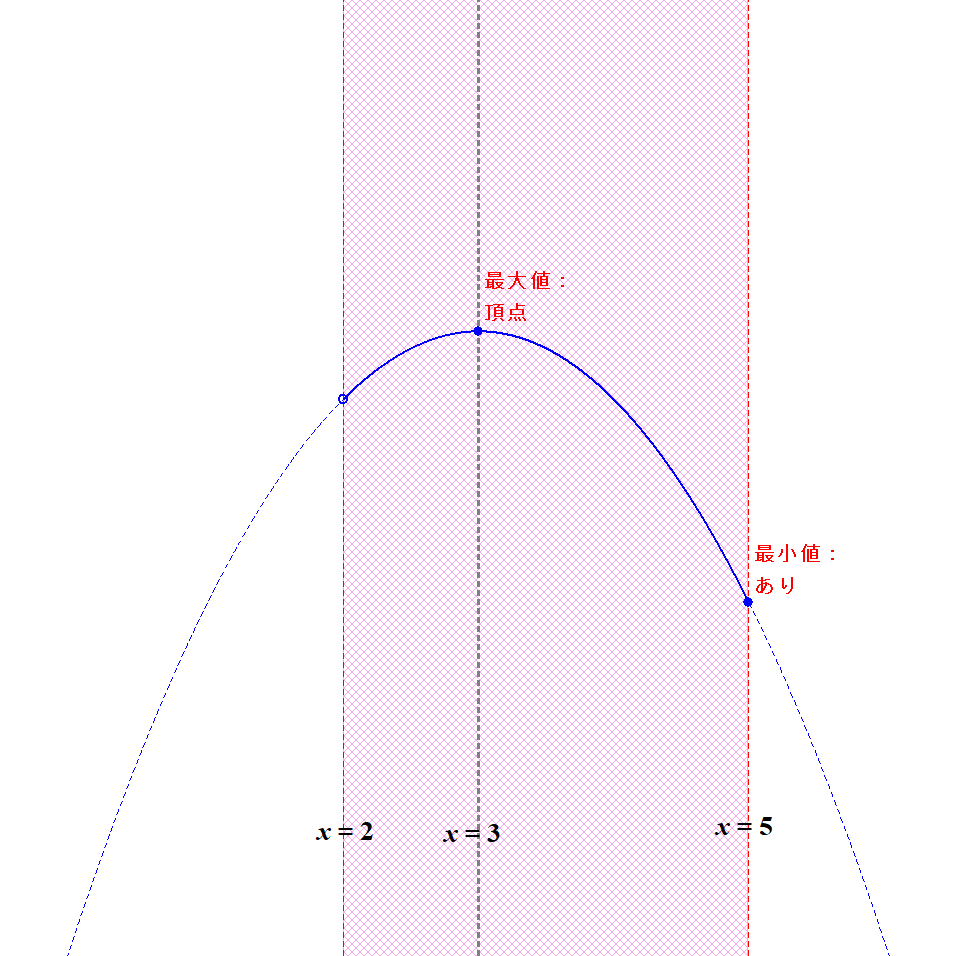
これは条件とは合いませんね。 定義域の端のうち,軸から遠い\(x = 5\)の地点で最小値をとります。
-
平方完成すると
\( \begin{align} y &= -x^2 - 4x - 2 \\[5pt] &= -(x^2 + 4x) - 2 \\[5pt] &= -(x + 2)^2 + 2 \end{align} \)なので,軸は\(x = -2\)です。 定義域との位置関係をみると,下図のようになります。
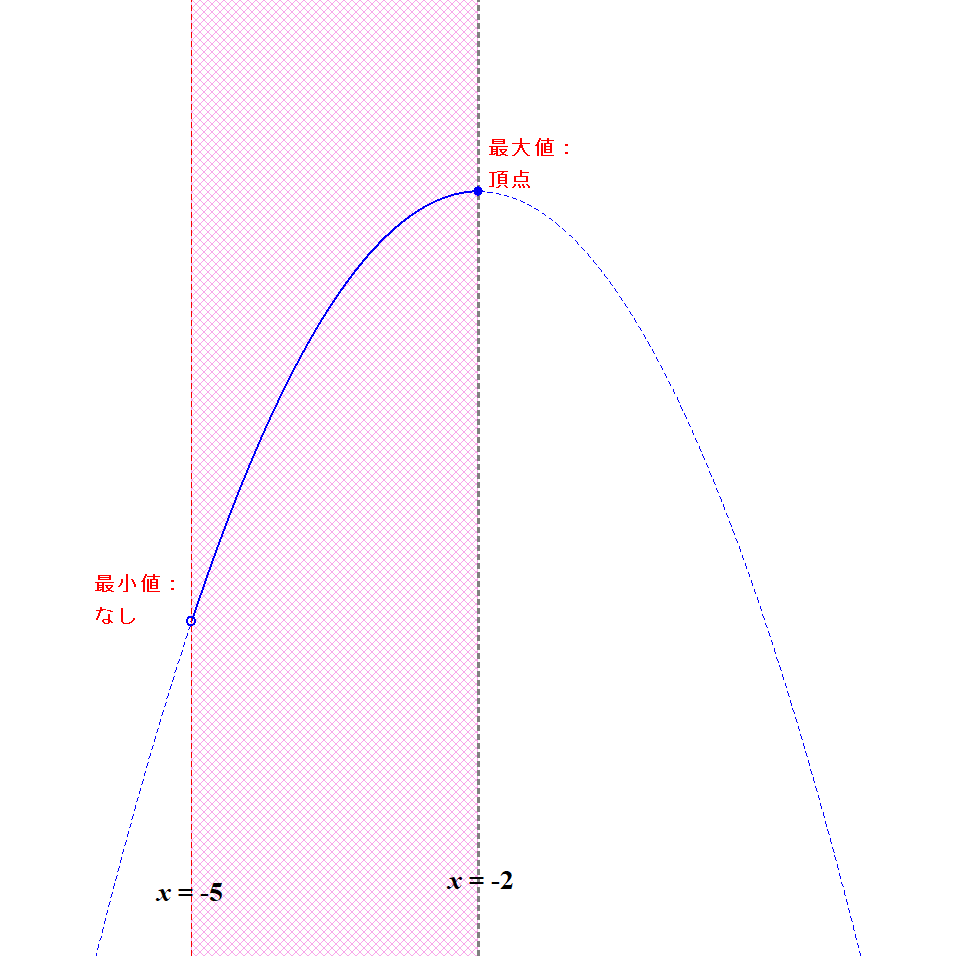
これは条件に合っていますね。
-
平方完成すると
\( \begin{align} y &= -x^2 - 2x + 1 \\[5pt] &= -(x^2 + 2x) + 1 \\[5pt] &= -(x + 1)^2 + 2 \end{align} \)なので,軸は\(x = -1\)です。 定義域との位置関係をみると,下図のようになります。
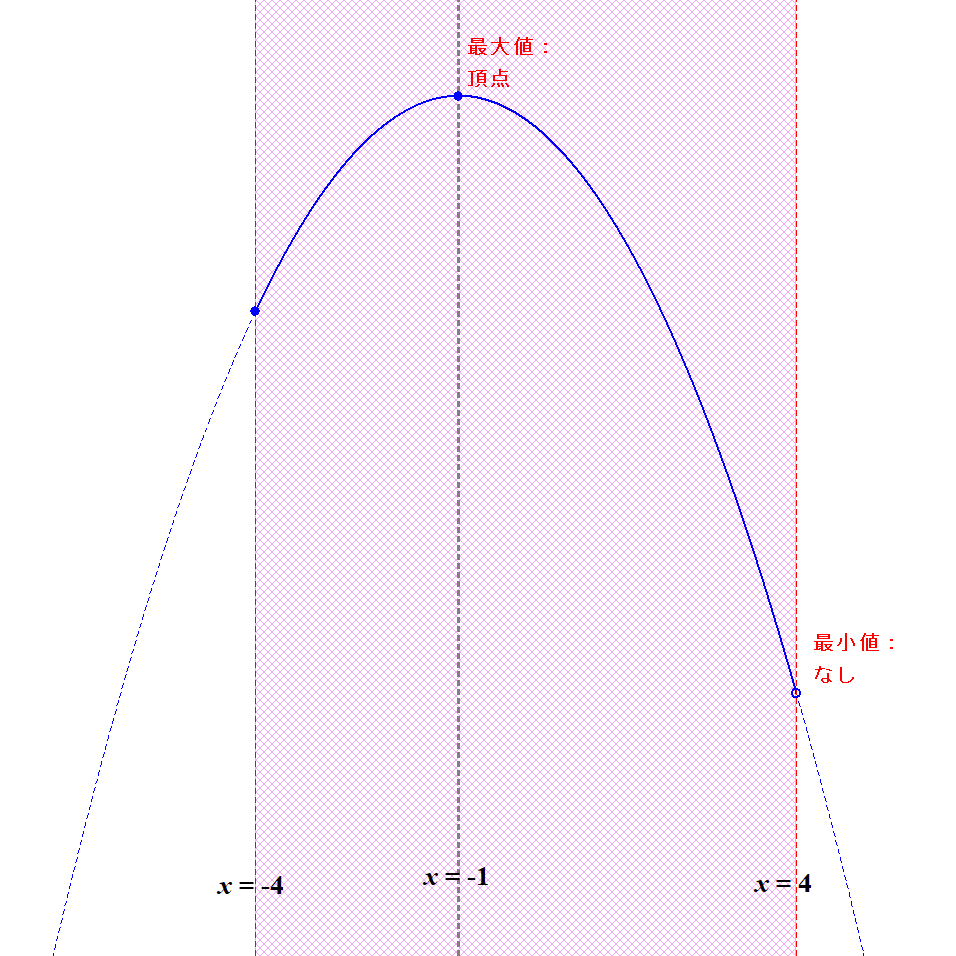
これは条件に合っていますね。
以上より,答えは(3),(4)です。
