文字定数を含む２次関数

はじめに

今回は文字定数を含む２次関数を考えます。そうすることで「最も～な２次関数は？」とか「この２次関数が最も～になるのはどんなとき？」といったことが柔軟に考えられるようになります。

縦に動く２次関数

▼

補足いきなりの補足ですが

タイトルに「動く」と入れましたが，これは定数の値を変えると，グラフの位置が変わるという意味で使っています。

定義域を\(-2 \leqq x \leqq 1\)とする関数\(y = x^2 + 2x + a\)の最大値・最小値を考えてみましょう。ただし\(a\)は定数です。関数を平方完成すると，次のようになります。

\( \begin{align} y &= x^2 + 2x + a \\[5pt] &= (x + 1)^2 + a - 1 \end{align} \)

この関数のグラフは点\((-1, a - 1)\)を頂点とする放物線ですから，そのグラフは次のようになります。

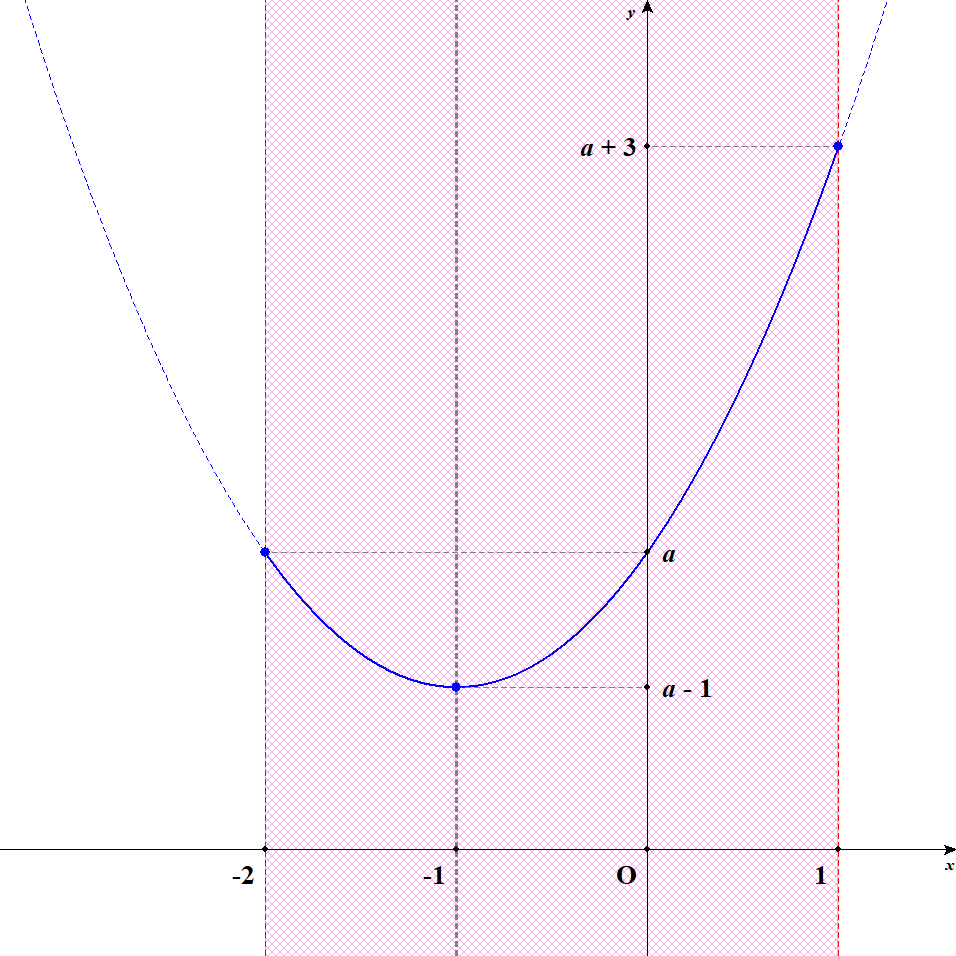
\(a\)の値を変えるとグラフはどうなるでしょうか？軸は常に\(x = -1\)なので，グラフの横方向の位置は変わりません。しかし，頂点の\(y\)座標は\(a - 1\)ですから，グラフの縦方向の位置はいろいろ変わります。

つまり\(a\)の値を変えると，グラフは縦に動くのです。グラフを縦に動かすのをイメージして，最大値・最小値がどうなるか考えてみましょう。最小値はいつも頂点だし，最大値はいつも\(x = 1\)での値だと分かりますね。

というわけで，この関数は\(x = 1\)のとき最大値\(a + 3\)をとり，\(x = -1\)のとき最小値\(a - 1\)をとります。

どこで最大値・最小値をとるかは，軸と定義域の端がどれくらい離れているかによります。グラフが横に動かない限りは，軸と定義域の位置関係は変わりませんから，どこで最大値・最小値をとるかは簡単に分かります。

横にも動く２次関数

▲

▼

縦にしか動かない２次関数は簡単でした。軸と定義域の位置関係が変わらないので，どこで最大値・最小値をとるかが簡単に分かったのです。しかし，グラフが横にも動くとなると話は別です。

定義域を\(-1 \leqq x \leqq 1\)とする関数\(y = x^2 - 4ax + a\)の最大値・最小値を考えてみましょう。 \(a\)は定数です。関数を平方完成すると，次のようになります。

\( \begin{align} y &= x^2 - 4ax + a \\[5pt] &= (x - 2a)^2 - 4a^2 + a \end{align} \)

この関数のグラフは点\((2a, -4a^2 + a)\)を頂点とする放物線ですから，そのグラフは例えば次のようになります。

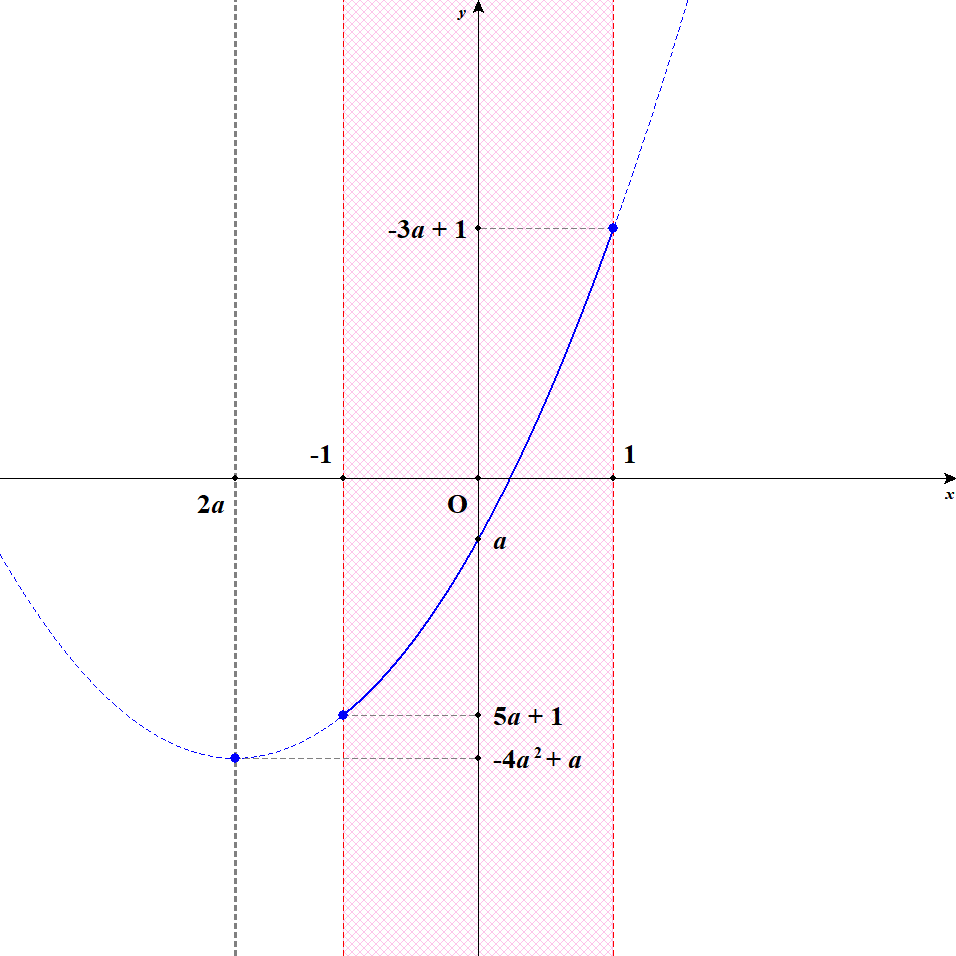
この場合，軸\(x = 2a\)が定義域の左の外側にあります。このとき，\(x = 1\)のとき最大値\(-3a + 1\)をとり，\(x = -1\)のとき最小値\(5a + 1\)をとりますね。

では，この関数の最大値・最小値はこれで答えとして良いでしょうか？答えはＮＯです。例えば，軸が定義域の中に入る場合は，最小値は頂点での値\(-4a^2 + a\)に変わるはずです。

というわけで，どうやらこの問題の答えを出すには，\(a\)の値で場合分けする必要があるようです。これから考えていきましょう。

軸が左の果てから右に移動してくるのをイメージしましょう。軸が定義域より左側にあるうちは，上のグラフのように\(x = 1\)のとき最大値，\(x = -1\)のとき最小値をとります。軸が定義域の中に入ると，最小値が頂点に変わります。

ということは，軸が定義域の左側にある間，つまり\(2a < -1\)であるうちは，\(x = 1\)のとき最大値\(-3a + 1\)，\(x = -1\)のとき最小値\(5a + 1\)をとるわけです。

では，軸を定義域の中に入れていきましょう。軸が定義域に入ると，次のグラフのようになります。

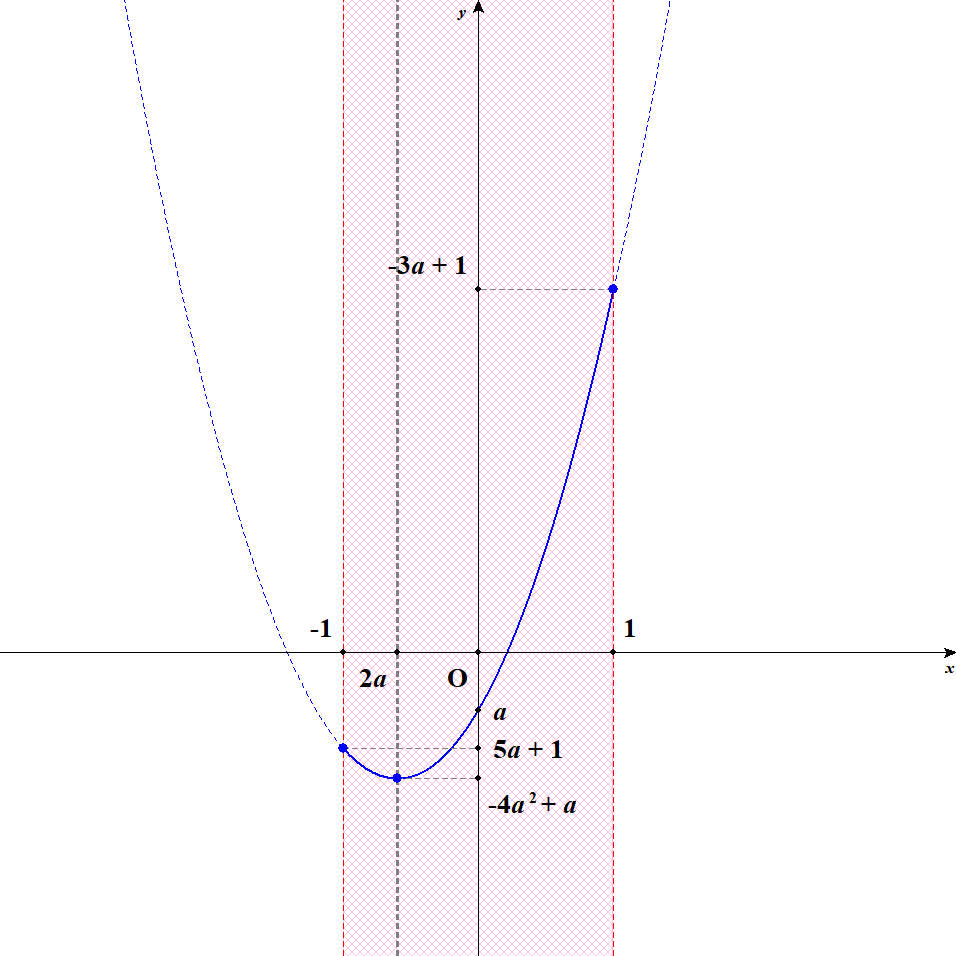
最小値は頂点ですね。最大値は定義域の端のうち，軸からより離れたところでとりますから，\(x = 1\)で最大値をとります。軸が定義域のちょうど真ん中までくると，\(x = -1\)でも最大値をとるようになります。

ということは，軸が定義域内の左寄りにある間，つまり\(-1 \leqq 2a < 0\)であるうちは，\(x = 1\)のとき最大値\(-3a + 1\)，\(x = 2a\)のとき最小値\(-4a^2 + a\)をとるわけです。

次に考えるのは，軸がちょうど定義域の真ん中に来たときですね。このとき，グラフは次のようになります。

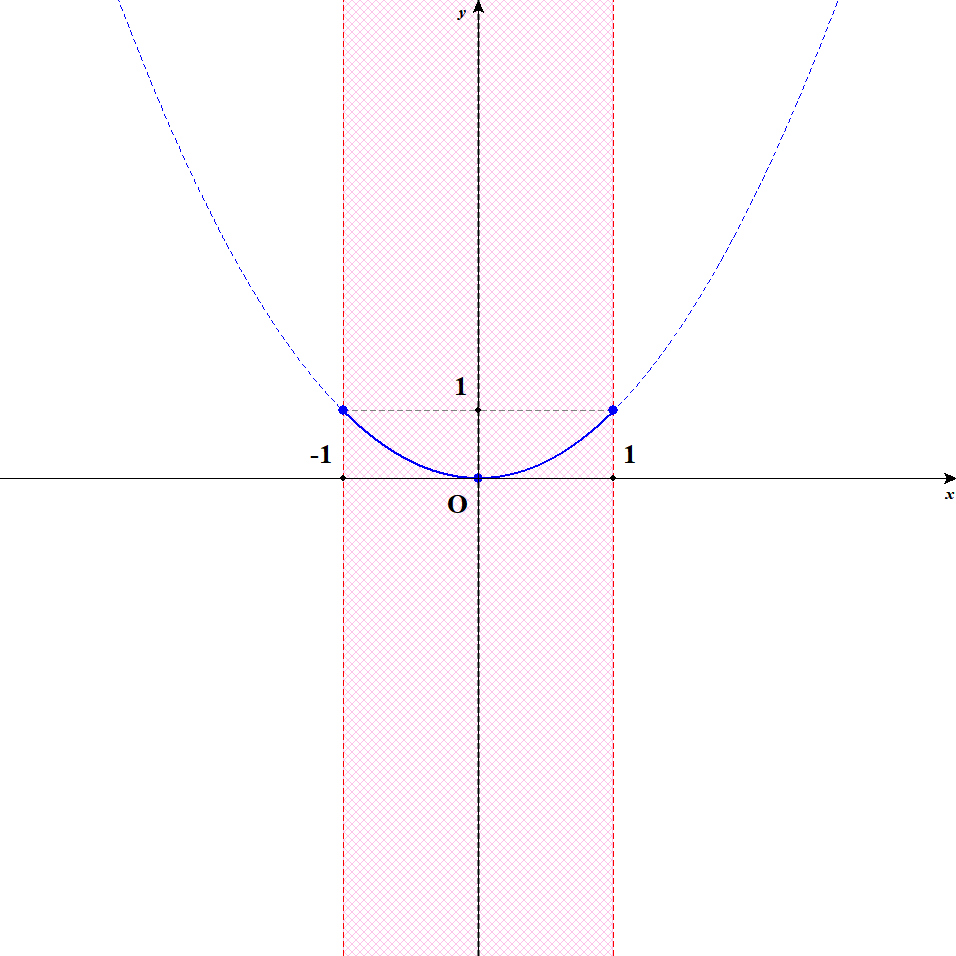
最小値は頂点です。軸は定義域のちょうど真ん中にありますから，軸から定義域の端までの距離は，右端でも左端でも変わりません。なので，最大値は定義域の右端と左端の両方でとります。

軸が定義域のちょうど真ん中にある間，つまり\(2a = 0\)であるうちは，\(x = -1, 1\)のとき最大値\(1\)，\(x = 0\)のとき最小値\(0\)をとるわけですね。

補足 \(a\)が登場しない？

軸が定義域の真ん中に来るのは\(2a = 0\)，つまり\(a = 0\)のときです。このとき，\(a\)の値がはっきり決まっているので，最大値・最小値の値も具体的に求められます。

最大値は\(x = -1, 1\)でとりますが，\(x = -1\)のときの関数の値は\(5a + 1\)で，\(x = 1\)のときの関数の値は\(-3a + 1\)ですね。これらに\(a = 0\)を代入すると，どちらも\(1\)になることが分かります。

最小値は\(x = 2a\)でとりますが，このときの関数の値は\(-4a^2 + a\)ですね。これに\(a = 0\)を代入すると，\(0\)になることが分かります。

次は軸が定義域の真ん中を越えて，定義域の中の右寄りに来ます。グラフは次のようになりますね。

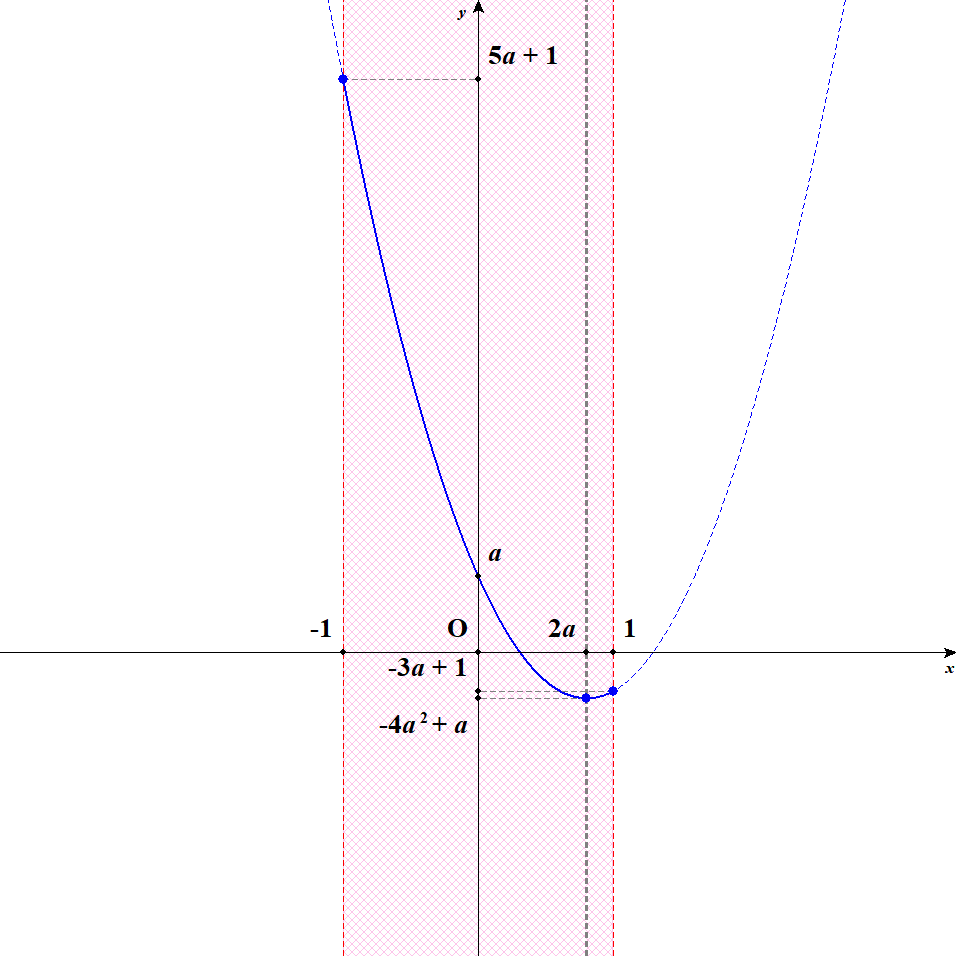
このとき，軸はまだ定義域の中にあるので，最小値は頂点です。最大値は定義域の端のうち，軸からより離れたところでとりますから，\(x= -1\)で最大値をとります。このまま軸が定義域の中にあるうちは，このように最大値・最小値をとります。

ということは，軸が定義域内の右寄りにある間，つまり\(0 < 2a \leqq 1\)であるうちは，\(x = -1\)のとき最大値\(5a + 1\)，\(x = 2a\)のとき最小値\(-4a^2 + a\)をとります。

最後に，軸が定義域を通り抜けて，右側の外に出た後のことを考えましょう。グラフは次のようになります。

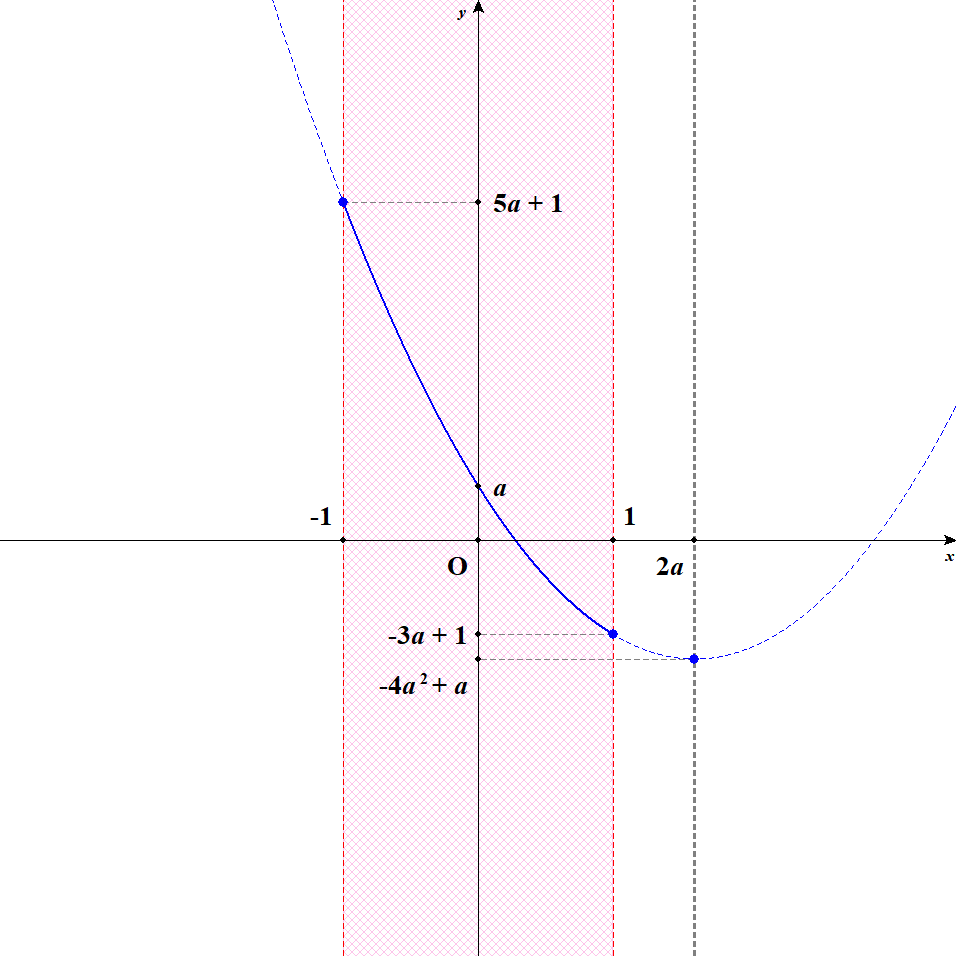
このとき，グラフから\(x = -1\)のとき最大値をとり，\(x = 1\)のとき最小値をとることが分かります。

軸が定義域の右側にある間，つまり\(2a > 1\)であるうちは，\(x = -1\)のとき最大値\(5a + 1\)，\(x = 1\)のとき最小値\(-3a + 1\)をとるわけですね。

以上をまとめると，この関数の最大値・最小値は次のようになります。

\(a\)の範囲	最大値	最小値
\(a < -\displaystyle\frac{1}{2}\)	\(x = 1\)のとき \(-3a + 1\)	\(x = -1\)のとき \(5a + 1\)
\(-\displaystyle\frac{1}{2} \leqq a < 0\)	\(x = 1\)のとき \(-3a + 1\)	\(x = 2a\)のとき \(-4a^2 + a\)
\(a = 0\)	\(x = -1, 1\)のとき \(1\)	\(x = 0\)のとき \(0\)
\(0 < a \leqq \displaystyle\frac{1}{2}\)	\(x = -1\)のとき \(5a + 1\)	\(x = 2a\)のとき \(-4a^2 + a\)
\(a > \displaystyle\frac{1}{2}\)	\(x = -1\)のとき \(5a + 1\)	\(x = 1\)のとき \(-3a + 1\)

場合分けが多くて難しいと思うかもしれませんが，グラフの軸が左から右へ動いていくのをイメージすると考えやすいです。

その際，「軸が定義域の中にあるか外にあるか」と「軸が定義域の中にある場合，それが左寄り・真ん中・右寄りのどこにあるか」の２点を意識しましょう。

拡がる定義域

▲

▼

ここまで定数を含む関数を考えてきました。次は定数を含む定義域を考えてみましょう。

\(1 \leqq x \leqq a\)を定義域とする関数\(y = x^2 - 6x + 12\)の最大値・最小値を考えます。 \(a\)は\(a > 1\)を満たす定数です。関数を平方完成すると，次のようになります。

\( \begin{align} y &= x^2 - 6x + 12 \\[5pt] &= (x - 3)^2 + 3 \end{align} \)

このグラフの軸は\(x = 3\)ですね。定義域がだんだん右に拡がっていくのをイメージして，いくつかグラフをかいてみましょう。

まずは定義域の右端が軸よりも左にある場合です。グラフは次のようになります。

このときは，軸から遠い\(x = 1\)のとき最大値\(7\)を，軸に近い\(x = a\)のとき最小値\(a^2 - 6a + 12\)をとります。定義域が軸に届くまでの間，つまり\(1 < a < 3\)であるうちは，このように最大値・最小値をとります。

次に定義域が軸に届いてからのことを考えます。グラフは次のようになります。

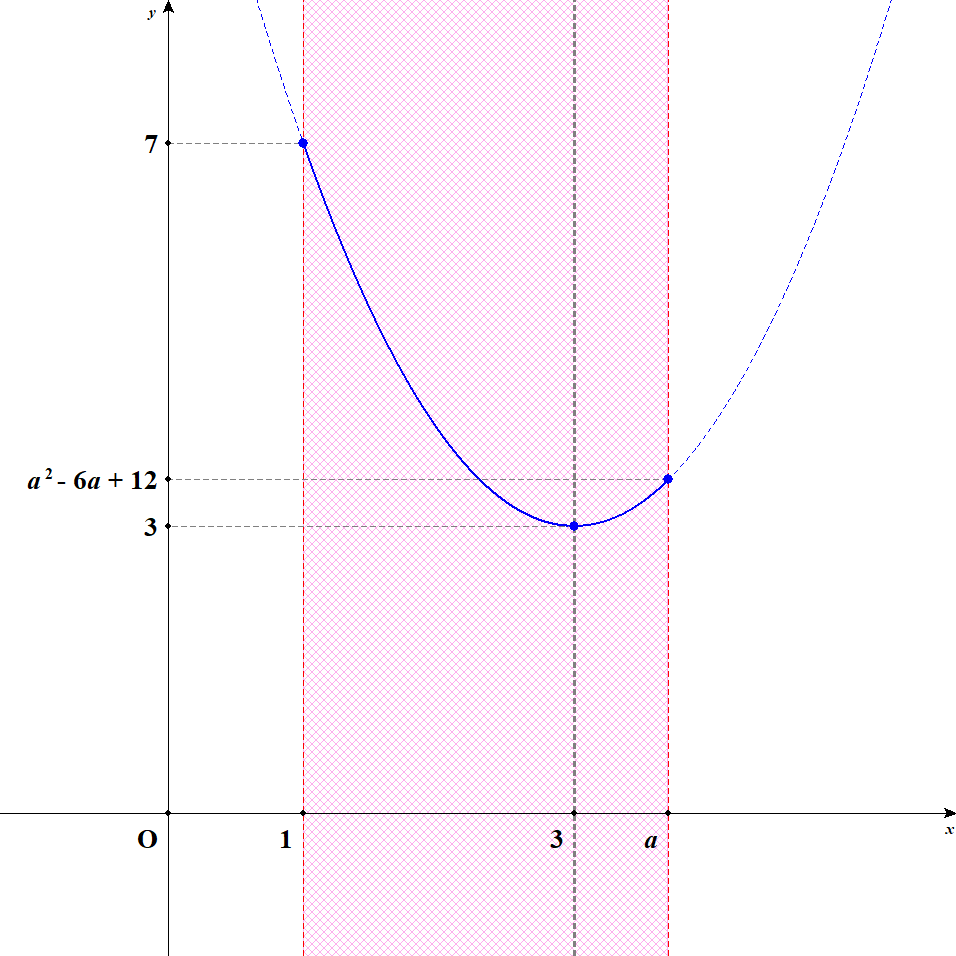
軸が定義域の中に入ったので，最小値は頂点でとりますね。最大値は定義域の端のうち，軸から遠い方でとります。軸と定義域の左端との距離は\(2\)ですから，軸と定義域の右端との距離が\(2\)未満であるうちは，左端で最大値をとります。

つまり，\(3 \leqq a < 5\)であるうちは，\(x = 1\)で最大値\(7\)をとり，\(x = 3\)で最小値\(3\)をとります。

次は軸が定義域のちょうど真ん中になった場合です。グラフは次のようになります。

このとき，定義域の右端でも最大値をとります。軸から定義域の右端までの距離が，左端までの距離\(2\)と同じなので，\(a = 3 + 2 = 5\)となります。

つまり，\(a = 5\)である間，\(x = 1, 5\)のとき最大値\(7\)をとり，\(x = 3\)のとき最小値\(3\)をとります。

最後に，定義域の右端がさらに右まで進んだときを考えます。グラフは次のようになります。

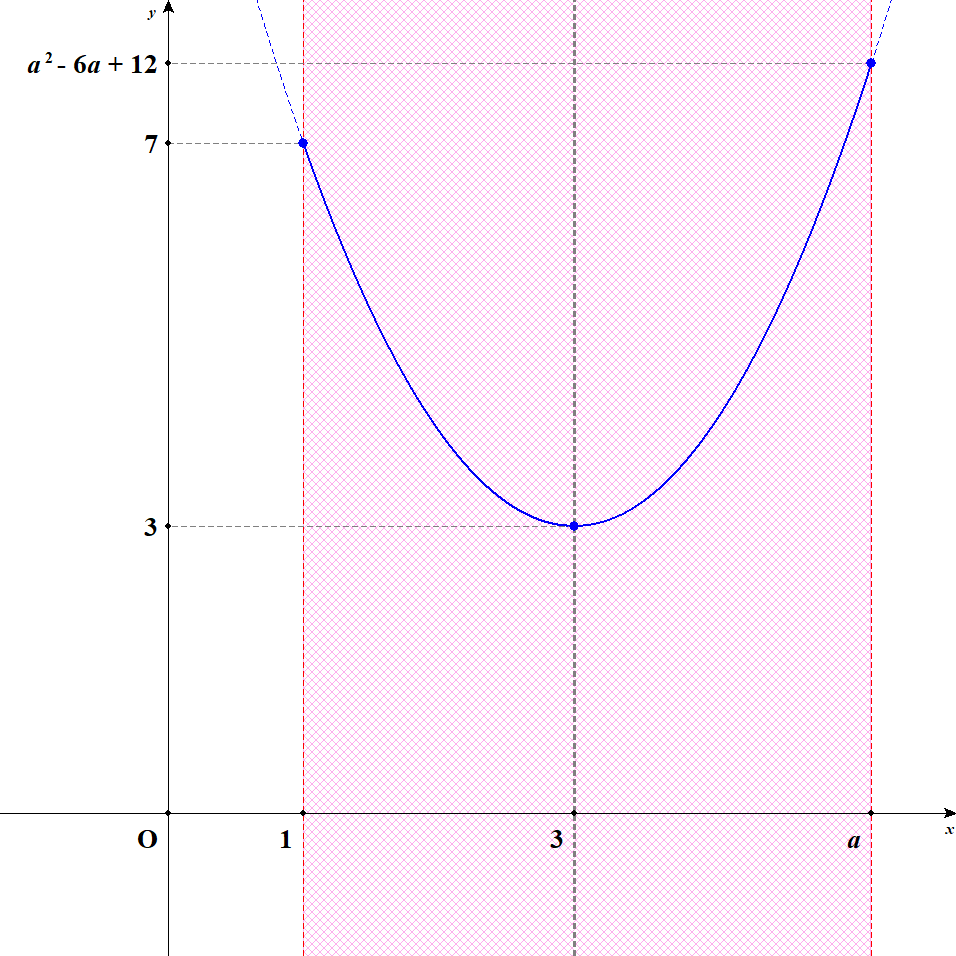
このとき，軸から定義域の右端までの距離は，左端までよりも遠くなっています。これで左端では最大値をとらなくなり，右端で最大値をとるようになります。

つまり，\(a > 5\)である間，\(x = a\)のとき最大値\(a^2 - 6a + 12\)をとり，\(x = 3\)のとき最小値\(3\)をとります。

以上をまとめると，この関数の最大値・最小値は次のようになります。

\(a\)の範囲	最大値	最小値
\(1 < a < 3\)	\(x = 1\)のとき \(7\)	\(x = a\)のとき \(a^2 - 6a + 12\)
\(3 \leqq a < 5\)	\(x = 1\)のとき \(7\)	\(x = 3\)のとき \(3\)
\(a = 5\)	\(x = 1, 5\)のとき \(7\)	\(x = 3\)のとき \(3\)
\(a > 5\)	\(x = a\)のとき \(a^2 - 6a + 12\)	\(x = 3\)のとき \(3\)

定数のあるところが関数でも定義域でも，考え方は変わりません。「軸が定義域の中にあるか外にあるか」と「軸が定義域の中にある場合，それが左寄り・真ん中・右寄りのどこにあるか」の２点を意識します。

動く定義域

▲

▼

定数を含む定義域をもうひとつ考えてみましょう。今度は定義域の両端に定数を含めます。

\(a \leqq x \leqq a + 2\)を定義域とする関数\(y = x^2 - 6x + 10\)の最大値・最小値を考えます。 \(a\)は定数です。関数を平方完成すると，次のようになります。

\( \begin{align} y &= x^2 - 6x + 10 \\[5pt] &= (x - 3)^2 + 1 \end{align} \)

このグラフの軸は\(x = 3\)ですね。では，これまで同様に，定義域が左の果てから右に動いてくるのをイメージしましょう。今回は定義域の幅が\(2\)で一定であることに注意です。

まずは定義域が軸に到達していない場合ですね。グラフは次のようになります。

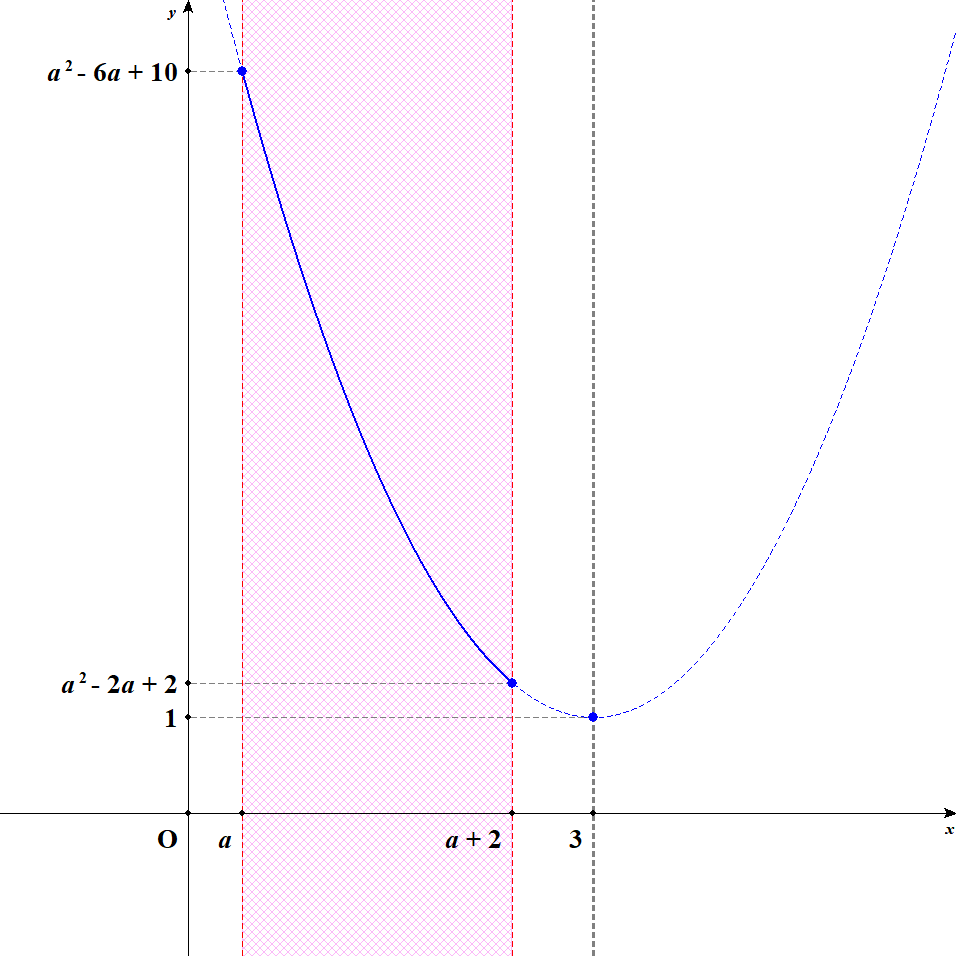
このとき，軸から遠い\(x = a\)のとき最大値\(a^2 - 6a + 10\)をとり，軸に近い\(x = a + 2\)のとき最小値\(a^2 - 2a + 2\)をとります。定義域が軸に到達しないのは，\(a + 2 < 3\)である間です。

つまり\(a < 1\)であるうちは，このように最大値・最小値をとります。

次は定義域が軸に到達した後を考えます。グラフは次のようになります。

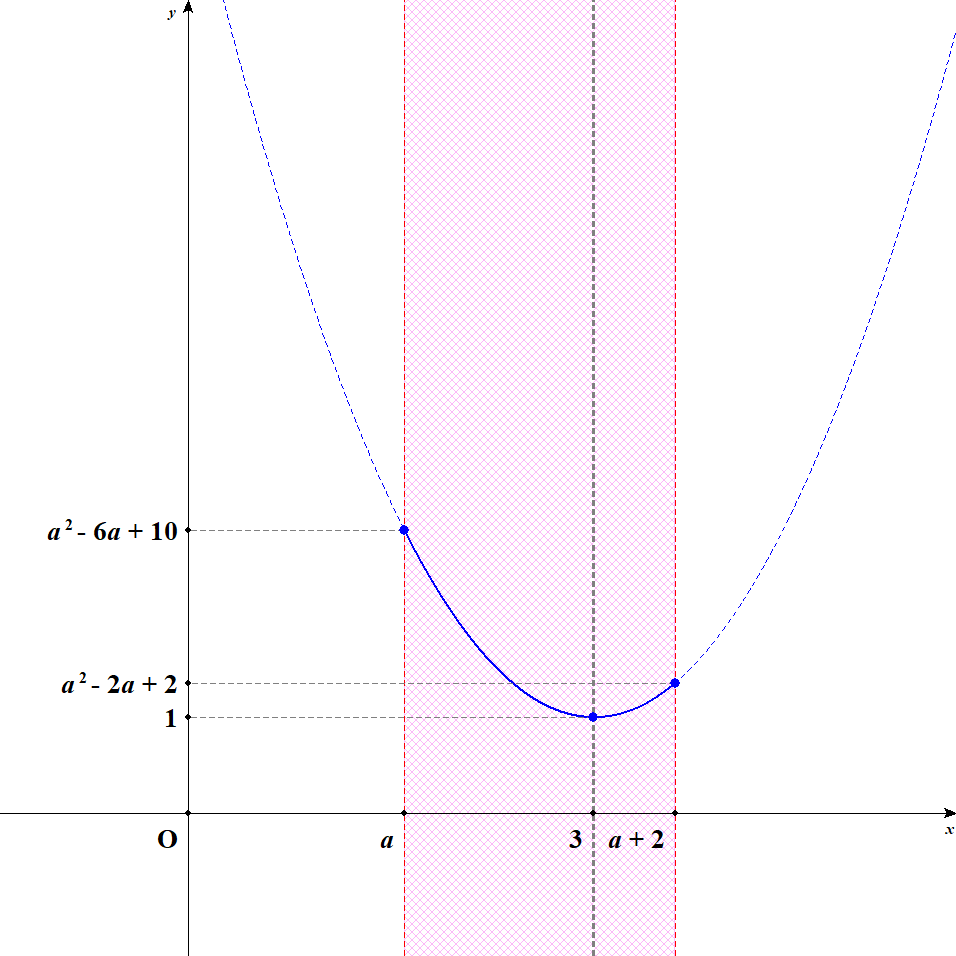
このとき，軸が定義域内にあるので，最小値は頂点でとります。最大値は定義域の端のうち，軸から遠い方でとるので，定義域が右に行き過ぎない限りは，左端の方で最大値をとります。

定義域の右端でも最大値をとるようになるのは，定義域のちょうど真ん中に軸があるときです。定義域の真ん中は\(\displaystyle\frac{a + (a + 2)}{2} = a + 1\)ですから，\(a + 1 = 3\)のときに初めて右端でも最大値をとります。

つまり，\(1 \leqq a < 2\)であるうちは，\(x = a\)のとき最大値\(a^2 - 6a + 10\)をとり，\(x = 3\)のとき最小値\(1\)をとります。

次は定義域の両端で最大値をとる場合です。グラフは次のようになります。

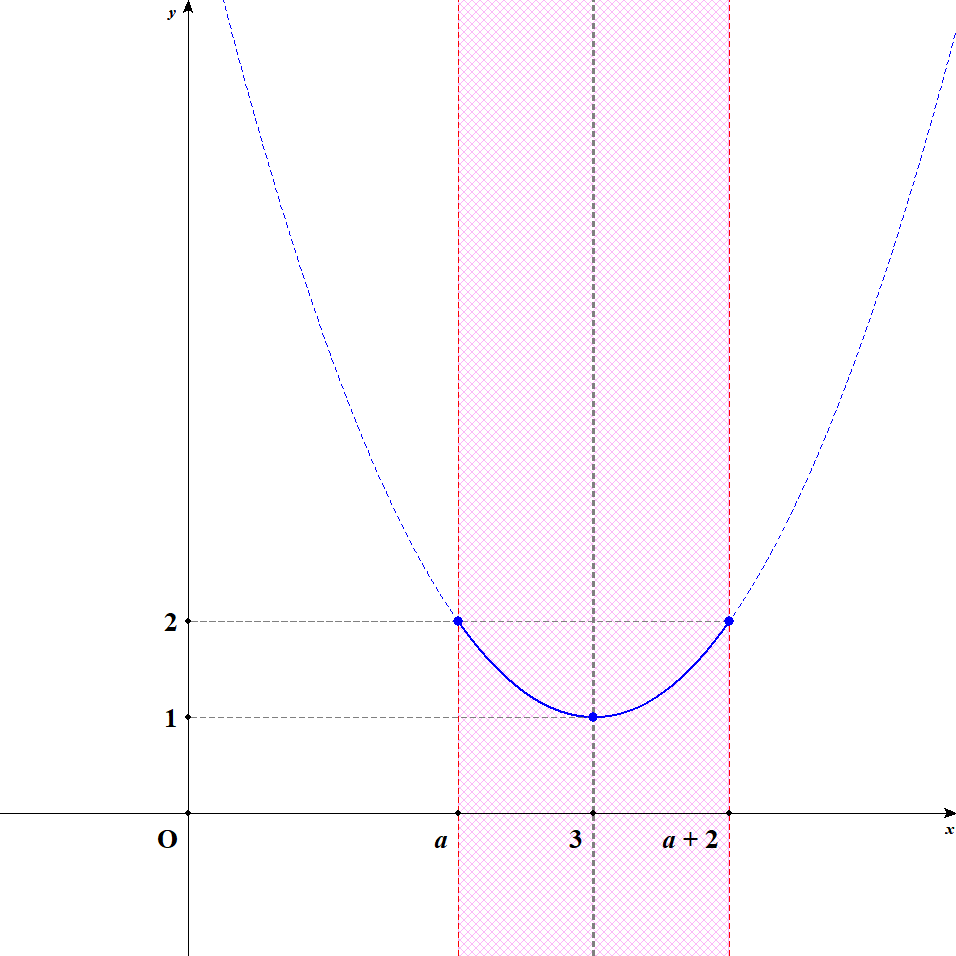
先に考えた通り，こうなるのは\(a = 2\)のときです。この場合，\(x = 2, 4\)のとき最大値\(2\)をとり，\(x = 3\)のとき最小値\(1\)をとります。

補足最大値

ここでは\(a = 2\)の場合を考えました。なので定義域の両端は\(x = 2, 4\)になりますし，最大値も\(a^2 - 6a + 10\)や\(a^2 - 2a + 2\)に\(a = 2\)を代入すれば\(2\)となることが分かります。

定義域がもう少し進むと，軸から定義域の右端までの距離が，左端までより遠くなります。このときのグラフは次のようになります。

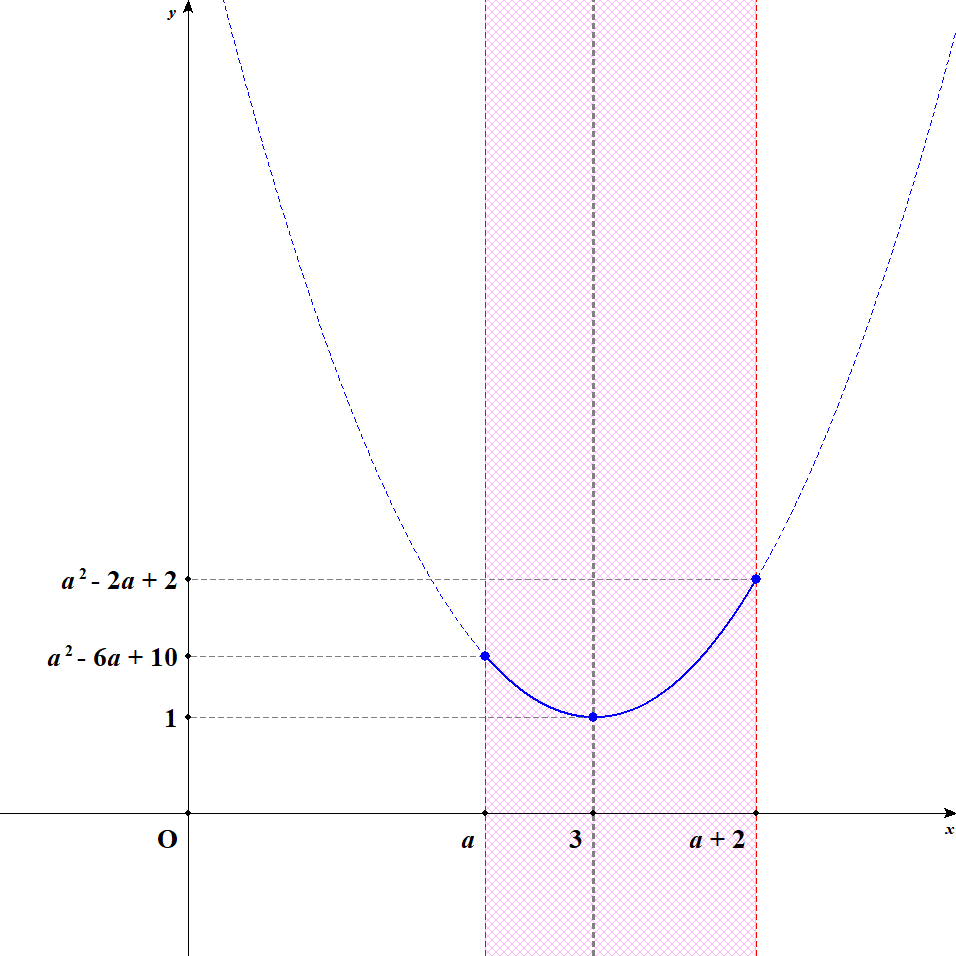
定義域が軸を完全に通り過ぎるまでは，定義域の右端で最大値をとり，頂点で最小値をとりますね。

つまり，\(2 < a \leqq 3\)であるうちは，\(x = a + 2\)のとき最大値\(a^2 - 2a + 2\)をとり，\(x = 3\)のとき最小値\(1\)をとります。

最後に定義域が軸を完全に通り過ぎた後を考えます。グラフは次のようになります。

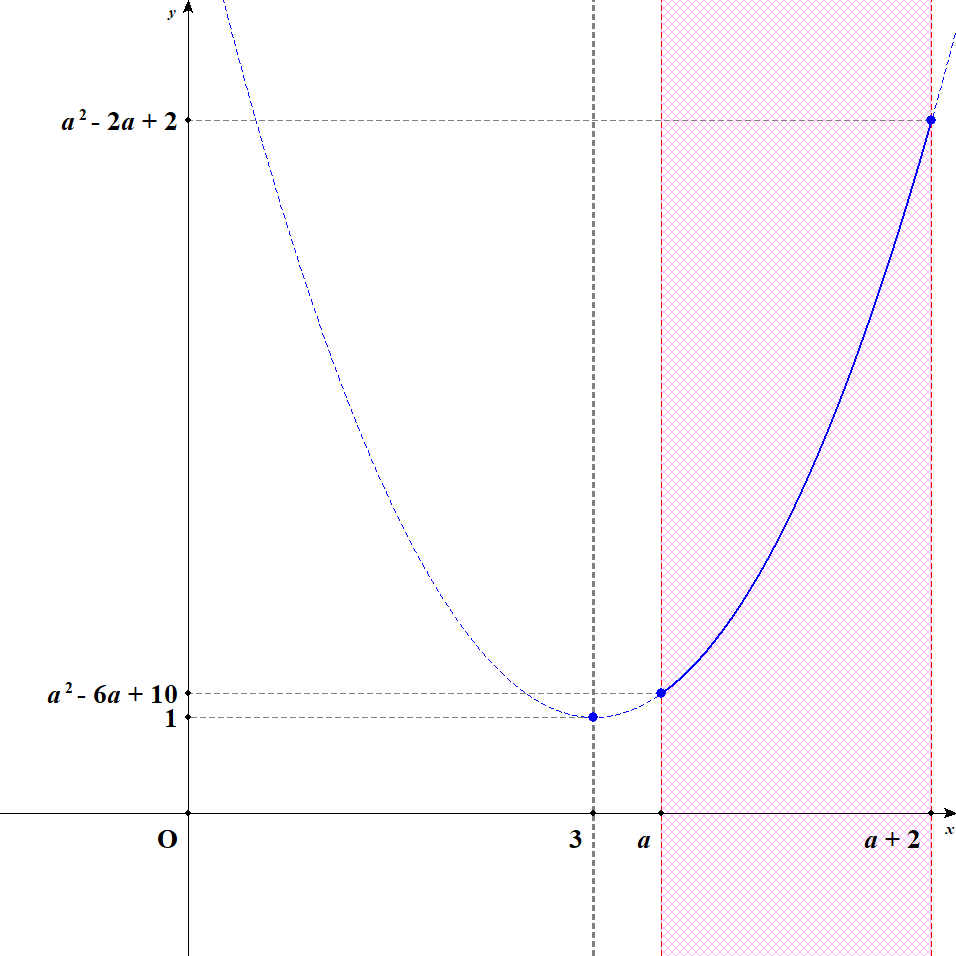
\(a > 3\)であるちは，\(x = a + 2\)のとき最大値\(a^2 - 2a + 2\)をとり，\(x = a\)のとき最小値\(a^2 - 6a + 10\)をとるわけですね。

以上をまとめると，この関数の最大値・最小値は次のようになります。

\(a\)の範囲	最大値	最小値
\(a < 1\)	\(x = a\)のとき \(a^2 - 6a + 10\)	\(x = a + 2\)のとき \(a^2 - 2a + 2\)
\(1 \leqq a < 2\)	\(x = a\)のとき \(a^2 - 6a + 10\)	\(x = 3\)のとき \(1\)
\(a = 2\)	\(x = 2, 4\)のとき \(2\)	\(x = 3\)のとき \(1\)
\(2 < a \leqq 3\)	\(x = a + 2\)のとき \(a^2 - 2a + 2\)	\(x = 3\)のとき \(1\)
\(a > 3\)	\(x = a + 2\)のとき \(a^2 - 2a + 2\)	\(x = a\)のとき \(a^2 - 6a + 10\)

もちろんこの場合も「軸が定義域の中にあるか外にあるか」と「軸が定義域の中にある場合，それが左寄り・真ん中・右寄りのどこにあるか」の２点を意識することが重要です。

ここまで全て下に凸の放物線を例にしてきましたが，上に凸の場合でも考え方は同じです。上に凸の場合の問題も確認問題にありますので，グラフや定義域が動くことをイメージしながら解いてみましょう。

確認問題

▲

\(a\)を\(a \neq 0\)を満たす定数とします。次の関数の最大値・最小値を求めてください。ただし，定義域を\(0 \leqq x \leqq 3\)とします。

\( \begin{align} y = ax^2 - 2ax \end{align} \)

答え

関数のグラフは\(a > 0\)のとき下に凸，\(a < 0\)のとき上に凸となりますね。まずは\(a > 0\)の場合を考えましょう。

関数の最大値・最小値を考える際には，軸と定義域の位置関係が重要です。まずは平方完成して，軸の位置をはっきりさせましょう。

\( \begin{align} y &= ax^2 - 2ax \\[5pt] &= a(x^2 - 2x) \\[5pt] &= a(x - 1)^2 - a \end{align} \)

このグラフの軸は\(x = 1\)ですね。グラフをかくと次のようになります。

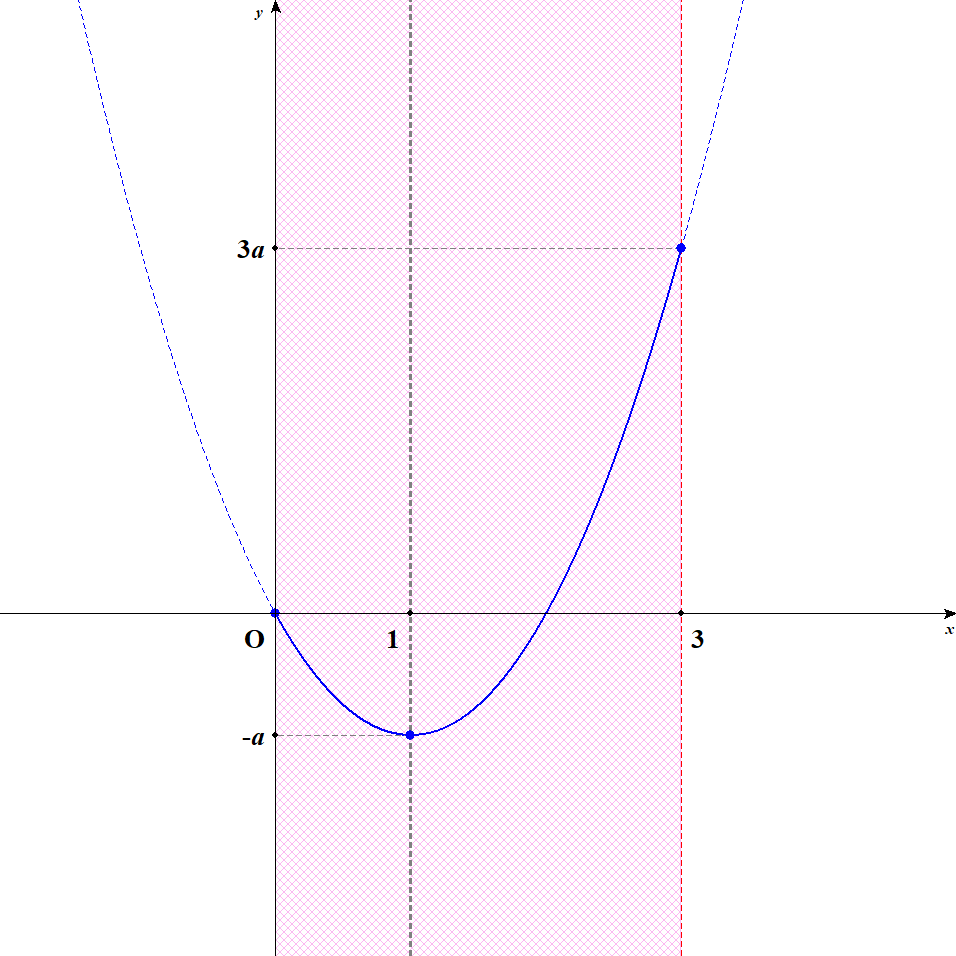
グラフから，\(x = 3\)のとき最大値\(3a\)をとり，\(x = 1\)のとき最小値\(-a\)をとることが分かります。

また，\(a < 0\)の場合の放物線は上に凸になるので，グラフは次のようになります。

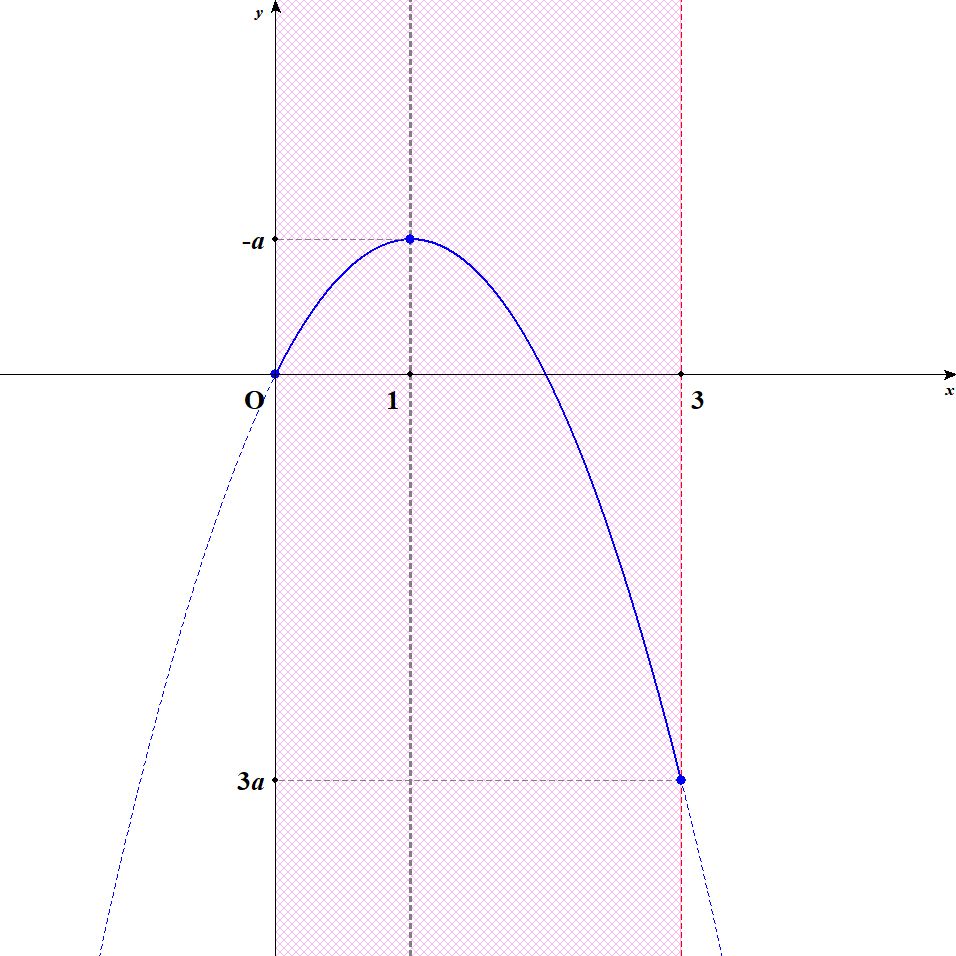
このときは，\(x = 1\)のとき最大値\(-a\)をとり，\(x = 3\)のとき最小値\(3a\)をとることが分かります。

以上から，この関数の最大値・最小値は次のようになります。

[1] \(a > 0\)の場合：
\(x = 3\)のとき最大値\(3a\)をとり，\(x = 1\)のとき最小値\(-a\)をとる。
[2] \(a < 0\)の場合：
\(x = 1\)のとき最大値\(-a\)をとり，\(x = 3\)のとき最小値\(3a\)をとる。

\(a\)を定数とします。次の関数の最大値・最小値を求めてください。ただし，定義域を\(2 \leqq x \leqq 4\)とします。

\( \begin{align} y = -x^2 + 4ax + 3 \end{align} \)

答え

まずは平方完成です。

\( \begin{align} y &= -x^2 + 4ax + 3 \\[5pt] &= -(x^2 - 4ax) + 3 \\[5pt] &= -(x - 2a)^2 + 4a^2 + 3 \end{align} \)

この関数のグラフは\(x = 2a\)を軸とする上に凸の放物線になるようです。最大値・最小値を求めるには，軸と定義域の位置関係を見ることが重要です。軸は定数\(a\)を含んでいますから，色々な値になり得ます。これを軸が動くと捉えて考えていきます。

上に凸の放物線では，軸から離れるほど値が小さくなることを意識しましょう。

[1] 軸が定義域の左外側にあるときを考えます。このとき\(2a < 2\)すなわち\(a < 1\)です。この状況では，\(x = 2\)のとき最大値\(8a - 1\)をとり，\(x = 4\)のとき最小値\(16a - 13\)をとります。

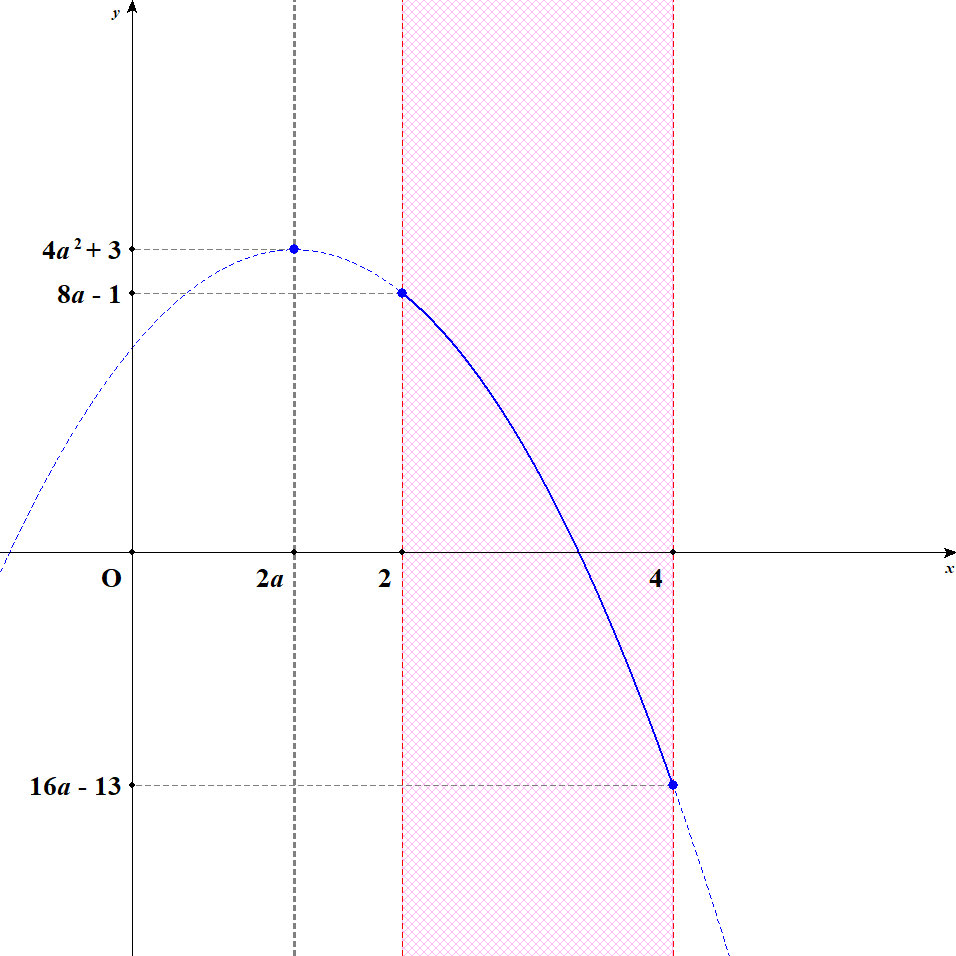
[2] 軸が定義域内の左寄りにあるときを考えます。このとき\(2 \leqq 2a < 3\)すなわち\(1 \leqq a < \displaystyle\frac{3}{2}\)です。この状況では，\(x = 2a\)のとき最大値\(4a^2 + 3\)をとり，\(x = 4\)のとき最小値\(16a - 13\)をとります。

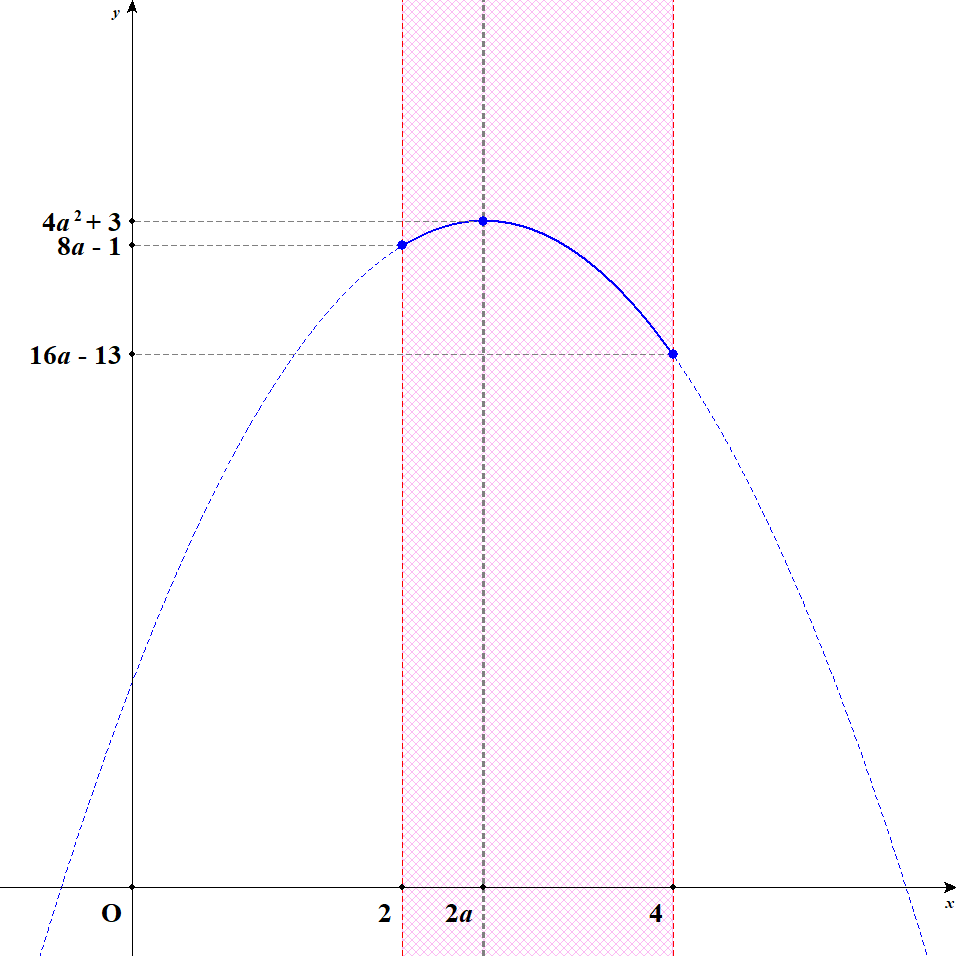
[3] 軸が定義域内の真ん中にあるときを考えます。このとき\(2a = 3\)すなわち\(a = \displaystyle\frac{3}{2}\)です。この状況では，\(x = 3\)のとき最大値\(12\)をとり，\(x = 2, 4\)のとき最小値\(11\)をとります。

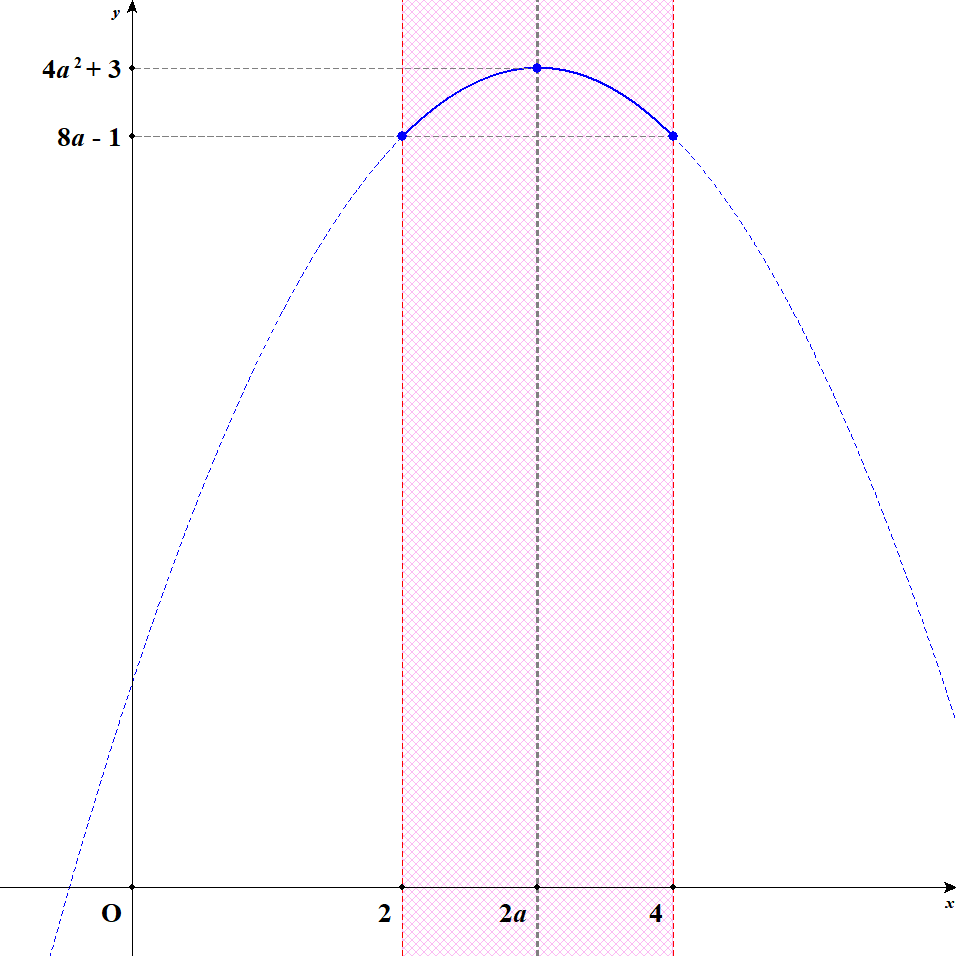
[4] 軸が定義域内の右寄りにあるときを考えます。このとき\(3 < 2a \leqq 4\)すなわち\(\displaystyle\frac{3}{2} < a \leqq 2\)です。この状況では，\(x = 2a\)のとき最大値\(4a^2 + 3\)をとり，\(x = 2\)のとき最小値\(8a - 1\)をとります。

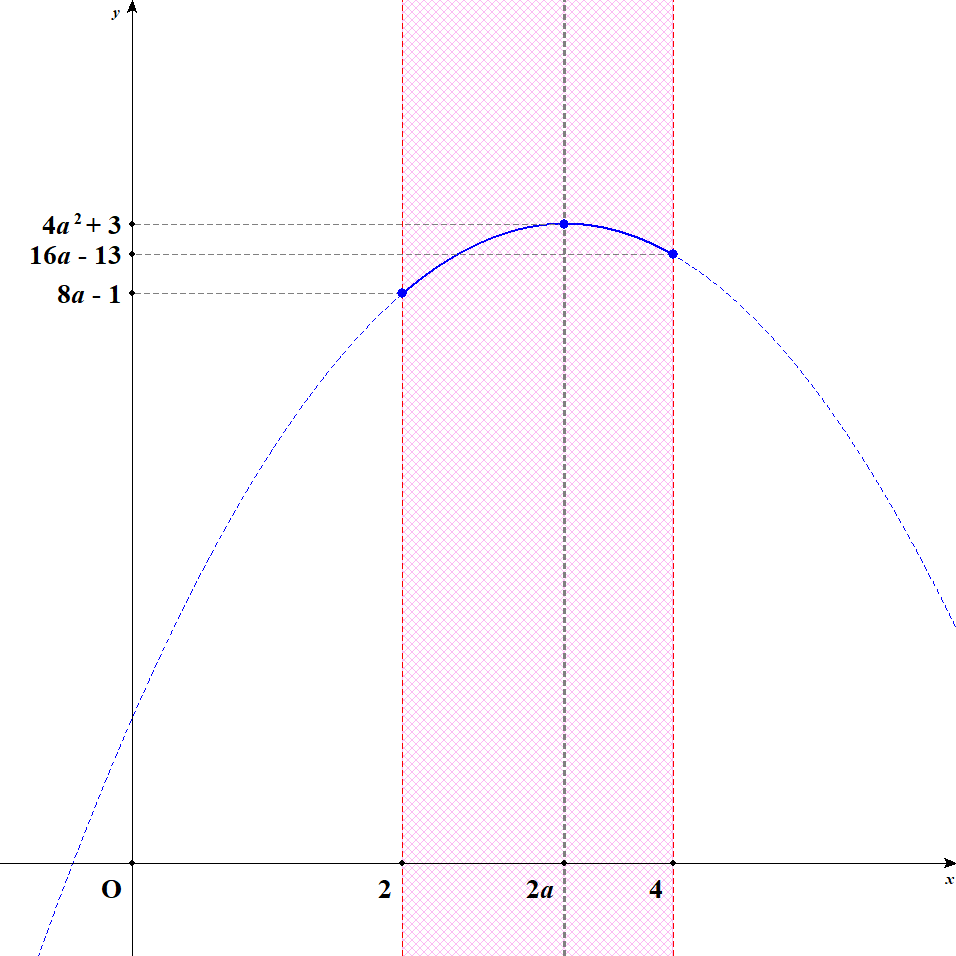
[5] 軸が定義域の右外側にあるときを考えます。このとき\(2a > 4\)すなわち\(a > 2\)です。この状況では，\(x = 4\)のとき最大値\(16a - 13\)をとり，\(x = 2\)のとき最小値\(8a - 1\)をとります。

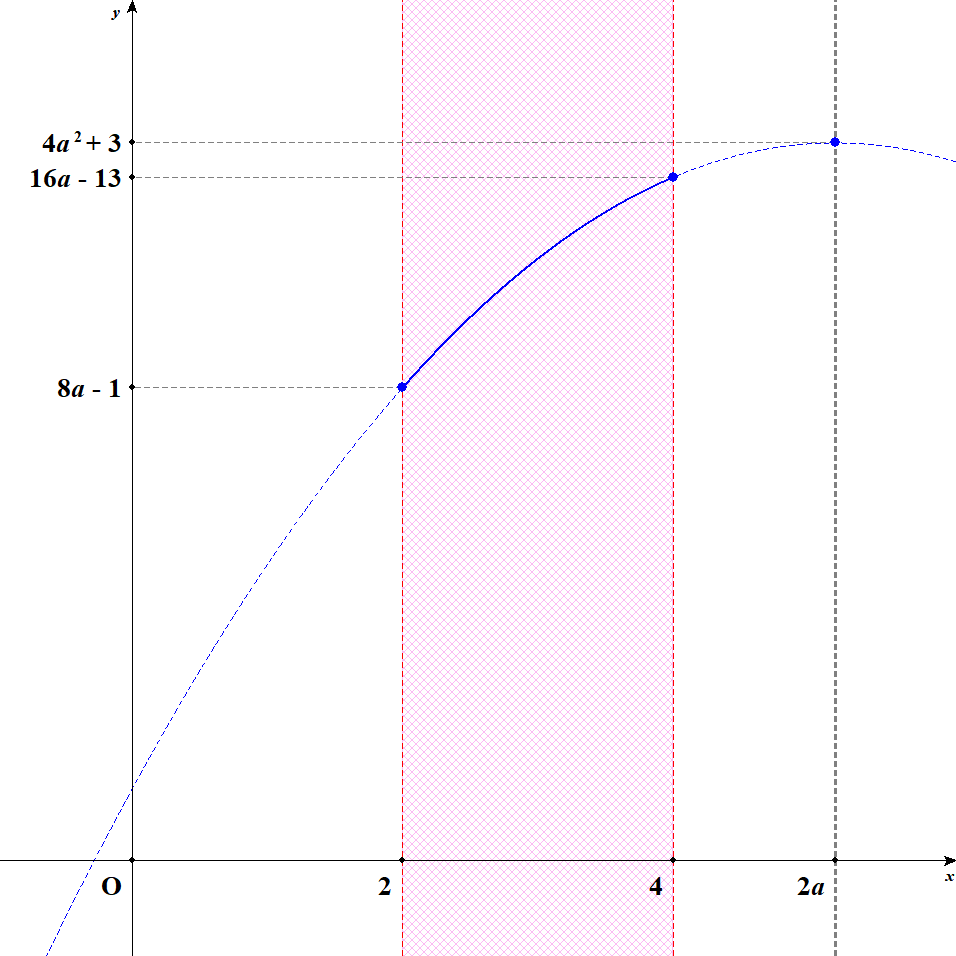
以上から，この関数の最大値・最小値は次のようになります。

[1] \(a < 1\)の場合：
\(x = 2\)のとき最大値\(8a - 1\)をとり，\(x = 4\)のとき最小値\(16a - 13\)をとる。
[2] \(1 \leqq a < \displaystyle\frac{3}{2}\)の場合：
\(x = 2a\)のとき最大値\(4a^2 + 3\)をとり，\(x = 4\)のとき最小値\(16a - 13\)をとる。
[3] \(a = \displaystyle\frac{3}{2}\)の場合：
\(x = 3\)のとき最大値\(12\)をとり，\(x = 2, 4\)のとき最小値\(11\)をとる。
[4] \(\displaystyle\frac{3}{2} < a \leqq 2\)の場合：
\(x = 2a\)のとき最大値\(4a^2 + 3\)をとり，\(x = 2\)のとき最小値\(8a - 1\)をとる。
[5] \(a > 2\)の場合：
\(x = 4\)のとき最大値\(16a - 13\)をとり，\(x = 2\)のとき最小値\(8a - 1\)をとる。

\(a\)を\(a < 2\)を満たす定数とします。次の関数の最大値・最小値を求めてください。ただし，定義域を\(a \leqq x \leqq 2\)とします。

\( \begin{align} y = 2x^2 + 4x - 1 \end{align} \)

答え

まずは平方完成です。

\( \begin{align} y &= 2x^2 + 4x - 1 \\[5pt] &= 2(x^2 + 2x) - 1 \\[5pt] &= 2(x + 1)^2 - 3 \end{align} \)

このグラフは\(x = -1\)を軸とする放物線ですね。この問題では，軸の位置は動きませんが，定義域の左端が伸び縮みします。狭い定義域から考えて，徐々に拡げていってみましょう。

[1] 軸が定義域の左外側にあるときを考えます。このとき\(-1 < a < 2\)です。この状況では，\(x = 2\)のとき最大値\(15\)をとり，\(x = a\)のとき最小値\(2a^2 + 4a - 1\)をとります。

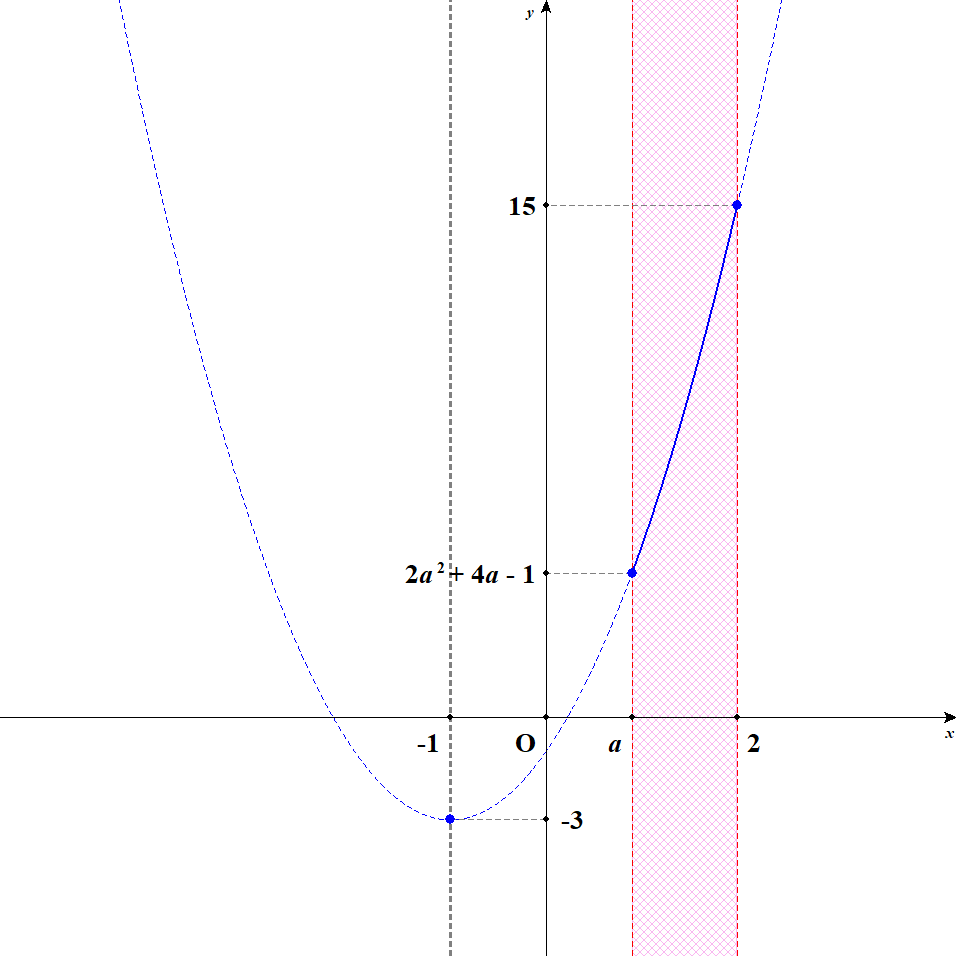
[2] 軸が定義域内の左寄りにあるときを考えます。このとき\(-4 < a \leqq -1\)です。 \(a = -4\)までいくと軸の\(x = -1\)が定義域の真ん中になってしまいますね。この状況では，\(x = 2\)のとき最大値\(15\)をとり，\(x = -1\)のとき最小値\(-3\)をとります。

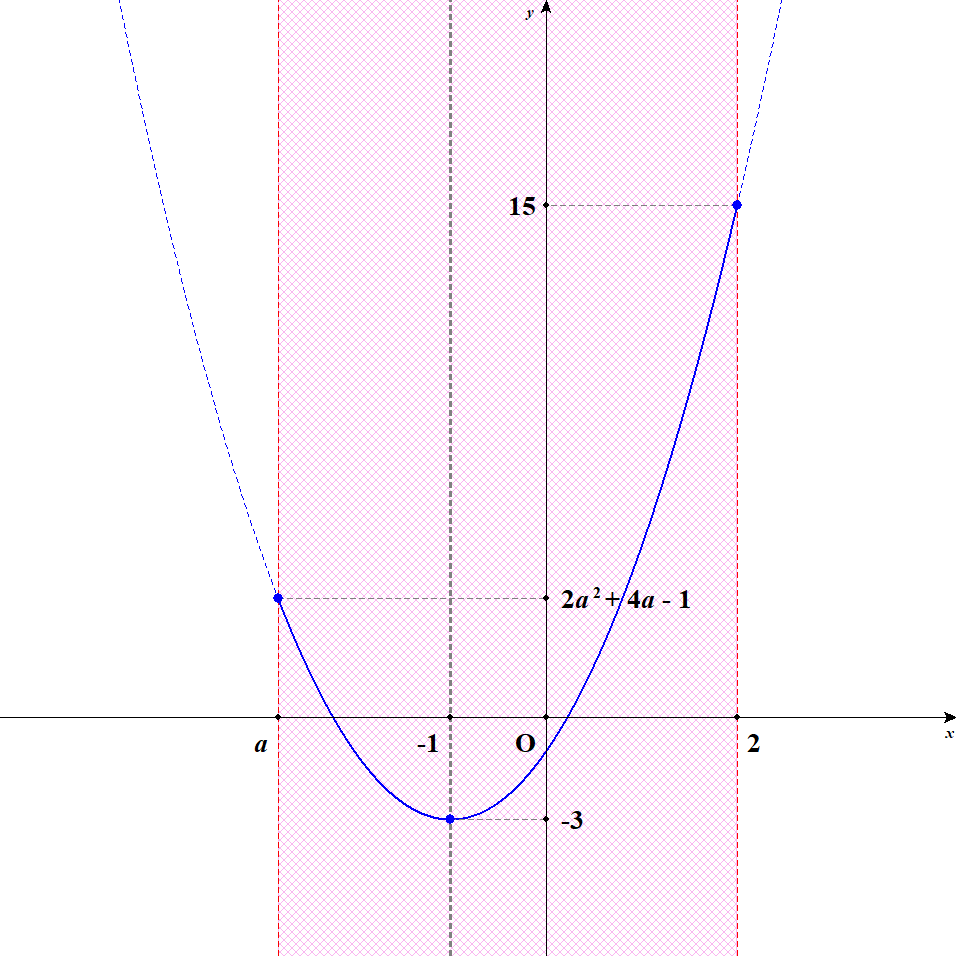
[3] 軸が定義域内の真ん中にあるときを考えます。このとき\(a = -4\)です。軸から定義域の左端までの距離が，右端までの距離と等しくなる\(a\)の値ですね。この状況では，\(x = -4, 2\)のとき最大値\(15\)をとり，\(x = -1\)のとき最小値\(-3\)をとります。

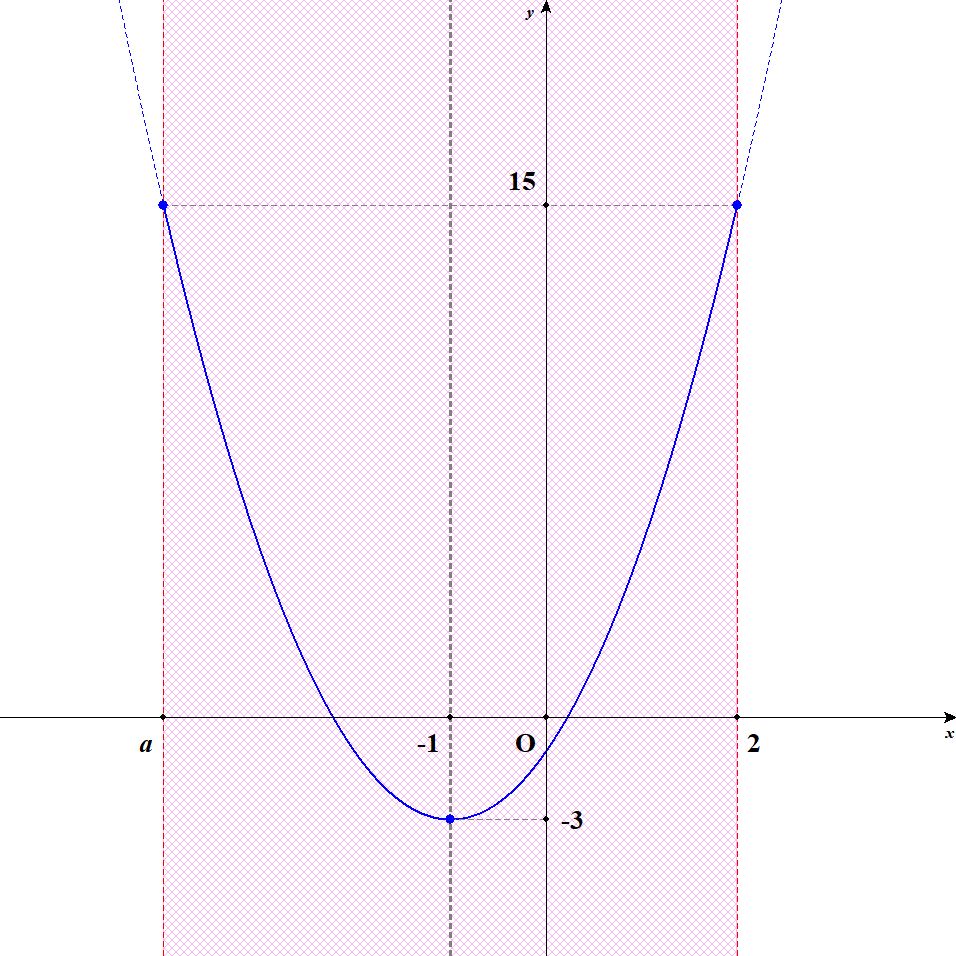
[4] 軸が定義域内の右寄りにあるときを考えます。このとき\(a < -4\)です。この状況では，\(x = a\)のとき最大値\(2a^2 + 4a - 1\)をとり，\(x = -1\)のとき最小値\(-3\)をとります。

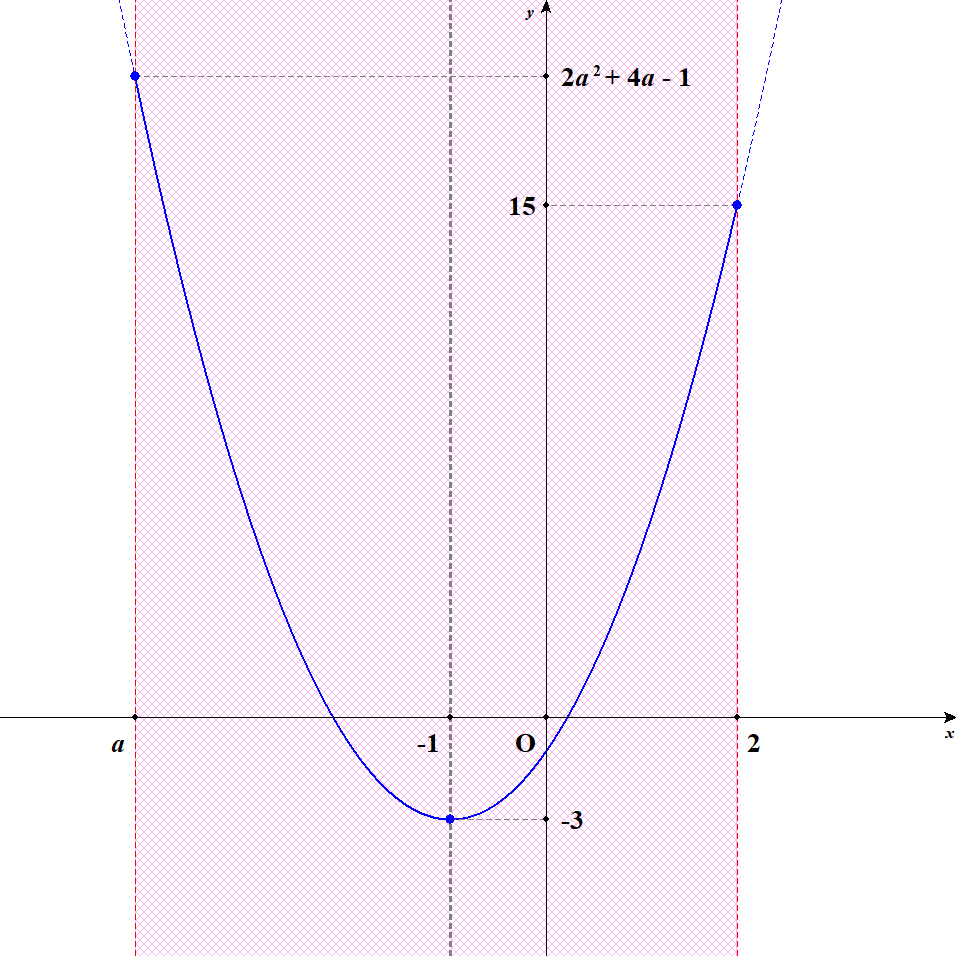
以上から，この関数の最大値・最小値は次のようになります。

[1] \(-1 < a < 2\)の場合：
\(x = 2\)のとき最大値\(15\)をとり，\(x = a\)のとき最小値\(2a^2 + 4a - 1\)をとる。
[2] \(-4 < a \leqq -1\)の場合：
\(x = 2\)のとき最大値\(15\)をとり，\(x = -1\)のとき最小値\(-3\)をとる。
[3] \(a = -4\)の場合：
\(x = -4, 2\)のとき最大値\(15\)をとり，\(x = -1\)のとき最小値\(-3\)をとる。
[4] \(a < -4\)の場合：
\(x = a\)のとき最大値\(2a^2 + 4a - 1\)をとり，\(x = -1\)のとき最小値\(-3\)をとる。

\(a\)を\(a < 0\)を満たす定数とします。次の関数の最大値・最小値を求めてください。ただし，定義域を\(2a \leqq x \leqq a\)とします。

\( \begin{align} y = -x^2 - 8x + 2a \end{align} \)

答え

まずは平方完成です。

\( \begin{align} y &= -x^2 - 8x + 2a \\[5pt] &= -(x^2 + 8x) + 2a \\[5pt] &= -(x + 4)^2 + 2a + 16 \end{align} \)

このグラフは\(x = -4\)を軸とする放物線ですね。この問題では，軸の位置は動きませんが，定義域の位置が動きます。 \(a\)を小さくしていくと，定義域は左に動いていきますね。定義域が右の方にある場合から考えて，徐々に左に動かしていってみましょう。

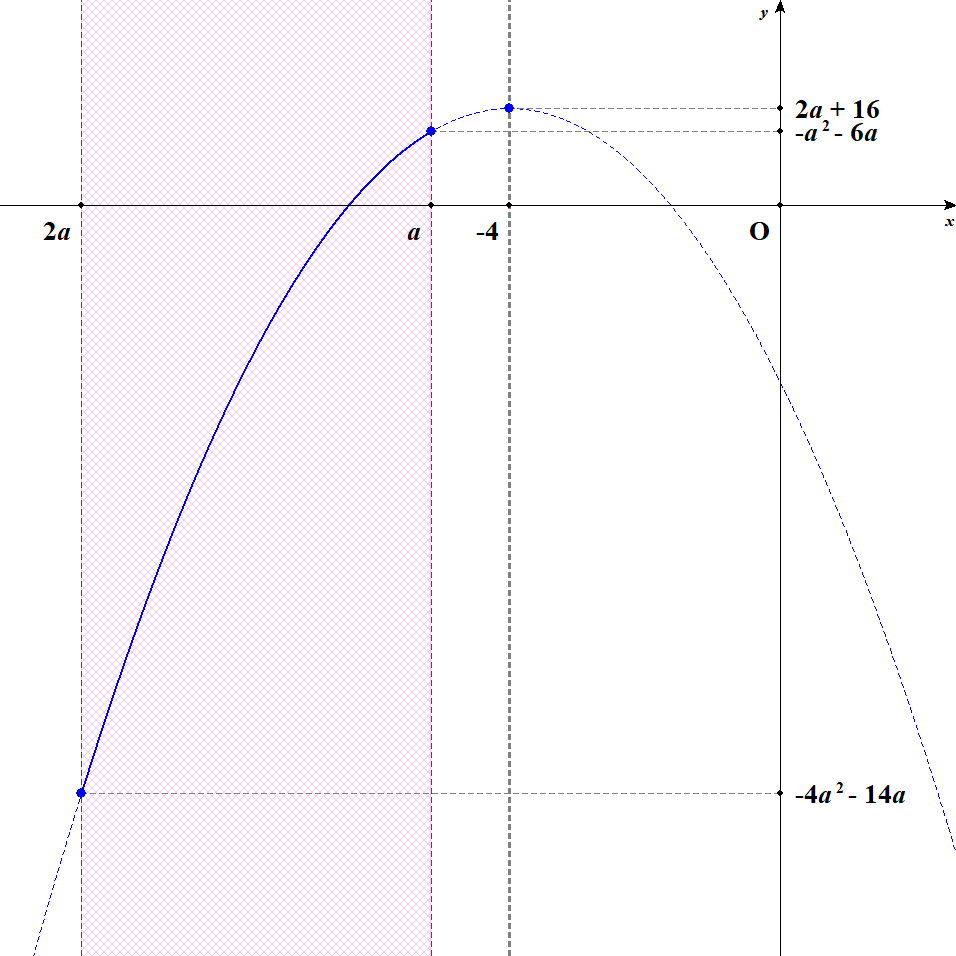
[1] 軸が定義域の左外側にある場合を考えます。このとき\(-4 < 2a\)すなわち\(-2 < a < 0\)です。 \(a < 0\)は問題の条件です。この状況では，\(x = 2a\)のとき最大値\(-4a^2 - 14a\)をとり，\(x = a\)のとき最小値\(-a^2 - 6a\)をとります。

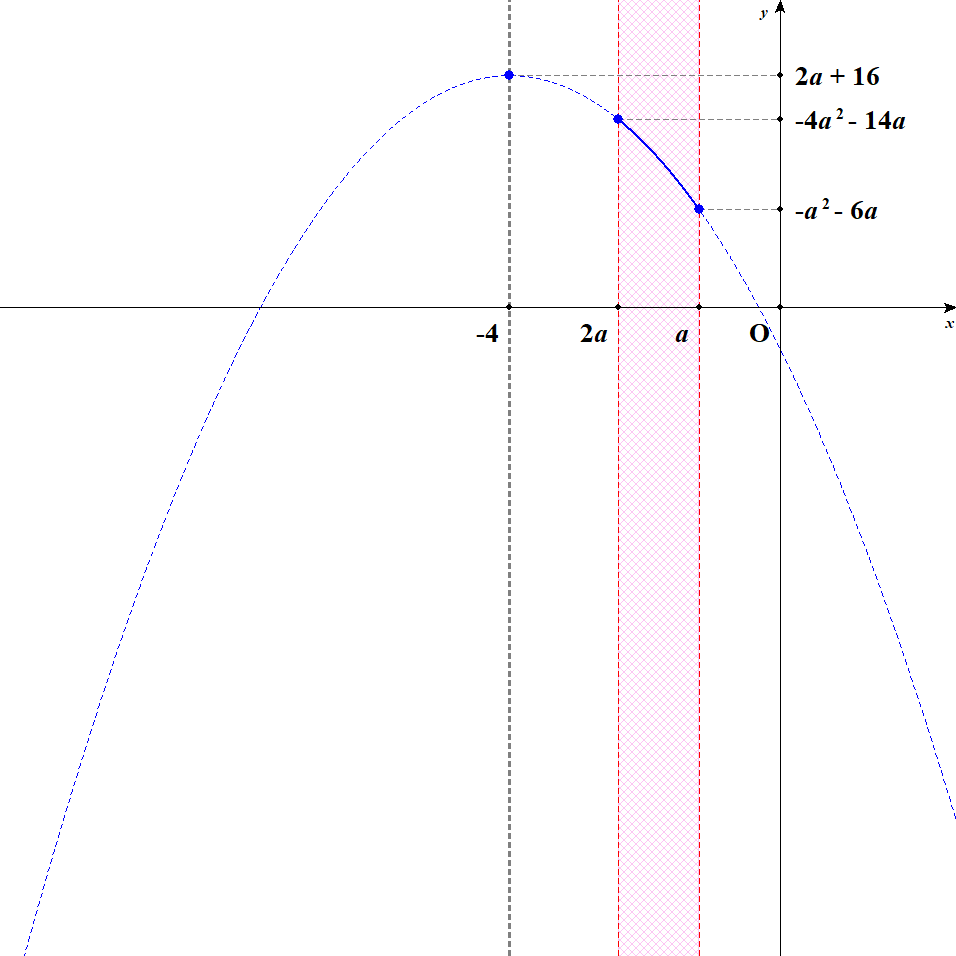
[2] 軸が定義域内の左寄りにある場合を考えます。軸がちょうど定義域の真ん中になるのは，\(\displaystyle\frac{2a + a}{2} = -4\)すなわち\(a = -\displaystyle\frac{8}{3}\)のときですが，その手前までが軸が左寄りになる場合です。このとき\(2a \leqq -4\)かつ\(-\displaystyle\frac{8}{3} < a\)，すなわち\(-\displaystyle\frac{8}{3} < a \leqq -2\)です。この状況では，\(x = -4\)のとき最大値\(2a + 16\)をとり，\(x = a\)のとき最小値\(-a^2 - 6a\)をとります。

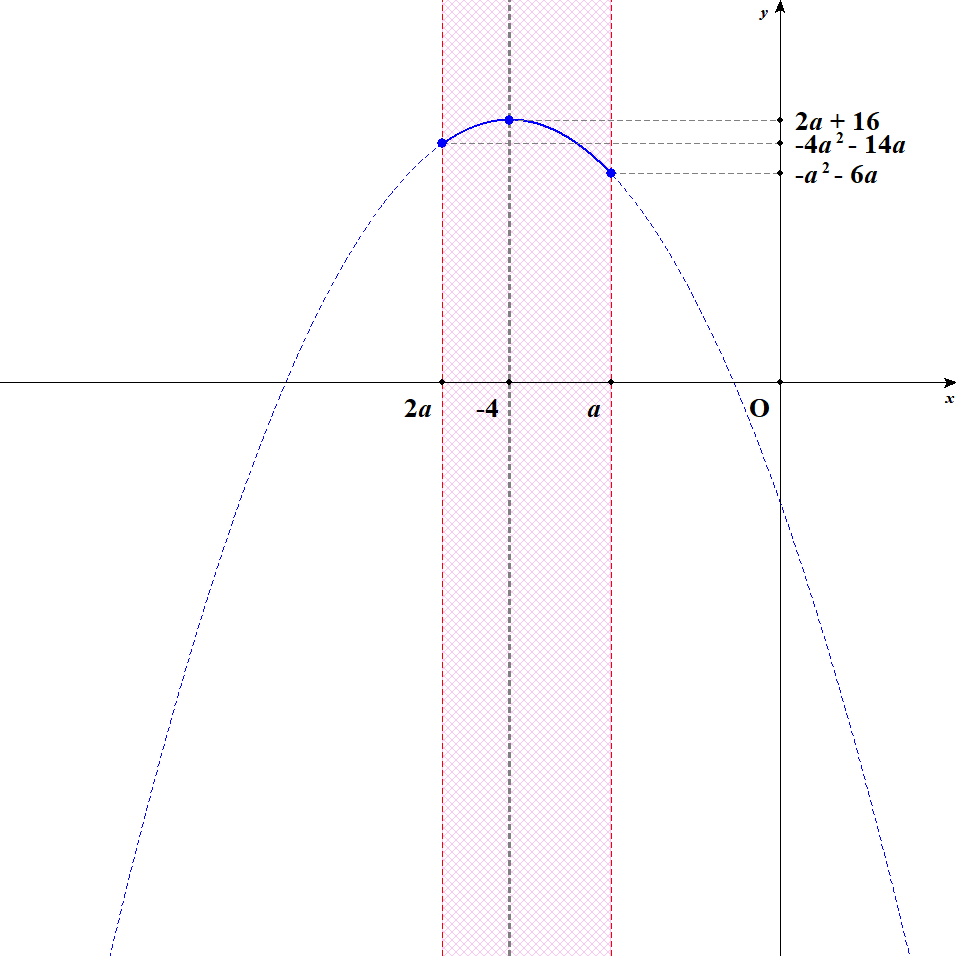
[3] 軸が定義域内の真ん中にある場合を考えます。このとき，上で考えた通り\(a = -\displaystyle\frac{8}{3}\)です。この状況では，\(x = -4\)のとき最大値\(\displaystyle\frac{32}{3}\)をとり，\(x = -\displaystyle\frac{16}{3}, -\displaystyle\frac{8}{3}\)のとき最小値\(\displaystyle\frac{80}{9}\)をとります。

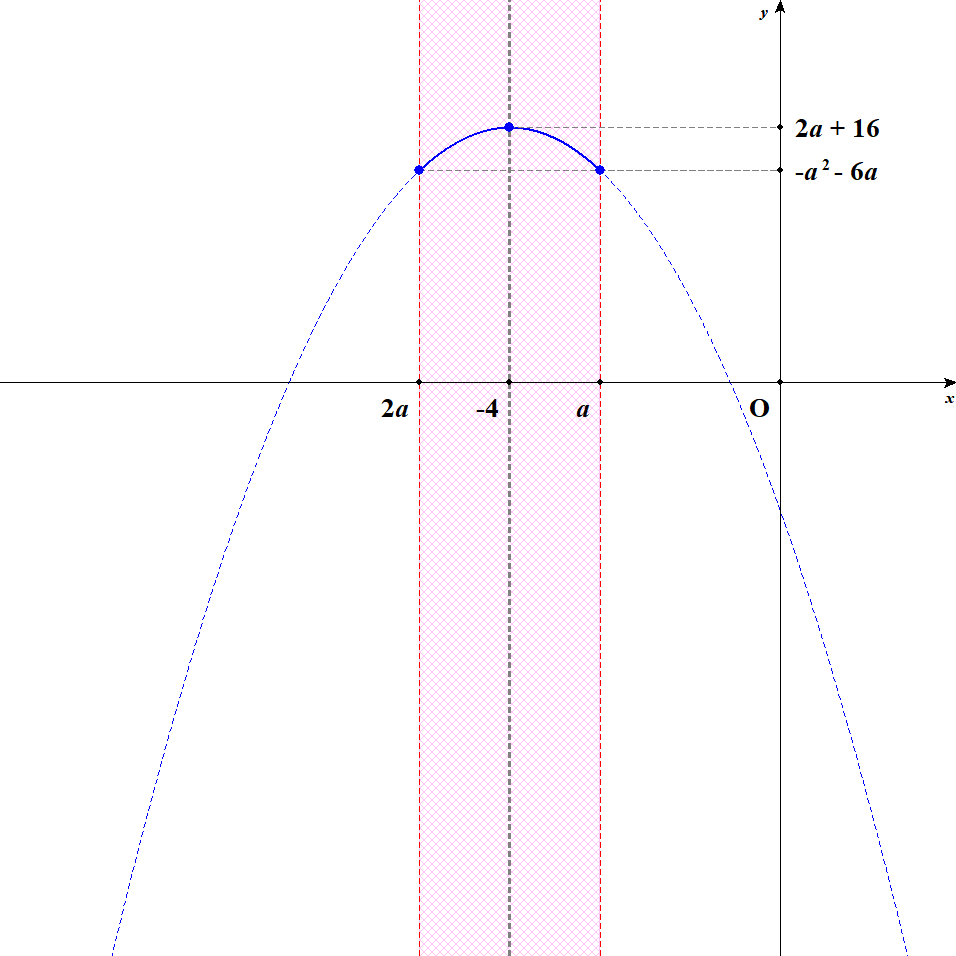
[4] 軸が定義域内の右寄りにある場合を考えます。このとき\(a < -\displaystyle\frac{8}{3}\)かつ\(-4 \leqq a\)，すなわち\(-4 \leqq a < -\displaystyle\frac{8}{3}\)です。この状況では，\(x = -4\)のとき最大値\(2a + 16\)をとり，\(x = 2a\)のとき最小値\(-4a^2 - 14a\)をとります。

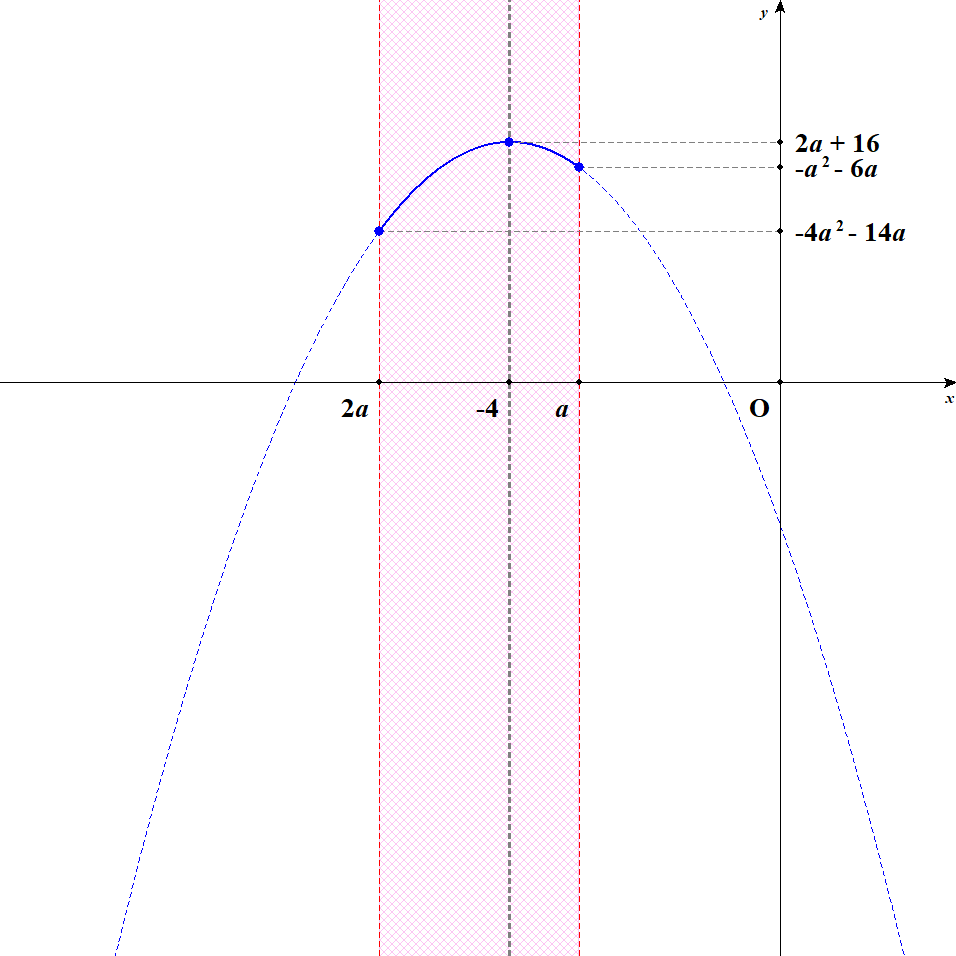
[5] 軸が定義域の右外側にある場合を考えます。このとき\(a < -4\)です。この状況では，\(x = a\)のとき最大値\(-a^2 - 6a\)をとり，\(x = 2a\)のとき最小値\(-4a^2 - 14a\)をとります。

以上から，この関数の最大値・最小値は次のようになります。

[1] \(-2 < a < 0\)の場合：
\(x = 2a\)のとき最大値\(-4a^2 - 14a\)をとり，\(x = a\)のとき最小値\(-a^2 - 6a\)をとる。
[2] \(-\displaystyle\frac{8}{3} < a \leqq -2\)の場合：
\(x = -4\)のとき最大値\(2a + 16\)をとり，\(x = a\)のとき最小値\(-a^2 - 6a\)をとる。
[3] \(a = -\displaystyle\frac{8}{3}\)の場合：
\(x = -4\)のとき最大値\(\displaystyle\frac{32}{3}\)をとり，\(x = -\displaystyle\frac{16}{3}, -\displaystyle\frac{8}{3}\)のとき最小値\(\displaystyle\frac{80}{9}\)をとる。
[4] \(-4 \leqq a < -\displaystyle\frac{8}{3}\)の場合：
\(x = -4\)のとき最大値\(2a + 16\)をとり，\(x = 2a\)のとき最小値\(-4a^2 - 14a\)をとる。
[5] \(a < -4\)の場合：
\(x = a\)のとき最大値\(-a^2 - 6a\)をとり，\(x = 2a\)のとき最小値\(-4a^2 - 14a\)をとる。

\(a\)を定数として，次の関数を考えます。ただし，定義域を\(1 \leqq x \leqq 3\)とします。

\( \begin{align} y = x^2 - 2ax + 4a + 6 \end{align} \)

この関数の最小値を\(m(a)\)とします。 \(m(a)\)の値は\(a\)の値によって色々変わります。横軸を\(a\)，縦軸を\(m(a)\)とするグラフをかき，\(m(a)\)の最大値を求めてください。

答え

いつも通り平方完成から始めます。

\( \begin{align} y &= x^2 - 2ax + 4a + 6 \\[5pt] &= (x - a)^2 - a^2 + 4a + 6 \end{align} \)

このグラフは\(x = a\)を軸とする放物線ですね。まずはこの関数の定義域\(1 \leqq x \leqq 3\)における最小値\(m(a)\)を求めます。軸が左の方から右に向かって動くことをイメージして，順に考えていきます。

今回は前半のグラフは省略します。次のことに気を付けて解説を読んでください。下に凸の放物線の最小値の求め方についてです。

最小値は，軸が定義域の中にある場合，頂点でとる。
最小値は，軸が定義域の外にある場合，定義域の端のうち，軸から近い方でとる。

[1] 軸が定義域の左外側にある場合を考えます。このとき\(a < 1\)です。この状況では，\(x = 1\)のとき最小値\(2a + 7\)をとります。

[2] 軸が定義域内にある場合を考えます。このとき\(1 \leqq a \leqq 3\)です。この状況では，\(x = a\)のとき最小値\(-a^2 +4a + 6\)をとります。

[3] 軸が定義域の右外側にある場合を考えます。このとき\(a > 3\)です。この状況では，\(x = 3\)のとき最小値\(-2a + 15\)をとります。

以上から，\(m(a)\)が次のような関数であることが分かりました。

\( \begin{eqnarray} m(a) = \left\{ \begin{array}{l} 2a + 7 & (a < 1) \\ -a^2 + 4a + 6 & (1 \leqq a \leqq 3) \\ -2a + 15 & (a > 3) \end{array} \right. \end{eqnarray} \)

\(m(a)\)のグラフをかいてみましょう。そのために，まずは\(-a^2 + 4a + 6\)の平方完成をしておきます。

\( \begin{align} m(a) &= -a^2 + 4a + 6 \\[5pt] &= -(a^2 - 4a) + 6 \\[5pt] &= -(a - 2)^2 + 10 \end{align} \)

グラフは，\(a < 1\)の範囲では直線\(m(a) = 2a + 7\)を，\(1 \leqq a \leqq 3\)の範囲では放物線\(m(a) = -a^2 + 4a + 6\)を，\(a > 3\)の範囲では直線\(m(a) = -2a + 15\)をかけば良いですね。グラフは次のようになります。

グラフから，\(m(a)\)は，\(a = 2\)のとき最大値\(10\)をとることが分かりました。