２次関数の応用問題

はじめに

前回までで２次関数の色々な問題を解けるようになったので，今回は２次関数の知識を利用できる応用問題を考えてみましょう。

試しにひとつ

▼

応用問題とはいっても，やることは「問題の状況を数式で表す」と「数式について調べる」の２つだけです。後者は前回までで学習しましたね。今回は応用問題をひとつ解いてみて，前者も実践してみましょう。

次の定番問題を考えます。

【問題】長さ\(80\)[\(\mathrm{cm}\)]の針金を２つに切って，２つの正方形を作ります。この２つの正方形の面積の和を最小にしたいとき，針金をどのように切れば良いでしょうか？

こういった文章題を考えるとき，問題の状況を数式で表すのですが，次の３つのことに注意しましょう。

計算が楽になるように文字を使う
使う文字の種類はなるべく少なくする
文字についての条件を見落とさない

まず何を文字でおくか考えます。例えば切った後の針金の長さを\(x\)[\(\mathrm{cm}\)]，\(y\)[\(\mathrm{cm}\)]と表すことが思いつきます。もちろんこれで考えていくことも可能ですが，２つの改善点があります。

ひとつは，何を文字でおくかを変えることです。今のままだと，正方形の面積は\(\displaystyle\frac{x}{4} \times \displaystyle\frac{x}{4} = \displaystyle\frac{x^2}{16}\)[\(\mathrm{cm}^{2}\)]となり，分数が出てくるのがちょっと嫌です。（気にならなければ良いですが。）代わりに正方形の一辺の長さを\(x\)[\(\mathrm{cm}\)]とすれば，面積は\(x^2\)[\(\mathrm{cm}^{2}\)]と簡単な式になります。

もうひとつは，使う文字の数を減らすことです。上のように，片方の正方形の一辺の長さを\(x\)[\(\mathrm{cm}\)]とすれば，その針金の長さは\(4x\)[\(\mathrm{cm}\)]です。ということは，もう一方の針金の長さは\(80 - 4x\)[\(\mathrm{cm}\)]であり，正方形の一辺の長さは\(20 - x\)[\(\mathrm{cm}\)]になります。 \(y\)という新しい文字を使う必要はないわけです。

次に\(x\)に関する条件を考える必要があります。例えば\(x = -1\)なんかは絶対にあり得ませんよね。また，元の針金の長さが\(80\)[\(\mathrm{cm}\)]ですから，\(x = 100\)もあり得ません。

切った後の針金の長さは\(0\)[\(\mathrm{cm}\)]より大きく\(80\)[\(\mathrm{cm}\)]より小さい必要があるので，次の条件が必要です。

\( \begin{align} 0 < 4x < 80 \end{align} \)

これを解くと\(0 < x < 20\)です。これが\(x\)の定義域になります。

補足 \(0 < 80 - 4x < 80\)は？

切った後の針金は２つあります。もう一方の針金の長さ\(80 - 4x\)に関する条件\(0 < 80 - 4x < 80\)は必要ないのでしょうか？

\(0 < 4x < 80\)という条件さえあれば，これは特に必要ありません。片方の針金の長さが正常なら，その針金は正常に切り取れているわけですから，残ったもう一方の針金の長さも正常なのです。

\(x\)の定義域も分かりましたから，後は２つの正方形の面積の和を\(x\)の式で表して，その最小値を求めるだけです。２つの正方形の面積の和を\(y\)[\(\mathrm{cm}^{2}\)]とすると，\(y\)は次のように表せます。

\( \begin{align} y &= x^2 + (20 - x)^2 \\[5pt] &= x^2 + 400 - 40x + x^2 \\[5pt] &= 2x^2 - 40x + 400 \\[5pt] &= 2(x^2 - 20x) + 400 \\[5pt] &= 2(x - 10)^2 + 200 \end{align} \)

このグラフは次のようになります。

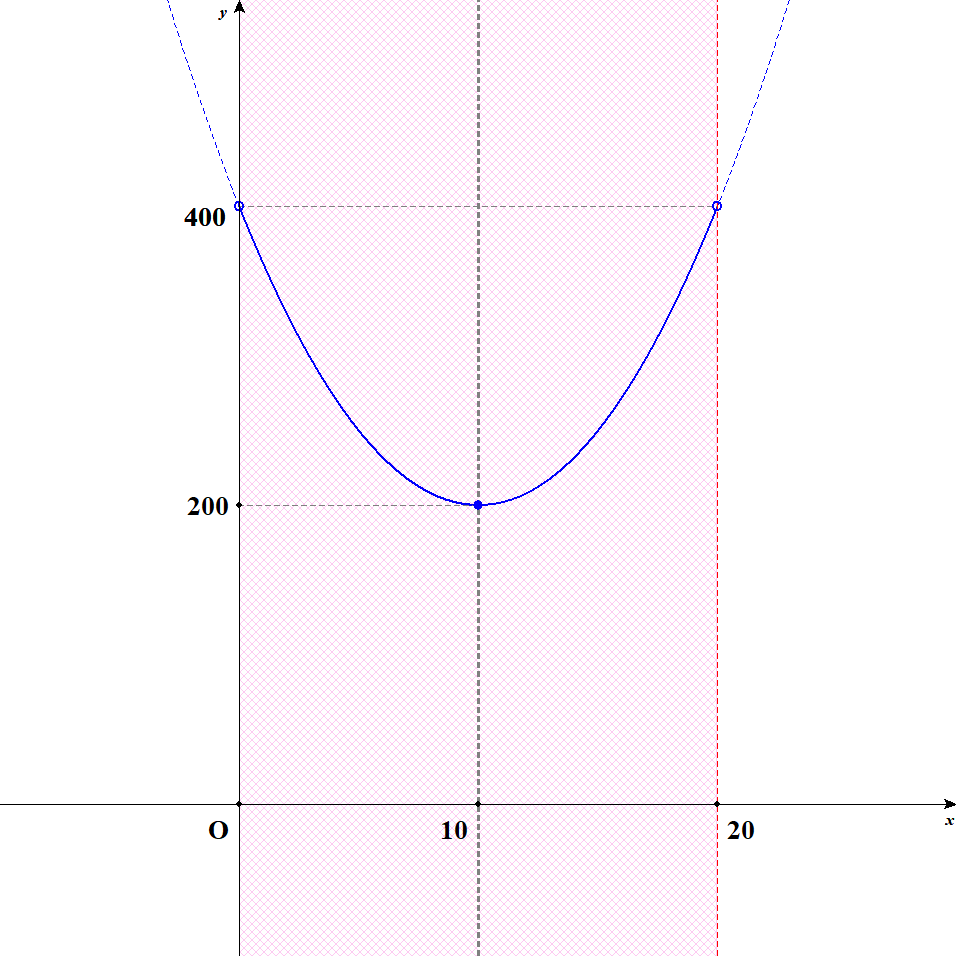
グラフから，この関数は\(x = 10\)のとき最小値\(200\)をとることが分かります。このとき２つの針金の長さは\(4x = 40\)[\(\mathrm{cm}\)]と\(80 - 4x = 40\)[\(\mathrm{cm}\)]です。

以上から，題意を満たすためには，２つの針金を同じ長さに切れば良いことが分かりました。

確認問題で他の問題にも挑戦してみてください。

確認問題

▲

\(N\)さんは商品\(A\)を売っています。現在，\(A\)の単価は\(500\)円で，ひと月に\(12000\)個売れます。 \(N\)さんはこの売上高に満足しておらず，\(A\)の単価を調整したいと考えています。単価を上げれば需要は減少し，単価を下げれば需要は増加します。

今までの経験から，\(A\)の売れる個数は，単価を\(1\)円上げるごとに\(30\)個減少し，\(1\)円下げるごとに\(30\)個増加することがわかっています。ひと月の売上高を最大化するには，\(A\)の単価をいくらに設定すれば良いでしょうか？売上高は「単価\(\times\)売れた個数」で求められます。

答え

\(A\)の単価を\(x\)円とおきます。単価ですから\(x > 0\)であり，これが\(x\)の定義域ですね。

このとき，\(A\)の値上げ額は\(x - 500\)円です。これが負の場合は値下げですね。このとき，\(A\)の売れる個数は\(30(x - 500)\)減少します。これが負の場合は増加ですね。

以上から，\(A\)の単価が\(x\)円のときのひと月の売上高を\(y\)円とすると，\(y\)は次のようになります。

\( \begin{align} y &= x \{12000 - 30(x - 500)\} \\[5pt] &= x(12000 - 30x + 15000) \\[5pt] &= -30x^2 + 27000x \\[5pt] &= -30(x^2 - 900x) \\[5pt] &= -30(x - 450)^2 + 30 \cdot 450^2 \end{align} \)

このグラフは\(x = 450\)を軸とする上に凸の放物線です。定義域は\(x > 0\)で，軸が定義域に含まれていますから，グラフをかくまでもなく\(x = 450\)のとき最大値をとることが分かります。

以上から，売上高を最大化する\(A\)の単価は\(450\)円でした。今までは単価が高すぎて買ってくれる人が少なかったんですね。

動物園のオーナーである\(Z\)さんは，園内の余っているスペースを有効活用したいです。現在，下図のように壁に囲まれた角の部分に空きスペースがあります。ただし，これは上空から見下ろした図であり，この角は直角です。

\(Z\)さんは，このスペースに下図のようにフェンスを設置することで，動物たちの過ごす空間を確保しようと考えました。壁とフェンスで囲まれた空間です。ただし，予算がないため，フェンスは長さ\(8\)[\(\mathrm{m}\)]のものひとつしか用意できませんでした。

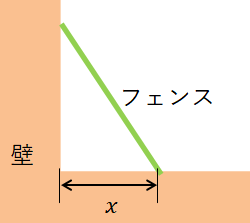
動物たちの過ごす空間をなるべく広く確保するためには，フェンスをどのように設置すれば良いでしょうか？壁からフェンスの一端までの距離を\(x\)[\(\mathrm{m}\)]として，この\(x\)の値をいくつにすれば良いかで答えてください。

【注１】動物たちが逃げないように，フェンスの両端は必ず壁に接するようにしてください。フェンスを切ったり折ったりもしません。

【注２】\(a > 0, \ b > 0\)のとき，\(a \leqq b\)と\(a^2 \leqq b^2\)が同値であることを使っても良いです。

答え

壁とフェンスに囲まれた空間は，上空から見ると直角三角形になっています。この面積を最大化すれば良いですね。

まず定義域を考えておきましょう。 \(x\)は辺の長さですから，\(x > 0\)です。また，直角三角形は斜辺が一番長いので，\(x < 8\)です。まとめると\(0 < x < 8\)が定義域になります。

次は直角三角形の面積を\(y\)[\(\mathrm{m}^{2}\)]とし，\(x\)で表しましょう。底辺の長さが\(x\)なのは分かっていますから，あとは高さが分かれば面積を求められます。三平方の定理を使うと，高さが\(\sqrt{64 - x^2}\)であることが分かりますから，\(y\)は次のように表せます。

\( \begin{align} y = \displaystyle\frac{1}{2} x \sqrt{64 - x^2} \end{align} \)

見慣れない形の関数になりましたね。根号が厄介なので消してしまいたいです。そこで【注２】に注目です。これは「正の数は２乗しても大小関係は変わらないよ」という意味です。 \(y > 0\)ですから，２乗した\(y^2\)を考えてもいつ最大値をとるかが分かるわけです。（解答の最後で補足説明します。）

\(y^2\)は次のようになります。

\( \begin{align} y^2 &= \displaystyle\frac{1}{4} x^2 \left(64 - x^2 \right) \\[5pt] &= \displaystyle\frac{1}{4} \left(64x^2 - x^4 \right) \end{align} \)

よく見るとこれって２次関数に近い形になっていますね。 \(t = x^2\)とおくと，この関数は次のように変形できます。

\( \begin{align} y^2 = \displaystyle\frac{1}{4} \left(64t - t^2 \right) \end{align} \)

無事２次関数になりました！でもまだ油断しないでください。 \(t\)の定義域がまだ分かっていません。 \(t = x^2\)で\(x\)の定義域が\(0 < x < 8\)ですから，\(t\)の定義域は\(0 < t < 64\)ですね。

あとはいつ最大値をとるか考えるだけです。関数式を平方完成しましょう。

\( \begin{align} y^2 &= \displaystyle\frac{1}{4} \left(64t - t^2 \right) \\[5pt] &= -\displaystyle\frac{1}{4} (t^2 - 64t) \\[5pt] &= -\displaystyle\frac{1}{4} (t - 32)^2 + \displaystyle\frac{1}{4} \cdot 32^2 \end{align} \)

\(y^2\)のグラフは\(t = 32\)を軸とする上に凸の放物線ですね。 \(t\)の定義域は\(0 < t < 64\)で，軸が定義域に含まれていますから，グラフをかくまでもなく，この関数は\(t = 32\)のとき最大値をとります。

\(t = x^2\)でしたから，このとき\(x^2 = 32\)です。 \(x > 0\)ですから，\(x = 4\sqrt{2}\)と求められますね。

【注２】の活用について補足です。関数\(f(x)\)が\(x = a\)で最大値をとるとは，「定義域内のすべての\(x\)について，\(f(x) \leqq f(a)\)である」ということです。もし常に\(f(x) > 0\)であれば，【注２】を活用できて，これは「定義域内のすべての\(x\)について，\(f(x)^2 \leqq f(a)^2\)である」と同値です。

つまり，常に\(f(x) > 0\)であるとき，関数\(f(x)\)が\(x = a\)で最大値をとることと，関数\(f(x)^2\)が\(x = a\)で最大値をとることは同値なのです。

今回の問題では，常に\(y > 0\)ですから，最大値をとる\(x\)を考えるのに，代わりに\(y^2\)を使うことができたわけですね。