２次関数の決定

はじめに

今までは主に，与えられた２次関数について考えてきました。今回は，ある条件を満たす２次関数を見つける練習をします。

２次関数の表し方

▼

今回は，条件を満たす２次関数を見つける練習をします。そのために，まずは２次関数の表し方を確認しておきましょう。２次関数の表し方には，次の３つがあります。

２次関数の表し方

　一般形
$y = a x^{2} + b x + c$
　頂点が $(p, q)$
$y = a (x - p)^{2} + q$
　 $x$ 切片の $x$ 座標が $α, β$
$y = a (x - α) (x - β)$

色んな表し方がありますね。状況に応じて使いやすい形で表せば，計算が楽になります。次項から詳しく見ていきましょう。

一般形

▲

▼

まずは２次関数の一般的な表し方から確認します。２次関数は，２次式の関数ですから，以下の形で表せましたね。

\begin{array}{r} y = a x^{2} + b x + c \end{array}

具体的な式を求めるには， $a, b, c$ ３つの未知数を求める必要があります。関数のグラフが通る点が３つ分かっていれば，方程式が３つ得られ，３つの未知数が分かるようになります。

例えば，「グラフが３点 $(0, 3), (1, 6), (2, 11)$ を通る２次関数を求めよ」という問題を考えてみましょう。ひとまず２次関数を次のように表しておいて， $a, b, c$ を求めましょう。

\begin{array}{r} y = a x^{2} + b x + c \end{array}

このグラフが上記３点を通るわけですから， $x, y$ にそれぞれの点の座標を代入した式が成り立ちます。

\begin{array}{r} {\begin{cases} 3 & = a \cdot 0^{2} + b \cdot 0 + c \\ 6 & = a \cdot 1^{2} + b \cdot 1 + c \\ 11 & = a \cdot 2^{2} + b \cdot 2 + c \end{cases} \end{array}

式を整理すると，次のようになります。

\begin{array}{r} {\begin{cases} c & = 3 \\ a + b + c & = 6 \\ 4 a + 2 b + c & = 11 \end{cases} \end{array}

この連立方程式を解くと， $(a, b, c) = (1, 2, 3)$ と求められます。これで，この２次関数が次の式で表されることが分かりました。

\begin{array}{r} y = x^{2} + 2 x + 3 \end{array}

このように，２次関数のグラフが通る点が３つ分かっているときは，この表し方が便利です。

頂点が分かる場合

▲

▼

２次関数の式を平方完成すると，頂点の座標が一目で分かるようになりました。頂点の座標を $(p, q)$ とすると，２次関数は次のように表せます。

\begin{array}{r} y = a (x - p)^{2} + q \end{array}

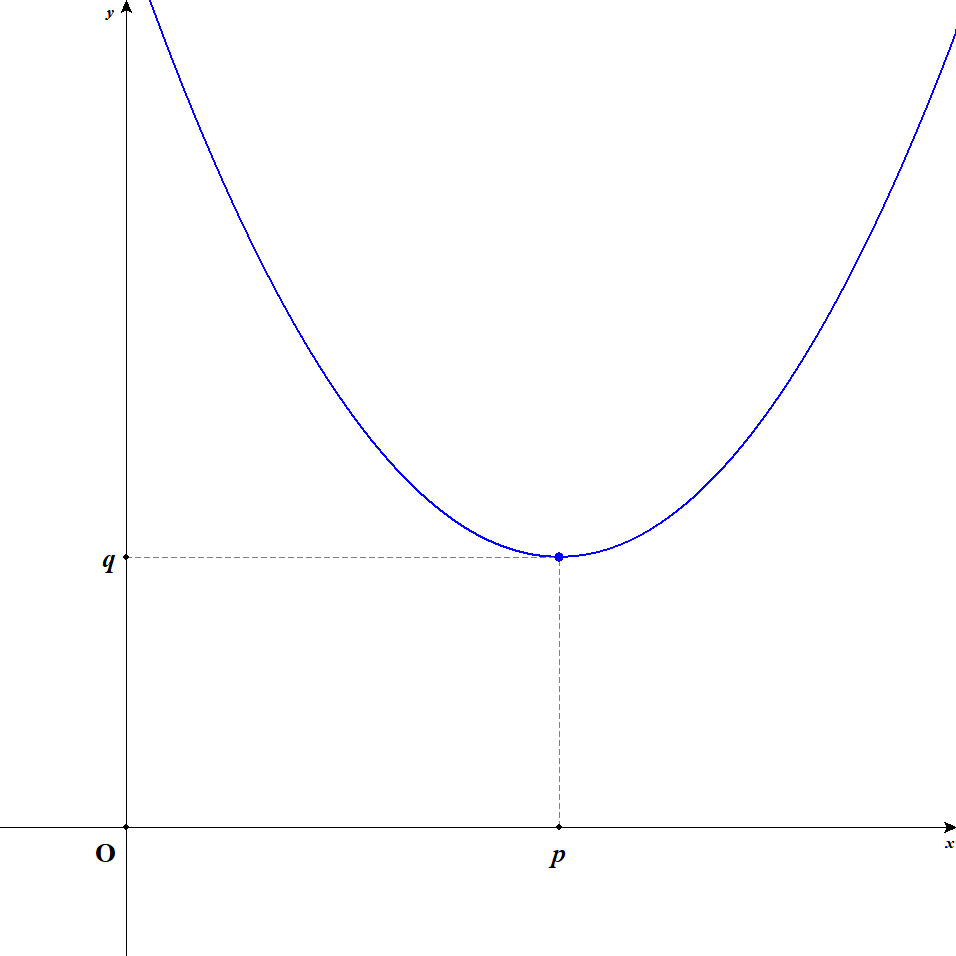
頂点が分かっているときには，未知数は $a$ ひとつだけですね。

例えば，「グラフの頂点が $(1, 1)$ であり，点 $(2, 5)$ を通る２次関数を求めよ」という問題を考えてみましょう。グラフの頂点が分かっているので，２次関数の式は次のように表せます。

\begin{array}{r} y = a (x - 1)^{2} + 1 \end{array}

このグラフが点 $(2, 5)$ を通るので，その座標を $x, y$ に代入すれば， $a$ を求められます。

\begin{array}{r} 5 = a (2 - 1)^{2} + 1 \end{array}

式を整理することで $a = 4$ と求められ，この２次関数が次の式で表されることが分かりました。

\begin{array}{r} y = 4 (x - 1)^{2} + 1 \end{array}

このように，２次関数のグラフの頂点が分かっているときは，この表し方が便利です。

$x$ 切片が分かる場合

▲

▼

最後に $x$ 切片を使った表し方を紹介します。 $x$ 切片は，２次関数のグラフが $x$ 軸とぶつかる点ですね。詳しくは次回以降で学びますが， $x$ 切片は０～２個あります。

まず $x$ 切片が２つある場合を考え，その $x$ 座標を $α, β$ としましょう。グラフが次のようになる場合です。

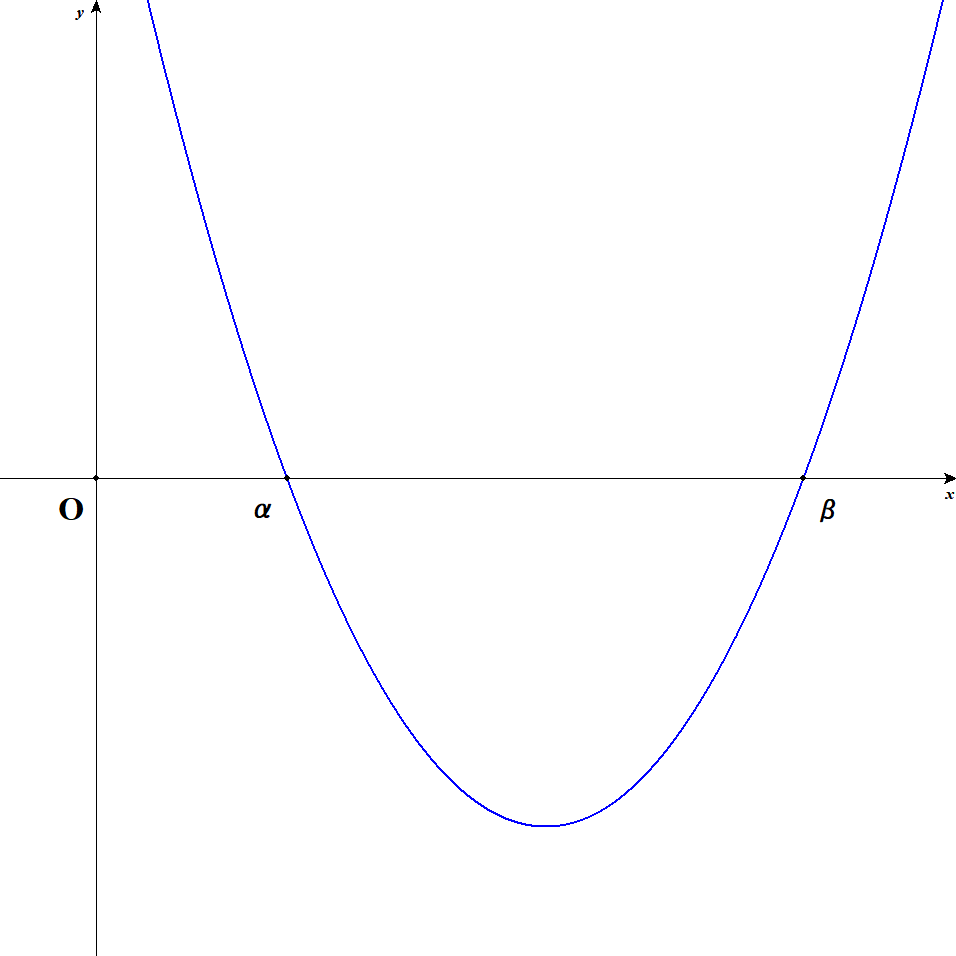
このとき，２次関数の式は次の形で表せます。

\begin{array}{r} y = a (x - α) (x - β) \end{array}

補足なぜこの形か

２次関数の $x$ 切片が $(α, 0), (β, 0)$ であるとき，関数の式が $y = a (x - α) (x - β)$ で表せる理由を考えましょう。ただし詳細を理解するには，次回以降で学ぶ２次方程式の知識が必要です。（さらに詳しくは，数学Ⅱで学ぶ因数定理が理解に役立ちます。）

２次関数の式は，一般には $y = a x^{2} + b x + c$ と表せました。 $x$ 切片は，この式で $y = 0$ となるときの $x$ の値ですから，次の２次方程式の解です。

\begin{array}{r} a x^{2} + b x + c = 0 \end{array}

$x$ 切片の $x$ 座標が $α, β$ であるということは，この左辺が次の式のように因数分解できるということです。

\begin{array}{r} a (x - α) (x - β) = 0 \end{array}

これで，２次関数の式も次のように因数分解できることが分かります。

\begin{aligned} y & = a x^{2} + b x + c \\ = a (x - α) (x - β) \end{aligned}

次に， $x$ 切片が１つだけの場合も考えましょう。 $x$ 切片の $x$ 座標を $α$ とします。グラフが次のようになる場合です。

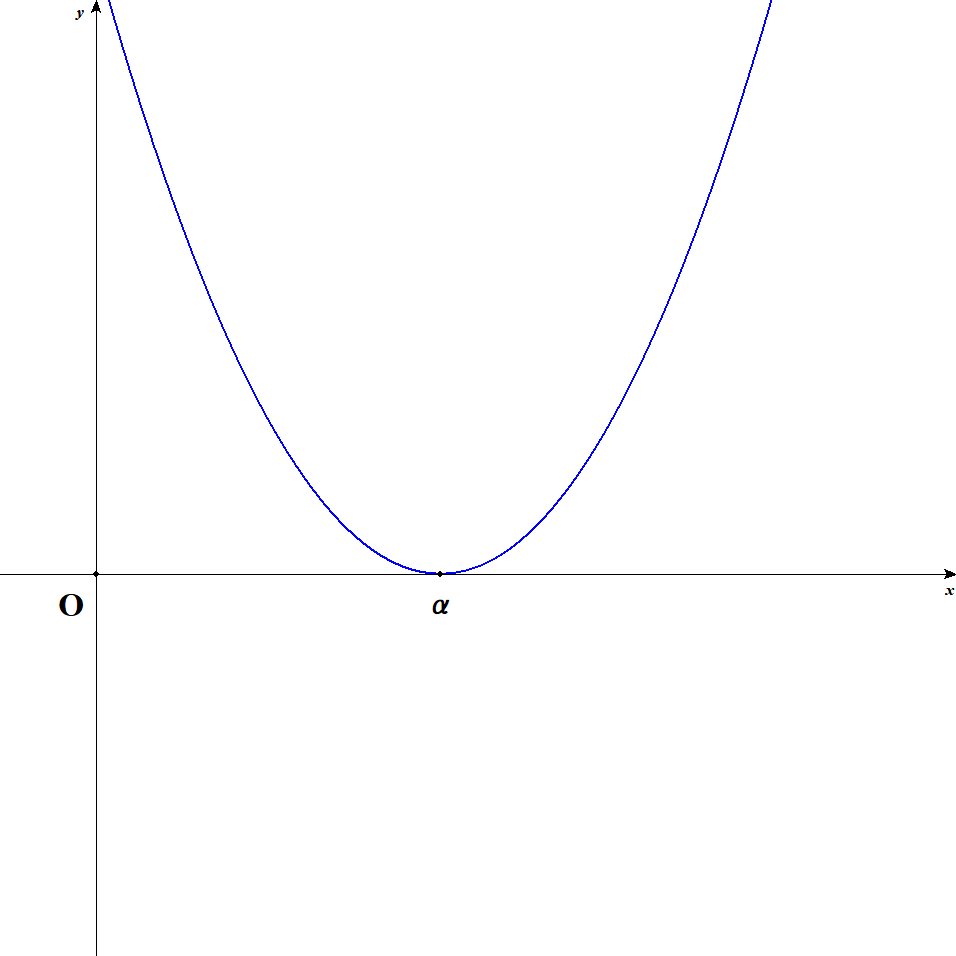
このとき，２次関数の式は次の形で表せます。さきほどの式で $β$ を $α$ に変えたのと同じ形ですね。

\begin{array}{r} y = a (x - α)^{2} \end{array}

$x$ 切片が１個でも２個でも， $x$ 切片が分かっているときには，未知数は $a$ ひとつだけですね。

例えば，「グラフの $x$ 切片が $(- 1, 0), (1, 0)$ であり，点 $(2, 3)$ を通る２次関数を求めよ」という問題を考えてみましょう。 $x$ 切片が分かっているので，２次関数の式は次のように表せます。

\begin{array}{r} y = a (x - 1) (x + 1) \end{array}

このグラフが点 $(2, 3)$ を通るので，その座標を $x, y$ に代入すれば， $a$ を求められます。

\begin{array}{r} 3 = a (2 - 1) (2 + 1) \end{array}

式を整理することで $a = 1$ と求められ，この２次関数が次の式で表されることが分かりました。

\begin{array}{r} y = (x - 1) (x + 1) \end{array}

このように， $x$ 切片が分かっているときには，この表し方が便利です。

確認問題

▲

グラフが次の条件を満たす２次関数をそれぞれ求めてください。

３点 $(1, 2), (2, 1), (3, - 2)$ を通る
$(2, - 3)$ を頂点とし，点 $(4, 5)$ を通る
$x$ 切片を $(- 1, 0), (- 3, 0)$ とし，点 $(- 4, - 6)$ を通る

答え

与えられた条件に応じて，計算が楽になるように２次関数の表し方を考えましょう。

３点を通ることだけが分かっていて，頂点や切片は分かりません。この場合は，２次関数を次のように一般形で表すことにしましょう。

$\begin{array}{r} y = a x^{2} + b x + c \end{array}$

このグラフが３点 $(1, 2), (2, 1), (3, - 2)$ を通ることから，次の連立方程式が得られます。

$\begin{array}{r} {\begin{cases} 2 = a \cdot 1^{2} + b \cdot 1 + c \\ 1 = a \cdot 2^{2} + b \cdot 2 + c \\ - 2 = a \cdot 3^{2} + b \cdot 3 + c \end{cases} \end{array}$

整理すると，次のようになります。

$\begin{array}{r} {\begin{cases} a + b + c & = 2 \\ 4 a + 2 b + c & = 1 \\ 9 a + 3 b + c & = - 2 \end{cases} \end{array}$

これを解くと， $(a, b, c) = (- 1, 2, 1)$ です。したがって，題意の２次関数は $y = - x^{2} + 2 x + 1$ です。
頂点が $(2, - 3)$ だと分かっているので，題意の２次関数は次のように表せます。

$\begin{array}{r} y = a (x - 2)^{2} - 3 \end{array}$

このグラフが点 $(4, 5)$ を通ることから，次の方程式が得られます。

$\begin{array}{r} 5 = a (4 - 2)^{2} - 3 \end{array}$

これを整理して解くと， $a = 2$ です。したがって，題意の２次関数は $y = 2 (x - 2)^{2} - 3$ です。
$x$ 切片が $(- 1, 0), (- 3, 0)$ だと分かっているので，題意の２次関数は次のように表せます。

$\begin{array}{r} y = a (x + 1) (x + 3) \end{array}$

このグラフが点 $(- 4, - 6)$ を通ることから，次の方程式が得られます。

$\begin{array}{r} - 6 = a (- 4 + 1) (- 4 + 3) \end{array}$

これを整理して解くと， $a = - 2$ です。したがって，題意の２次関数は $y = - 2 (x + 1) (x + 3)$ です。

グラフが次の条件を満たす２次関数をそれぞれ求めてください。

$y = 2 x^{2}$ のグラフを平行移動したもので，２点 $(- 1, - 6), (2, 9)$ を通る
$y = - 3 x^{2} + 4 x + 2$ のグラフを平行移動したもので，２点 $(- 2, 0), (5, 0)$ を通る

答え

２次関数のグラフの形は， $x^{2}$ の係数によって決まります。グラフを平行移動しても，グラフの位置が変わるだけで，形は変わらないことに注意すると，平行移動しても $x^{2}$ の係数は変わらないことが分かります。このことを利用すると，計算が簡単に行えます。

頂点や切片の情報が与えられていないので，関数の式は一般形で表すことにしましょう。ただし，グラフの形は平行移動前と変わらないので， $x^{2}$ の係数は引き継ぎます。このことを踏まえると，関数は次のように表せます。

$\begin{array}{r} y = 2 x^{2} + b x + c \end{array}$

このグラフが２点 $(- 1, - 6), (2, 9)$ を通ることから，次の連立方程式が得られます。

$\begin{array}{r} {\begin{cases} - 6 & = 2 \cdot (- 1)^{2} + b \cdot (- 1) + c \\ 9 & = 2 \cdot 2^{2} + b \cdot 2 + c \end{cases} \end{array}$

整理すると，次のようになります。

$\begin{array}{r} {\begin{cases} - b + c & = - 8 \\ 2 b + c & = 1 \end{cases} \end{array}$

これを解くと， $(b, c) = (3, - 5)$ です。したがって，題意の２次関数は $y = 2 x^{2} + 3 x - 5$ です。
平行移動前のグラフの方程式が分かっているので， $x^{2}$ の係数は $- 3$ です。また， $x$ 切片が $(- 2, 0), (5, 0)$ ですから，題意の２次関数は次のように表せます。

$\begin{array}{r} y = - 3 (x + 2) (x - 5) \end{array}$