２次方程式の解法

はじめに

２次関数は２次式の関数ですから，２次関数についていろいろ調べていると，２次式の方程式が現れることもあります。それを２次方程式といいますが，今回はその解法を解説します。

因数分解による解法

▼

２次方程式は２次式の方程式です。中学でも習いましたね。基本的な解法は，因数分解によるものです。次の２次方程式を解いてみましょう。

\( \begin{align} 2x^2 + 7x + 6 = 0 \end{align} \)

これを解くには，まず左辺を因数分解します。

\( \begin{align} (x + 2)(2x + 3) = 0 \end{align} \)

因数分解すると左辺が積の形になります。積が\(0\)になるのは，かけた数の中に\(0\)がある場合だけですから，この式が成り立つのは，次の式のいずれかが成り立つ場合のみです。

\( \begin{align} x + 2 &= 0 \\[5pt] 2x + 3 &= 0 \end{align} \)

それぞれの方程式を解くことで，この２次方程式の解が\(x = -2, -\displaystyle\frac{3}{2}\)であることが分かります。このコンマは「または」の意味です。 \(x\)がこのどちらかの場合のみ，方程式が成り立つということです。

このように，整式の形をした方程式を解くときは，「整式\(= 0\)」の形にして因数分解するのが基本です。

因数分解すると左辺が積の形になります。積が\(0\)ということは，かけた数，つまり因数のどれかが\(0\)ということです。「因数\(= 0\)」という方程式に分解できるわけですね。

２次方程式であれば，因数分解すれば２つの１次方程式に分解できるので，簡単に解けるわけです。

解の公式

▲

▼

２次方程式を解くときには因数分解するのが基本ですが，因数分解って難しいですよね。そもそも有理数の範囲では因数分解できない２次式もあります。

これでは不便なので，一般に使える公式を作りましょう。次の２次方程式を解きます。

\( \begin{align} ax^2 + bx + c = 0 \end{align} \)

２次方程式なので\(a \neq 0\)です。結論を先にいうと，公式は次のようになります。計算はその後で確認していきます。

２次方程式の解の公式

２次方程式\(ax^2 + bx + c = 0\)は，\(b^2 - 4ac \geqq 0\)のとき実数解をもち，その解は次の通り：

\( \begin{align} x = \displaystyle\frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \end{align} \)

ただし，\(b^2 - 4ac < 0\)の場合は「実数解なし」となる。

それでは，２次方程式\(ax^2 + bx + c = 0\)を解いていきましょう。まずは最高次である\(x^2\)の係数を簡単にするため，両辺を\(a\)で割ります。２次方程式なので，\(a \neq 0\)ですから，両辺を\(a\)で割ることができるんですね。

\( \begin{align} x^2 + \displaystyle\frac{b}{a}x + \displaystyle\frac{c}{a} = 0 \end{align} \)

次に，\(x\)を含む項が\(x^2, x\)の２つあって面倒なので，左辺を平方完成します。

\( \begin{align} \left(x + \displaystyle\frac{b}{2a}\right)^2 - \left(\displaystyle\frac{b}{2a}\right)^2 + \displaystyle\frac{c}{a} &= 0 \\[5pt] \left(x + \displaystyle\frac{b}{2a}\right)^2 - \displaystyle\frac{b^2}{4a^2} + \displaystyle\frac{4ac}{4a^2} &= 0 \\[5pt] \left(x + \displaystyle\frac{b}{2a}\right)^2 - \displaystyle\frac{b^2 - 4ac}{4a^2} &= 0 \end{align} \)

次に，左辺が\(x\)を含む項だけ，右辺が\(x\)を含まない項だけになるように分離します。

\( \begin{align} \left(x + \displaystyle\frac{b}{2a}\right)^2 = \displaystyle\frac{b^2 - 4ac}{4a^2} \end{align} \)

この方程式の左辺は\(0\)以上なので，右辺が\(0\)以上のときにしか実数解はありません。右辺の分母は正ですから，右辺が\(0\)以上になるのは\(b^2 - 4ac \geqq 0\)のときですね。

このとき，左辺の２乗をはずすことができます。２乗するとある数になるものを平方根といい，\(\sqrt{\quad}\)をつけて表すんでしたね。

\( \begin{align} x + \displaystyle\frac{b}{2a} &= \pm \sqrt{\displaystyle\frac{b^2 - 4ac}{4a^2}} \\[5pt] &= \pm \displaystyle\frac{\sqrt{b^2 - 4ac}}{\sqrt{4a^2}} \\[5pt] &= \pm \displaystyle\frac{\sqrt{b^2 - 4ac}}{2|a|} \\[5pt] &= \pm \displaystyle\frac{\sqrt{b^2 - 4ac}}{2a} \end{align} \)

補足絶対値とプラスマイナス

上の式変形では\(\sqrt{a^2} = |a|\)を利用していますが，次の行では絶対値が消えています。それは，絶対値記号の前に符号\(\pm\)があるからです。

\(|a|\)の絶対値を外すと，\(a\)または\(-a\)になります。なので\(\pm |a|\)は，\(\pm a\)または\(\mp a\)になります。しかし，今回のように符号の順番に意味がない場合は，\(\pm a\)も\(\mp a\)も同じ組み合わせであり，両者に違いはありません。

したがって，\(\pm |a| = \pm a\)と変形できたわけです。

あとは左辺の定数項をどかして終わりですね。

\( \begin{align} x &= -\displaystyle\frac{b}{2a} \pm \displaystyle\frac{\sqrt{b^2 - 4ac}}{2a} \\[5pt] &= \displaystyle\frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \end{align} \)

ちゃんと公式が求められましたね。

補足派生型

解の公式には，よく使われる次の派生型があります。 \(x\)の係数が偶数の場合の公式です。

２次方程式が\(ax^2 + \textcolor{red}{2b'}x + c = 0\)という形をしているとき，解の公式は次の形になります。

\( \begin{align} x = \displaystyle\frac{-\textcolor{red}{b'} \pm \sqrt{\textcolor{red}{b'}^2 - ac}}{a} \end{align} \)

\(x\)の係数が偶数の場合は，普通に解の公式を使うと，約分箇所が出てきます。それをあらかじめ考慮した公式ですね。 \(x\)の係数を\(2b'\)としているので，公式中では\(x\)の係数の半分を使っていることになります。

この公式を覚える必要はありませんが，使いこなすと計算が楽になります。たまには意識して使ってみると良いかもしれません。

補足解の公式のパーツ

解の公式には\(-\displaystyle\frac{b}{2a}\)と\(\displaystyle\frac{\sqrt{b^2 - 4ac}}{2a}\)というパーツが登場します。これは，関数\(y = ax^2 + bx + c\)のグラフを考えると，前者は軸で，後者は軸から\(x\)切片までの距離です。

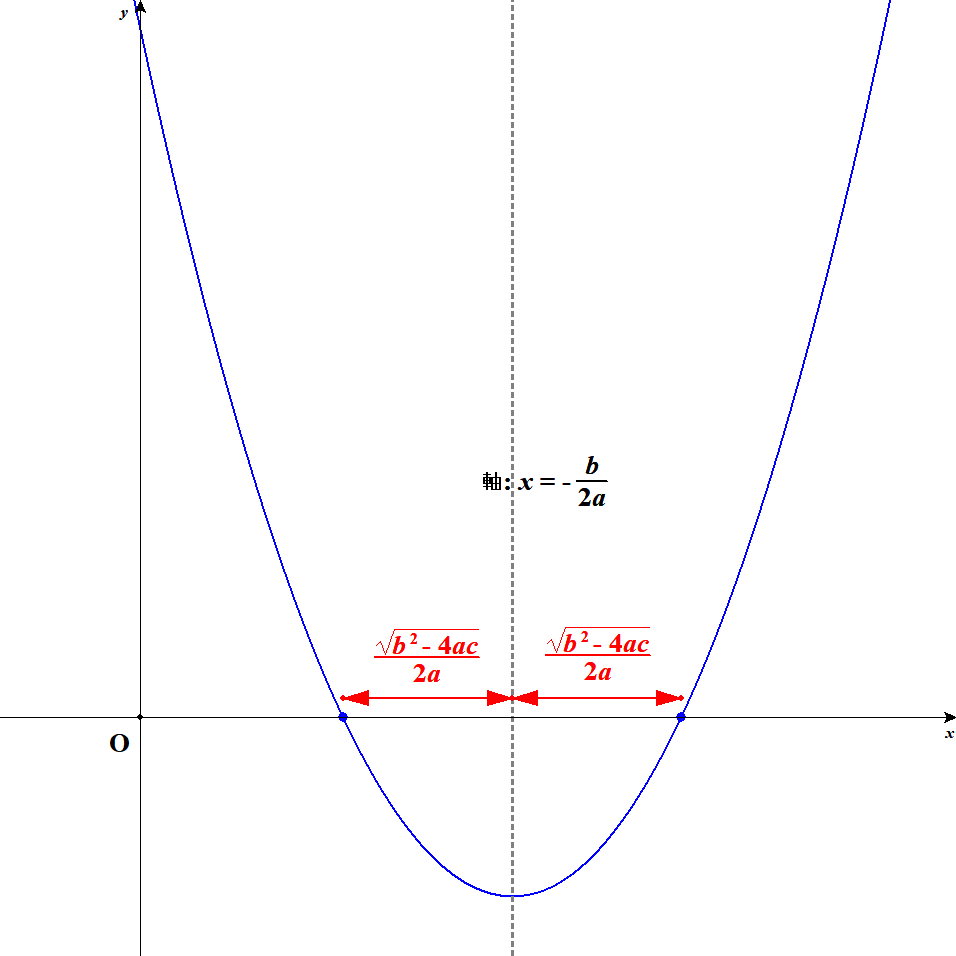
２次関数のグラフ，つまり放物線は，軸を対称軸として左右対称です。ですから，軸から\(x\)切片までの距離は，左側でも右側でも変わりません。

２次方程式の解の公式は，２次関数の値が\(0\)になるような\(x\)の値，つまり\(x\)切片を求める公式でもあるので，「"軸の座標" \(\pm\) "\(x\)切片までの距離"」という形をしているわけです。

確認問題

▲

次の方程式を解いてください。

\(x^2 = 4x - 3\)
\(x(6x - 5) = -1\)
\(x^2 + x + 2 = 3\)
\((x + 1)^2 + x(x + 2) = 0\)

答え

まずは方程式を「整式\(= 0\)」の形に整理し，因数分解か解の公式で解きましょう。

方程式を整理すると，次のようになります。

\( \begin{align} x^2 - 4x + 3 = 0 \end{align} \)

左辺を因数分解すると，次のようになります。

\( \begin{align} (x - 1)(x - 3) = 0 \end{align} \)

積が\(0\)ということは，因数のどちらかは\(0\)です。なので，「因数\(= 0\)」を解くことで方程式の解が求められ，その解は\(x = 1, 3\)です。

解の公式を使った場合は，次のようになります。 \(x\)の係数が偶数なので，派生型の方を使ってみます。

\( \begin{align} x &= \displaystyle\frac{2 \pm \sqrt{2^2 - 1 \cdot 3}}{1} \\[5pt] &= 2 \pm \sqrt{1} \\[5pt] &= 2 \pm 1 \\[5pt] &= 2 + 1, 2 - 1 \\[5pt] &= \textcolor{red}{3, 1} \end{align} \)
方程式を整理すると，次のようになります。

\( \begin{align} 6x^2 - 5x &= -1 \\[5pt] 6x^2 - 5x + 1 &= 0 \end{align} \)

左辺を因数分解すると，次のようになります。

\( \begin{align} (2x - 1)(3x - 1) = 0 \end{align} \)

積が\(0\)ということは，因数のどちらかは\(0\)です。なので，「因数\(= 0\)」を解くことで方程式の解が求められ，その解は\(x = \displaystyle\frac{1}{2}, \displaystyle\frac{1}{3}\)です。

解の公式を使った場合は，次のようになります。

\( \begin{align} x &= \displaystyle\frac{-(-5) \pm \sqrt{(-5)^2 - 4 \cdot 6 \cdot 1}}{2 \cdot 6} \\[5pt] &= \displaystyle\frac{5 \pm \sqrt{1}}{12} \\[5pt] &= \displaystyle\frac{5 \pm 1}{12} \\[5pt] &= \displaystyle\frac{5 + 1}{12}, \displaystyle\frac{5 - 1}{12} \\[5pt] &= \textcolor{red}{\displaystyle\frac{1}{2}, \displaystyle\frac{1}{3}} \end{align} \)
方程式を整理すると，次のようになります。

\( \begin{align} x^2 + x - 1 = 0 \end{align} \)

左辺の因数分解が難しそうなので，解の公式を使います。

\( \begin{align} x &= \displaystyle\frac{-1 \pm \sqrt{1^2 - 4 \cdot 1 \cdot (-1)}}{2 \cdot 1} \\[5pt] &= \textcolor{red}{\displaystyle\frac{-1 \pm \sqrt{5}}{2}} \end{align} \)

ちなみに，解が求められたことで，左辺が次のように因数分解できることが分かります。

\( \begin{align} \left(x - \displaystyle\frac{-1 + \sqrt{5}}{2}\right)\left(x - \displaystyle\frac{-1 - \sqrt{5}}{2}\right) \end{align} \)
方程式を整理すると，次のようになります。

\( \begin{align} x^2 + 2x + 1 + x^2 + 2x &= 0 \\[5pt] 2x^2 + 4x + 1 &= 0 \end{align} \)

左辺の因数分解が難しそうなので，解の公式を使います。 \(x\)の係数が偶数なので，派生型の方を使ってみます。

\( \begin{align} x &= \displaystyle\frac{-2 \pm \sqrt{2^2 - 2 \cdot 1}}{2} \\[5pt] &= \textcolor{red}{\displaystyle\frac{-2 \pm \sqrt{2}}{2}} \end{align} \)

ちなみに，解が求められたことで，左辺が次のように因数分解できることが分かります。

\( \begin{align} \left(x - \displaystyle\frac{-2 + \sqrt{2}}{2}\right)\left(x - \displaystyle\frac{-2 - \sqrt{2}}{2}\right) \end{align} \)

次の方程式を解いてください。

\(\displaystyle\frac{3x}{x^2 + 1} = 1\)
\(|x|^2 + |x| - 2 = 0\)

答え

式を整理して「整式\(= 0\)」の形をつくることから始めます。式変形の際には，それが同値変形になっているか，つまり，式変形を逆方向にたどれるかに注意が必要です。

例えば，\(x + 1 = 2\)という方程式を考えるとき，式変形として両辺に\(0\)を掛けてみましょう。このとき，方程式は\(0 = 0\)になり，\(x\)の値に関わらず式が成り立つようになります。したがって，この方程式の解はすべての実数である・・・とは，当然できません。

この式変形の問題点は，逆にたどれないことです。式変形として両辺に\(0\)を掛けたので，逆の計算とは両辺を\(0\)で割ることですが，それは「\(0\)割り禁止」というルールに反するため不可能なのです。

逆にたどって元の式に戻れないということは，もはや元の式とは別物であるということです。方程式の変形の際，特に両辺に何か式を掛ける場合などは，十分に気を付けましょう。

方程式が分数の形になっているので，両辺に分母と同じ式を掛けて，分母を払いましょう。

\( \begin{align} 3x = x^2 + 1 \end{align} \)

ここで，式変形を逆方向にたどれることが重要です。逆方向の計算とは，両辺を\(x^2 + 1\)で割ることですが，\(x^2 + 1\)は常に正であり，\(0\)にならないので，それが可能なのです。

引き続き，式を整理していきます。

\( \begin{align} x^2 - 3x + 1 = 0 \end{align} \)

これで見慣れた２次方程式になりました。左辺の因数分解は難しそうなので，解の公式を使って解を求めてしまいましょう。

\( \begin{align} x &= \displaystyle\frac{-(-3) \pm \sqrt{(-3)^2 - 4 \cdot 1 \cdot 1}}{2 \cdot 1} \\[5pt] &= \textcolor{red}{\displaystyle\frac{3 \pm \sqrt{5}}{2}} \end{align} \)
方程式に絶対値があるので，場合分けして絶対値を外しましょう。 \(x \geqq 0\)のとき\(|x| = x\)，\(x < 0\)のとき\(|x| = -x\)ですね。

[1] \(x \geqq 0\)の場合：
方程式は次のようになります。

\( \begin{align} x^2 + x - 2 = 0 \end{align} \)

左辺を因数分解すると，次のようになります。

\( \begin{align} (x + 2)(x - 1) = 0 \end{align} \)

これを解くと\(x = -2, 1\)ですが，いま考えているのは\(x \geqq 0\)の場合です。この条件に当てはまる解は\(x = 1\)だけですね。

[2] \(x < 0\)の場合：
方程式は次のようになります。

\( \begin{align} x^2 - x - 2 = 0 \end{align} \)

左辺を因数分解すると，次のようになります。

\( \begin{align} (x + 1)(x - 2) = 0 \end{align} \)

これを解くと\(x = -1, 2\)ですが，いま考えているのは\(x < 0\)の場合です。この条件に当てはまる解は\(x = -1\)だけですね。

以上から，この方程式の解は\(x = -1, 1\)です。

足すと\(50\)，掛けると\(100\)になる２つの数は何でしょうか？

答え

求める２つの数を\(x, y\)とおきましょう。そうすると，この問題は次の連立方程式で表せます。

\( \begin{eqnarray} \left\{ \begin{array}{l} x + y &= 50 \\ xy &= 100 \end{array} \right. \end{eqnarray} \)

見慣れない形の連立方程式かもしれませんが，「文字を減らす」という方針はいつでも変わりません。いわゆる加減法は使えそうにないので，代入法を使います。

１つめの式は\(y = 50 - x\)と変形できますから，これを２つめの式に代入しましょう。

\( \begin{align} x(50 - x) &= 100 \\[5pt] 50x - x^2 &= 100 \\[5pt] x^2 - 50x + 100 &= 0 \end{align} \)

左辺を因数分解するのは難しそうなので，解の公式で\(x\)を求めます。 \(x\)の係数が偶数なので，派生型の方を使います。

\( \begin{align} x &= \displaystyle\frac{-(-25) \pm \sqrt{(-25)^2 - 1 \cdot 100}}{1} \\[5pt] &= 25 \pm \sqrt{25^2 - 4 \cdot 25} \\[5pt] &= 25 \pm \sqrt{25(25 - 4)} \\[5pt] &= 25 \pm 5\sqrt{21} \end{align} \)

\(x = 25 + 5\sqrt{21}\)のときは，\(y\)は次のように求められます。

\( \begin{align} y &= 50 - x \\[5pt] &= 50 - 25 - 5\sqrt{21} \\[5pt] &= 25 - 5\sqrt{21} \end{align} \)

\(x = 25 - 5\sqrt{21}\)のときは，\(y\)は次のように求められます。

\( \begin{align} y &= 50 - x \\[5pt] &= 50 - 25 + 5\sqrt{21} \\[5pt] &= 25 + 5\sqrt{21} \end{align} \)

これで２つの数の組み合わせとして，\(25 + 5\sqrt{21}, \ 25 - 5\sqrt{21}\)と\(25 - 5\sqrt{21}, \ 25 + 5\sqrt{21}\)が得られました。

しかし，よく見ると両者は同じ組み合わせです。式の上では\(x\)と\(y\)は区別されてきたので，\(x, y\)の入れ替わった２つの解が得られたのです。実際には\(x, y\)の区別に意味はないので，得られた２つの解は全く同じ組み合わせになったのです。

以上から，求める２つの数は\(25 + 5\sqrt{21}, \ 25 - 5\sqrt{21}\)です。

ちなみに，最後の\(y\)を求める計算は，次のようにまとめてもＯＫです。

\( \begin{align} y &= 50 - x \\[5pt] &= 50 - (25 \pm 5\sqrt{21}) \\[5pt] &= 50 - 25 \mp 5\sqrt{21} \\[5pt] &= 25 \mp 5\sqrt{21} \\[5pt] \end{align} \)