今回は特定の解をもつ2次方程式などを考えます。 現実問題に当てはめると,特定の性質をもつ2次関数を考えることは,今ある関数の結果をただ受け入れるのではなく,理想の関数に改良していくことに繋がります。
目次
解の条件
2次関数\(f(x) = ax^2 + bx + c\)に対して,2次方程式\(f(x) = 0\)の解に条件が与えられている状況を考えましょう。 判別式を\(D = b^2 - 4ac\),2つの実数解を\(\alpha, \beta \ (\alpha \leqq \beta)\)としておきます。
どんな\(f(x)\)が解の条件を満たすかを調べるには,解の条件を\(a, b, c\)に関する必要十分条件として表すことができれば良いですね。 そのような条件を見つけるには,「\(f(x)\)のグラフがどうなるべきか」に注目することが重要です。
いくつかのケースについて考えてみましょう。
Case 1: 解の個数の条件
まずは簡単な問題から。 今まで何度も見てきたように,2次方程式の実数解の個数は,判別式\(D\)の符号を見れば分かります。
| 判別式の符号 | 実数解の個数 |
|---|---|
| \(D > 0\) | \(2\)個 |
| \(D = 0\) | \(1\)個 |
| \(D < 0\) | \(0\)個 |
なぜこれで実数解の個数が分かるのか忘れた人は,2次方程式の解の公式を思い出してください。 解の公式は次の通りです。
\(D < 0\)だと\(\sqrt{\quad}\)の中身がマイナスになってしまい,そんな実数は存在しないから実数解の個数は\(0\)です。 \(D > 0\)のときは実数解が\(\pm\)の\(2\)個あり,\(D = 0\)のときは\(\pm\)の区別がなくなるので,実数解が\(1\)個になるわけですね。
Case 2: 解の符号の条件
次は解の符号に条件がある場合を考えましょう。 例として,異なる2解が両方とも正の場合を考えます。 また,放物線は下に凸(\(a > 0\))としておきます。
まず実数解が2個あることから,判別式について次の条件が必要ですね。
しかしこの条件だけでは,十分ではありません。 まだ実数解が2個であると決まっただけで,その符号については何も触れられていないからです。
ここで少しグラフを考えてみましょう。 解が両方とも正であるとき,\(f(x)\)のグラフは次のようになります。
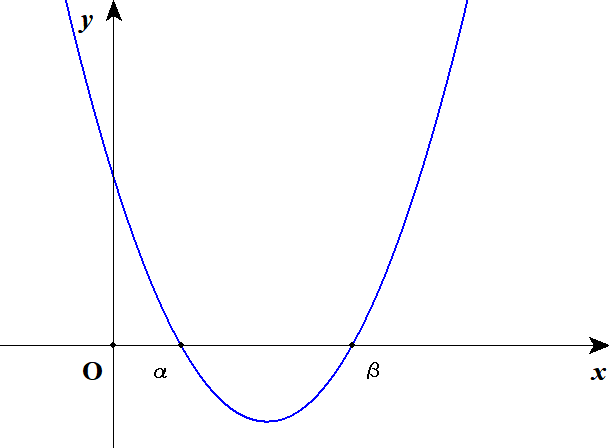
グラフを眺めてみると,解が両方とも正であるためには,グラフが\(y\)軸より右の方にないとダメみたいですね。 このことを条件に落とし込んでみましょう。
「グラフが右の方にある」を条件にしたいわけですから,グラフの位置に関する情報を使います。 グラフの左右の位置は「軸」で決まりますから,軸について次の条件が必要ですね。
以後,「軸の\(x\)座標\(> 0\)」を簡単に「軸\(> 0\)」ということにします。 さて,これで\(D > 0\)とあわせて2つの必要条件ができましたが,実はまだ十分ではありません。 例えば次のグラフは,作った2つの条件を満たしますが,解の条件を満たしません。
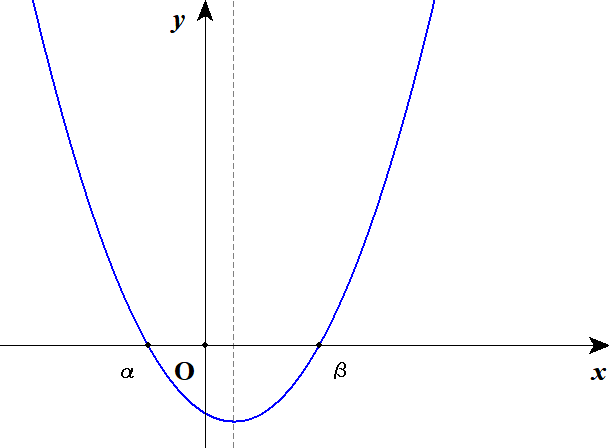
まだ条件が足りないようなので,もう少しよく考えてみましょう。
グラフの軸を\(y\)軸より右側に持ってきたので,少なくとも\(\beta\)は正になっているでしょう。 あとは\(\alpha\)が問題ですね。 \(\alpha\)が正のときのグラフをよく観察してみましょう。
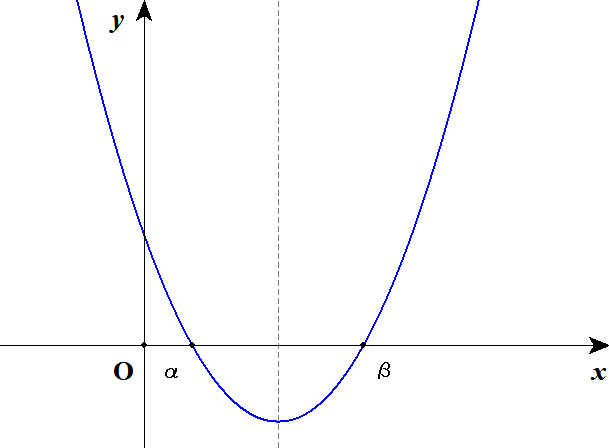
どうしたらグラフがこうなってくれるか・・・グラフを眺めていると,あることに気が付きます。 \(f(x)\)の符号は,\(\alpha\)の前後で変化するのです。
グラフは下に凸ですから,\(\alpha\)の位置で\(x\)軸をまたぐと\(f(x)\)の符号は正から負に変わります。 ということは,もし\(f(0)\)が負なら,グラフは\(y\)軸より左で既に\(x\)軸をまたいだということになり,\(\alpha\)が負になってしまいます。
つまり\(\alpha\)が正であるためには,次の条件が必要なんですね。
これで条件が3つ揃いました。 まず実数解が2つであるための条件,次に右側の解が正であるための条件,最後に左側の解も正であるための条件ですね。
この3条件はすべて不可欠です。 1つでも条件を欠くと,解が両方とも正にはならない場合が見つかりますから,条件を欠いた場合についても考えてみてください。
解の符号の条件については,他にも「解が両方とも負」や「解が正と負1つずつ」もあります。 これらについても必要十分条件を考えてみると,次の結果が得られます。
| 2解の条件 | 必要十分条件 | ||
|---|---|---|---|
| 判別式 | 軸 | \(f(0)\) | |
| 正と正 | \(D > 0\) | 軸\(> 0\) | \(f(0) > 0\) |
| 負と負 | \(D > 0\) | 軸\( < 0\) | \(f(0) > 0\) |
| 正と負 | 不要 | 不要 | \(f(0) < 0\) |
2つの実数解が負と負の場合については,正と正の場合とよく似ています。 軸が左側,つまり軸\(< 0\)であることが違いですね。 軸の条件から\(\alpha < 0\)となり,そこに\(f(0) > 0\)という条件を付け足すことで\(\beta < 0\)にもなるわけですね。
2つの実数解が正と負の場合については,判別式と軸についての条件は不要で,\(f(0) < 0\)だけで必要十分になります。 下図の通り,このときグラフは\(y\)軸の右側と左側で1回ずつ\(x\)軸をまたぐしかないのです。

解の符号の条件とは,解と\(0\)との大小関係の条件ですが,同じ考え方で一般の定数\(a\)について,解と\(a\)との大小関係の条件にも応用できます。 確認問題にもしておきますので,考えてみましょう。
Case 3: 解の範囲の条件
次は解が存在する範囲についての条件を考えてみましょう。 必要十分条件まで考えると厄介なので,十分条件だけ考えます。 まず\(a < x < b\)の範囲に解が存在するための十分条件を考えてみます。
前項で,グラフが\(x\)軸をまたぐときに\(f(x)\)の符号が変わることに注目しました。 逆に\(f(x)\)の符号がある2地点で異なるとき,その間で\(f(x)\)は\(x\)軸をまたぐことになります。
つまり\(f(a)\)と\(f(b)\)の符号が異なれば,\(f(x)\)は\(a < x < b\)の範囲に解を持つことになるのです。 \(f(a)\)と\(f(b)\)の符号が異なることは,\(f(a)f(b) < 0\)と表すことが出来ますから,次の十分条件が得られます。
つまりこの条件を満たすとき,\(f(x)\)は\(a < x < b\)の範囲に解を持つといえるわけです。
上の話は,2次関数については成り立ちますが,あらゆる関数について成り立つわけではありません。 詳しくは数学Ⅲで学びますが,グラフが「連続」であることが必要です。
連続とは,グラフが繋がっているということです。 \(f(x)\)が連続であるとき,\(f(a)\)と\(f(b)\)の符号が異なっていれば,当然\(a\)と\(b\)の間で\(x\)軸をまたぐことになるわけです。 もし連続という条件が抜けていれば,グラフが途切れて\(x\)軸をまたがない可能性があります。
\(f(a)f(b) < 0\)は\(a < x < b\)の範囲に解を持つための十分条件ですが,必要条件ではないので,使いどころには注意しましょう。
例えば次のグラフは,\(a < x < b\)の範囲に解を持っていますが,\(f(a)f(b) < 0\)ではありません。
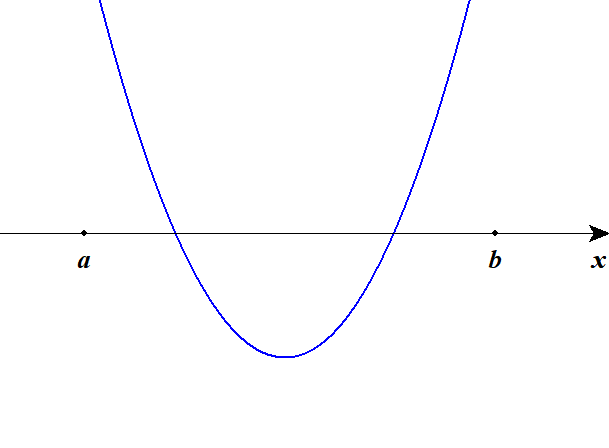
2回\(x\)軸をまたぐことで\(f(x)\)の符号が元に戻ったわけですね。 確認問題には,このように2次関数\(f(x)\)が\(a < x < b\)の範囲に実数解を2つ持つ条件を求める問題もあります。 挑戦してみてください。
確認問題
次の2次関数\(f(x)\)について,2次方程式\(f(x) = 0\)が正の実数解と負の実数解を1つずつ持つとき,定数\(a\)の値の範囲がどうなるか答えてください。
答え
\(f(x)\)のグラフは下に凸の放物線です。 その形状を思い浮かべれば,正と負の実数解を持つことは,\(f(0) < 0\)であることと同値だと分かります。 この不等式を解きましょう。
以上から,答えは\(a < \displaystyle\frac{1}{4}\)です。
次の2次関数\(f(x)\)について,2次方程式\(f(x) = 0\)が\(x < 2\)の範囲に異なる2つの実数解を持つとき,定数\(a\)の値の範囲がどうなるか答えてください。
答え
本文の議論を思い出して,問題の条件を具体的な式で表しましょう。 まず異なる2つの実数解を持つことから,判別式\(D\)は正です。 また放物線の軸の位置は\(x = 2\)よりも左側にある必要があります。 あとは\(f(2) > 0\)であればOKです。
あらかじめ判別式と軸を計算しておきましょう。 判別式は次の通りです。
軸は,次の平方完成の通り\(x = 2a\)です。
まず判別式の条件から,次の不等式を解く必要があります。
次に軸の条件から,次の不等式を解く必要があります。
そして最後の条件が\(f(2) > 0\)ですね。
以上で求めた3つの範囲の共通部分をとることで,題意を満たす\(a\)の範囲が次のようになることが分かります。
次の2次関数\(f(x)\)について,2次方程式\(f(x) = 0\)が\(-1 < x < 0\)の範囲と\(0 < x < 2\)の範囲に実数解を1つずつ持つとき,定数\(a\)の値の範囲がどうなるか答えてください。
答え
グラフの形を考えてみましょう。
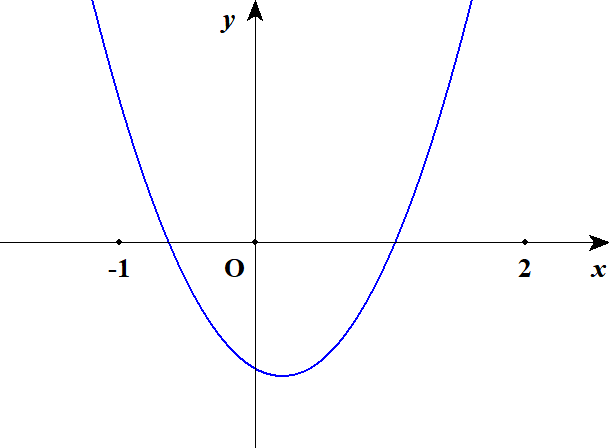
まず原点の左側と右側に1つずつ実数解が存在することから,\(f(0) < 0\)という条件が必要です。 また,左側の解は\(x = -1\)の右側,右側の解は\(x = 2\)の左側になければならないので,\(f(-1)\),\(f(2)\)は\(f(0)\)と異なる符号である必要があります。 つまり,\(f(-1) > 0\),\(f(2) > 0\)という条件が必要になります。
逆に\(f(0) < 0\),\(f(-1) > 0\),\(f(2) > 0\)の3条件があれば題意が満たされることがグラフから分かります。 したがって,この3条件を満たす\(a\)の範囲を求めれば良いですね。
まず\(f(0) < 0\)を解きましょう。
次に\(f(-1) > 0\)を解きましょう。
最後に\(f(2) > 0\)を解きましょう。
以上で求めた3つの範囲の共通部分をとることで,題意を満たす\(a\)の範囲が次のようになることが分かります。
次の2次関数\(f(x)\)について,2次方程式\(f(x) = 0\)が異なる2つの実数解を持ち,片方の解のみが\(1 < x < 2\)の範囲にあるとき,定数\(a\)の値の範囲がどうなるか答えてください。
答え
一見\(f(1)f(2) < 0\)という条件を考えれば良さそうな気がします。 検討してみましょう。
このとき\(f(1)\)と\(f(2)\)は異符号ですから,\(1 < x < 2\)の範囲でグラフが\(x\)軸をまたぐことが保証されます。 もちろんまたぐのは1回だけです。 2回またいだら\(f(x)\)の符号が元に戻って\(f(1)\)も\(f(2)\)も同符号になるからですね。
また,このときグラフは\(x\)軸に接しませんから,実数解は1つではなく,異なる2つのものをとります。 以上から,確かに\(f(1)f(2) < 0\)という条件を満たせば,題意の条件が満たされるようです。
しかし本文でも説明した通り,これは十分条件ではありますが,必要条件ではありません。 言い換えれば,この条件を満たしたとき確かに題意の条件を満たしますが,この条件を満たしたときにしか題意の条件を満たさないわけではないのです。
この違いは非常に重要です。 なぜなら必要条件を拾えていないということは,他にも題意の条件を満たす場合があるかもしれないということだからです。 つまり解答がまだ足りないのです。
では必要条件ではないという点について詳しく調べていきましょう。 題意の条件を満たすとき,グラフは次のような形になります。
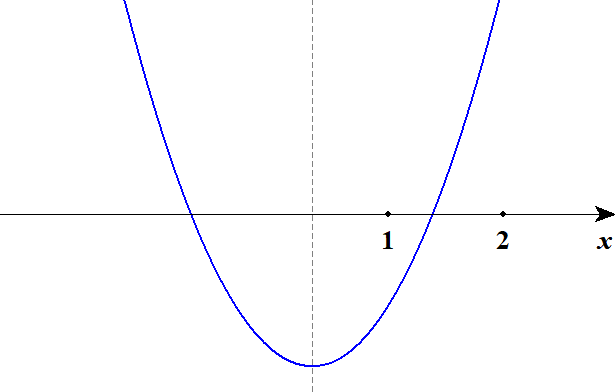
または次のような形もありますね。

この図をみると\(f(1)f(2) < 0\)という条件が必要にも見えます。 しかしちょっとだけ例外があります。 グラフが\(x\)軸をちょうど\(x = 1\)や\(x = 2\)でまたぐ場合です。
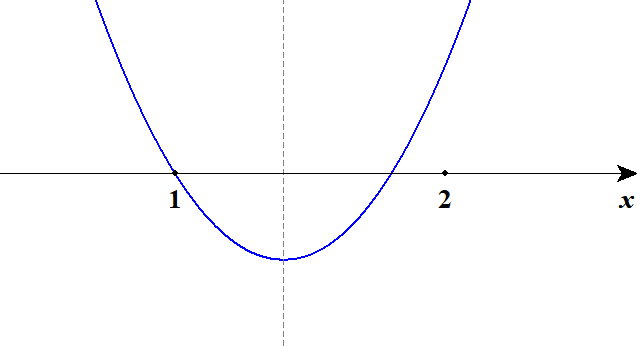
これは\(f(1)f(2) = 0\)であり,\(f(1)f(2) < 0\)という条件は満たさないものの題意の条件は満たす場合です。 このような場合も含めて考えれば,やっとすべてのパターンについて検討できたことになります。
これらの例外パターンについては,満たすべき条件を考えるというよりも,\(f(1) = 0\)や\(f(2) = 0\)の場合を具体的に検討してみると良いです。 このとき\(a\)の値が具体的に決まりますから,2次方程式を解いてみて,もう一方の解が\(1 < x < 2\)を満たすかどうか確かめれば良いのです。
以上で問題の解き方が分かりました。 まずは\(f(1)f(2) < 0\)を解きます。
次に例外パターンその1である\(f(1) = 0\)の場合を考えます。 このとき,\(a\)が次のように決まります。
このとき2次方程式\(f(x) = 0\)は次のように解けます。 \(x = 1\)が解であることが分かっているので,因数分解は簡単です。
\(x = 1\)でない解は\(x = \displaystyle\frac{7}{3}\)であり,\(1 < x < 2\)を満たさないので,\(a = \displaystyle\frac{5}{3}\)は題意の条件を満たしません。
最後に例外パターンその2である\(f(2) = 0\)の場合を考えます。 このとき,\(a\)が次のように決まります。
このとき2次方程式\(f(x) = 0\)は次のように解けます。
この解は\(1 < x < 2\)を満たさないので,\(a = 2\)は題意の条件を満たしません。
以上から,題意を満たす\(a\)の範囲が次のようになることが分かります。
次の2次関数\(f(x)\)について,2次方程式\(f(x) = 0\)が\(-1 < x < 3\)の範囲に異なる2つの実数解を持つとき,定数\(a\)の値の範囲がどうなるか答えてください。
答え
グラフの形を考えてみましょう。 グラフを観察して必要な条件を洗い出します。
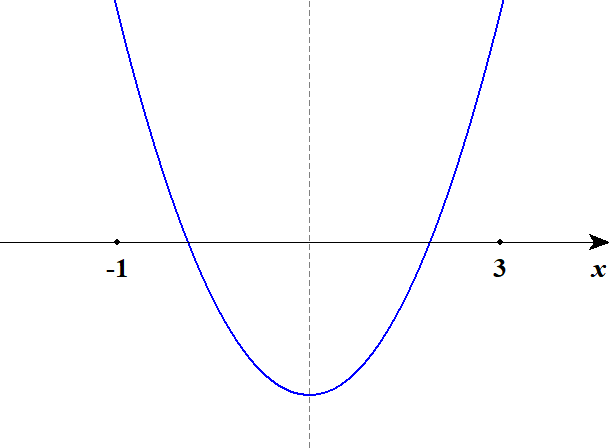
まず異なる2つの実数解を持つことから,判別式が正である必要があります。 また,グラフの軸は\(-1 < x < 3\)の範囲にある必要があるでしょう。 この2つの条件により,グラフの頂点は\(-1 < x < 3\)の範囲にあり,かつ\(x\)軸より下側にあることになります。
あとはこのグラフが\(x\)軸をまたぐ点が\(-1 < x < 3\)の範囲にあれば良いですね。 \(x\)軸をまたぐと\(f(x)\)の符号が変わることを思い出してください。 このことと頂点での値が負であることを考慮すると,\(f(-1)\),\(f(3)\)が正であることが必要だと分かります。
まとめると,判別式\(> 0\),\(-1 <\)軸\(< 3\),\(f(-1) > 0\),\(f(3) > 0\)という条件が必要です。 逆にこれら4条件があれば題意が満たされることがグラフから分かります。 したがって,これらの不等式を解いて\(a\)の範囲を求めれば良いですね。
あらかじめ判別式と軸を計算しておきましょう。 判別式は次の通りです。
軸は,次の平方完成の通り\(x = 2a\)です。
まず判別式\(> 0\)を解きます。
次に\(-1 <\)軸\(< 3\)を解きます。
次に\(f(-1) > 0\)を解きます。
最後に\(f(3) > 0\)を解きます。
以上で求めた4つの範囲の共通部分をとることで,題意を満たす\(a\)の範囲が次のようになることが分かります。
