前回は素直に解くだけの2次不等式を扱いました。 今回扱う問題は,もっとグラフを駆使して考える必要のあるものです。 グラフの特徴を簡潔にとらえられるように練習しましょう。
目次
グラフと\(x\)軸
不等式を考えるときは,まず項を片方の辺に集めて「整式\(< 0\)」や「整式\(> 0\)」のような形にします。 定数\(0\)は,グラフとしては\(x\)軸を表しますから,左辺のグラフと\(x\)軸の共有点や上下関係を調べることで不等式を解くことができます。
今回扱うのは整式が2次式になる場合ですから,左辺のグラフは放物線です。 放物線と\(x\)軸の位置関係は,「上に凸か下に凸か」と「判別式\(D\)の符号」で分かります。
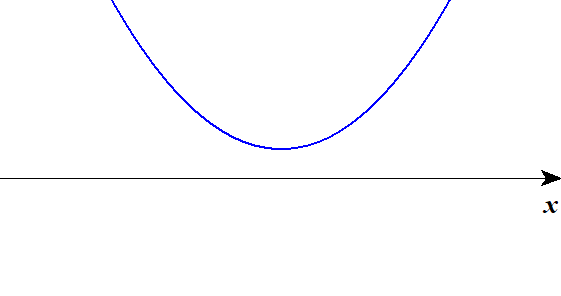
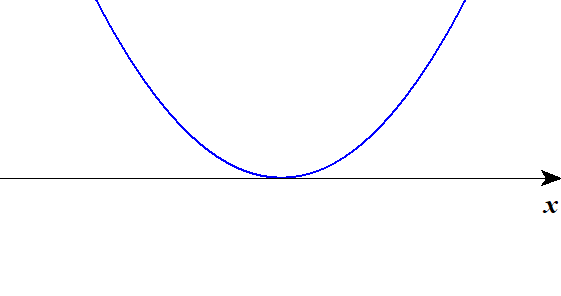
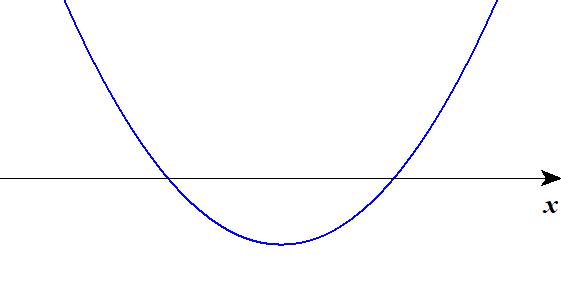
■ 下に凸
| \(D < 0\) | \(D = 0\) | \(D > 0\) |
|---|---|---|
 |
 |
 |
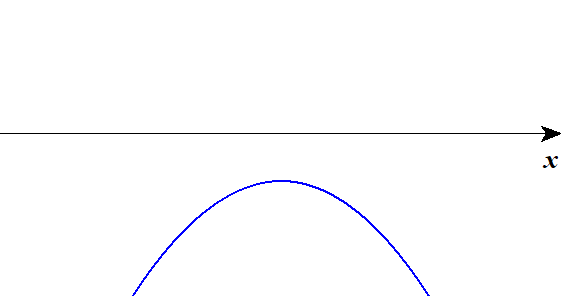
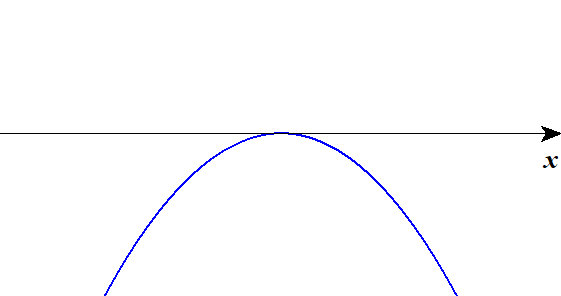
■ 上に凸
| \(D < 0\) | \(D = 0\) | \(D > 0\) |
|---|---|---|
 |
 |
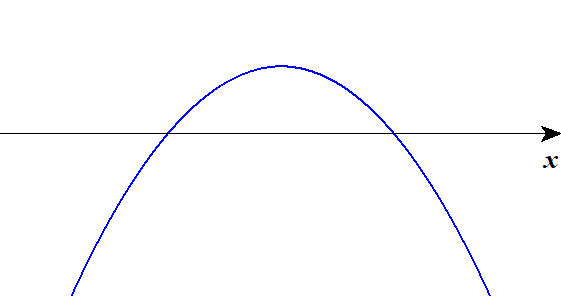 |
放物線と\(x\)軸の位置関係は,丸暗記するものではありません。 「放物線が上下どっち向きか」と「\(x\)軸との共有点がいくつか」を考えれば,自然と上表の形にたどり着きます。 覚えるのではなく,納得しましょう。
最大値・最小値と不等式
現実的な問題を考えると,不等式をただ解くだけでは物足りません。 寧ろある不等式が常に成立するように,関数を改善したいです。 例えば「売上が常に一定額以上になるように」とか。
こういった「常に」や「いつも」を考えるときは,関数の最大値・最小値の情報が役に立ちます。 「最も悪いときでもセーフ」になるようにすると考えるのです。 例えば「売上が最も悪いとき(最小値)でも目標額以上になるように」とか。
つまり,常にある値を上回りたいなら,最小値がその値を上回れば良く,常にある値を下回りたいなら,最大値がその値を下回れば良いわけです。 こう考えると「常に」の問題を「最大値・最小値を求める問題」と「不等式の問題」にうまく分解できます。
この例では「常に上回る/下回る」を考えたので,最大値・最小値の問題に言い換えられました。 このような「代表値」は問題の内容によって異なりますから,いろいろな問題に挑戦して考えてみましょう。
確認問題
Aさんは\(500\)円の価値をもつグッズを\(300\)個もっています。 Aさんは現金が尽きたのでグッズを売り払うことにしましたが,どうやら\(1\)個売るたびにグッズの価値が\(1\)円下がるようです。 Aさんは初め\(150000\)円の総価値をもっていたわけですが,グッズを売るたびに総価値はどんどん減ってしまいます。
Aさんはある程度の価値を手元に残しておきたいと思いました。 具体的には\(30000\)円~\(80000\)円の総価値だけを残しておくことにしました。
Aさんはグッズを最低でもいくつ売らなければならないでしょうか? また,最高で何個まで売っても良いでしょうか?
答え
グッズを売る数が問題ですから,これを\(x\)個とおきましょう。 問題の条件を\(x\)の不等式で表して解きましょう。 \(x\)のとれる範囲は\(0 \leqq x \leqq 300\)ですね。
残す総価値についての条件がありますから,残った総価値を\(y\)とおくと,これは次の式で表せます。
問題の条件は\(30000 \leqq y \leqq 80000\)ですから,次の連立不等式を解けば良いですね。
まず2つめの式を解きます。 不等式を整理すると次のようになります。
これを解くと\(x \leqq 200, \ 600 \leqq x\)ですね。
次は3つめの式を解きます。 不等式を整理すると次のようになります。
これを解くと\(100 \leqq x \leqq 700\)です。
以上から\(x\)の範囲の共通部分をとると,\(100 \leqq x \leqq 200\)になります。 したがって,グッズを売る個数は最低\(100\)個,最高\(200\)個です。
Aさんは初め\(M\)万円のお金をもっています。 Aさんは毎秒お金のやり取りをしており,\(x\)秒後には総支出が\(3x + 5\)万円,総収入が\(x^2 + x\)万円になります。
Aさんのお金が一瞬でも\(0\)未満にならないようにするには,\(M\)の値の範囲がいくつであれば良いでしょうか?
答え
Aさんのお金が\(0\)未満にならないようにしたいので,Aさんの残金に注目しましょう。 \(x\)秒後のAさんの残金を\(y\)万円とすると,\(y\)は次のようになります。
残金が\(0\)未満にならないようにするには,\(y\)の最小値が\(0\)以上になれば良いですね。 \(x\)のとりうる範囲が\(x \geqq 0\)であることに注意して,最小値を求めましょう。
まずは次のように平方完成します。
これでグラフの軸が\(x = 1\)であることが分かりました。 軸が定義域内に含まれているので,最小値は頂点でとり,\(M - 6\)です。 これが\(0\)以上であれば良いので,\(M \geqq 6\)であれば良いことが分かりました。
\(0 \leqq x \leqq 2\)を定義域とする関数\(y = x^2 - 2ax + 1\)が,定義域内で常に\(0\)以上であるとき,\(a\)の値の範囲を求めてください。
答え
「常に\(0\)以上」は「最小値が\(0\)以上」と言い換えられます。 まず最小値を求め,「最小値\(\geqq 0\)」という不等式を解けば良いですね。
最小値を考えるため,放物線の軸と定義域の位置関係を把握したいです。 まずは関数式を平方完成して軸を求めましょう。
これで軸が\(x = a\)であることが分かりました。
最小値は,軸が定義域内にあるとき頂点でとり,定義域外にあるときは定義域の端のうち軸から近い方でとります。 したがって,最小値は次のように場合分けして考えられます。
[1] \(a < 0\)のとき:
このとき,軸は定義域の左外側にあるため,最小値は\(x = 0\)でとります。 よって,最小値は\(1\)になりますが,これは\(a\)の値に関わらず\(0\)以上ですね。 したがって,\(a < 0\)のときは常に問題の条件を満たします。
[2] \(0 \leqq a \leqq 2\)のとき:
このとき,軸は定義域内にあるため,最小値は頂点でとります。 よって,最小値は\(-a^2 + 1\)になりますから,問題の条件を満たすためには,次の不等式を考えれば良いです。
この不等式の解は\(-1 \leqq a \leqq 1\)ですから,\(0 \leqq a \leqq 2\)との共通範囲をとると,\(0 \leqq a \leqq 1\)のときに問題の条件を満たすことが分かります。
[3] \(2 < a\)のとき:
このとき,軸は定義域の右外側にあるため,最小値は\(x = 2\)でとります。 よって,最小値は\(-4a + 5\)になりますから,問題の条件を満たすためには,次の不等式を考えれば良いです。
この不等式の解\(a \leqq \displaystyle\frac{5}{4}\)と\(2 < a\)には共通範囲がありませんから,\(2 < a\)のときは問題の条件を満たさないことが分かります。
以上,[1]~[3]から,問題の条件を満たす\(a\)の範囲は\(a \leqq 1\)であることが分かりました。
