前回まで,2次関数がある特定の値をとるのがいつかを考える2次方程式を学びました。 しかし現実の問題では,特定の値をぴったりとるなんて特殊な状況よりも,その値を上回るか下回るかという大小関係に興味があることが多いです。 それを考えるのが不等式です。
目次
グラフと不等式
今までに扱った不等式といえば1次不等式ですが,これは簡単な式変形で解くことができました。 しかしどんな不等式にも対応できるようにするためには,グラフを駆使する必要があります。
次の図を見てください。 とある関数\(f(x), g(x)\)のグラフです。
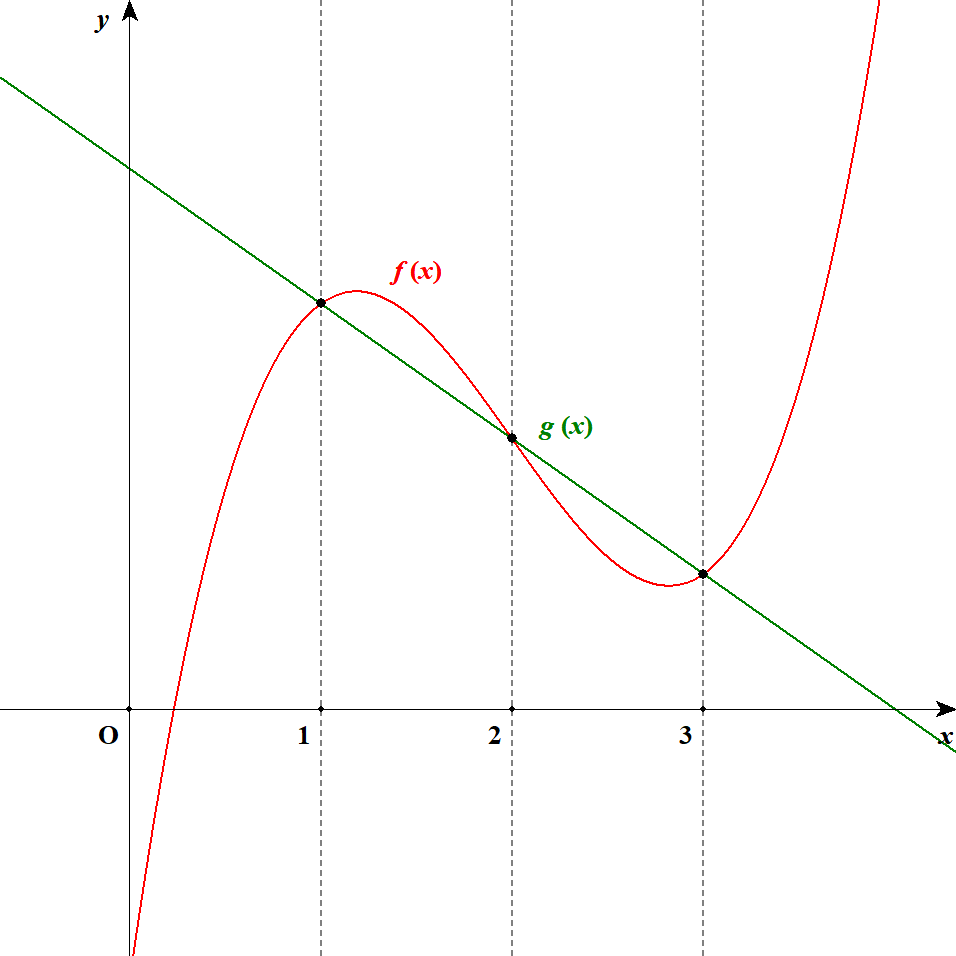
このグラフを使って不等式\(f(x) < g(x)\)を考えてみましょう。 この不等式は\(g(x)\)が\(f(x)\)よりも大きくなる\(x\)の範囲を求めるものですね。
\(g(x)\)が\(f(x)\)よりも大きい範囲は,グラフを見れば分かります。 \(g(x)\)の方が上側にある範囲を探せば良いですね。 グラフを見ると,その範囲は\(x < 1, \ 2 < x < 3\)であることが分かります。 これが不等式の解です。
このように,不等式を解くには,グラフをかいてその上下関係を比較すれば良いです。
また上図のグラフに\(y\)座標が書かれていないように,不等式を解く際に具体的な\(y\)座標は必要ありません。 グラフの概形と共有点の\(x\)座標の情報しか使いませんでしたね。 不等式のためにかくグラフは簡単で良いのです。
2次不等式
それでは今回の本題,2次不等式に入りましょう。 2次不等式は次のような形の不等式ですね。
不等式を解くには,前項で見た通り,右辺と左辺のグラフを比較するのですが,上式のように右辺は常に\(0\)にしておきましょう。 そうすれば,左辺のグラフが\(x\)軸より上にあるか下にあるかを調べるだけで済むからです。
例として次の不等式を解きましょう。
不等式を解くためにグラフをかくのですが,しっかりしたグラフは必要ありません。 下図程度で十分です。
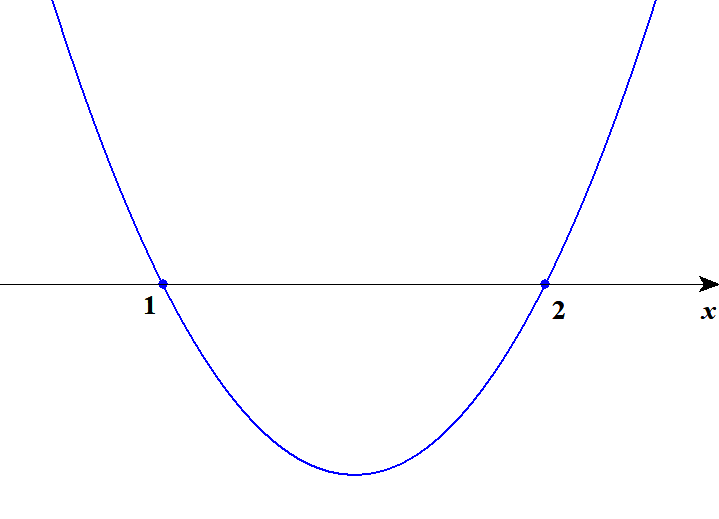
グラフにかいたのは,グラフの概形と\(x\)切片の\(x\)座標だけです。 かなりシンプルですが,これだけでグラフと\(x\)軸の上下関係がはっきりしていますね。
\(x^2 - 3x + 2 \leqq 0\)である範囲を強調すると,下図のようになります。 \(x\)軸の下側にある部分ですね。 不等号に\(=\)がついているので,端点は黒丸で表します。(青いけど)
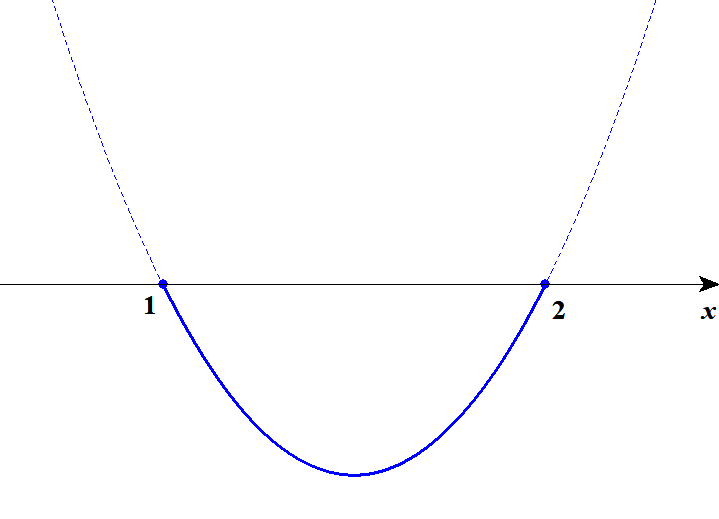
この図から,不等式の解が\(1 \leqq x \leqq 2\)であることが分かります。
もうひとつ例を見ておきましょう。 次の不等式を解きます。
グラフは次のようになります。
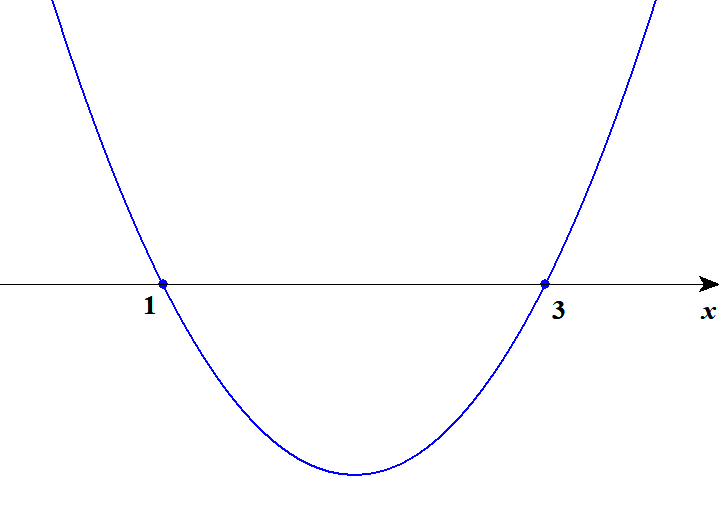
\(x^2 - 4x + 3 > 0\)である範囲は,グラフが\(x\)軸より上側にある部分です。 この範囲を強調すると,下図のようになります。 不等号に\(=\)がついていないので,端点は白丸で表します。
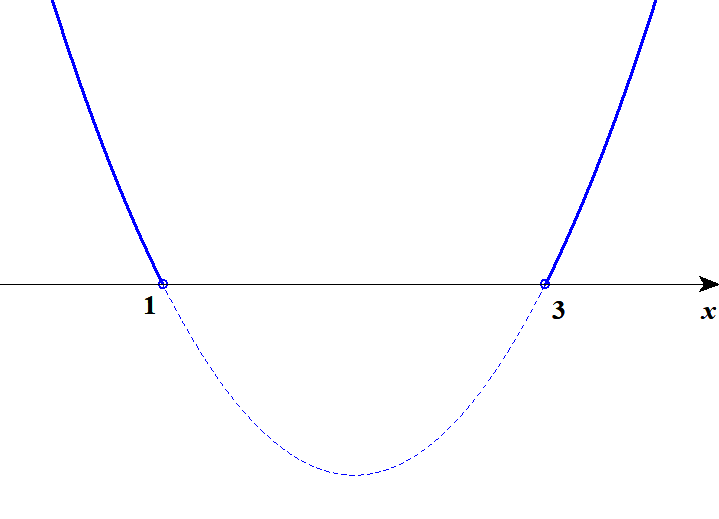
この図から,不等式の解が\(x < 1, \ 3 < x\)であることが分かります。 不等号の向きをそろえるため,\(x < 1, \ x > 3\)という書き方はしないことが多いです。
上の例では,2次関数のグラフがすべて下に凸でした。 2次関数のグラフが上に凸の場合も同じように解けますが,不等式の両辺を\(-1\)倍すれば,下に凸のグラフで考えることもできます。
また,確認問題でグラフが\(x\)切片をもたない場合なども扱います。 これらの解法を個別にパターン化して覚える必要は一切ありません。 ささっとグラフをかいて確認できるように練習しましょう。
確認問題
次の2次不等式を解いてください。
-
\(x(x + 1) < 2\)
-
\(x^2 - 4 \geqq -2x + 4\)
-
\(2x - x^2 \leqq 0\)
-
\(7x - 3 > 2x^2\)
答え
\(x\)切片を求め,簡単なグラフをかいて解きましょう。
-
式を整理すると次のようになります。
\( \begin{align} x(x + 1) &< 2 \\[5pt] x^2 + x &< 2 \\[5pt] x^2 + x - 2 &< 0 \\[5pt] (x - 1)(x + 2) &< 0 \end{align} \)グラフは次のようになります。
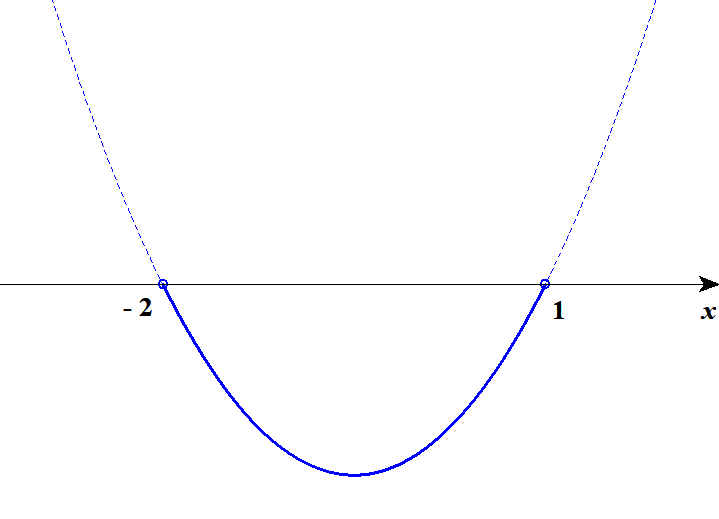
グラフより,この不等式の解は\(-2 < x < 1\)です。
-
式を整理すると次のようになります。
\( \begin{align} x^2 - 4 &\geqq -2x + 4 \\[5pt] x^2 + 2x - 8 &\geqq 0 \\[5pt] (x - 2)(x + 4) &\geqq 0 \end{align} \)グラフは次のようになります。
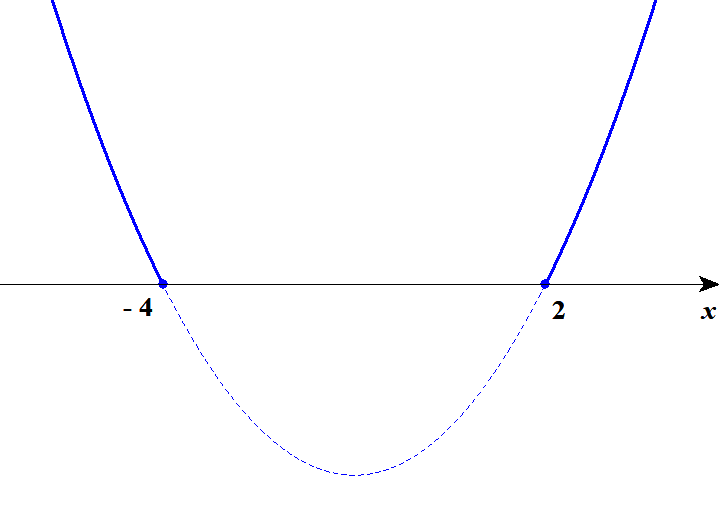
グラフより,この不等式の解は\(x \leqq -4, \ 2 \leqq x\)です。
-
式を整理すると次のようになります。
\( \begin{align} 2x - x^2 &\leqq 0 \\[5pt] x^2 - 2x &\geqq 0 \\[5pt] x(x - 2) &\geqq 0 \end{align} \)グラフは次のようになります。
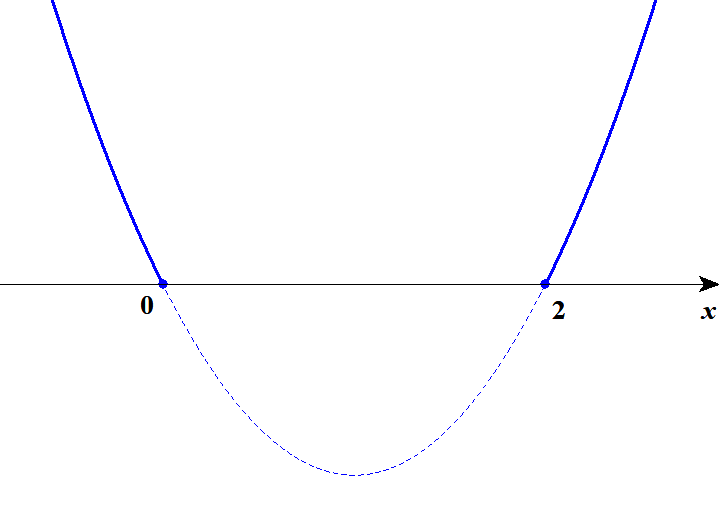
グラフより,この不等式の解は\(x \leqq 0, \ 2 \leqq x\)です。
-
式を整理すると次のようになります。
\( \begin{align} 7x - 3 &> 2x^2 \\[5pt] 2x^2 - 7x + 3 &< 0 \\[5pt] (x - 3)(2x - 1) &< 0 \end{align} \)グラフは次のようになります。
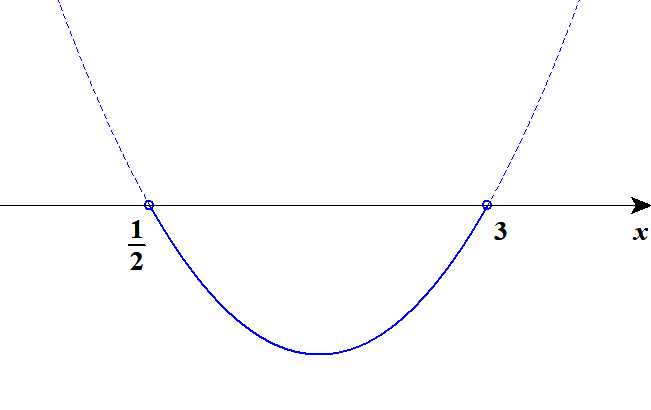
グラフより,この不等式の解は\(\displaystyle\frac{1}{2} < x < 3\)です。
次の2次不等式を解いてください。
-
\(x^2 - 2x + 2 \geqq 0\)
-
\(x^2 - 4x + 4 \leqq 0\)
-
\(x^2 - 4x + 4 < 0\)
答え
この問題では,\(x\)切片を求めようとすると,実数解が2個ないことに気が付きます。 グラフと\(x\)軸の位置関係がどうなるかに注意しましょう。
-
左辺の判別式\(D\)は次のようになります。
\( \begin{align} D &= (-2)^2 - 4 \cdot 1 \cdot 2 \\[5pt] &= -4 < 0 \end{align} \)判別式が負ですから,このグラフに\(x\)切片はありません。 この放物線が下に凸であることも考慮すると,グラフは次のようになります。
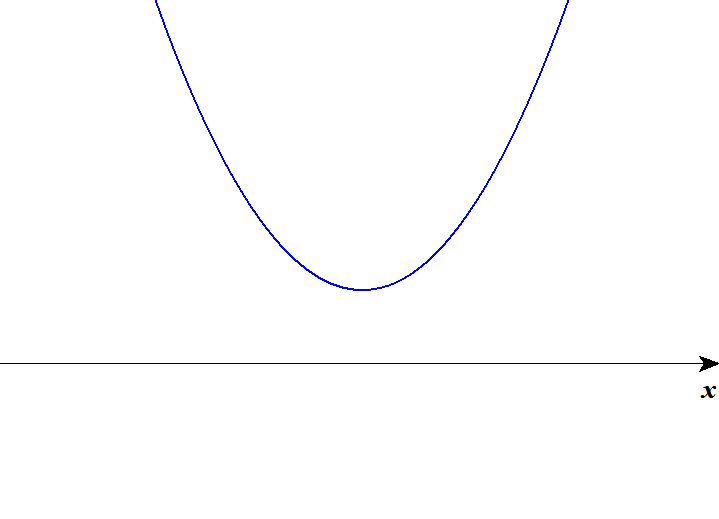
グラフはどこをとっても\(x\)軸の上側にありますから,この不等式の解はすべての実数です。
-
不等式を整理すると次のようになります。
\( \begin{align} x^2 - 4x + 4 &\leqq 0 \\[5pt] (x - 2)^2 &\leqq 0 \end{align} \)\(x\)切片が1つだけですから,この放物線が下に凸であることも考慮すると,グラフは次のように\(x\)軸に接します。
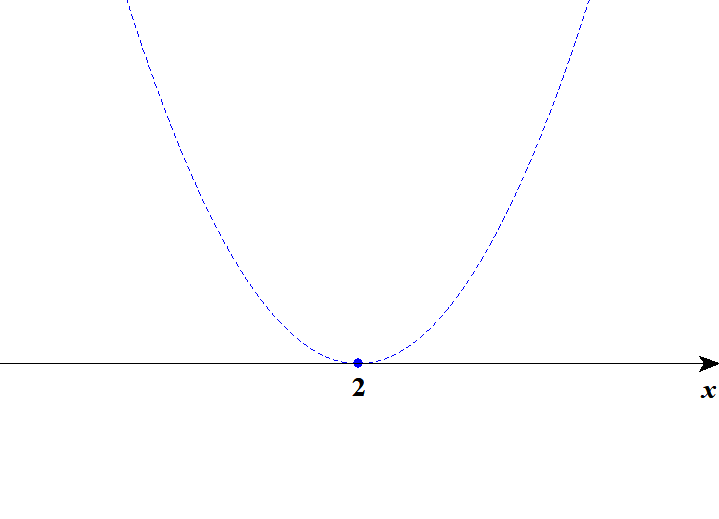
グラフが\(x\)軸より小さい部分は一切ありませんが,不等号が\(=\)を含んでいるので,接点はギリギリ不等式を満たします。 したがって,この不等式の解は\(x = 2\)です。
-
不等式を整理すると次のようになります。
\( \begin{align} x^2 - 4x + 4 &< 0 \\[5pt] (x - 2)^2 &< 0 \end{align} \)\(x\)切片が1つだけですから,この放物線が下に凸であることも考慮すると,グラフは次のように\(x\)軸に接します。
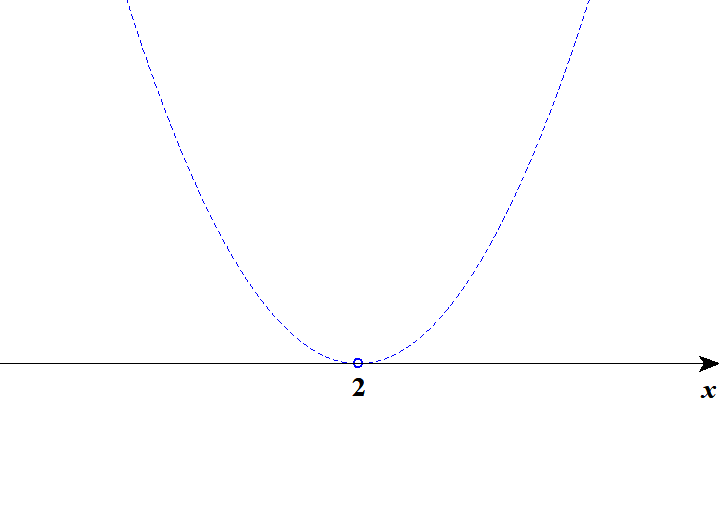
グラフが\(x\)軸より小さい部分は一切ないので,この不等式は解なしです。
次の連立不等式を解いてください。
答え
まずそれぞれの不等式を解き,それらの解の共通部分を求めましょう。
1つめの不等式を整理すると次のようになります。
今までの繰り返しになるのでグラフは省略しますが,この不等式の解は\(x \leqq 0, \ 1 \leqq x\)です。
次に2つめの不等式を整理すると次のようになります。
今までの繰り返しになるのでグラフは省略しますが,この不等式の解は\(x < 2, \ 3 < x\)です。
これらを図示すると次のようになります。 1つめの不等式の解を青色,2つめの不等式の解を赤色で表しています。
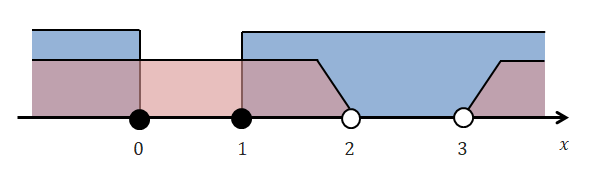
連立方程式の解はこれらの共通範囲です。 したがって,上図より解は\(x \leqq 0\),\(1 \leqq x < 2\),\(3 < x\)です。
