2次方程式は2次式の方程式ですから,これはもちろん2次関数とも関係があります。 前回までで2次方程式の解や,その個数を考えられるようになりましたが,今回はそれを2次関数のグラフにも応用しましょう。
目次
2次方程式と放物線
2次方程式\(ax^2 + bx + c = 0\)は,2次関数\(y = ax^2 + bx + c\)の値が\(0\)になるような\(x\),つまり\(x\)切片を求める方程式です。 その\(x\)の個数は判別式で調べられました。
下に凸の放物線を例として,判別式とグラフの関係を見てみましょう。 上に凸の場合は,グラフが上下反転した形になります。 判別式を\(D = b^2 - 4ac\)とします。
| 判別式 | \(x\)切片の数 | グラフ |
|---|---|---|
| \(D > 0\) | \(2\) | 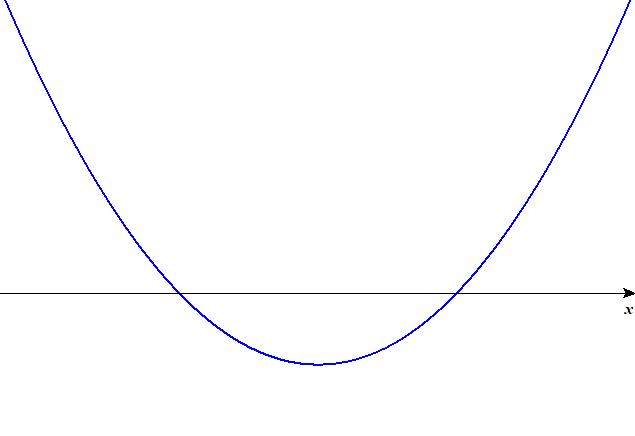 |
| \(D = 0\) | \(1\) | 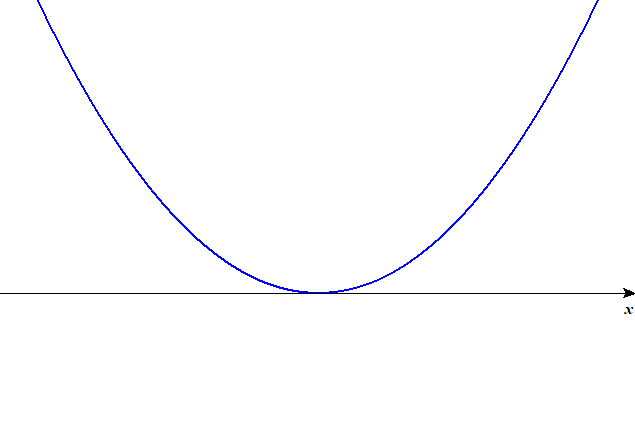 |
| \(D < 0\) | \(0\) | 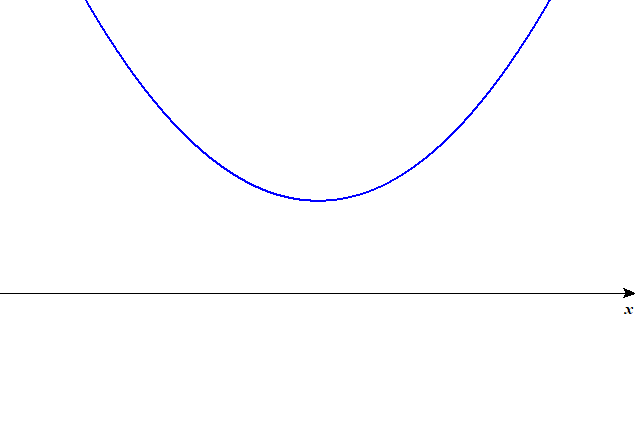 |
上表の通り,\(D > 0\)のときは2次方程式の実数解が2個ありますから,グラフの\(x\)切片も2個あります。 放物線の\(x\)切片が2個ということは,図のように\(x\)軸をまたぐ形になるわけですね。
\(D = 0\)のときは\(x\)切片が1つだけで,放物線の頂点がちょうど\(x\)軸に乗る形になります。 このとき,放物線は\(x\)軸に接するといい,接している点を接点といいます。
\(D < 0\)のときは\(x\)切片がありません。 放物線が\(x\)軸に全く触れないわけですから,図のようになります。
\(x\)切片の座標は分かりますね。 2次方程式\(ax^2 + bx + c = 0\)の実数解です。 念のため解の公式を書いておきます。
放物線と直線
複数のグラフを同時に考えてみましょう。 特にここでは,放物線と直線を同時に考えます。 次のようなグラフになります。
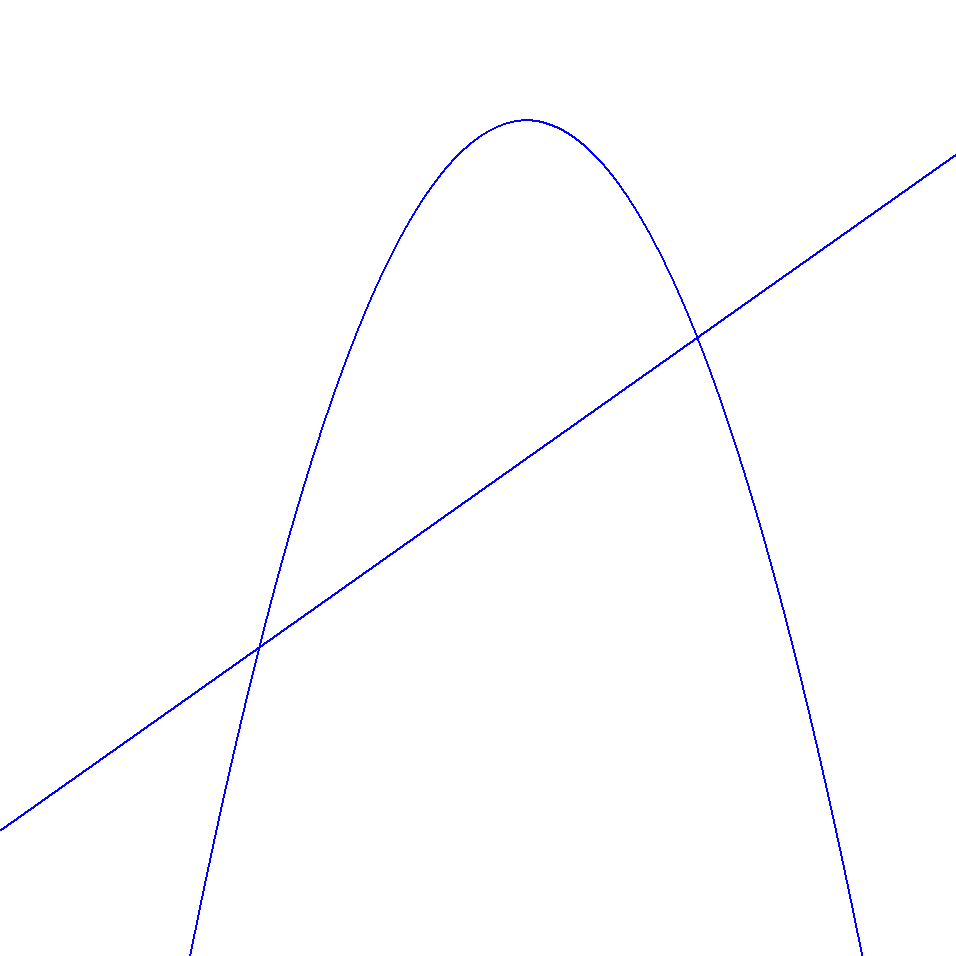
このグラフでは,放物線と直線のぶつかる点が2つあり,この点を共有点といいます。 複数のグラフを考えるときに重要なのは,「共有点がどこか」や「いつどちらの関数の方が大きな値をとるか」といった情報です。
関数の大小関係については,次回から学ぶ不等式を使って考えます。 ここでは,共有点の求め方を学びましょう。
例として,直線\(y = 2x + 1\)と放物線\(y = x^2 + 3x - 1\)の共有点を考えましょう。 共有点は,直線上の点であり,放物線上の点でもあります。 つまり,共有点はどちらの方程式も満たす点なのですから,次の連立方程式を考えれば共有点を求められます。
1つめの式を2つめの式に代入して整理すると,次の方程式が得られます。
方程式を解くことで,共有点の\(x\)座標が\(-2, 1\)の2つあることが分かります。 この\(x\)の値を\(y = 2x + 1\)に代入することで\(y\)座標も求められます。 (2つめの式の方に代入してもOKです。)
よって,この2つのグラフの共有点が,点\((-2, -3), (1, 3)\)であることが分かりました。
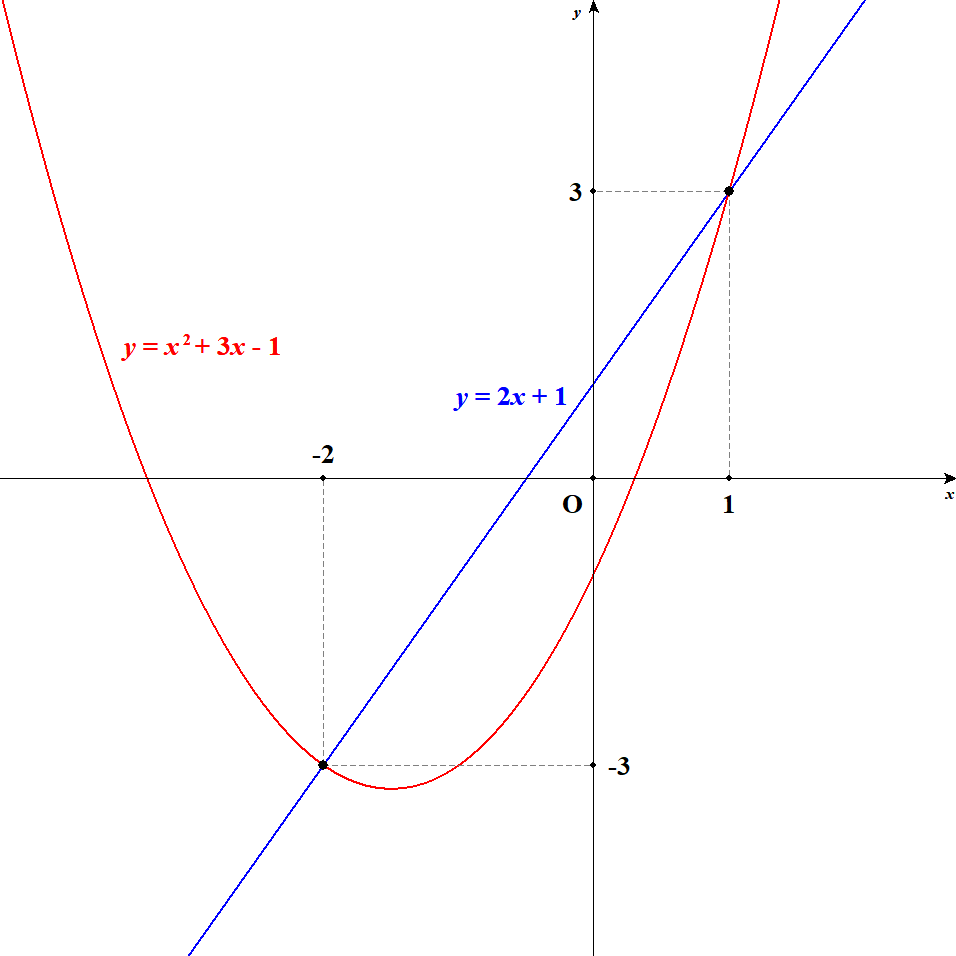
このように,グラフの共有点を調べるには,グラフの方程式を連立させて解くことになります。
共有点の個数
次は共有点の個数の調べ方を学びましょう。 「個数だけ調べる意味ある?」と思うかもしれませんが,グラフがいつ共有点をもつか,いつ接するかというのは重要な情報です。
共有点の座標を求めるとき,関数式を連立させて解きました。 片方の式をもう一方の式に代入してできる方程式を解けば,座標が得られるのですが,共有点の個数を調べるだけなら解く必要はありません。 判別式を調べれば良いですね。
ここで改めて前項で考えたグラフを例に考えてみましょう。 直線\(y = 2x + 1\)と放物線\(y = x^2 + 3x - 1\)です。 共有点を求める連立方程式は次の通りになります。
1つめの式を2つめの式に代入すると,次の方程式が得られました。
共有点の座標を求めるときは方程式を解くのですが,個数を調べるだけなら判別式を計算すればOKです。 判別式\(D\)は次の通りです。
判別式が正であることから,方程式の実数解は2個あるので,共有点の個数が2であることが分かりました。
確認問題
次の2次関数のグラフをかいてください。 ただし頂点,\(x\)切片,\(y\)切片の座標は明記してください。
-
\(y = x^2 - 2x + 1\)
-
\(y = x^2 - 4x - 2\)
-
\(y = 2x^2 - 5x + 2\)
答え
\(x = 0\)とすれば\(y\)切片が,\(y = 0\)とすれば\(x\)切片が,平方完成すれば頂点が分かります。 \(x\)切片を求めるには2次方程式を解く必要があります。
-
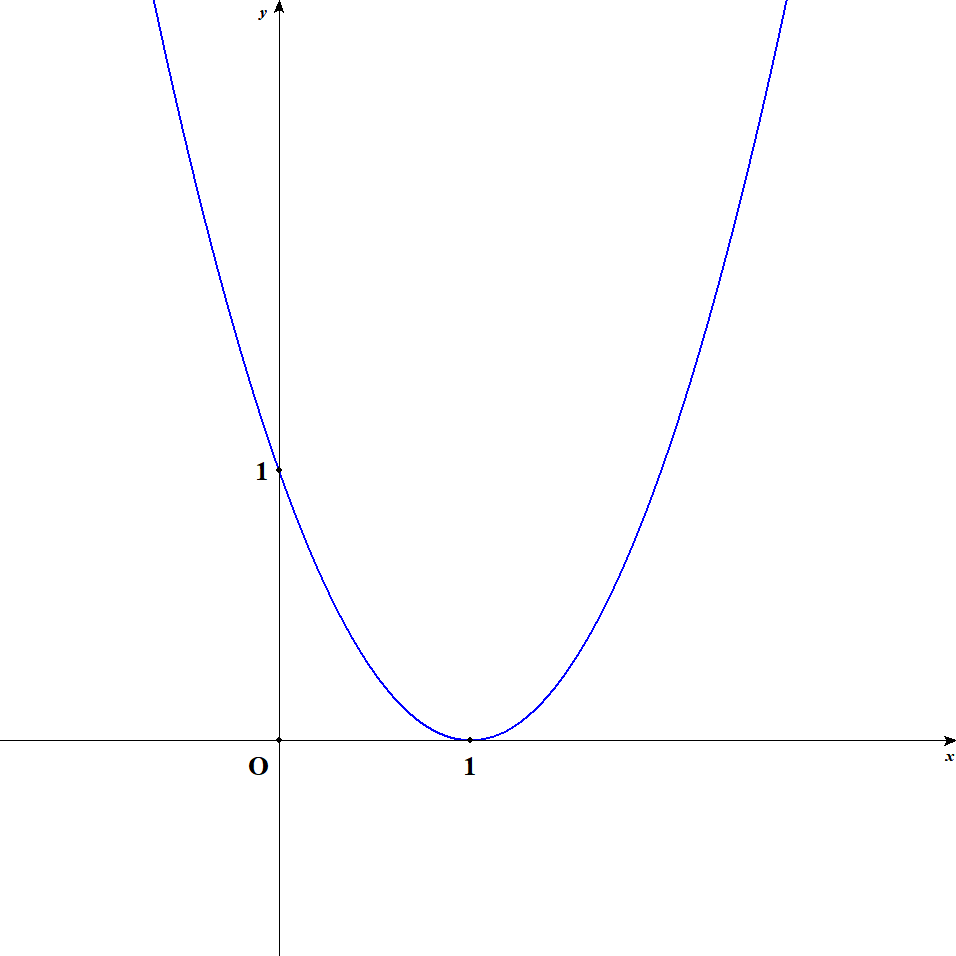
平方完成すると次のようになるので,頂点は点\((1, 0)\)です。
\( \begin{align} y &= x^2 - 2x + 1 \\[5pt] &= (x - 1)^2 \end{align} \)\(x = 0\)とすると,\(y\)切片が点\((0, 1)\)であると分かります。 次に\(y = 0\)として2次方程式を解き,\(x\)切片を求めます。
\( \begin{align} x^2 - 2x + 1 &= 0 \\[5pt] (x - 1)^2 &= 0 \\[5pt] x &= 1 \end{align} \)これで\(x\)切片が点\((1, 0)\)であると分かりました。 以上から,グラフは次のようになります。
-
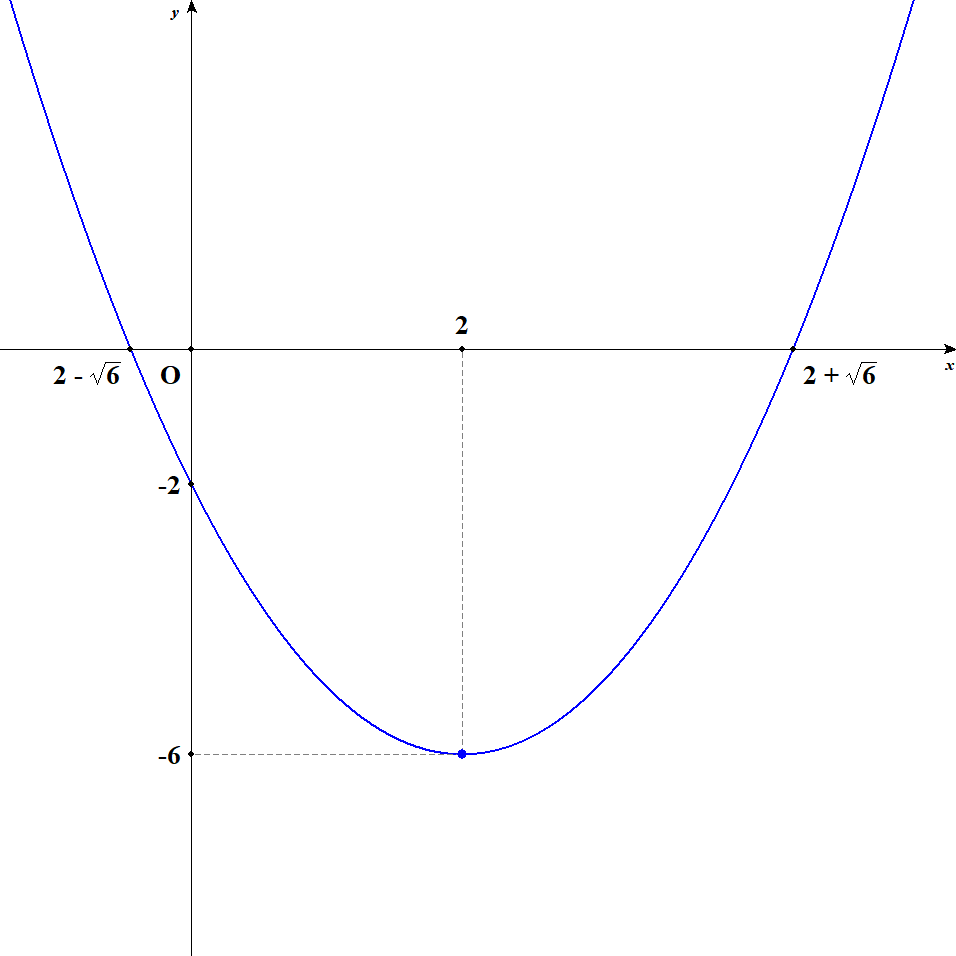
平方完成すると次のようになるので,頂点は点\((2, -6)\)です。
\( \begin{align} y &= x^2 - 4x - 2 \\[5pt] &= (x - 2)^2 - 6 \end{align} \)\(x = 0\)とすると,\(y\)切片が点\((0, -2)\)であると分かります。 次に\(y = 0\)として2次方程式を解き,\(x\)切片を求めます。
\( \begin{align} x^2 - 4x - 2 = 0 \end{align} \)\( \begin{align} x &= -(-2) \pm \sqrt{(-2)^2 - 1 \cdot (-2)} \\[5pt] &= 2 \pm \sqrt{6} \end{align} \)これで\(x\)切片が点\((2 + \sqrt{6}, 0), (2 - \sqrt{6}, 0)\)であると分かりました。 以上から,グラフは次のようになります。
-
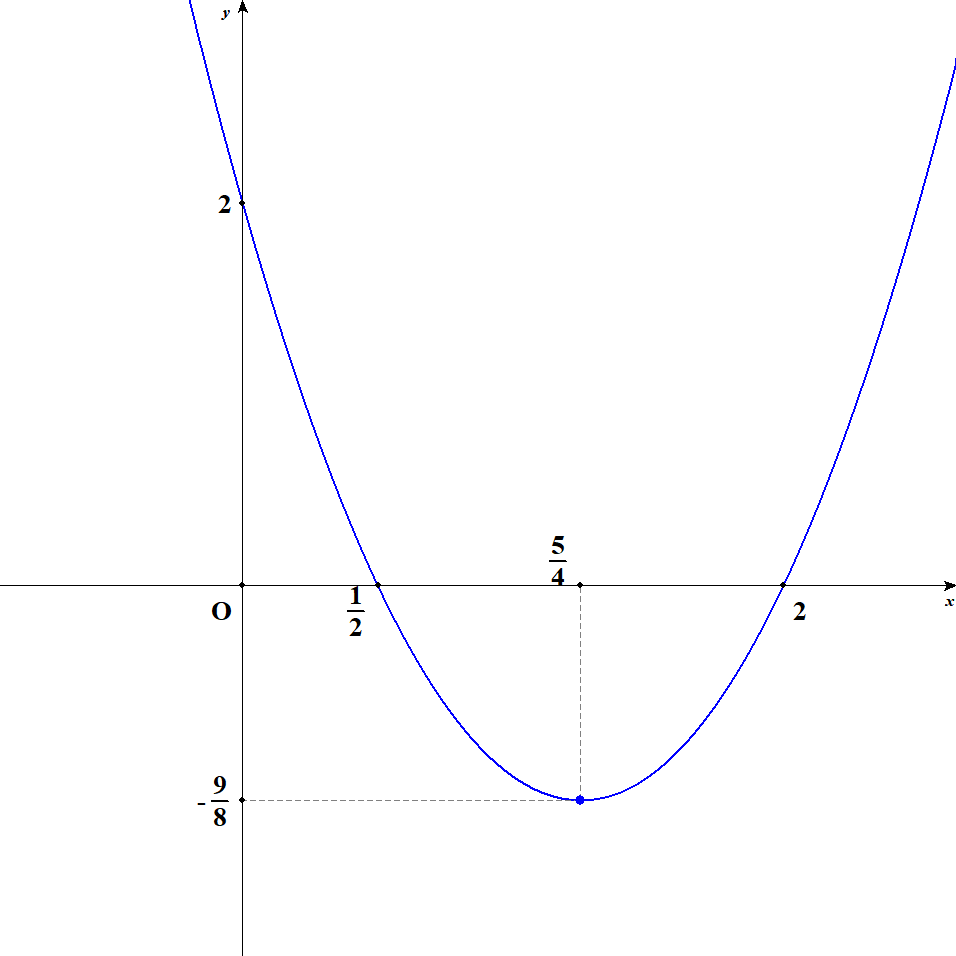
平方完成すると次のようになるので,頂点は点\(\left(\displaystyle\frac{5}{4}, -\displaystyle\frac{9}{8}\right)\)です。
\( \begin{align} y &= 2x^2 - 5x + 2 \\[5pt] &= 2\left(x^2 - \displaystyle\frac{5}{2}x\right) + 2 \\[5pt] &= 2\left(x - \displaystyle\frac{5}{4}\right)^2 - 2 \cdot \left(\displaystyle\frac{5}{4}\right)^2+ 2 \\[5pt] &= 2\left(x - \displaystyle\frac{5}{4}\right)^2 - \displaystyle\frac{9}{8} \\[5pt] \end{align} \)\(x = 0\)とすると,\(y\)切片が点\((0, 2)\)であると分かります。 次に\(y = 0\)として2次方程式を解き,\(x\)切片を求めます。
\( \begin{align} 2x^2 - 5x + 2 &= 0 \\[5pt] (x - 2)(2x - 1) &= 0 \\[5pt] x&= \displaystyle\frac{1}{2}, \ 2 \end{align} \)これで\(x\)切片が点\(\left(\displaystyle\frac{1}{2}, 0\right), (2, 0)\)であると分かりました。 以上から,グラフは次のようになります。
次の2つの図形の共有点の座標をそれぞれ求めてください。 ただし,共有点をもたない場合は「共有点をもたない」と答えてください。
-
放物線: \(y = -x^2 - x + 1\)
直線: \(y = -5x + 4\)
-
放物線: \(y = 4x^2 - 9x + 2\)
直線: \(y = 3x - 7\)
-
放物線: \(y = 2x^2 - 5x + 18\)
放物線: \(y = -x^2 + 13x - 9\)
答え
共有点というのは,両方の関数式を満たす点ですから,両方の関数式を連立させて解けば求められます。
-
次の連立方程式を解けば良いです。
\( \begin{eqnarray} \left\{ \begin{array}{l} y &= -x^2 - x + 1 \\ y &= -5x + 4 \end{array} \right. \end{eqnarray} \)2つめの式を1つめに代入し,できた2次方程式を解くことで,共有点の\(x\)座標が求められます。
\( \begin{align} -x^2 - x + 1 &= -5x + 4 \\[5pt] x^2 - 4x + 3 &= 0 \\[5pt] (x - 1)(x - 3) &= 0 \\[5pt] x &= 1, 3 \end{align} \)求めた\(x\)の値を2つめの式に代入し,\(y\)座標を求めます。
\( \begin{align} y &= -5 + 4, \ -15 + 4 \\[5pt] &= -1, \ -11 \end{align} \)以上から,共有点の座標は\((1, -1), \ (3, -11)\)です。
-
次の連立方程式を解けば良いです。
\( \begin{eqnarray} \left\{ \begin{array}{l} y &= 4x^2 - 9x + 2 \\ y &= 3x - 7 \end{array} \right. \end{eqnarray} \)2つめの式を1つめに代入し,できた2次方程式を解くことで,共有点の\(x\)座標が求められます。
\( \begin{align} 4x^2 - 9x + 2 &= 3x - 7 \\[5pt] 4x^2 - 12x + 9 &= 0 \\[5pt] (2x - 3)^2 &= 0 \\[5pt] x &= \displaystyle\frac{3}{2} \end{align} \)求めた\(x\)の値を2つめの式に代入し,\(y\)座標を求めます。
\( \begin{align} y &= \displaystyle\frac{9}{2} - 7 \\[5pt] &= - \displaystyle\frac{5}{2} \end{align} \)以上から,共有点の座標は\(\left(\displaystyle\frac{3}{2}, \ -\displaystyle\frac{5}{2}\right)\)です。
-
次の連立方程式を解けば良いです。
\( \begin{eqnarray} \left\{ \begin{array}{l} y &= 2x^2 - 5x + 18 \\ y &= -x^2 + 13x - 9 \end{array} \right. \end{eqnarray} \)2つめの式を1つめに代入し,できた2次方程式を解くことで,共有点の\(x\)座標が求められます。
\( \begin{align} 2x^2 - 5x + 18 &= -x^2 + 13x - 9 \\[5pt] 3x^2 - 18x + 27 &= 0 \\[5pt] x^2 - 6x + 9 &= 0 \\[5pt] (x - 3)^2 &= 0 \\[5pt] x &= 3 \end{align} \)求めた\(x\)の値を1つめの式に代入し,\(y\)座標を求めます。
\( \begin{align} y &= 2 \cdot 3^2 - 5 \cdot 3 + 18 \\[5pt] &= 18 - 15 + 18 \\[5pt] &= 21 \end{align} \)以上から,共有点の座標は\((3, \ 21)\)です。
次の放物線と直線の共有点がいくつあるか答えてください。 ただし,\(a\)は定数です。
放物線: \(y = 2x^2 + x - 1\)
直線: \(y = 4x - a\)
答え
共有点は両方の関数式を満たす点ですから,両方の関数式を連立させて解けば共有点の座標が分かります。 しかし,今回は座標までは必要ないので,連立方程式からできる2次方程式で判別式を計算しましょう。
共有点を求める連立方程式は次のようになります。
2つめの式を1つめの式に代入して整理します。
共有点の個数だけ考えれば良いので,判別式\(D\)を計算します。
この方程式の解の個数は\(D > 0\)のとき2,\(D = 0\)のとき1,\(D < 0\)のとき0ですから,解答は次のようになります。
共有点の個数は,\(a < \displaystyle\frac{17}{8}\)のとき2,\(a = \displaystyle\frac{17}{8}\)のとき1,\(a > \displaystyle\frac{17}{8}\)のとき0
