前回は三角比の方程式を解きましたが,今回は不等式に挑戦します。 単位円の定義を使いこなせるかどうかが試されます。
目次
三角比を含む不等式
前回,三角比を含む方程式を解けるようになりました。 不等式は,方程式が解けるなら難しくありません。 例として,次の不等式を解いてみましょう。 \(0^{\circ} \leqq \theta \leqq 180^{\circ}\)とします。
まずやるべきことは,方程式の場合と同じで,使う三角比の種類を1つだけにすることです。 三角比の相互関係である\(\sin^2\theta + \cos^2\theta = 1\)を使えば,\(\sin\theta\)に統一できそうですね。
ここで,\(0^{\circ} \leqq \theta \leqq 180^{\circ}\)のとき\(0 \leqq \sin\theta \leqq 1\)であることに注意すると,この不等式が成り立つのは次の場合です。
あとは\(\sin\theta\)が\(\displaystyle\frac{1}{2}\)よりも大きくなる\(\theta\)の範囲を求めるだけです。 \(\sin\theta\)は単位円周上の\(y\)座標でしたから,単位円周上の\(y\)座標が\(\displaystyle\frac{1}{2}\)より大きくなる部分を考えると,下図のオレンジ部分が該当します。
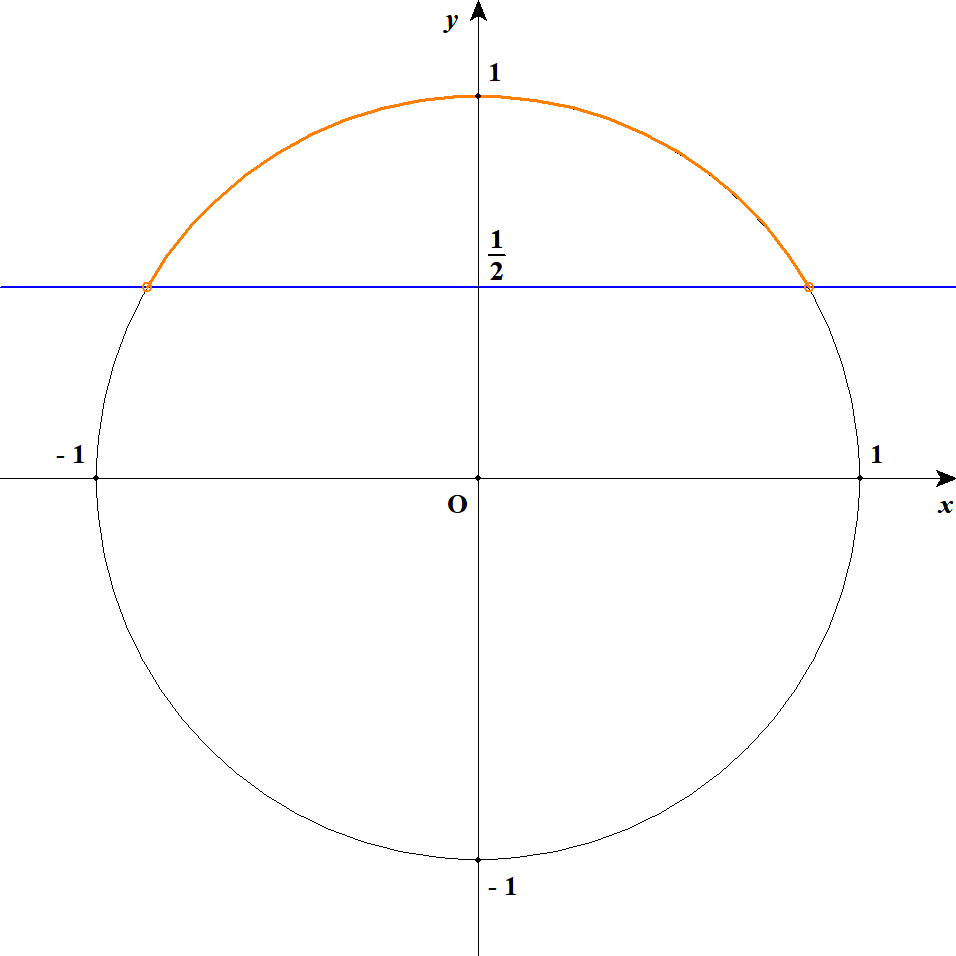
これに対応する\(\theta\)の範囲は,下図の赤い角度の部分になりますね。
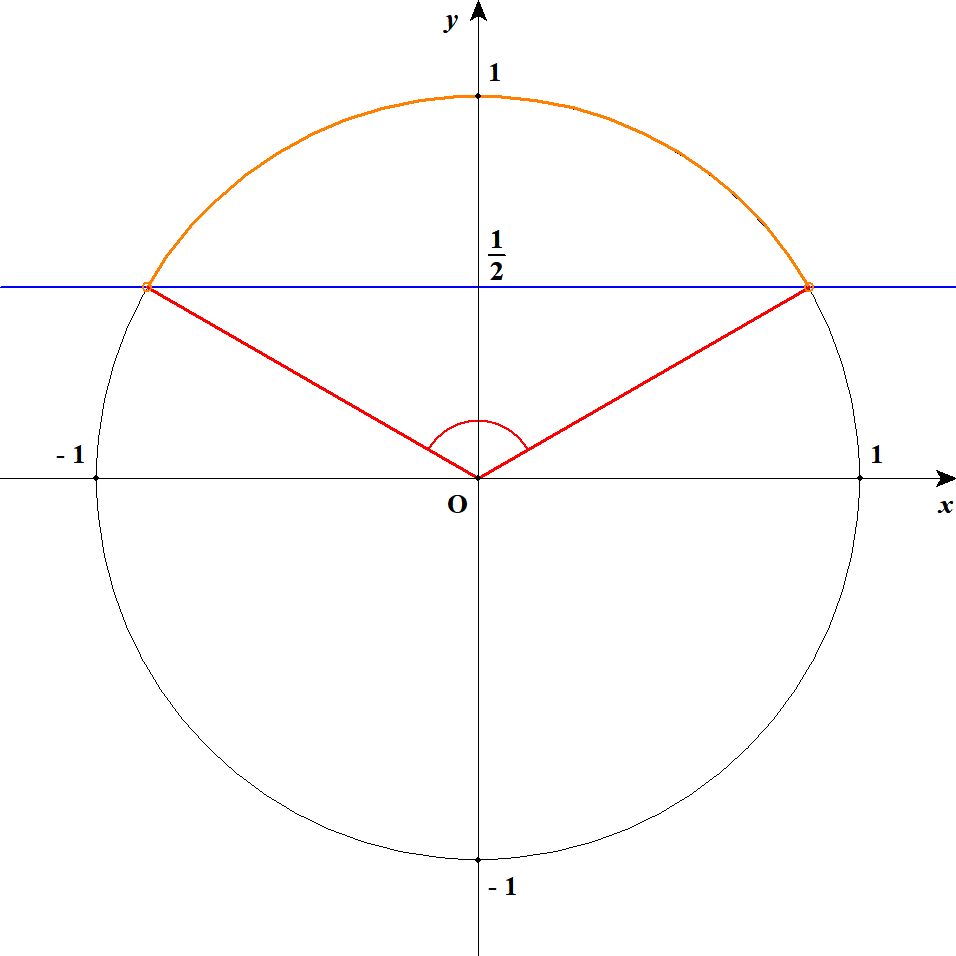
この\(\theta\)の範囲が不等式の解になります。 この範囲の端での\(\theta\)の値は,方程式\(\sin\theta = \displaystyle\frac{1}{2}\)を解けば分かります。 これを解くと,端の値が\(30^{\circ}, \ 150^{\circ}\)であることが分かりますから,不等式の解は\(30^{\circ} < \theta < 150^{\circ}\)です。
このように,三角比を含む不等式を解くときには,「\(\sin\theta\)は\(y\)座標,\(\cos\theta\)は\(x\)座標」というような認識が特に重要になってきます。 \(\sin\theta\)以外の三角比についての不等式も,確認問題で練習しておきましょう。
確認問題
次の不等式を解いてください。 ただし,\(0^{\circ} \leqq \theta \leqq 180^{\circ}\)とします。
-
\(\cos\theta \geqq -\displaystyle\frac{1}{2}\)
-
\(\sqrt{3}\tan\theta \geqq 1\)
-
\(2\sin\theta - \sqrt{3} < 0\)
-
\(\sin\theta \geqq 1\)
-
\(\cos\theta < 1\)
-
\(\tan\theta \leqq 1\)
答え
まずは単位円をかいて,条件を満たす\(\theta\)の範囲を図の中で考えます。 あとはその範囲の端での\(\theta\)の値を求めれば,不等式の解が分かります。
-
\(\cos\theta\)は単位円周上の\(x\)座標ですから,それが\(-\displaystyle\frac{1}{2}\)以上になるのは,下図のオレンジの範囲です。 それに対応する\(\theta\)の範囲は,図の赤い角度の部分ですね。
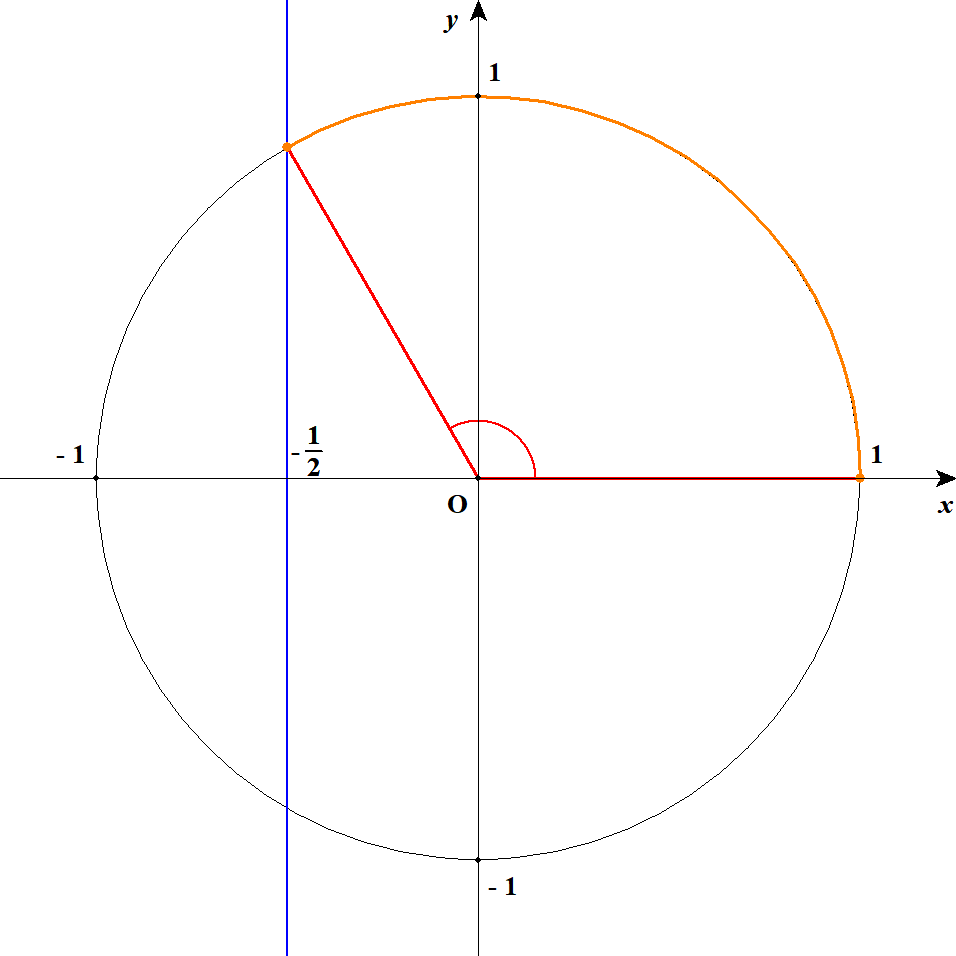
\(\cos\theta\)がちょうど\(-\displaystyle\frac{1}{2}\)になるのは,\(\theta = 120^{\circ}\)のときですから,これでこの不等式の解が\(0^{\circ} \leqq \theta \leqq 120^{\circ}\)であることが分かりました。
一応\(\cos\theta = -\displaystyle\frac{1}{2}\)となる\(\theta\)について,求め方を復習しておきます。 \(\cos\theta\)は単位円周上の\(x\)座標であり,これが負の値であることから,\(\theta\)は第2象限に来ていることが分かります。 つまり\(\theta\)は鈍角なのですが,考えづらいので,補角の公式を使って鋭角で考えます。 \(\cos\theta = \displaystyle\frac{1}{2}\)となる\(\theta\)は\(60^{\circ}\)ですね。 したがって,補角の公式より,\(\cos\theta = -\displaystyle\frac{1}{2}\)となる\(\theta\)が\(180^{\circ} - 60^{\circ} = 120^{\circ}\)と求まるわけです。
-
まず不等式を整理します。
\( \begin{align} \sqrt{3}\tan\theta &\geqq 1 \\[5pt] \tan\theta &\geqq \displaystyle\frac{1}{\sqrt{3}} \end{align} \)\(\tan\theta\)の定義はちょっと特殊でした。 原点と単位円周上の点を結ぶ線分を延長し,直線\(x = 1\)とぶつかる点の\(y\)座標を考えるんでしたね。 これが\(\displaystyle\frac{1}{\sqrt{3}}\)より大きくなるのは,下図のオレンジの範囲です。 それに対応する\(\theta\)は,図の赤い角度の部分ですね。
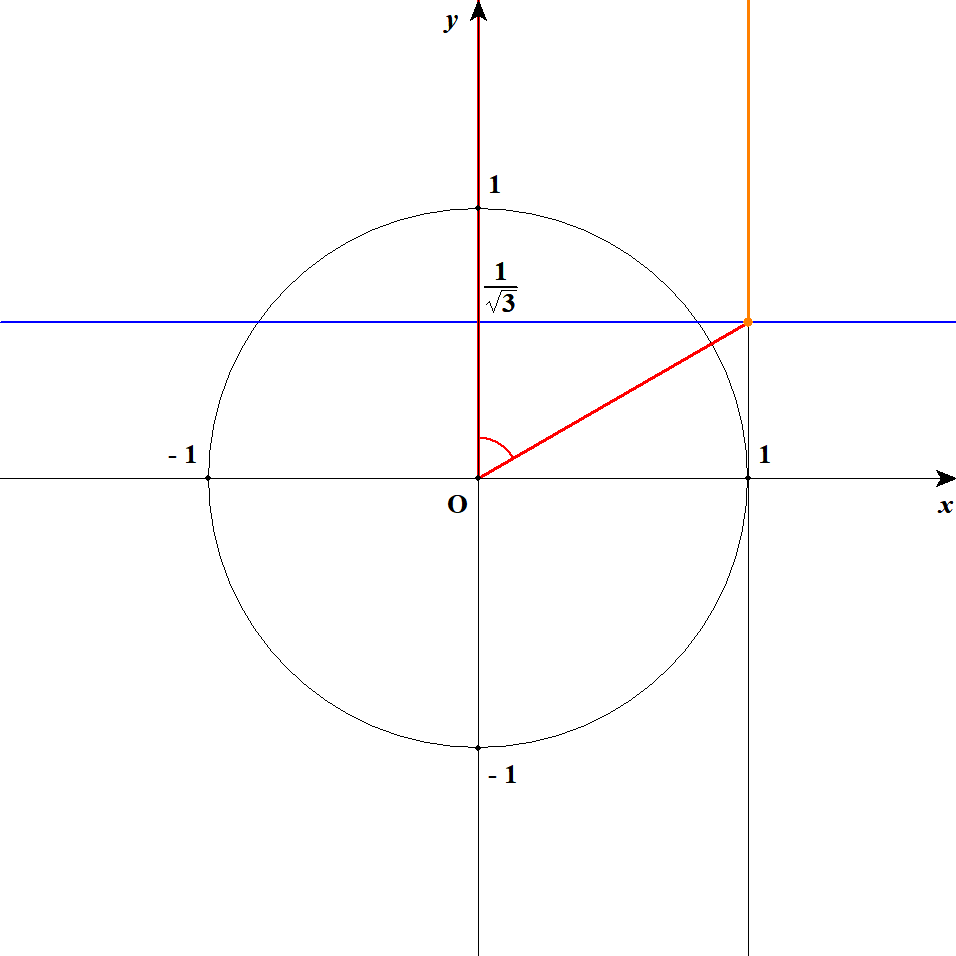
ただし,\(\tan90^{\circ}\)というものは存在しないということに注意してください。 \(\theta\)が第1象限から\(90^{\circ}\)に近づくのをイメージしてください。 近づくほど\(\tan\theta\)はどんどん大きくなりますね。 しかし,\(\theta\)が\(90^{\circ}\)になると,原点と円周上の点を結ぶ直線は,直線\(x = 1\)と平行になり,両者の交点はなくなります。 したがって,\(\tan90^{\circ}\)は定義できないため,不等式の解には含められません。
以上の点を踏まえつつ,今度はちょうど\(\tan\theta = \displaystyle\frac{1}{\sqrt{3}}\)となる\(\theta\)を考えると,\(\theta = 30^{\circ}\)です。 したがって,不等式の解は\(30^{\circ} \leqq \theta < 90^{\circ}\)となります。
-
まず不等式を整理します。
\( \begin{align} 2\sin\theta - \sqrt{3} &< 0 \\[5pt] 2\sin\theta &< \sqrt{3} \\[5pt] \sin\theta &< \displaystyle\frac{\sqrt{3}}{2} \end{align} \)\(\sin\theta\)は単位円周上の\(y\)座標ですから,それが\(\displaystyle\frac{\sqrt{3}}{2}\)未満になるのは,下図のオレンジの範囲です。 それに対応する\(\theta\)の範囲は,図の赤い角度の部分ですね。
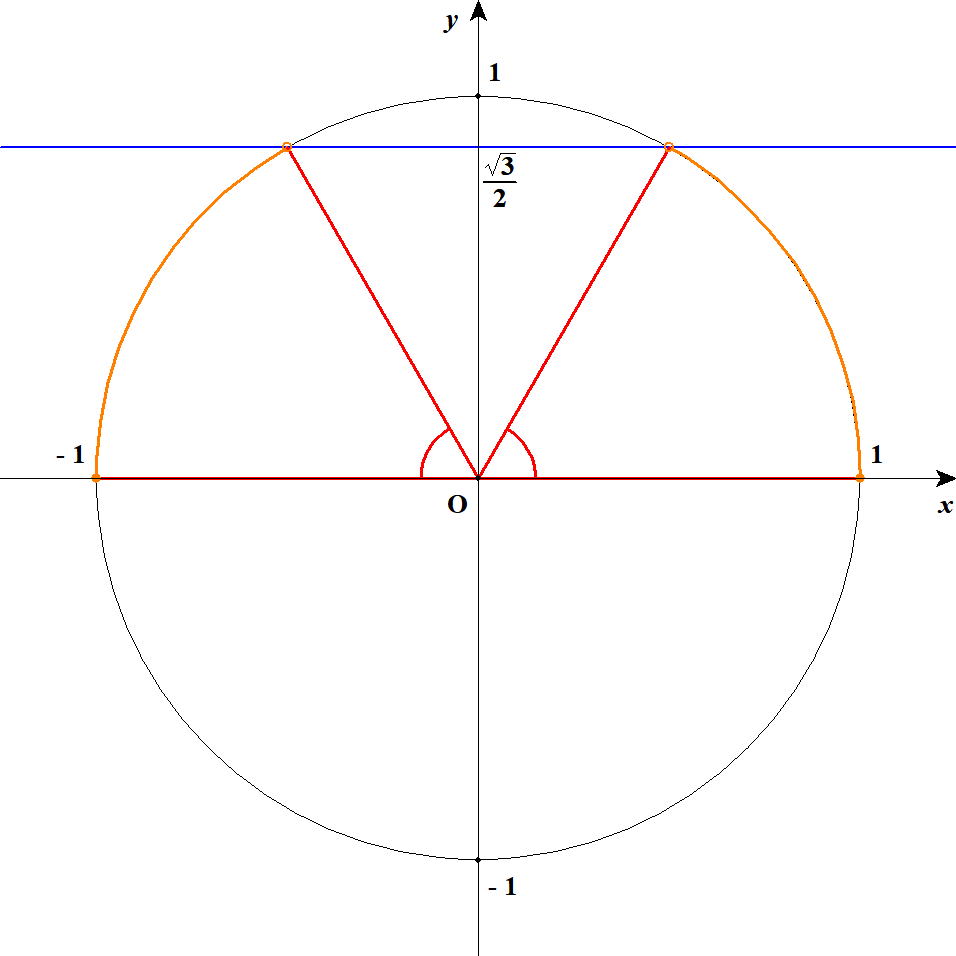
ちょうど\(\sin\theta = \displaystyle\frac{\sqrt{3}}{2}\)となる\(\theta\)は,\(\theta = 60^{\circ}, \ 120^{\circ}\)ですね。 鋭角の方は直角三角形をかけば分かりますし,鈍角の方は補角の公式で分かりますね。 したがって,不等式の解は,\(0^{\circ} \leqq \theta < 60^{\circ}\),\(120^{\circ} < \theta \leqq 180^{\circ}\)です。
-
\(\sin\theta\)は単位円周上の\(y\)座標ですから,\(0^{\circ} \leqq \theta \leqq 180^{\circ}\)のときは\(0 \leqq \sin\theta \leqq 1\)です。 よって,この値が\(1\)以上になるのは,\(\sin\theta = 1\)の場合しかありません。 このとき\(\theta = 90^{\circ}\)ですから,不等式の解は\(\theta = 90^{\circ}\)です。
-
\(\cos\theta\)は単位円周上の\(x\)座標ですから,\(-1 \leqq \cos\theta \leqq 1\)です。 よって,この値が\(1\)未満になるには,\(\cos\theta = 1\)でなければOKです。 \(\cos\theta = 1\)になるのは\(\theta = 0^{\circ}\)のときですから,不等式の解は\(0^{\circ} < \theta \leqq 180^{\circ}\)です。
-
\(\tan\theta\)は,原点と単位円周上の点を結ぶ線分を延長し,直線\(x = 1\)とぶつかる点の\(y\)座標です。 これが\(1\)以下になるのは,下図のオレンジの範囲です。 それに対応する\(\theta\)は,図の赤と緑の角度の部分ですね。
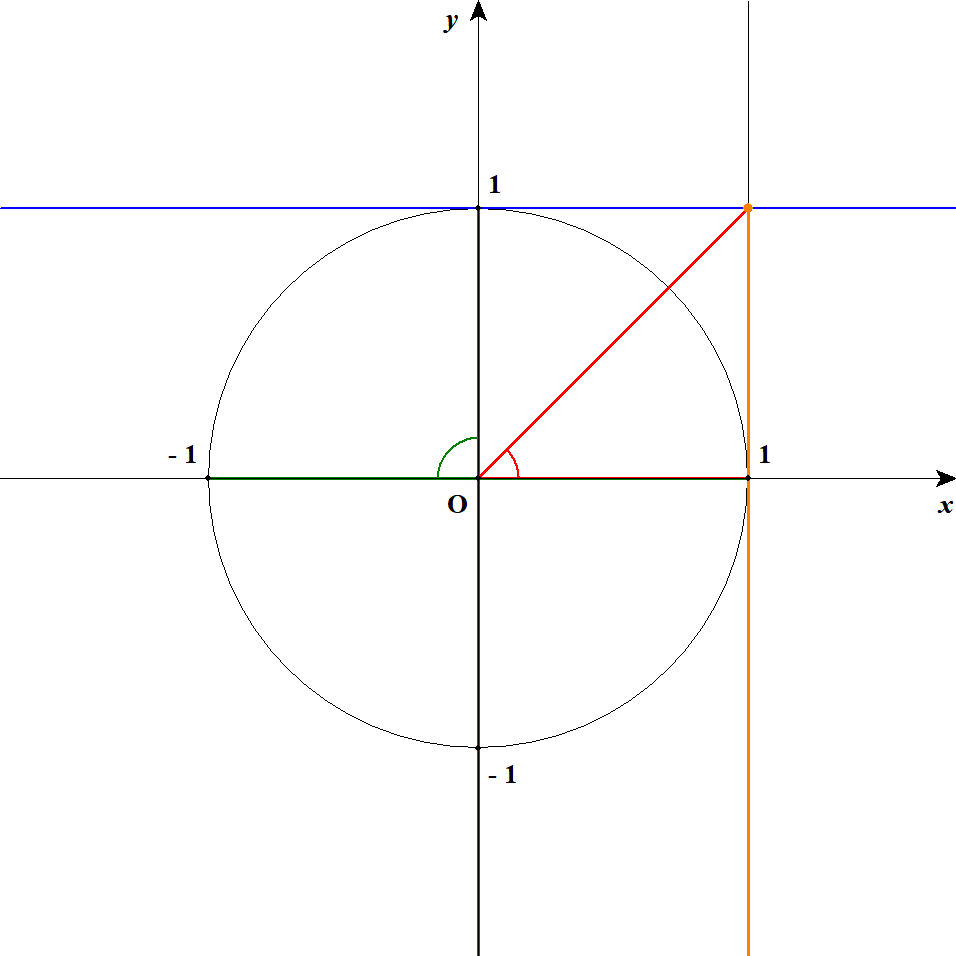
とはいわれても・・・図が見づらいです。 順番に確認して行きましょう。
第1象限の範囲(赤の部分)は問題ないと思います。 ちょうど\(\tan\theta = 1\)となるのは\(\theta = 45^{\circ}\)のときで,\(0^{\circ} \leqq \theta \leqq 45^{\circ}\)の範囲では\(\tan\theta \leqq 1\)が満たされます。 次に第2象限を考えると,このとき常に\(\tan \leqq 0\)であり,不等式が満たされます。 よって,\(90^{\circ} < \theta \leqq 180^{\circ}\)は不等式の解に含まれるわけです。 以上から,この不等式の解が\(0^{\circ} \leqq \theta \leqq 45^{\circ}\),\(90^{\circ} < \theta \leqq 180^{\circ}\)であることが分かりました。
次の不等式を解いてください。 ただし,(1),(2)では\(0^{\circ} \leqq \theta \leqq 180^{\circ}\)とし,(3)では\(0^{\circ} \leqq \theta < 90^{\circ}\)とします。
-
\(\sin\theta \leqq \cos\theta\)
-
\(4\sin^2\theta - 4\cos\theta < 5\)
-
\(4\sin\theta - \displaystyle\frac{1}{\cos\theta} + 2\tan\theta > 2\)
答え
三角比の相互関係を使って,不等式に登場する三角比の種類を1つだけにします。 不等式なので,両辺に何かを掛けたり,両辺を何かで割るときには符号に注意してください。 負の数をかけると,不等号の向きが変わるんでしたね。
-
次の相互関係の式を使います。
\( \begin{align} \tan\theta = \displaystyle\frac{\sin\theta}{\cos\theta} \end{align} \)不等式の両辺を\(\cos\theta\)で割れば,この相互関係の式により\(\tan\theta\)だけの不等式にできますね。 しかし\(0\)では割れないことや,負の数で割ると不等式の向きが変わることに注意が必要です。
[1] まず\(\cos\theta = 0\)の場合を考えます。 このとき不等式の両辺を\(\cos\theta\)で割ることはできませんから,不等式が成り立つか個別に確かめる必要があります。 このとき\(\theta = 90^{\circ}\)ですから,\(\sin\theta = 1\)であり,不等式は成り立ちません。 したがって,\(\theta = 90^{\circ}\)は不等式の解に含まれません。
[2] 次に\(\cos\theta > 0\)の場合を考えます。 このとき,\(0^{\circ} \leqq \theta < 90^{\circ}\)ですね。 不等式の両辺を\(\cos\theta\)で割ると,次のようになります。
\( \begin{align} \sin\theta &\leqq \cos\theta \\[5pt] \displaystyle\frac{\sin\theta}{\cos\theta} &\leqq 1 \\[5pt] \tan\theta &\leqq 1 \end{align} \)\(0^{\circ} \leqq \theta < 90^{\circ}\)であることを考慮すると,不等式を満たすのは\(0^{\circ} \leqq \theta \leqq 45^{\circ}\)のときだけですね。
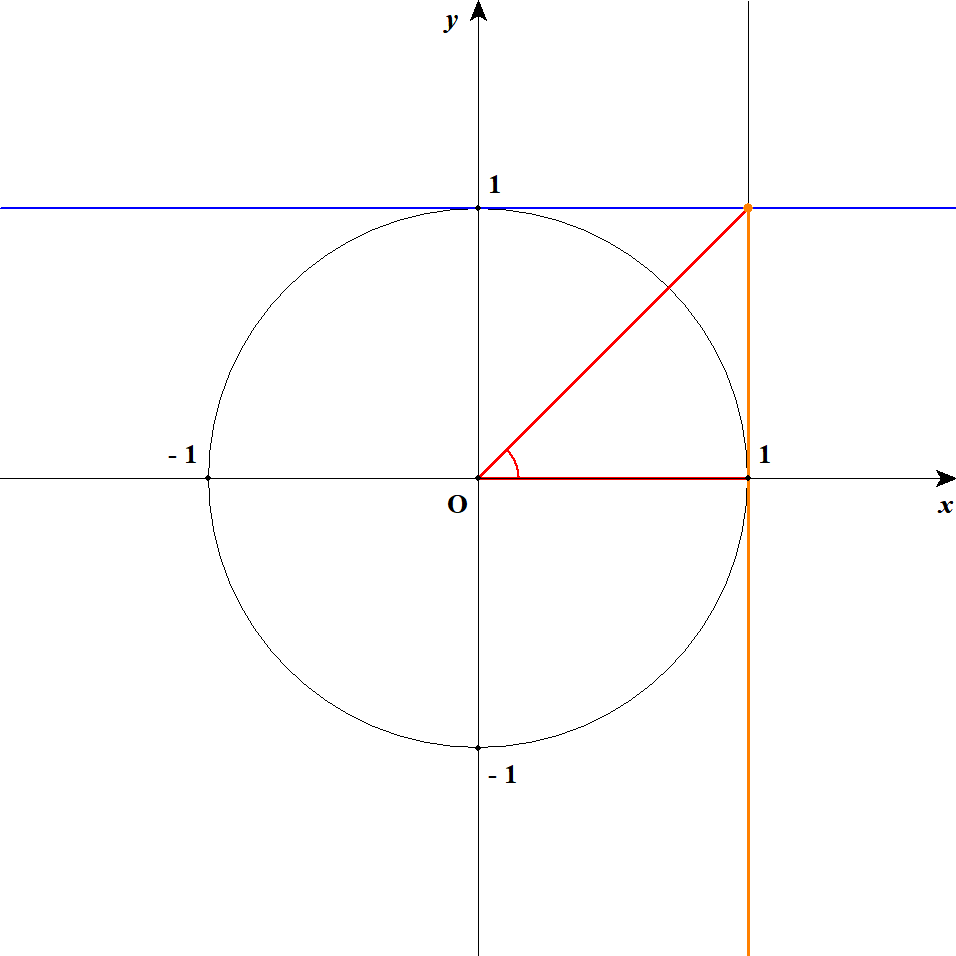
[3] 最後に\(\cos\theta < 0\)の場合を考えます。 このとき,\(90^{\circ} < \theta \leqq 180^{\circ}\)ですね。 不等式の両辺を\(\cos\theta\)で割ると,不等号の向きが変わって次のようになります。
\( \begin{align} \sin\theta &\leqq \cos\theta \\[5pt] \displaystyle\frac{\sin\theta}{\cos\theta} &\geqq 1 \\[5pt] \tan\theta &\geqq 1 \end{align} \)しかし,\(90^{\circ} < \theta \leqq 180^{\circ}\)であることを考慮すると,\(\tan\theta \leqq 0\)であるはずですから,不等式を満たす\(\theta\)は存在しません。
以上から,この不等式の解は\(0^{\circ} \leqq \theta \leqq 45^{\circ}\)です。
-
次の相互関係の式を使います。
\( \begin{align} \sin^2\theta + \cos^2\theta = 1 \end{align} \)これを使えば,\(\sin^2\theta\)を\(\cos^2\theta\)で表し,不等式を\(\cos\theta\)で統一することができます。
\( \begin{align} 4\sin^2\theta - 4\cos\theta &< 5 \\[5pt] 4(1 - \cos^2\theta) - 4\cos\theta &< 5 \\[5pt] 4 - 4\cos^2\theta - 4\cos\theta &< 5 \\[5pt] 4\cos^2\theta + 4\cos\theta + 1 &> 0 \\[5pt] (2\cos\theta + 1)^2 &> 0 \end{align} \)どんな実数でも2乗すれば\(0\)以上にはなりますから,不等式は\(2\cos\theta + 1 \neq 0\)でさえあれば成り立ちます。 \(2\cos\theta + 1 = 0\),すなわち\(\cos\theta = -\displaystyle\frac{1}{2}\)となるのは\(\theta = 120^{\circ}\)のときです。 したがって,この不等式の解は\(0^{\circ} \leqq \theta < 120^{\circ}\),\(120^{\circ} < \theta \leqq 180^{\circ}\)です。
-
不等式には三角比が3種類も登場しますから,まずは\(\tan\theta = \displaystyle\frac{\sin\theta}{\cos\theta}\)を使って\(\tan\theta\)を消しましょう。
\( \begin{align} 4\sin\theta - \displaystyle\frac{1}{\cos\theta} + 2\tan\theta &> 2 \\[5pt] 4\sin\theta - \displaystyle\frac{1}{\cos\theta} + 2\displaystyle\frac{\sin\theta}{\cos\theta} &> 2 \end{align} \)分母に\(\cos\theta\)があるので両辺に\(\cos\theta\)を掛けます。 \(0^{\circ} \leqq \theta < 90^{\circ}\)という条件から,\(\cos\theta > 0\)ですから,不等号の向きは変わりません。
\( \begin{align} 4\sin\theta - \displaystyle\frac{1}{\cos\theta} + 2\displaystyle\frac{\sin\theta}{\cos\theta} &> 2 \\[5pt] 4\sin\theta\cos\theta - 1 + 2\sin\theta &> 2\cos\theta \\[5pt] 4\sin\theta\cos\theta + 2\sin\theta - 2\cos\theta - 1 &> 0 \\[5pt] 2\sin\theta(2\cos\theta + 1) - (2\cos\theta + 1) &> 0 \\[5pt] (2\sin\theta - 1)(2\cos\theta + 1) &> 0 \end{align} \)\(\cos\theta > 0\)ですから,\(2\cos\theta + 1 > 0\)です。 したがって,この不等式が成り立つのは次の場合です。
\( \begin{align} 2\sin\theta - 1 &> 0 \\[5pt] \sin\theta > \displaystyle\frac{1}{2} \end{align} \)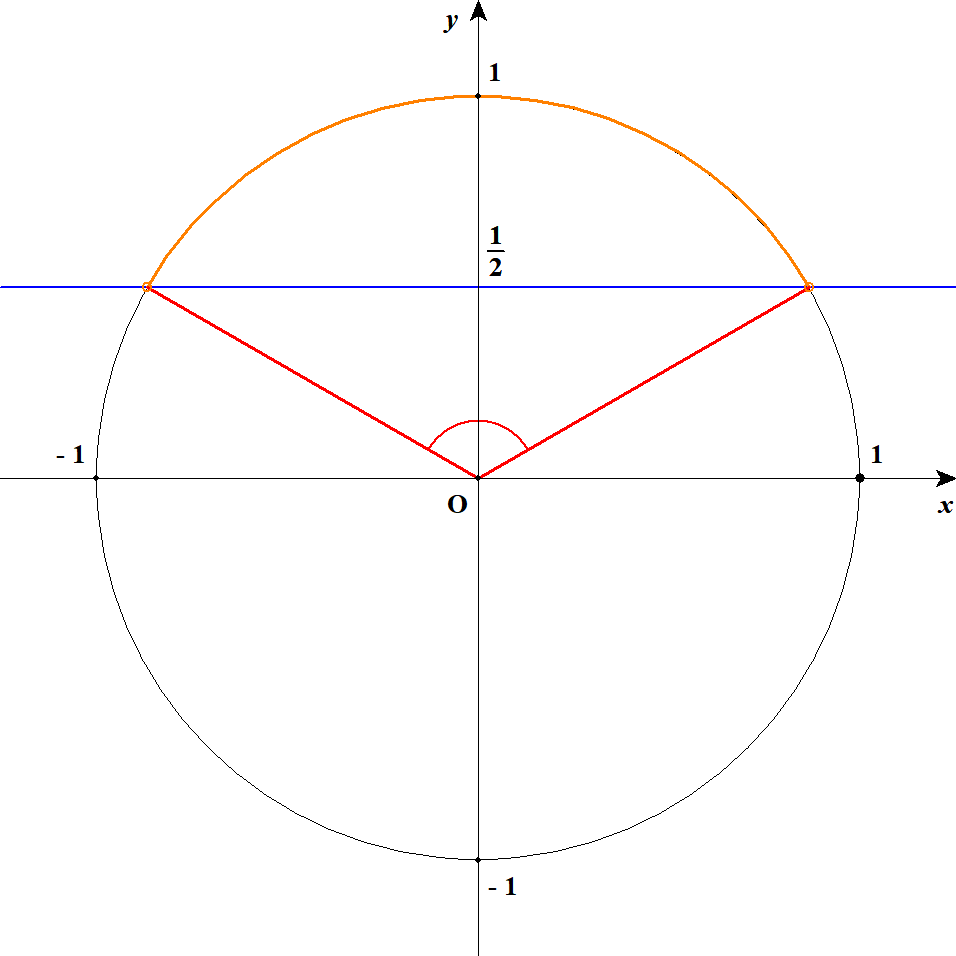
図を見るとこの不等式は\(30^{\circ} < \theta < 150^{\circ}\)で成り立つことが分かりますが,この問題には\(0^{\circ} \leqq \theta < 90^{\circ}\)という条件があります。 したがって,この不等式の解は\(30^{\circ} < \theta < 90^{\circ}\)です。
次の不等式を解いてください。 ただし,\(0^{\circ} \leqq \theta \leqq 180^{\circ}\)とします。
答え
実は前問を解く過程で出てくる不等式なのですが,\(\theta\)の範囲を広げています。 2つの式の積が正になるのは,因数が同符号のときです。 因数が両方とも正の場合と,両方とも負の場合に分けて考えましょう。
[1] まず因数が両方とも正の場合を考えます。 次の連立不等式を解けば良いですね。
ひとつめの不等式を整理すると\(\sin\theta > \displaystyle\frac{1}{2}\)であり,これを解くと\(30^{\circ} < \theta < 150^{\circ}\)です。

ふたつめの不等式を整理すると\(\cos\theta > -\displaystyle\frac{1}{2}\)であり,これを解くと\(0^{\circ} \leqq \theta < 120^{\circ}\)です。
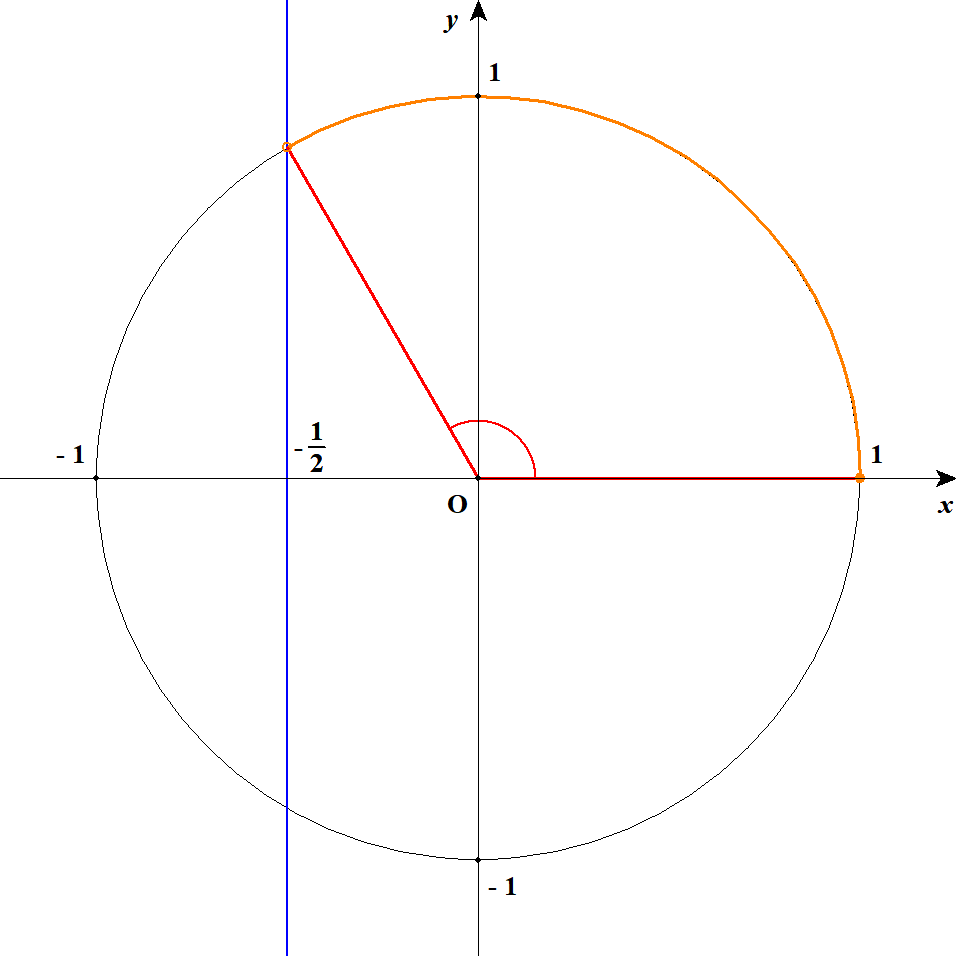
\(\theta\)の共通範囲をとると,この連立不等式の解が\(30^{\circ} < \theta < 120^{\circ}\)であると分かります。
[2] 次に因数が両方とも負の場合を考えます。 次の連立不等式を解けば良いですね。
ひとつめの不等式を整理すると\(\sin\theta < \displaystyle\frac{1}{2}\)であり,これを解くと\(0^{\circ} \leqq \theta < 30^{\circ}\),\(150^{\circ} < \theta \leqq 180^{\circ}\)です。
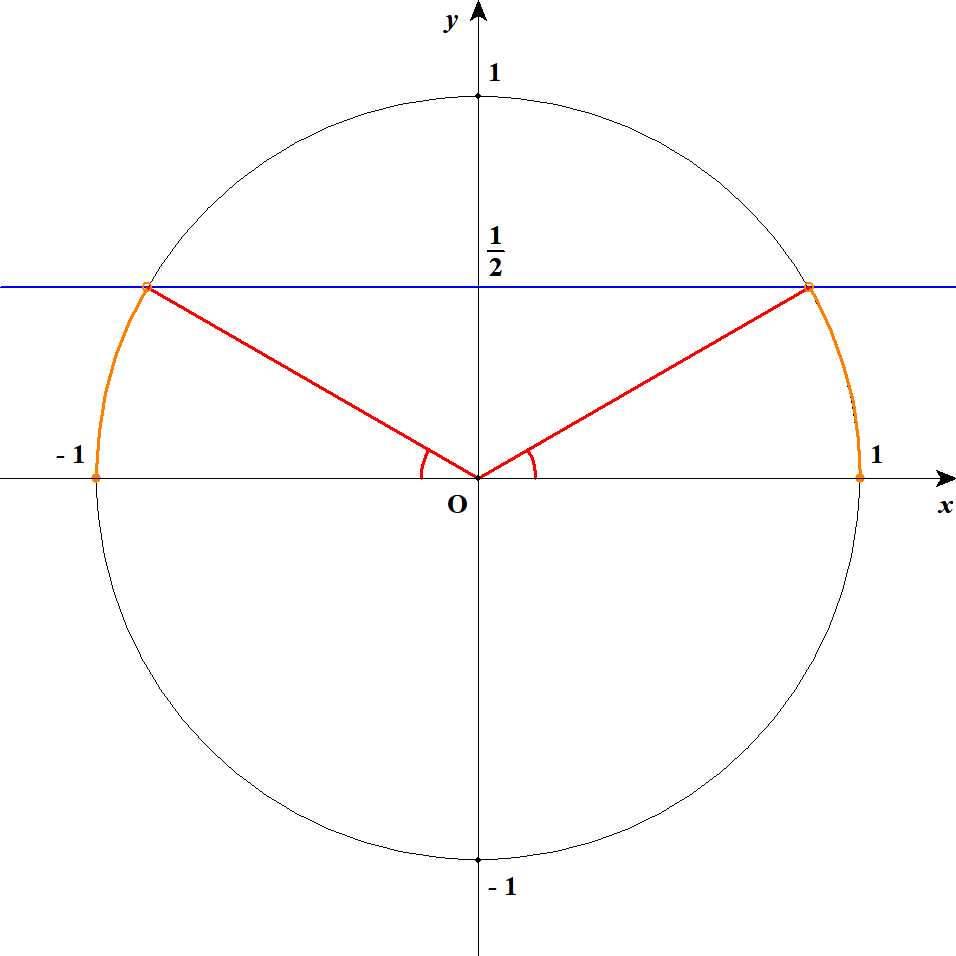
ふたつめの不等式を整理すると\(\cos\theta < -\displaystyle\frac{1}{2}\)であり,これを解くと\(120^{\circ} < \theta \leqq 180^{\circ}\)です。
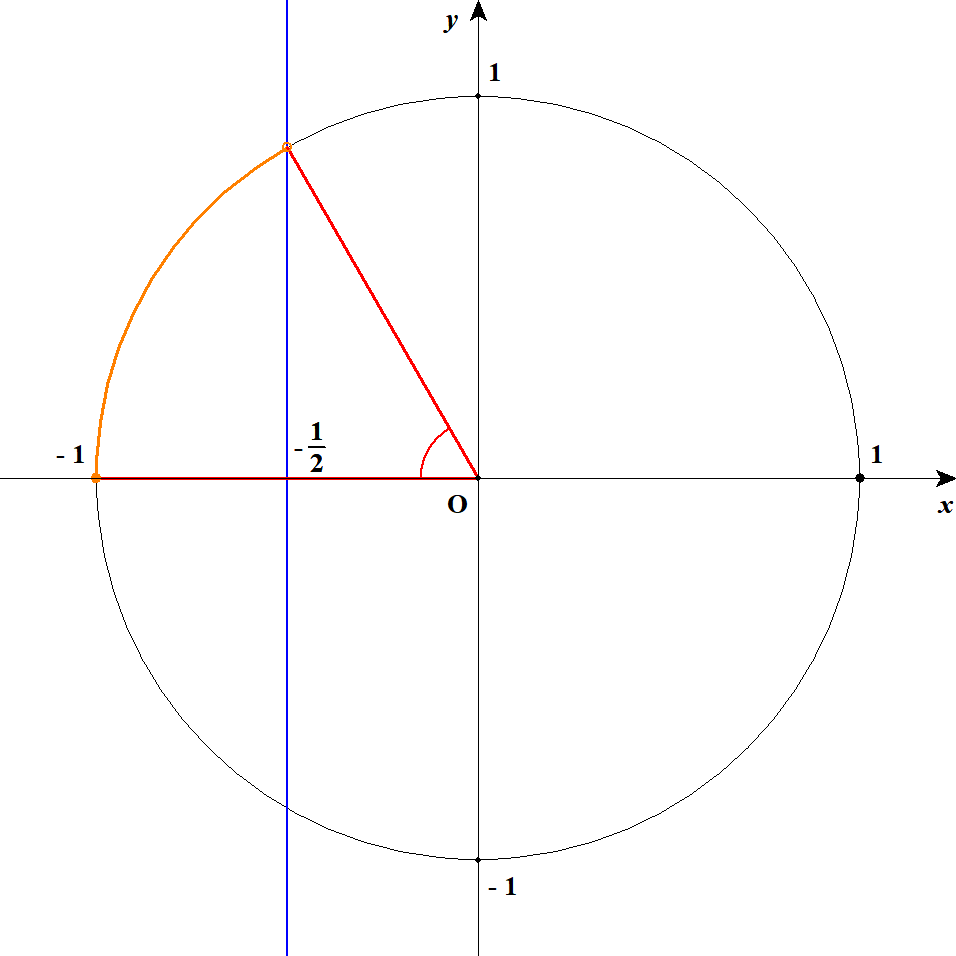
\(\theta\)の共通範囲をとると,この連立不等式の解が\(150^{\circ} < \theta \leqq 180^{\circ}\)であると分かります。
[1], [2]より,この不等式の解は\(30^{\circ} < \theta < 120^{\circ}\),\(150^{\circ} < \theta \leqq 180^{\circ}\)です。
