今回は三角比の方程式を解きます。 ある状況を満たす角度を求めるためには,このような方程式を解ける必要があります。
目次
三角比を含む方程式
三角比がいつどんな値をとるかを理解していれば,逆算で方程式を解くことができます。 例として1つ方程式を解いてみましょう。 \(0^{\circ} \leqq \theta \leqq 180^{\circ}\)とします。
この方程式を満たす\(\theta\)をそのまま求めようとしても難しいと思います。 \(\sin\theta\)と\(\cos\theta\)の値の変動の仕方は違うため,同時に考えづらいからです。
同時に考えられないならどうすれば良いか? 三角比の相互関係を使って,\(\sin\theta\),\(\cos\theta\),\(\tan\theta\)のどれかに統一してしまえば良いのです。 この場合は\(\sin^2\theta + \cos^2\theta = 1\)を使って,\(\sin\theta\)に統一するのが良いでしょう。
使う三角比を統一したら\(\sin\theta\)の2次方程式になりましたね。 因数分解して解いてみましょう。
これで方程式を満たす\(\sin\theta\)の値が分かりました。 しかしここで終わってはいけません。 \(\sin\theta\)がその値になる\(\theta\)の値を求める必要があります。
まず\(\sin\theta = -2\)についてですが,これを満たす\(\theta\)は存在しません。 単位円の定義を思い出してください。 \(\sin\theta\)は単位円周上の点の\(y\)座標ですから,\(0^{\circ} \leqq \theta \leqq 180^{\circ}\)のとき\(0 \leqq \sin\theta \leqq 1\)だからです。
次に\(\sin\theta = \displaystyle\frac{1}{2}\)について考えます。 まず単位円の図をかいてみます。
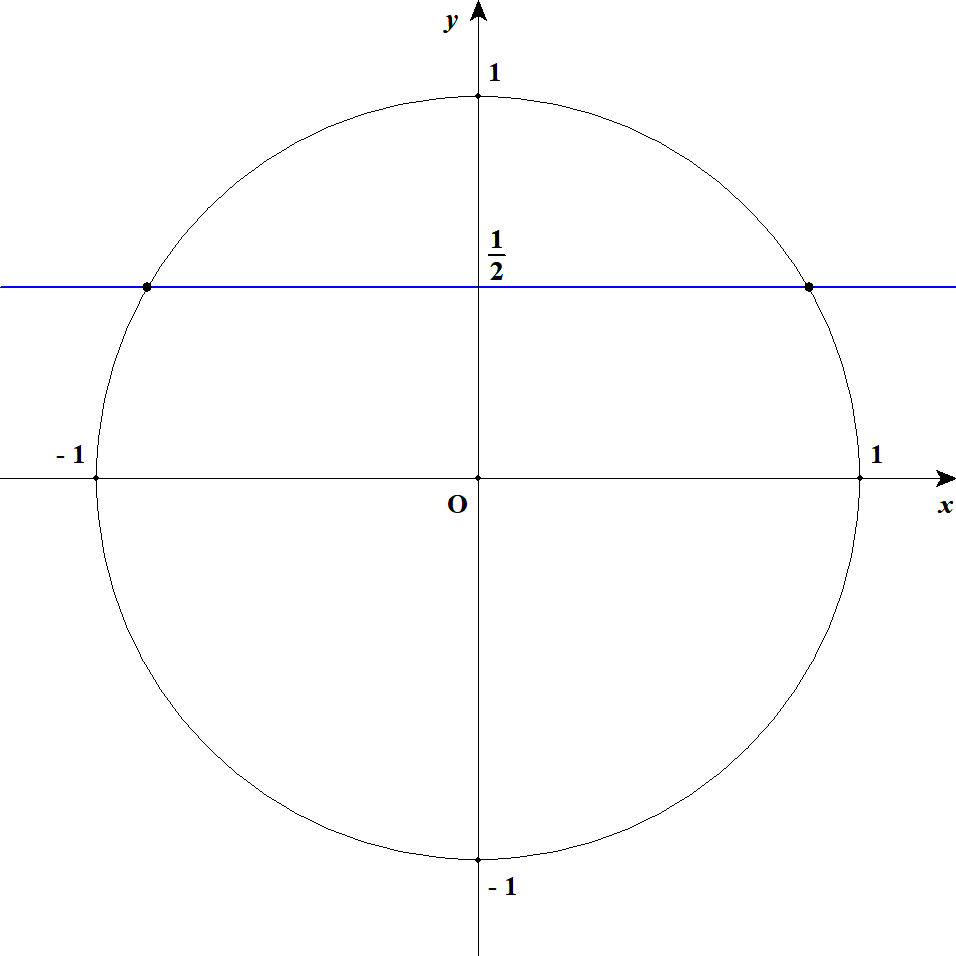
\(\sin\theta\)は\(y\)座標ですから,図には青色で直線\(y = \displaystyle\frac{1}{2}\)をかいています。 単位円と直線の交点は2つありますから,求める\(\theta\)は2つあるようです。 つまり,下図の赤の角度と緑の角度を求める必要があります。
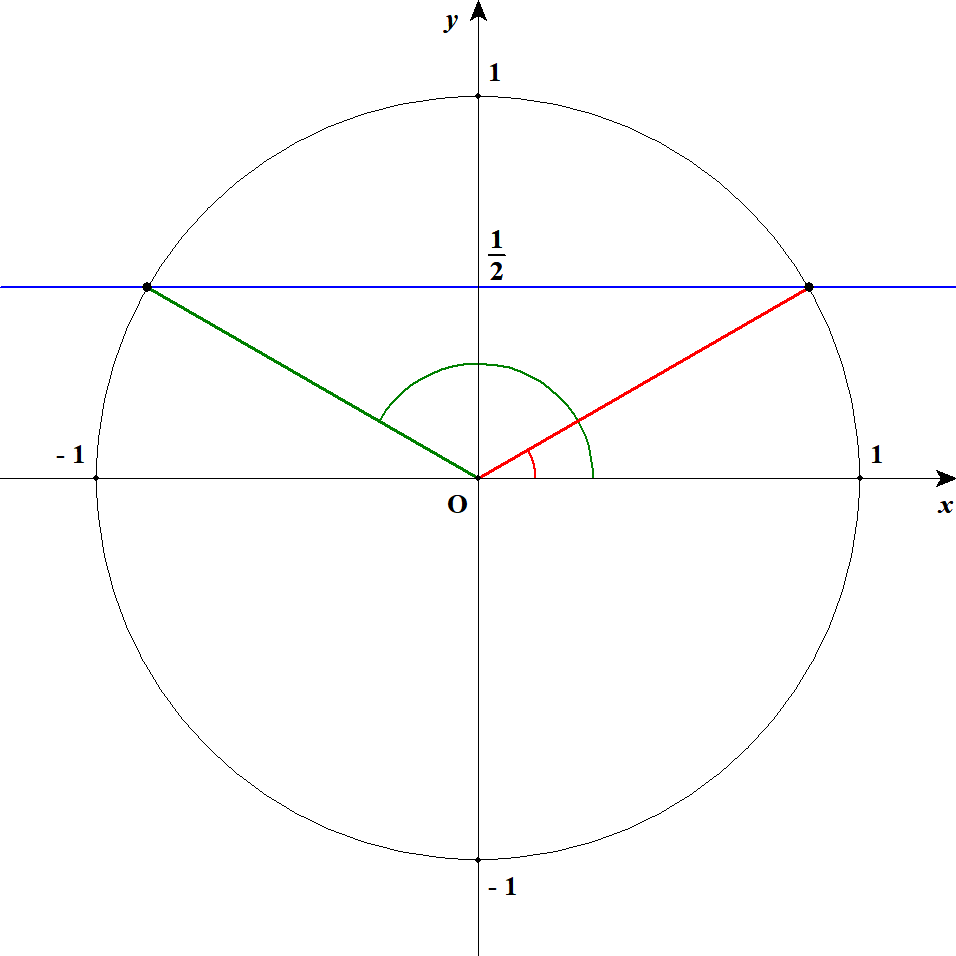
この角度を求めるには,直角三角形で考えた方が分かりやすいです。 \(\sin\theta\)が\(\displaystyle\frac{1}{2}\)になるのは次の直角三角形ですね。
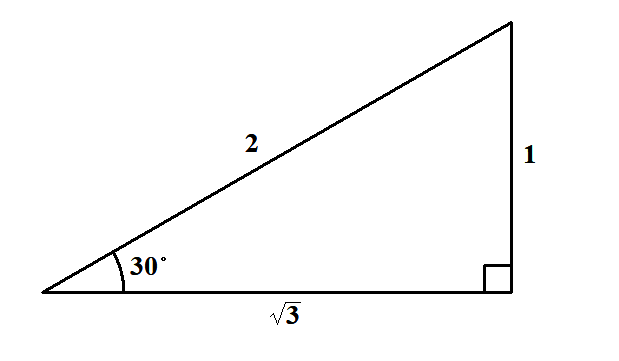
というわけで,赤い角度の方は\(30^{\circ}\)です。 緑の方は,補角の公式により\(150^{\circ}\)であると分かります。 これでこの方程式の解が\(\theta = 30^{\circ}, \ 150^{\circ}\)であることが分かりました。
\(\theta\)の候補としては,基本的には\(30^{\circ}\),\(45^{\circ}\),\(60^{\circ}\)とその補角,あとは\(0^{\circ}\),\(90^{\circ}\),\(180^{\circ}\)くらいしかありません。 これらの値は判断できるようにしておきましょう。
方程式を解くときには,どこかに\(\theta = 30^{\circ}\),\(45^{\circ}\),\(60^{\circ}\)の直角三角形をかいておいて,すぐに見れるようにしておくことをオススメします。
三角比の値から\(\theta\)を逆算するのは,慣れてしまえば簡単です。 まず補角の公式のおかげで,\(\theta\)として鋭角のものさえ求められれば,他の値も分かります。 本文で見た例もそうでしたね。
数学Ⅰでは,鋭角の中でも基本的に\(30^{\circ}\),\(45^{\circ}\),\(60^{\circ}\)しか登場しません。 問題は,どうやって三角比の値から\(\theta\)の値を判断するかです。
もっとも基本的な方法は,直角三角形をかいてみて,どの角度が当てはまるのかを考えることです。 以下で他の方法も見てみましょう。
\(\theta\)が鋭角のとき,\(\theta\)が大きくなるにつれて,\(\sin\theta\),\(\tan\theta\)は大きくなり,\(\cos\theta\)は小さくなっていきます。 これを\(\sin\theta\),\(\tan\theta\)は単調増加し,\(\cos\theta\)は単調減少するといいます。 実際にそうなることは,単位円の定義を思い出せば分かります。
これは\(\theta\)の判別に有用な情報です。 三角比がよくとる値さえ頭に入っていれば,簡単に\(\theta\)が判別できることを次の例で確認してみてください。
【例】\(\cos\theta\ = \displaystyle\frac{\sqrt{3}}{2}\)となる\(\theta\)が\(30^{\circ}\),\(45^{\circ}\),\(60^{\circ}\)のどれなのか考えましょう。 \(\cos\theta\)の値は\(\displaystyle\frac{1}{2}\),\(\displaystyle\frac{1}{\sqrt{2}}\),\(\displaystyle\frac{\sqrt{3}}{2}\)のどれかです。 \(\displaystyle\frac{\sqrt{3}}{2}\)はこの中で一番大きな値ですから,\(\cos\theta\)が単調減少することを考慮すると,最初に現れる値だと分かります。 ということは\(\theta = 30^{\circ}\)です。
確認問題
次の方程式を解いてください。 ただし,\(0^{\circ} \leqq \theta \leqq 180^{\circ}\)とします。
-
\(\cos\theta = -\displaystyle\frac{1}{2}\)
-
\(\sqrt{3}\tan\theta = 1\)
-
\(2\sin\theta - \sqrt{3} = 0\)
-
\(\sin\theta = 1\)
-
\(\cos\theta = 1\)
-
\(\tan\theta = 1\)
答え
三角比を含む方程式を解くには,直角三角形をかいて当てはまるものを探すのが基本です。
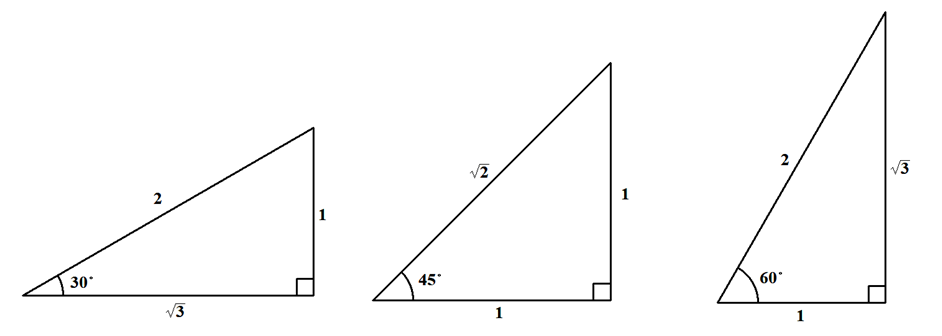
-
\(\cos\theta\)が\(-\displaystyle\frac{1}{2}\)になる状況は,下図の通りです。 直線\(x = -\displaystyle\frac{1}{2}\)を青線でかいています。 赤の角度を求めれば良いですね。
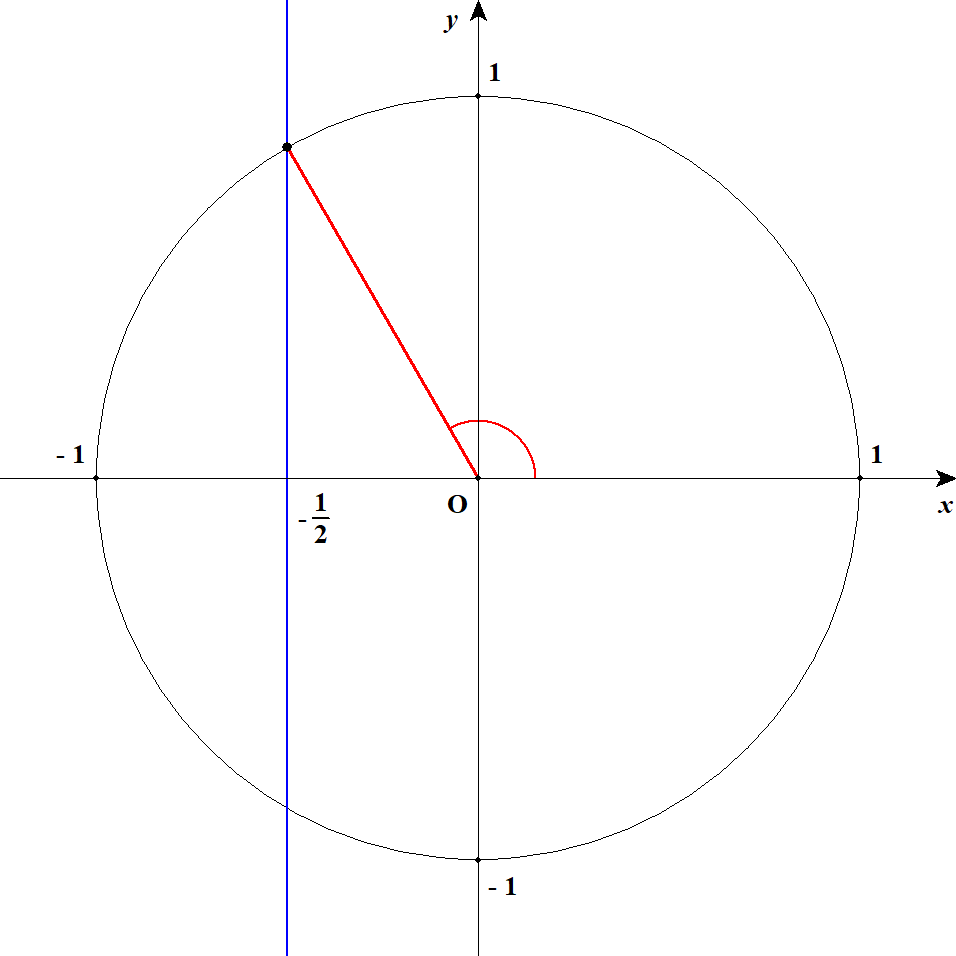
補角の公式を使うと,方程式を次のように変形できます。
\( \begin{align} \cos\theta &= -\displaystyle\frac{1}{2} \\[5pt] -\cos(180^{\circ} - \theta) &= -\displaystyle\frac{1}{2} \\[5pt] \cos(180^{\circ} - \theta) &= \displaystyle\frac{1}{2} \end{align} \)この式から,とりあえず\(\cos\phi\)が\(\displaystyle\frac{1}{2}\)となる鋭角の\(\phi\)を求めれば,\(\theta = 180^{\circ} - \phi\)と分かります。 直角三角形で確認すれば,\(\phi = 60^{\circ}\)であることが分かりますから,\(\theta = 180^{\circ} - 60^{\circ} = 120^{\circ}\)です。
-
まず方程式を整理します。
\( \begin{align} \sqrt{3}\tan\theta &= 1 \\[5pt] \tan\theta &= \displaystyle\frac{1}{\sqrt{3}} \end{align} \)\(\tan\theta\)が\(\displaystyle\frac{1}{\sqrt{3}}\)になる状況は,下図の通りです。 直線\(y = \displaystyle\frac{1}{\sqrt{3}}\)を青線でかいています。 赤の角度を求めれば良いですね。
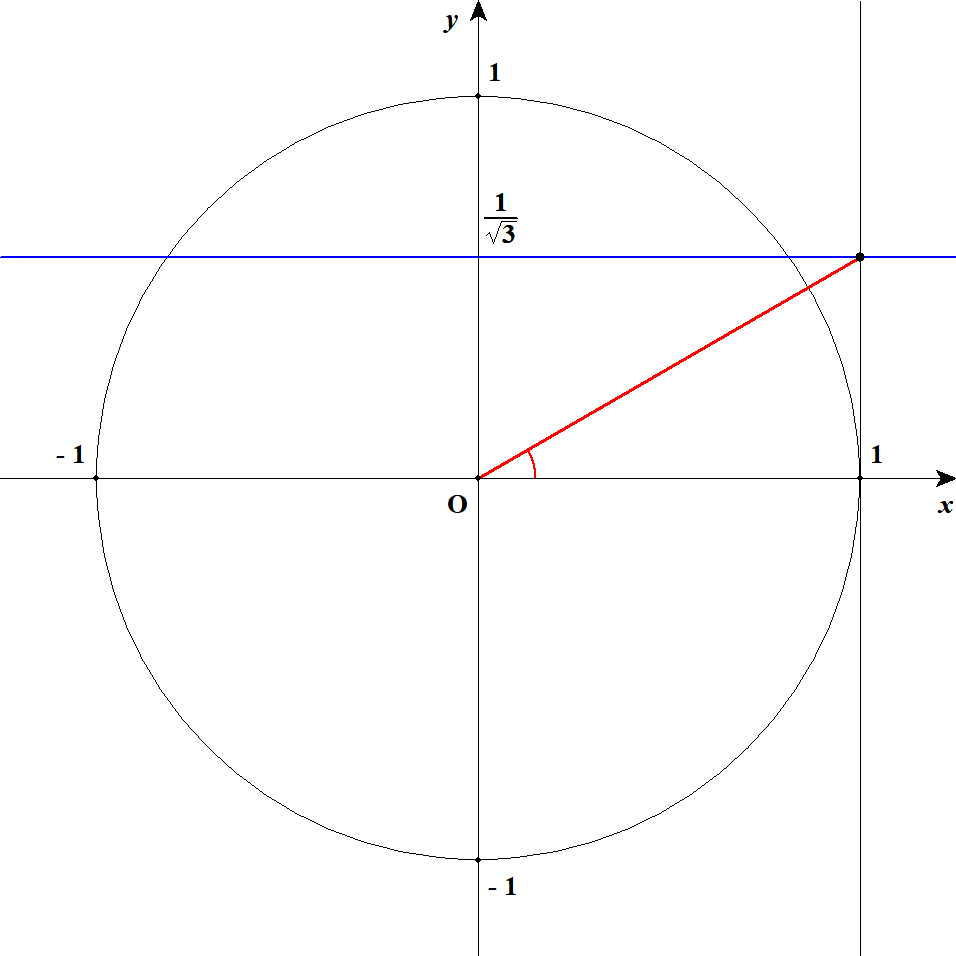
直角三角形で確認すれば,\(\theta = 30^{\circ}\)であることが分かります。
-
まず方程式を整理します。
\( \begin{align} 2\sin\theta - \sqrt{3} &= 0 \\[5pt] 2\sin\theta &= \sqrt{3} \\[5pt] \sin\theta &= \displaystyle\frac{\sqrt{3}}{2} \end{align} \)\(\sin\theta\)が\(\displaystyle\frac{\sqrt{3}}{2}\)になる状況は,下図の通りです。 直線\(y = \displaystyle\frac{\sqrt{3}}{2}\)を青線でかいています。 赤と緑の角度を求めれば良いですね。
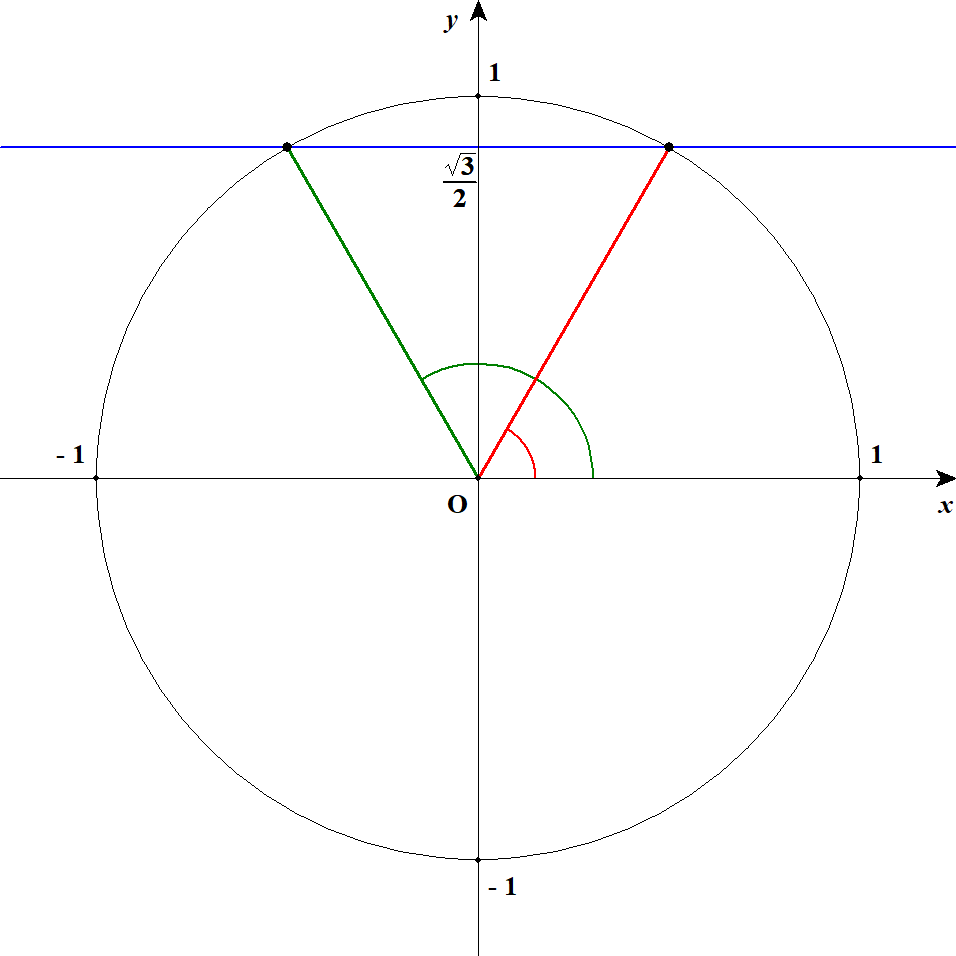
まずは鋭角である赤の角度を求めます。 直角三角形で確認すれば,\(\theta = 60^{\circ}\)であることが分かります。 同時に緑の角度についても,補角の公式から\(\theta = 180^{\circ} - 60^{\circ} = 120^{\circ}\)であると分かります。 したがって,\(\theta = 60^{\circ}, \ 120^{\circ}\)です。
-
\(\sin\theta\)は単位円周上の\(y\)座標です。 それが\(1\)になるのは,円の一番上の点だけですね。 したがって,\(\theta = 90^{\circ}\)であると分かります。
-
\(\cos\theta\)は単位円周上の\(x\)座標です。 それが\(1\)になるのは,円の一番右の点だけですね。 したがって,\(\theta = 0^{\circ}\)であると分かります。
-
\(\tan\theta\)が\(1\)になる状況は,下図の通りです。 直線\(y = 1\)を青線でかいています。 赤の角度を求めれば良いですね。
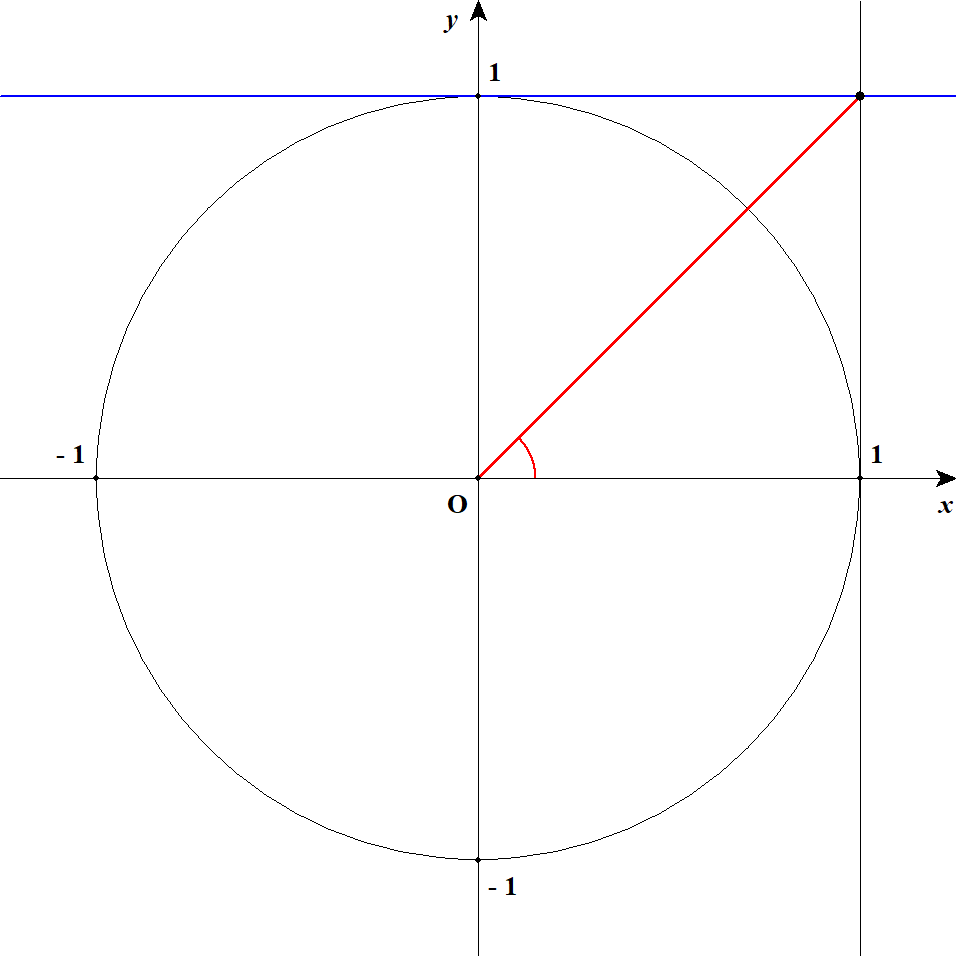
直角三角形で確認すれば,\(\theta = 45^{\circ}\)であることが分かります。
次の方程式を解いてください。 ただし,\(0^{\circ} \leqq \theta \leqq 180^{\circ}\)とします。
-
\(\sin\theta = \cos\theta\)
-
\(4\sin^2\theta - 4\cos\theta = 5\)
-
\(4\sin\theta - \displaystyle\frac{1}{\cos\theta} + 2\tan\theta = 2\)
答え
同時に複数種類の三角比を扱うのは難しいです。 三角比の相互関係を使って,方程式を\(\sin\theta\),\(\cos\theta\),\(\tan\theta\)のどれかひとつだけで表すようにしましょう。 相互関係の式は次の3つでしたね。
-
\(\sin\theta\)と\(\cos\theta\)の2つを使う相互関係の式を見てみましょう。 平方の形がないことを考慮すると,使えそうな関係式は2つめのものです。 方程式の両辺を\(\cos\theta\)で割れば,\(\tan\theta\)だけの方程式にできますね。
ただし,割り算をするときには注意すべきことがあります。 \(0\)で割ってはならないということです。 \(\cos\theta = 0\)となる場合は別で考える必要があります。 \(\cos\theta\)が\(0\)となるのは,\(\theta = 90^{\circ}\)のときですが,このとき\(\sin\theta = 1\)ですから,方程式は成り立たず,この\(\theta\)は解になりません。
次に\(\theta \neq 90^{\circ}\)の場合を考えましょう。 このときは\(\cos\theta \neq 0\)ですから,両辺を\(\cos\theta\)で割っても問題ありません。
\( \begin{align} \sin\theta &= \cos\theta \\[5pt] \displaystyle\frac{\sin\theta}{\cos\theta} &= 1 \\[5pt] \tan\theta &= 1 \end{align} \)ここまで変形できたら,あとは\(\tan\theta\)が\(1\)となる\(\theta\)を探すだけですね。 直角三角形で確認すれば,解が\(\theta = 45^{\circ}\)であることが分かります。
-
方程式には\(\sin\theta\)と\(\cos\theta\)が登場します。 \(\sin\theta\)が平方の形であることを考慮すると,相互関係の式の1つめが使えそうですね。
\( \begin{align} 4\sin^2\theta - 4\cos\theta &= 5 \\[5pt] 4(1 - \cos^2\theta) - 4\cos\theta &= 5 \\[5pt] 4 - 4\cos^2\theta - 4\cos\theta &= 5 \\[5pt] 4\cos^2\theta + 4\cos\theta + 1 &= 0 \\[5pt] (2\cos\theta + 1)^2 &= 0 \\[5pt] \cos\theta &= -\displaystyle\frac{1}{2} \end{align} \)ここまで変形できたら,あとは\(\cos\theta\)が\(-\displaystyle\frac{1}{2}\)となる\(\theta\)を探すだけですね。 まず\(\cos\phi = \displaystyle\frac{1}{2}\)となる\(\phi\)を探すと,直角三角形で確認すれば,\(\phi = 60^{\circ}\)だとわかります。 したがって,補角の公式より,解が\(\theta = 120^{\circ}\)であることが分かります。
-
方程式には3種類の三角比が登場します。 まずは2種類に減らしてみましょう。 相互関係の式の2つめを使えば,\(\tan\theta\)はなくすことができそうです。 分母に\(\cos\theta\)があることと,\(\tan\theta\)があることから,\(\cos\theta \neq 0\)であり,\(\theta \neq 90^{\circ}\)であることに注意です。
\( \begin{align} 4\sin\theta - \displaystyle\frac{1}{\cos\theta} + 2\tan\theta &= 2 \\[5pt] 4\sin\theta - \displaystyle\frac{1}{\cos\theta} + 2\displaystyle\frac{\sin\theta}{\cos\theta} &= 2 \\[5pt] 4\sin\theta\cos\theta - 1 + 2\sin\theta &= 2\cos\theta \\[5pt] 4\sin\theta\cos\theta + 2\sin\theta - 2\cos\theta - 1 &= 0 \end{align} \)分かりにくいかもしれませんが,左辺は因数分解できます。 複数の文字を含む式を因数分解するときは,まずひとつの文字について式を整理すると良いんでしたね。 一見因数分解できなさそうな式でも,一度整理して確かめるべきですね。
\( \begin{align} 4\sin\theta\cos\theta + 2\sin\theta - 2\cos\theta - 1 &= 0 \\[5pt] 2\sin\theta(2\cos\theta + 1) - (2\cos\theta + 1) &= 0 \\[5pt] (2\sin\theta - 1)(2\cos\theta + 1) &= 0 \end{align} \)この方程式が満たされるのは,\(\sin\theta = \displaystyle\frac{1}{2}\)または\(\cos\theta = -\displaystyle\frac{1}{2}\)の場合です。 それぞれ解いていきましょう。 どちらの問題も,今回の本文や確認問題の中で既に解いたものですが,軽く確認しておきます。
まず\(\sin\theta = \displaystyle\frac{1}{2}\)となる\(\theta\)は2つあります。 \(\sin\theta\)は円周上の\(y\)座標なので,第1,第2象限の2つの点で\(\displaystyle\frac{1}{2}\)をとれるわけです。 そのうち鋭角の方は\(30^{\circ}\)で,鈍角の方は補角の公式から\(150^{\circ}\)だとわかります。
次に\(\cos\theta = -\displaystyle\frac{1}{2}\)となる\(\theta\)を考えます。 \(\cos\theta\)は円周上の\(x\)座標ですから,それが負になるのは鈍角の1つですね。 ただし鈍角だと考えづらいので,補角の公式を利用します。 そうすれば,まず\(\cos\theta = \displaystyle\frac{1}{2}\)となる鋭角を考えればよく,それは\(60^{\circ}\)です。 したがって,補角の公式より,\(\cos\theta = -\displaystyle\frac{1}{2}\)となる\(\theta\)は\(120^{\circ}\)です。
以上から,方程式の解は\(\theta = 30^{\circ}, \ 120^{\circ}, \ 150^{\circ}\)です。
直線\(y = x\)となす鋭角が\(15^{\circ}\)である直線の傾きを求めてください。
答え
直線の傾きと\(\tan\theta\)の間には深い関係があります。 そもそも\(\tan\theta\)は単位円の定義で登場する赤線の傾きでしたね。 下の図を見てください。
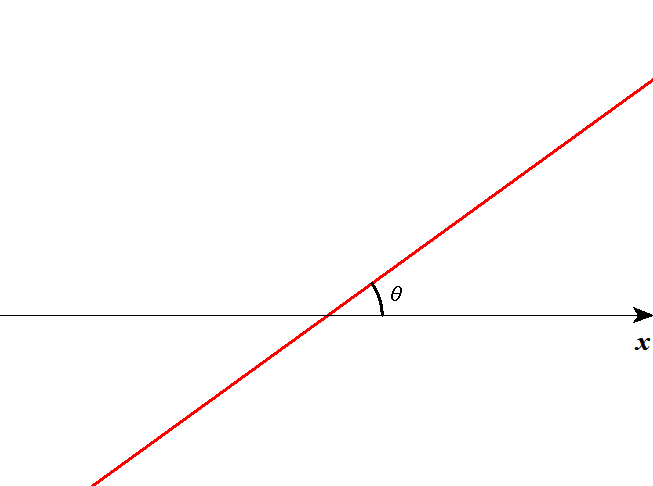
これは直線と\(x\)軸のなす角を\(\theta\)とした図です。 直線の傾きを\(m\)とすると,\(m\)は\(x\)の変化量に対する\(y\)の変化量ですね。 ところで,\(\tan\theta\)も\(x\)の変化量に対する\(y\)の変化量ですよね。 ということは,次が成り立ちます。
これは次図のように直線が右下がりの場合も同様です。 ただし,\(\theta\)のとり方に注意してください。 図のように右側からとる角のことを「\(x\)軸の正の向きとなす角」と表現します。
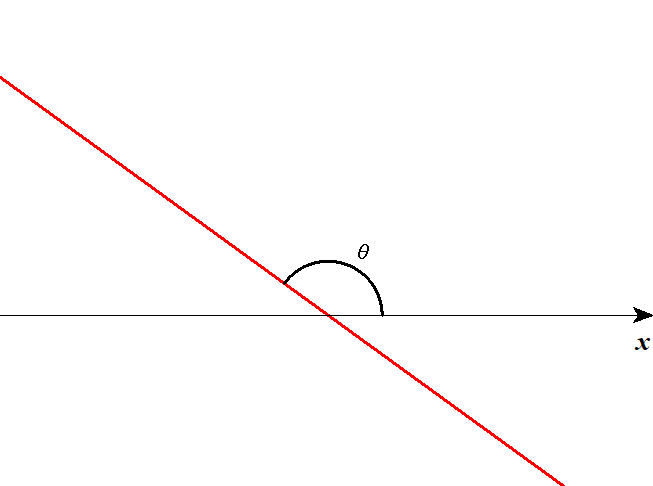
それでは,本題に入りましょう。 直線\(y = x\)が\(x\)軸の正の向きとなす角を\(\theta\)としましょう。 この直線となす鋭角が\(15^{\circ}\)である直線が,\(x\)軸の正の向きとなす角度は,\(\theta \pm 15^{\circ}\)の2つですね。
というわけで,\(\theta\)さえ求めれば答えが出ます。 直線\(y = x\)の傾きは\(1\)ですから,次の方程式が成り立ちます。
これを解くと\(\theta = 45^{\circ}\)です。 よって,直線\(y = x\)となす鋭角が\(15^{\circ}\)である直線が,\(x\)軸の正の向きとなす角度は\(30^{\circ}\),\(60^{\circ}\)です。 したがって,その傾きは\(\tan30^{\circ}\)と\(\tan60^{\circ}\),すなわち\(\displaystyle\frac{1}{\sqrt{3}}\),\(\sqrt{3}\)です。
