今回は,正弦定理・余弦定理を活用して,三角形の情報をうまく引き出す練習をします。
目次
三角形の要素確定
三角形には3つの辺と3つの角があります。 正弦定理や余弦定理を駆使して,これらの要素を特定することを考えてみましょう。
そもそも三角形の要素が確定するのはどんなときでしょう? 三角形というくらいですから,やっぱり3つの情報が必要です。 しかし,情報が3つあれば何でも良いわけではありません。
三角形のすべての要素は確定するのは,次の情報が揃うときです。
次のいずれかの情報が揃うとき,三角形の要素は確定する。
- 3辺の長さ
- 2辺の長さとその間の角度
- 1辺の長さと2つの角度
これ,見覚えありませんか? 三角形の合同条件もこんな感じの内容でしたね。 3つめについては,合同条件は「1辺とその両端の角」でしたが,2角が分かれば残りの1角も自動的に決まるので,同じことです。
これらの情報が揃っているとき,三角形は確定しますから,何らかの方法で他の要素も求められます。 角度は具体的に求められるとは限りませんが,少なくとも三角比の値は求められます。
それぞれの状況について具体的に考えていきます。 最後は確認問題で実践してくださいね。 定理という道具の使い方は,使って覚えるものです。
3辺から特定
まずは3辺の長さが分かっているとき,他の要素を求めることを考えましょう。 求めるべき情報は,3つの角度ですね。
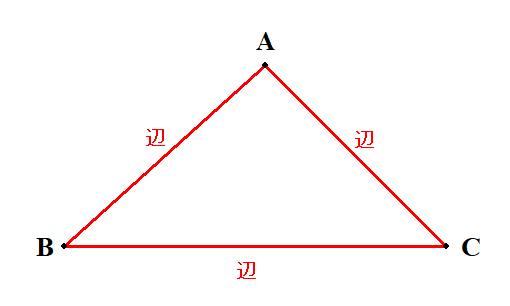
最初の角度は余弦定理で求めることになります。 余弦定理は次のような式でしたね。 これで少なくとも\(\cos\)の値は求められます。
この式を使えば,次のように\(\cos\)の値が求められます。
外接円の半径が分かっている場合を除いて,最初の角度は正弦定理では求められません。 正弦定理は次の式でしたね。
外接円の半径か,他の角度が少なくともひとつ分かっていれば,\(\sin\)の値が求められるわけです。 これらの情報がなければ,正弦定理は使えません。
角度をひとつ求めたら,残りの角度は正弦定理で求められます。 もちろん余弦定理を使ってもOKです。
最後の角度は,三角形の内角の和が\(180^{\circ}\)であることから求められます。 角度が具体的に求められないときは,正弦定理か余弦定理で三角比の値を求めるしかないですが。
ここでひとつ注意しておきたいことがあります。 \(\cos\)の値が分かれば,角度も決まります。 例えば\(\cos A = \displaystyle\frac{1}{2}\)なら\(A = 60^{\circ}\)ですね。
しかし\(\sin\)はそうはいきません。 \(\sin A = \displaystyle\frac{1}{2}\)が求められても\(A = 30^{\circ}\)か\(A = 150^{\circ}\)か分かりませんね。 \(\sin\)を求める場合は,角度の候補が鋭角と鈍角の2つあるかもしれませんから,あり得る角度かどうか検討する必要があるんです。
そこで役立つのが,次の三角形の性質です。
\(\triangle \mathrm{ABC}\)で,角の大小関係とその対辺の大小関係は一致する。 例えば,\(a < b\)と\(A < B\)は同値である。
この性質を使えば,\(\sin\)の値からありえる角度を検討できます。 正弦定理の計算は楽ですが,こういった検討が必要になりますから,初めから余弦定理を使うのもアリですね。
ちなみに,最大角以外では鈍角はありえません。 最大角の他にも鈍角があると,三角形の内角の和が\(180^{\circ}\)を超えてしまうからですね。 最大角について考えるときだけは,鈍角の可能性が出てくるわけです。
2辺とその間の角から特定
次に2辺とその間の角が分かっているとき,他の要素を求めることを考えましょう。 求めるべき情報は,残りの1辺と2角ですね。
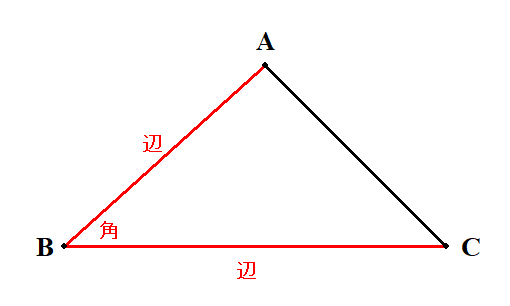
まずは残りの1辺の長さを求めます。 この辺の対角は分かっていますから,余弦定理が使えますね。
あとは残りの2角を正弦定理か余弦定理で求めるだけです。 最大辺の対角は鈍角の可能性がありますから,正弦定理を使う場合は注意してください。
1辺と2角から特定
最後に1辺と2角が分かっているとき,他の要素を求めることを考えましょう。 求めるべき情報は,残りの2辺と1角ですね。
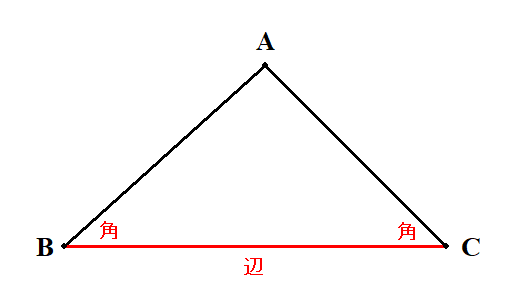
三角形の内角の和はいつも\(180^{\circ}\)ですから,2角が分かっているということは,すべての角度が分かっているということです。 角度の情報は好きなように使えますね。
あとは残りの2辺を求めるだけですが,ひとつめは正弦定理で求めるしかないですね。 余弦定理を使うには,他の2辺の情報が必要ですから。
最後の1辺は,正弦定理・余弦定理のどちらで求めてもOKです。 ただ計算が楽なのは正弦定理でしょうね。 角度を求めるときと違って,追加の検討も要りませんし。
鋭角・直角・鈍角三角形
三角形の要素が完全に確定できない場合でも,大体の形なら分かるかもしれません。 ここでは鋭角三角形・直角三角形・鈍角三角形の見分け方を学びます。
鋭角三角形とは,すべての角が鋭角である三角形です。 直角三角形は直角を含む三角形で,鈍角三角形は鈍角を含む三角形です。
これらを見分けるには,もちろん角度の情報が必要です。 しかしすべての角度を調べる必要はありません。 最大角だけを調べればOKです。
最大角が鋭角なら,他の角はそれより小さい鋭角ですから鋭角三角形です。 また最大角が直角・鈍角なら直角三角形・鈍角三角形なのは当然ですね。
まずどこが最大角なのか探す必要がありますね。 先ほど見た通り,三角形の角の大小関係とその対辺の大小関係は一致しますから,最大辺が分かれば最大角も分かります。
これで最大角の探し方も分かりました。 あとはその角が鋭角・直角・鈍角のどれなのか見分けるだけです。 その簡単な方法は余弦定理を使うことです。
\(\triangle\mathrm{ABC}\)の最大角を\(A\)としましょう。 余弦定理より,\(\cos A\)は次の式で求められます。
\(A\)は,\(\cos A\)が正のとき鋭角,\(0\)のとき直角,負のとき鈍角ですね。 つまり,\(\cos A\)の符号さえ分かれば良いのです。
\(\cos A\)を求める式を見ると,分母は常に正ですから,\(\cos A\)の符号は分子の符号だけで決まることが分かります。
したがって,ある三角形が鋭角三角形・直角三角形・鈍角三角形のどれかは,次のように見分けられます。
\(\triangle\mathrm{ABC}\)の最大角を\(A\)とする。 \(\triangle\mathrm{ABC}\)が鋭角三角形・直角三角形・鈍角三角形のどれかは,次の条件で決まる。
| 条件 | 三角形 |
|---|---|
| \(b^2 + c^2 - a^2 > 0\) | 鋭角三角形 |
| \(b^2 + c^2 - a^2 = 0\) | 直角三角形 |
| \(b^2 + c^2 - a^2 < 0\) | 鈍角三角形 |
これをわざわざ新しく覚える必要はありません。 次の点を押さえることが大切で,きちんと押さえていれば,上の判断方法も自然と分かります。
- 最大角から鋭角・直角・鈍角三角形を判別できる
- 最大角は最大辺の対角である
- 角が鋭角・直角・鈍角のどれかは\(\cos\)の符号で分かる
- \(\cos\)の値は余弦定理で求められる
確認問題
\(\triangle \mathrm{ABC}\)について,次の問いに答えてください。 外接円の半径を\(R\)とします。
-
\(a = 2\sqrt{3}\),\(b = 2\sqrt{2}\),\(c = \sqrt{6} - \sqrt{2}\)のとき,\(A\),\(B\),\(C\)を求めてください。
-
\(a = \sqrt{6}\),\(c = 2\sqrt{2}\),\(B = 30^{\circ}\)のとき,\(b\),\(A\),\(C\)を求めてください。
-
\(b = 4\),\(A = 75^{\circ}\),\(C = 60^{\circ}\)のとき,\(a\),\(c\),\(B\)を求めてください。
-
\(a = 2\sqrt{2}\),\(B = 30^{\circ}\),\(R = 2\)のとき,\(b\),\(c\),\(A\),\(C\)を求めてください。
答え
正弦定理・余弦定理を駆使して問題を解いていきましょう。
-
3辺の長さが与えられています。 適当に図をかいておきます。
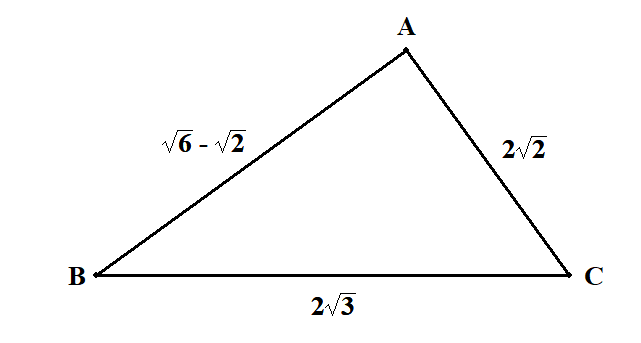
ここから角度を求めるのですが,正弦定理を使おうとすると情報が足りません。 余弦定理を使いましょう。 とりあえず\(\cos C\)を求めてみます。
\( \begin{align} \cos C &= \displaystyle\frac{(2\sqrt{2})^2 + (2\sqrt{3})^2 - (\sqrt{6} - \sqrt{2})^2}{2 \cdot 2\sqrt{2} \cdot 2\sqrt{3}} \\[5pt] &= \displaystyle\frac{8 + 12 - (6 - 2\sqrt{12} + 2)}{8\sqrt{6}} \\[5pt] &= \displaystyle\frac{12 + 4\sqrt{3}}{8\sqrt{6}} \\[5pt] &= \displaystyle\frac{3 + \sqrt{3}}{2\sqrt{6}} \\[5pt] &= \displaystyle\frac{3\sqrt{6} + 3\sqrt{2}}{12} \\[5pt] &= \displaystyle\frac{\sqrt{6} + \sqrt{2}}{4} \end{align} \)\(\cos C\)が見覚えのない値になってしまいました。 これでは\(C\)を求められません。 このように,\(\cos\)を計算しても角度が分からないこともあります。 ここは諦めて別の角の\(\cos\)を計算してみましょう。
\(\cos A\)を計算してみます。
\( \begin{align} \cos A &= \displaystyle\frac{(2\sqrt{2})^2 + (\sqrt{6} - \sqrt{2})^2 - (2\sqrt{3})^2}{2 \cdot 2\sqrt{2} \cdot (\sqrt{6} - \sqrt{2})} \\[5pt] &= \displaystyle\frac{8 + 6 - 2\sqrt{12} + 2 - 12}{8(\sqrt{3} - 1)} \\[5pt] &= \displaystyle\frac{4 - 4\sqrt{3}}{8(\sqrt{3} - 1)} \\[5pt] &= -\displaystyle\frac{4(\sqrt{3} - 1)}{8(\sqrt{3} - 1)} \\[5pt] &= -\displaystyle\frac{1}{2} \end{align} \)これなら\(A = 120^{\circ}\)だと分かりますね。
次は\(B\)を求めます。 余弦定理を使っても良いですが,ここは正弦定理を使ってみましょう。
\( \begin{align} \displaystyle\frac{a}{\sin A} &= \displaystyle\frac{b}{\sin B} \\[5pt] \sin B &= \displaystyle\frac{b}{a}\sin A \\[5pt] &= \displaystyle\frac{2\sqrt{2}}{2\sqrt{3}}\sin 120^{\circ} \\[5pt] &= \displaystyle\frac{\sqrt{2}}{\sqrt{3}}\cdot\displaystyle\frac{\sqrt{3}}{2} \\[5pt] &= \displaystyle\frac{1}{\sqrt{2}} \end{align} \)この式から\(B\)は\(45^{\circ}\)または\(135^{\circ}\)です。 しかし,\(A = 120^{\circ}\)であることから,\(B = 135^{\circ}\)はあり得ないことが分かります。 (三角形の内角の和は\(180^{\circ}\)ですね!) したがって,\(B = 45^{\circ}\)ですね。
残りの角は次の計算で求められます。
\( \begin{align} C &= 180^{\circ} - A - B \\[5pt] C &= 180^{\circ} - 120^{\circ} - 45^{\circ} \\[5pt] \textcolor{red}{C} &\textcolor{red}{=} \textcolor{red}{15^{\circ}} \end{align} \) -
2辺の長さとその間の角が与えられています。適当に図をかいておきます。
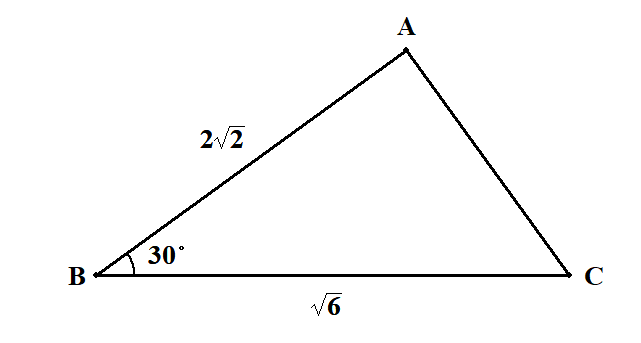
長さが分かっている辺の対角が分かっていないので,正弦定理は使えません。 余弦定理で残りの1辺の長さを求めます。
\( \begin{align} b^2 &= (2\sqrt{2})^2 + (\sqrt{6})^2 - 2 \cdot 2\sqrt{2} \cdot \sqrt{6} \cos 30^{\circ} \\[5pt] &= 8 + 6 - 8\sqrt{3} \cdot \displaystyle\frac{\sqrt{3}}{2} \\[5pt] &= 14 - 12 \\[5pt] &= 2 \\[5pt] \textcolor{red}{b} &\textcolor{red}{=} \textcolor{red}{\sqrt{2}} \end{align} \)
次は残りの2角を求めます。 正弦定理で\(A\)を求めてみましょう。
\( \begin{align} \displaystyle\frac{b}{\sin B} &= \displaystyle\frac{a}{\sin A} \\[5pt] \sin A &= \displaystyle\frac{a}{b}\sin B \\[5pt] &= \displaystyle\frac{\sqrt{6}}{\sqrt{2}}\sin 30^{\circ} \\[5pt] &= \sqrt{3}\cdot\displaystyle\frac{1}{2} \\[5pt] &= \displaystyle\frac{3}{2} \end{align} \)この式から\(A\)は\(60^{\circ}\)または\(120^{\circ}\)です。 しかし,最大辺が\(c\)であることから,最大角は\(C\)であるため,\(A\)が鈍角になることはあり得ません。 (\(A\)が鈍角なら\(C\)も鈍角になり,内角の和が\(180^{\circ}\)を超えます!) したがって,\(A = 60^{\circ}\)ですね。 \(c\)が最大辺であることは,\(c = 2\sqrt{2} = \sqrt{8}\)とすれば分かると思います。
残りの角は次の計算で求められます。
\( \begin{align} C &= 180^{\circ} - A - B \\[5pt] C &= 180^{\circ} - 60^{\circ} - 30^{\circ} \\[5pt] \textcolor{red}{C} &\textcolor{red}{=} \textcolor{red}{90^{\circ}} \end{align} \) -
1辺の長さと2角が与えられています。適当に図をかいておきます。
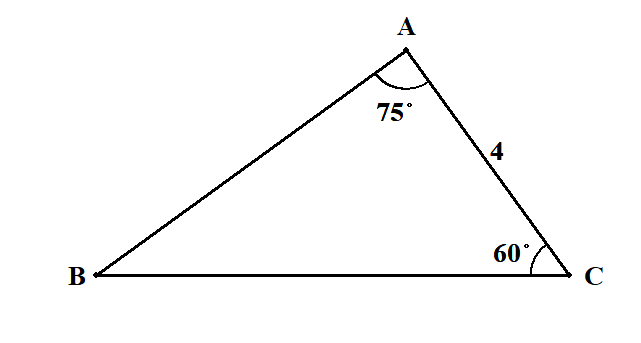
三角形の内角の和は絶対に\(180^{\circ}\)ですから,残りの1角が求められます。
\( \begin{align} B &= 180^{\circ} - A - C \\[5pt] B &= 180^{\circ} - 75^{\circ} - 60^{\circ} \\[5pt] \textcolor{red}{B} &\textcolor{red}{=} \textcolor{red}{45^{\circ}} \end{align} \)
残りの2辺を求めましょう。 その内のひとつめは,辺の情報が足りないので余弦定理では求められません。 正弦定理を使います。 ただし\(a\)は対角が\(75^{\circ}\)であり,三角比の値が分かりませんから,\(c\)の方を求めます。
\( \begin{align} \displaystyle\frac{c}{\sin C} &= \displaystyle\frac{b}{\sin B} \\[5pt] c &= \displaystyle\frac{b}{\sin B} \cdot \sin C \\[5pt] &= \displaystyle\frac{4}{\displaystyle\frac{1}{\sqrt{2}}} \cdot \displaystyle\frac{\sqrt{3}}{2} \\[5pt] &= 4\sqrt{2} \cdot \displaystyle\frac{\sqrt{3}}{2} \\[5pt] \textcolor{red}{c} &\textcolor{red}{=} \textcolor{red}{2\sqrt{6}} \end{align} \)
最後に\(a\)を求めます。 対角の三角比\(\cos 75^{\circ}\)が分からないので,\(\cos B\)か\(\cos C\)を利用するように余弦定理を使いましょう。
\( \begin{align} c^2 &= a^2 + b^2 - 2ab \cos C \\[5pt] (2\sqrt{6})^2 &= a^2 + 4^2 - 2 \cdot a \cdot 4 \cdot \displaystyle\frac{1}{2} \\[5pt] 24 &= a^2 + 16 - 4a \\[5pt] a^2 - 4a - 8 &= 0 \\[5pt] a &= -(-2) \pm \sqrt{(-2)^2 + 8} \\[5pt] &= 2 \pm \sqrt{12} \\[5pt] &= 2 \pm 2\sqrt{3} \end{align} \)\(a > 0\)ですから,\(a = 2 + 2\sqrt{3}\)です。
-
1辺の長さ,1角,外接円の半径が与えられています。適当に図をかいておきます。
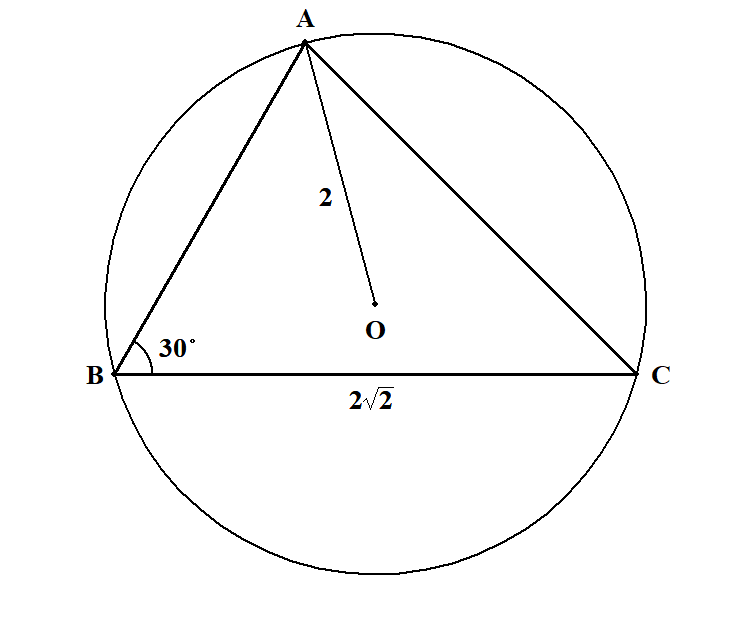
外接円の半径が分かっているので,正弦定理の出番です。 \(b\)を求めてみましょう。
\( \begin{align} \displaystyle\frac{b}{\sin B} &= 2R \\[5pt] b &= 2R \sin B \\[5pt] &= 2 \cdot 2 \cdot \displaystyle\frac{1}{2} \\[5pt] \textcolor{red}{b} &\textcolor{red}{=} \textcolor{red}{2} \end{align} \)
\(A\)も求められます。
\( \begin{align} \displaystyle\frac{a}{\sin A} &= 2R \\[5pt] \sin A &= \displaystyle\frac{a}{2R} \\[5pt] &= \displaystyle\frac{2\sqrt{2}}{2 \cdot 2} \\[5pt] &= \displaystyle\frac{1}{\sqrt{2}} \end{align} \)この式から\(A\)は\(45^{\circ}\)または\(135^{\circ}\)です。 まだどちらの可能性もあり得ますから,場合分けして考えましょう。
[1] \(A = 45^{\circ}\)の場合
このとき,\(A = 45^{\circ}\),\(C = 105^{\circ}\)ですね。 あとは\(c\)を求めるだけです。 \(C = 105^{\circ}\)の三角比の値が分かりませんから,正弦定理は使えません。 \(\cos C\)を使わずに済むように余弦定理を使いましょう。\( \begin{align} a^2 &= b^2 + c^2 - 2bc \cos A \\[5pt] (2\sqrt{2})^2 &= 2^2 + c^2 - 2 \cdot 2 \cdot c \cdot \displaystyle\frac{1}{\sqrt{2}} \\[5pt] 8 &= 4 + c^2 - 2\sqrt{2}c \\[5pt] c^2 - 2\sqrt{2}c - 4 &= 0 \\[5pt] c &= -(-\sqrt{2}) \pm \sqrt{(-\sqrt{2})^2 + 4} \\[5pt] c &= \sqrt{2} \pm \sqrt{6} \end{align} \)\(c > 0\)ですから,このとき\(c = \sqrt{6} + \sqrt{2}\)ですね。
[2] \(A = 135^{\circ}\)の場合
このとき,\(A = 135^{\circ}\),\(C = 15^{\circ}\)ですね。 あとは\(c\)を求めるだけです。 \(C = 15^{\circ}\)の三角比の値が分かりませんから,正弦定理は使えません。 \(\cos C\)を使わずに済むように余弦定理を使いましょう。\( \begin{align} a^2 &= b^2 + c^2 - 2bc \cos A \\[5pt] (2\sqrt{2})^2 &= 2^2 + c^2 - 2 \cdot 2 \cdot c \cdot \left(-\displaystyle\frac{1}{\sqrt{2}}\right) \\[5pt] 8 &= 4 + c^2 + 2\sqrt{2}c \\[5pt] c^2 + 2\sqrt{2}c - 4 &= 0 \\[5pt] c &= -\sqrt{2} \pm \sqrt{(\sqrt{2})^2 + 4} \\[5pt] c &= -\sqrt{2} \pm \sqrt{6} \end{align} \)\(c > 0\)ですから,このとき\(c = \sqrt{6} - \sqrt{2}\)ですね。
次の\(\triangle \mathrm{ABC}\)は鋭角三角形・直角三角形・鈍角三角形のどれか,それぞれ答えてください。
-
\(A = 32^{\circ}\),\(B = 53^{\circ}\)である三角形
-
\(a = 2\),\(b = 3\),\(c = 4\)である三角形
-
\(a = 3\),\(b = 4\),\(c = 5\)である三角形
-
\(a = 4\),\(b = 5\),\(c = 6\)である三角形
-
\(\sin A : \sin B : \sin C = 3 : 5 : 7\)である三角形
答え
最大角が鋭角・直角・鈍角のどれかを考えましょう。 具体的な角度が分からなくても,\(\cos\)の符号を見れば良いです。
-
残りの1角を求められますね。
\( \begin{align} C &= 180^{\circ} - A - B \\[5pt] &= 180^{\circ} - 32^{\circ} - 53^{\circ} \\[5pt] &= 95^{\circ} \end{align} \)よって,最大角である\(C\)が鈍角ですから,これは鈍角三角形です。
-
最大辺は\(c\)ですから,最大角は\(C\)です。 したがって,\(\cos C\)の符号を調べれば良いです。 \(\cos C\)は次の式で表せます。
\( \begin{align} \cos C = \displaystyle\frac{a^2 + b^2 - c^2}{2ab} \end{align} \)この分母は正ですから,分子の符号を調べれば良いですね。
\( \begin{align} a^2 + b^2 - c^2 &= 2^2 + 3^2 - 4^2 \\[5pt] &= 4 + 9 - 16 \\[5pt] &= -3 \end{align} \)したがって,\(\cos C < 0\)ですから,この三角形は鈍角三角形です。
-
最大辺は\(c\)ですから,最大角は\(C\)です。 したがって,\(\cos C\)の符号を調べれば良いです。 \(\cos C\)は次の式で表せます。
\( \begin{align} \cos C = \displaystyle\frac{a^2 + b^2 - c^2}{2ab} \end{align} \)この分母は正ですから,分子の符号を調べれば良いですね。
\( \begin{align} a^2 + b^2 - c^2 &= 3^2 + 4^2 - 5^2 \\[5pt] &= 9 + 16 - 25 \\[5pt] &= 0 \end{align} \)したがって,\(\cos C = 0\)ですから,この三角形は直角三角形です。
-
最大辺は\(c\)ですから,最大角は\(C\)です。 したがって,\(\cos C\)の符号を調べれば良いです。 \(\cos C\)は次の式で表せます。
\( \begin{align} \cos C = \displaystyle\frac{a^2 + b^2 - c^2}{2ab} \end{align} \)この分母は正ですから,分子の符号を調べれば良いですね。
\( \begin{align} a^2 + b^2 - c^2 &= 4^2 + 5^2 - 6^2 \\[5pt] &= 16 + 25 - 36 \\[5pt] &= 5 \end{align} \)したがって,\(\cos C > 0\)ですから,この三角形は鋭角三角形です。
-
最大角を知りたいですが,\(\sin\)の値の比しか分かりません。 正弦定理を使って,辺の情報に変換してみましょう。 正弦定理より,次の式が成り立ちます。
\( \begin{align} \displaystyle\frac{a}{\sin A} = \displaystyle\frac{b}{\sin B} = \displaystyle\frac{c}{\sin C} \end{align} \)したがって,次が成り立ちます。
\( \begin{align} a : b : c &= \sin A : \sin B : \sin C \\[5pt] &= 3 : 5 : 7 \end{align} \)よって,正の定数\(k\)を使って,\(a\),\(b\),\(c\)は次のように表せます。
\( \begin{align} a &= 3k \\[5pt] b &= 5k \\[5pt] c &= 7k \end{align} \)したがって,最大辺は\(c\)ですから,最大角は\(C\)です。 具体的な角度は分かっていませんから,余弦定理で\(\cos C\)の符号を調べましょう。
\( \begin{align} \cos C &= \displaystyle\frac{a^2 + b^2 - c^2}{2ab} \\[5pt] &= \displaystyle\frac{(3k)^2 + (5k)^2 - (7k)^2}{2 \cdot 3k \cdot 5k} \\[5pt] &= \displaystyle\frac{9k^2 + 25k^2 - 49k^2}{30k^2} \\[5pt] &= -\displaystyle\frac{15k^2}{30k^2} \\[5pt] &= -\displaystyle\frac{1}{2} \end{align} \)したがって,\(\cos C < 0\)ですから,この三角形は鈍角三角形です。
あなたの目線の先,距離は分かりませんが遠くに塔が見えます。 今いる場所と塔の距離が知りたいですが,実際に行こうと思うと遠そうで嫌になります。 工夫して距離を測ることにしました。
今いる場所から塔を見ると,真北から東に\(60^{\circ}\)の方角です。 真東に\(5(\sqrt{3} - 1)\)[\(\mathrm{km}\)]歩いてからもう一度塔を見ると,真北から東に\(45^{\circ}\)の方角でした。
これらの情報を基に,元いた場所から塔までの距離を求めてください。
答え
まずは問題の状況を図で表してみましょう。 塔の位置を\(\mathrm{A}\),元いた場所を\(\mathrm{B}\),歩いた後の場所を\(\mathrm{C}\)とすると,\(\triangle \mathrm{ABC}\)ができます。 三角形の問題に帰着できそうですね。 求めたいのは\(\mathrm{AB}\)の長さです。
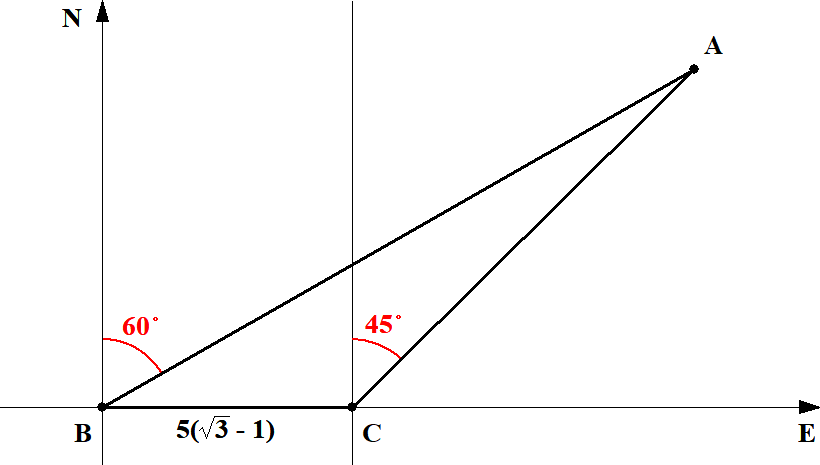
このままでは角度の情報が使いづらいので,下図のように三角形の内角として表します。
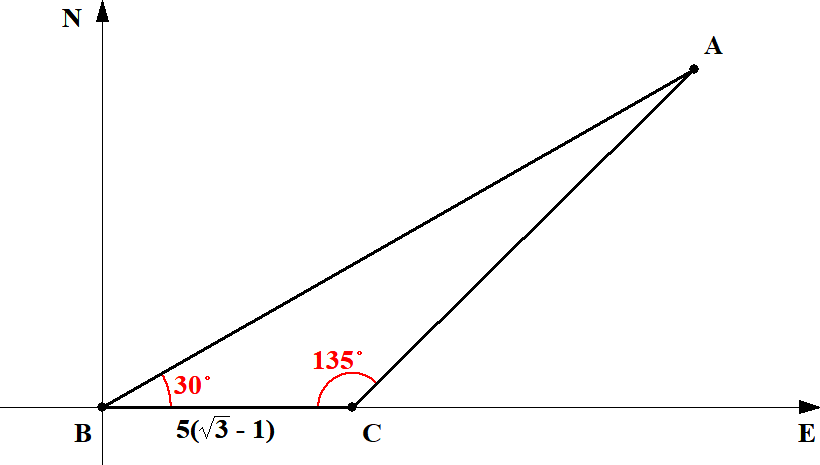
これで\(A = 15^{\circ}\)であることも分かりますね。 \(\mathrm{AB}\)を求めるためにはどうすれば良いでしょうか?
辺の長さが分かっているのは\(\mathrm{BC}\)のひとつだけです。 なので余弦定理は使えません。 また\(\mathrm{BC}\)の対角は\(15^{\circ}\)であり,三角比の値が分からないので正弦定理も使えません。
ここは初心に帰って,まず直角三角形をつくって三角比を使えるようにしましょう。 \(\mathrm{A}\)から\(\mathrm{BC}\)の延長線上に垂線\(\mathrm{AH}\)を下ろします。
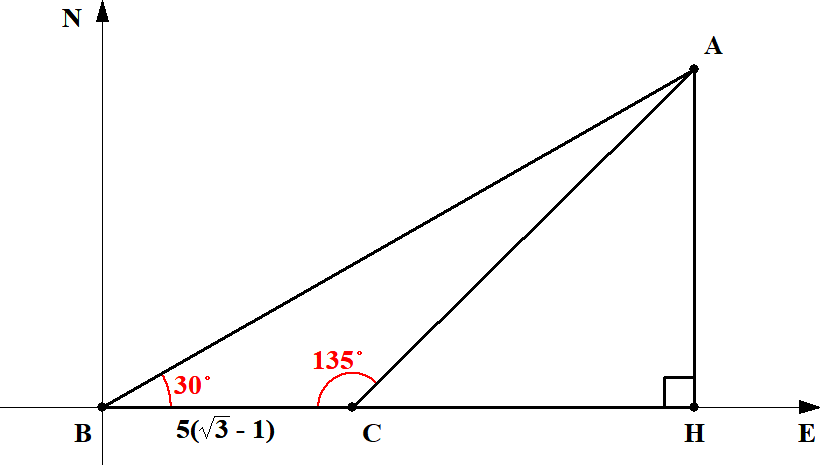
図から\(\angle\mathrm{ACH} = 45^{\circ}\)であり,\(\triangle\mathrm{ACH}\)が直角二等辺三角形であることが分かります。 \(\mathrm{AH} = \mathrm{CH} = x\)とおいてみます。
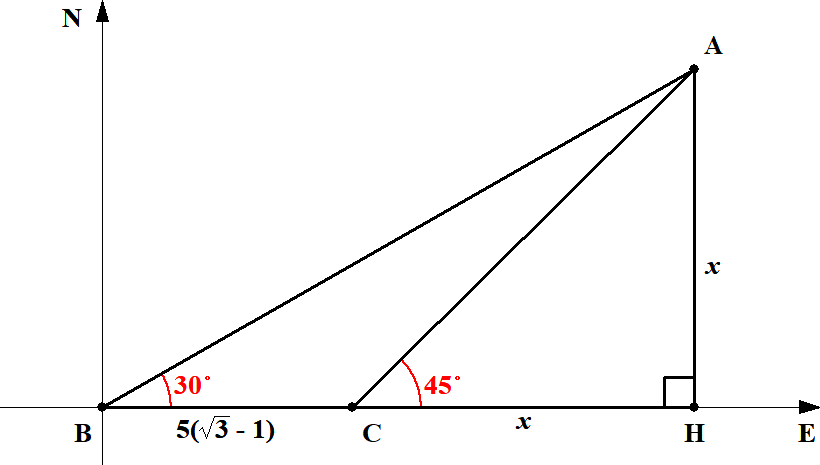
ここで直角三角形\(\triangle\mathrm{ABH}\)に注目すると,\(\tan 30^{\circ}\)を考えることで,今ある情報を繋げられそうです。
直角三角形\(\triangle\mathrm{ABH}\)の辺の情報がはっきりしてきました。 あとは\(\mathrm{AB}\)を求めるだけですね。
以上より,元いた場所から塔までの距離は\(10\)[\(\mathrm{km}\)]です。
この問題では正弦定理・余弦定理は使いませんでした。 しかし垂線をひいて,直角三角形をつくる発想はこれら定理と同じです。 公式の暗記だけでは,この問題に対応できないかもしれませんが,考え方さえ理解していれば応用がきくわけです。
