三角比の図形への応用として,三角形の辺や角度の結びつきを見てきました。 次は面積を考えてみましょう。 軽めの内容です。
目次
三角形の面積
三角形の面積を求める公式といえば,「底辺\(\times\)高さ\(\div 2\)」ですよね。 では,次の三角形の面積は分かりますか?
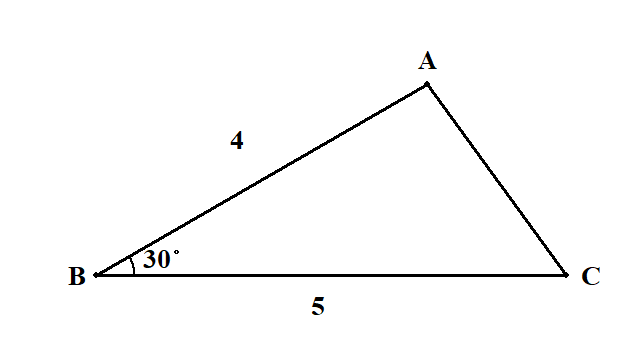
"高さ"の情報がありませんね。 ありませんが,なければつくれば良いのです。 頂点\(\mathrm{A}\)から辺\(\mathrm{BC}\)に垂線\(\mathrm{AH}\)を下ろしましょう。

\(\mathrm{AH}\)が高さですが,この長さは三角比を学んでいれば分かります。
したがって,この三角形の面積\(S\)は,次のように求められます。
このように,三角比を使えば高さが分かって,面積も分かります。 これを公式としてまとめてしまいましょう。
\(\triangle\mathrm{ABC}\)の面積\(S\)は,次の式で求められる。
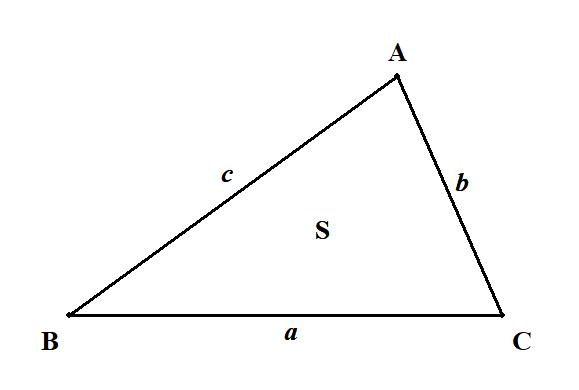
つまりある2辺とその間の角が分かれば,三角形の面積も分かるわけですね。 覚えやすい公式ですし,忘れてしまっても簡単につくれますね。
角が鈍角の場合も公式は成り立ちます。 確認問題にしておきますので,証明してみてください。
確認問題
\(C\)が鈍角である\(\triangle\mathrm{ABC}\)を考えます。 この三角形の面積\(S\)が次の式で表されることを証明してください。
答え
問題の三角形を図に表すと,次のような感じです。

この面積を求めるために,高さを求めます。 頂点\(\mathrm{A}\)から辺\(\mathrm{BC}\)の延長線上に垂線\(\mathrm{AH}\)を下ろせば,\(\mathrm{AH}\)が高さですね。
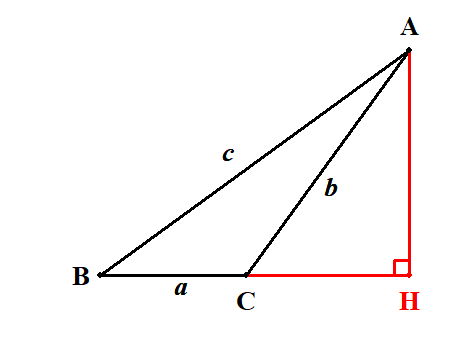
\(\angle\mathrm{ACH} = 180^{\circ} - C\)であることに注意すると,\(\mathrm{AH}\)は次のように求められます。
したがって,三角形の面積\(S\)は,次のように求められます。
次の\(\triangle\mathrm{ABC}\)の面積\(S\)を求めてください。
-
\(a = 4\),\(c = \sqrt{2}\),\(B = 135^{\circ}\)である三角形
-
\(a = 4\),\(b = 5\),\(c = 6\)である三角形
-
\(c = 3\),\(A = 45^{\circ}\),\(B = 15^{\circ}\)である三角形
答え
正確な図はかかなくて良いので,適当な図をかいて情報を整理しましょう。 2辺とその間の角が分かれば,三角形の面積を求められます。
-
問題の三角形を適当に図に表します。
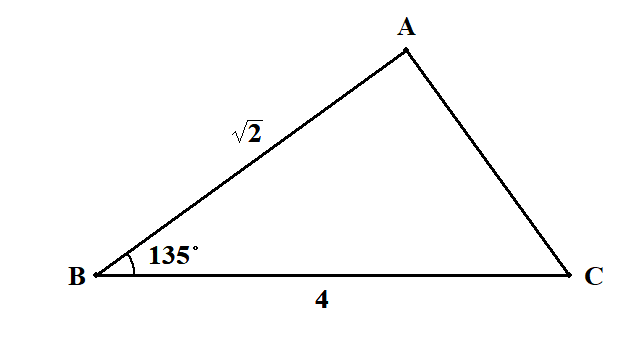
2辺とその間の角が分かっていますから,三角形の面積がすぐ求められます。
\( \begin{align} S &= \displaystyle\frac{1}{2}ca\sin B \\[5pt] &= \displaystyle\frac{1}{2} \cdot \sqrt{2} \cdot 4 \cdot \sin 135^{\circ} \\[5pt] &= 2\sqrt{2} \cdot \displaystyle\frac{1}{\sqrt{2}} \\[5pt] \textcolor{red}{S} &\textcolor{red}{=} \textcolor{red}{2} \end{align} \) -
問題の三角形を適当に図に表します。
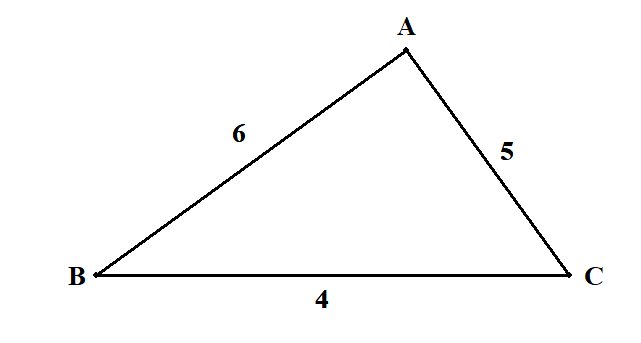
どこの角度も分かっていませんが,余弦定理を使えば\(\cos\)の値が分かります。 \(\cos A\)を求めてみましょう。
\( \begin{align} \cos A &= \displaystyle\frac{b^2 + c^2 - a^2}{2bc} \\[5pt] &= \displaystyle\frac{5^2 + 6^2 - 4^2}{2 \cdot 5 \cdot 6} \\[5pt] &= \displaystyle\frac{25 + 36 - 16}{60} \\[5pt] &= \displaystyle\frac{45}{60} \\[5pt] &= \displaystyle\frac{3}{4} \end{align} \)\(0^{\circ} < A < 180^{\circ}\)なので,\(\sin A > 0\)ですね。 このことに気を付けて\(\sin A\)を求めましょう。
\( \begin{align} \sin^2 A + \cos^2 A &= 1 \\[5pt] \sin^2 A &= 1 - \cos^2 A \\[5pt] &= 1 - \left(\displaystyle\frac{3}{4}\right)^2 \\[5pt] &= 1 - \displaystyle\frac{9}{16} \\[5pt] &= \displaystyle\frac{7}{16} \\[5pt] \sin A &= \displaystyle\frac{\sqrt{7}}{4} \end{align} \)これで三角形の面積を求める材料が揃いました。
\( \begin{align} S &= \displaystyle\frac{1}{2}bc\sin A \\[5pt] &= \displaystyle\frac{1}{2} \cdot 5 \cdot 6 \cdot \displaystyle\frac{\sqrt{7}}{4} \\[5pt] \textcolor{red}{S} &\textcolor{red}{=} \textcolor{red}{\displaystyle\frac{15\sqrt{7}}{4}} \end{align} \) -
問題の三角形を適当に図に表します。
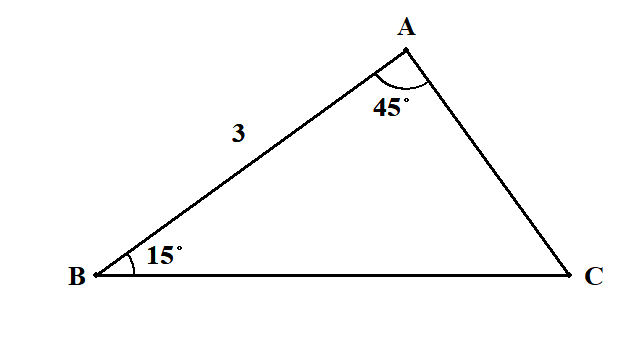
三角形の内角の和は\(180^{\circ}\)ですから,\(C = 120^{\circ}\)です。 三角形の面積を求めるには,辺の長さがもうひとつ必要ですね。 \(\sin A\)の値が分かりますから,\(b\)を求めて\(\displaystyle\frac{1}{2}bc\sin A\)を計算することを目標にしましょう。
しかし\(b\)を求めるにしても,対角の三角比の値が分からないので正弦定理は使えません。 かといって辺の長さがひとつしか分からないので余弦定理も使えません。 ここはまず\(a\)を正弦定理で求めて,その後\(b\)を余弦定理で求めることにします。
\( \begin{align} \displaystyle\frac{a}{\sin A} &= \displaystyle\frac{c}{\sin C} \\[5pt] a &= \displaystyle\frac{c}{\sin C} \cdot \sin A \\[5pt] &= \displaystyle\frac{3}{\displaystyle\frac{\sqrt{3}}{2}} \cdot \displaystyle\frac{1}{\sqrt{2}} \\[5pt] &= 3 \cdot \displaystyle\frac{2}{\sqrt{3}} \cdot \displaystyle\frac{1}{\sqrt{2}} \\[5pt] &= \sqrt{6} \end{align} \)
\(a\)が分かったので,次に余弦定理で\(b\)を求めます。 ただし\(\cos B\)の値は分からないので,\(\cos A\)を使うように計算します。
\( \begin{align} a^2 &= b^2 + c^2 - 2bc \cos A \\[5pt] (\sqrt{6})^2 &= b^2 + 3^2 - 2 \cdot b \cdot 3 \cos 45^{\circ} \\[5pt] 6 &= b^2 + 9 - 6b \cdot \displaystyle\frac{1}{\sqrt{2}} \\[5pt] 6 &= b^2 - 3\sqrt{2}b + 9 \\[5pt] b^2 - 3\sqrt{2}b + 3 &= 0 \\[5pt] b &= \displaystyle\frac{3\sqrt{2} \pm \sqrt{(-3\sqrt{2})^2 - 12}}{2} \\[5pt] &= \displaystyle\frac{3\sqrt{2} \pm \sqrt{6}}{2} \end{align} \)
\(B\)は最小角ですから,\(b\)は最小辺です。 \(3\sqrt{2} = \sqrt{18}\)であることに注意すると,\(4 < 3\sqrt{2} < 5\),\(2 < \sqrt{6} < 3\)ですから,次の不等式が成り立ちます。
\( \begin{align} 6 < 3\sqrt{2} + \sqrt{6} < 8 \\[5pt] 1 < 3\sqrt{2} - \sqrt{6} < 3 \end{align} \)したがって,次の不等式が成り立ちます。
\( \begin{align} 3 < \displaystyle\frac{3\sqrt{2} + \sqrt{6}}{2} < 4 \\[5pt] 0.5 < \displaystyle\frac{3\sqrt{2} - \sqrt{6}}{2} < 1.5 \end{align} \)この不等式より,\(b\)が最小辺であることから,\(b = \displaystyle\frac{3\sqrt{2} - \sqrt{6}}{2}\)です。
これで\(S\)を求める準備が整いました。
\( \begin{align} S &= \displaystyle\frac{1}{2} bc \sin A \\[5pt] &= \displaystyle\frac{1}{2} \cdot \displaystyle\frac{3\sqrt{2} - \sqrt{6}}{2} \cdot 3 \cdot \displaystyle\frac{1}{\sqrt{2}} \\[5pt] \textcolor{red}{S} &\textcolor{red}{=} \textcolor{red}{\displaystyle\frac{9 - 3\sqrt{3}}{4}} \end{align} \)
次の四角形\(\mathrm{ABCD}\)の面積\(S\)を求めてください。
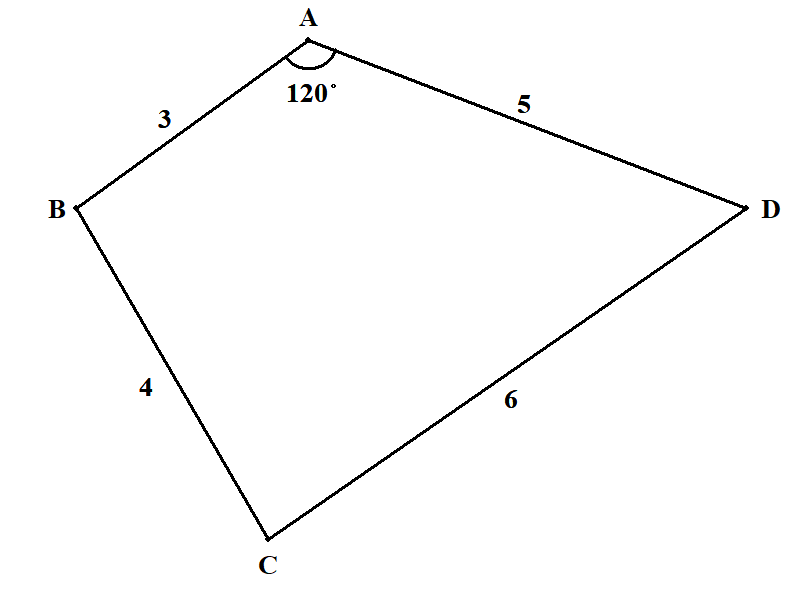
答え
こんな四角形の面積を求める公式は知りません。 でも持っている知識で解けるように工夫することはできます。 三角形なら扱えますから,次のように対角線\(\mathrm{BD}\)をひいて,2つの三角形に分割しましょう。

四角形に限らず,多角形はこのように三角形に分割できます。 三角形は基本的な図形であり,三角形が扱えれば多角形も扱えるわけです。
では四角形の面積\(S\)を考えていきましょう。 \(S\)は次のように表せますね。
この2つの三角形の面積が分かれば良いわけですね。 三角形の面積を求めるには,2辺とその間の角の情報が必要です。 \(\triangle\mathrm{ABD}\)の方は情報が揃っていますが,\(\triangle\mathrm{BCD}\)の方は情報が足りません。 まずは\(\sin C\)を求めることを目標にしましょう。
\(\triangle\mathrm{BCD}\)の内角はひとつも分かっていませんから,正弦定理は使えません。 なので余弦定理を使いたいですが,3辺すべての情報が必要になりますから,先に\(\mathrm{BD}\)を求めましょう。 これは\(\triangle\mathrm{ABD}\)に注目すると,余弦定理で求められますね。
\(\mathrm{BD} > 0\)ですから,\(\mathrm{BD} = 7\)ですね。 これで\(\cos C\)を求める準備ができました。 \(\triangle\mathrm{BCD}\)で余弦定理を使いましょう。
\(0^{\circ} < C < 180^{\circ}\)なので,\(\sin C > 0\)です。 このことに注意すると,\(\sin C\)は次のように求められます。
これで\(S\)を求める準備は整いました。 計算を進めましょう。
