空間図形の計量

はじめに

これまで三角比を利用して，主に三角形の計量を行ってきました。多角形についても，三角形に分割することで計量できました。これらは平面図形への応用でしたが，今回は空間図形への応用を考えます。

空間図形の復習

▼

これから空間図形の計量を考えます。まずは，空間図形にはあり，平面図形にはなかった「体積」について復習しておきましょう。

まずは柱体と錐体の体積を思い出しましょう。体積を求めるために必要な情報は，底面積と高さです。体積を求める式は，次の通りです。

柱体の体積

柱体の体積を\(V\)，底面積を\(S\)，高さを\(h\)とすると，次の式が成り立つ。

\( \begin{align} V = Sh \end{align} \)

補足柱体

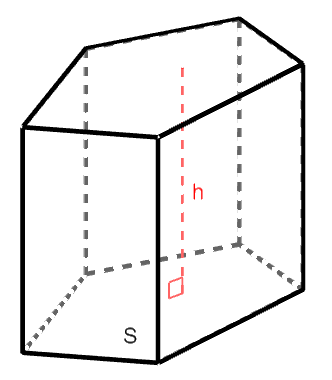
柱体とは，その名の通り柱状の空間図形です。底面と平行な平面で柱体を切ると，断面は底面と合同になります。底面が円なら円柱，多角形なら角柱というように，底面の図形によって呼び名が変わります。

柱体の体積の式は理解しやすいですね。底面と合同な図形が高さ分だけ積み重なっているわけですから，底面積に高さをかければ体積になるわけです。

錐体の体積

錐体の体積を\(V\)，底面積を\(S\)，高さを\(h\)とすると，次の式が成り立つ。

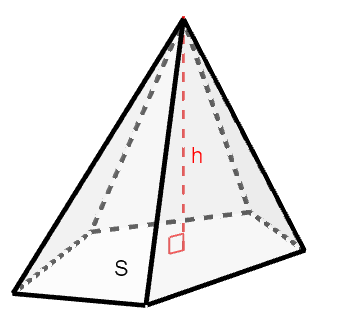
\( \begin{align} V = \displaystyle\frac{1}{3}Sh \end{align} \)

補足錐体

錐体とは，底面の各点と底面外の１点を結んだ線分を集めてできる空間図形で，とがった形になります。底面と平行な平面で錐体を切ると，断面は底面と相似になります。底面が円なら円錐，多角形なら角錐というように，底面の図形によって呼び名が変わります。

錐体の体積の式は，直感的にはなぜそうなるか分かりませんね。詳しい説明を理解するには，積分の知識が必要ですので，積分を学ぶまで待ってください。

面積の空間図形版である「表面積」についても確認しておきましょう。といっても確認するような公式はなく，表面の図形の面積を合計するだけですね。

言い方を変えれば，空間図形の表面積とは，その展開図の面積です。円錐の展開図には扇形が登場するので注意です。

柱体・錐体の他にも，体積や表面積の求め方を学んだ空間図形がありましたね。球です。球の体積・表面積も思い出しておきましょう。

球の体積・表面積

球の体積を\(V\)，表面積を\(S\)，半径を\(r\)とすると，次の式が成り立つ。

\( \begin{align} V = \displaystyle\frac{4}{3}\pi r^3 \end{align} \)

\( \begin{align} S = 4\pi r^2 \end{align} \)

補足球

球はある１点からの距離が等しい点の集まりです。その"ある１点"のことを中心といいます。どの角度から眺めても円に見える図形ですね。

身近な図形ですが，体積と表面積の式は直感的に理解できませんね。錐体の体積と同じく，この式の理解にも積分の知識が必要です。積分を学ぶまで待ってください。

空間図形の断面積

▲

▼

空間図形は３次元の図形であり，２次元の図形であった平面図形と比べると情報量が多いです。しかも３次元の図形を脳内でイメージするのは簡単ではありません。

そこで有効な手法が，空間図形を切って断面を考えることです。空間図形を考えるときは，まず断面図を考えるということが多いです。

というわけで，具体例として四面体の断面積を考えてみましょう。四面体とは，面が４つの空間図形のことで，三角錐ともいいます。三角比の応用でよく登場する図形です。

次の四面体\(\mathrm{OABC}\)を考えます。これは正四面体で，１辺の長さを\(6\)とします。

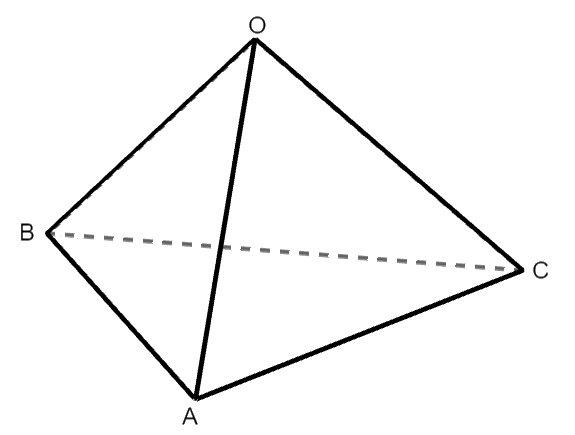
辺\(\mathrm{AB}\)から刃を入れて，この四面体の断面積を考えます。切り口は辺\(\mathrm{OC}\)を分割することになるので，その分割点を\(\mathrm{D}\)とします。 \(\mathrm{OD} = t\)として，断面\(\triangle\mathrm{ABD}\)の面積\(S\)を最小にする\(t\)を考えてみましょう。

つまり，断面をなるべく小さくする切り方を探す問題です。

与えられた図形は立体的ですが，あまり立体的に考える必要はありません。必要な平面を取り出して考えれば，今までと変わらず解くことができます。

問題となる断面は\(\triangle\mathrm{ABD}\)ですが，その面積を求めるには辺\(\mathrm{AD}\)，\(\mathrm{BD}\)の長さが必要です。 \(\triangle\mathrm{OAD} \equiv \triangle\mathrm{OBD}\)であることが図から分かりますから，\(\mathrm{AD} = \mathrm{BD}\)ですね。 \(\mathrm{AD}\)の方を求めてみましょう。

\(\mathrm{AD}\)を求めるには，\(\mathrm{AD}\)を含む平面である\(\triangle\mathrm{OAD}\)を考えれば良いです。 \(\triangle\mathrm{OAD}\)について，次の情報が分かっています。 \(\triangle\mathrm{OAC}\)が１辺の長さが\(6\)の正三角形であることに注意してください。

この三角形に対して余弦定理を使えば，\(\mathrm{AD}\)が求められますね。

\( \begin{align} \mathrm{AD}^2 &= \mathrm{OA}^2 + \mathrm{OD}^2 - 2 \mathrm{OA} \cdot \mathrm{OD} \cos 60^{\circ} \\[5pt] &= 6^2 + t^2 - 2 \cdot 6 \cdot t \cdot \displaystyle\frac{1}{2} \\[5pt] &= 36 + t^2 - 6t \\[5pt] \mathrm{AD} &= \sqrt{t^2 - 6t + 36} \end{align} \)

これで\(\mathrm{AD}\)，\(\mathrm{BD}\)の長さが分かりました。

\(\triangle\mathrm{ABD}\)の３辺の長さが分かったところで，情報を図にまとめてみましょう。

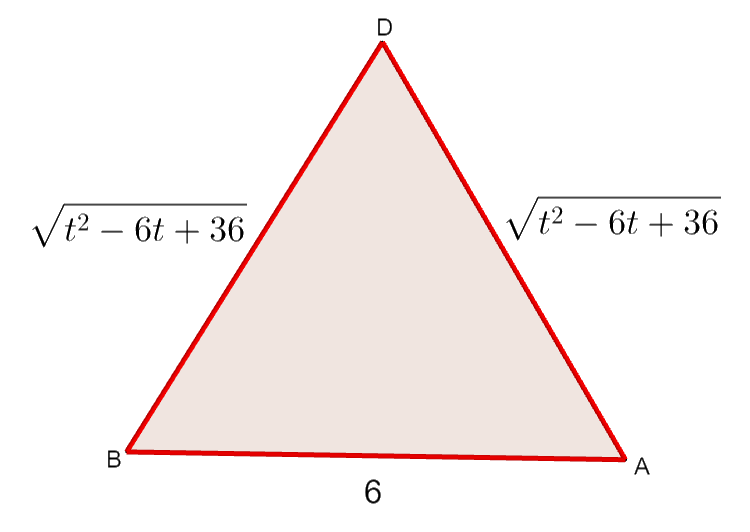
３辺の長さが分かれば，三角形の面積は求められます。本来なら余弦定理で好きな角の\(\cos\)を求めて，\(\sin\)に変換して，面積を求めるところですが，この三角形は二等辺三角形ですから，もっと簡単です。

図は省略しますが，頂点\(\mathrm{D}\)から対辺に垂線を下ろすと，ちょうど辺\(\mathrm{AB}\)の中点にぶつかります。したがって三角形の高さ\(h\)が次のように求められます。

\( \begin{align} h^2 &= (\sqrt{t^2 - 6t + 36})^2 - 3^2 \\[5pt] &= t^2 - 6t + 36 - 9 \\[5pt] &= t^2 - 6t + 27 \\[5pt] h &= \sqrt{t^2 - 6t + 27} \end{align} \)

これで断面積\(S\)が求められます。

\( \begin{align} S &= \displaystyle\frac{1}{2} \cdot 6 \cdot \sqrt{t^2 - 6t + 27} \\[5pt] &= 3\sqrt{t^2 - 6t + 27} \end{align} \)

このように空間図形に関する計量を行うときにも，新しい知識が必要になるわけではありません。平面図形を取り出して，今まで通り考えることができます。

あとは\(S\)を最小化する\(t\)を求めるだけです。ここからは三角比の空間図形への応用から離れますので，次項まで飛ばしてもＯＫです。

まず\(t\)の定義域を考えておきます。点\(\mathrm{D}\)が辺\(\mathrm{OC}\)上にあることを考えると，定義域が\(0 < t < 6\)であることが分かりますね。

\(S\)は根号を含む式ですが，それが最小になるのは，根号の中身が最小のときです。したがって，\(t^2 - 6t + 27\)が最小になる\(t\)を求めれば良いですね。この式を平方完成します。

\( \begin{align} t^2 - 6t + 27 = (t - 3)^2 + 18 \end{align} \)

このグラフは\(t = 3\)を軸とする下に凸の放物線であり，軸は定義域内にありますから，最小値をとる\(t\)が\(t = 3\)であるとわかりました。

空間図形の体積

▲

▼

次は空間図形の体積を考えましょう。体積を求める公式は復習しましたので，いかに底面積や高さを求めるかという問題になります。

先ほどと同じ四面体の体積を求めることにしましょう。次の四面体ですね。１辺の長さは\(6\)です。

この四面体の底面積を\(S\)，高さを\(h\)，体積を\(V\)として，順に求めていきましょう。

底面積は簡単ですね。底面は１辺が\(6\)の正三角形ですから，\(S\)は次のように求められます。

\( \begin{align} S &= \displaystyle\frac{1}{2} \cdot 6 \cdot 6 \cdot \sin 60^{\circ} \\[5pt] &= 18 \cdot \displaystyle\frac{\sqrt{3}}{2} \\[5pt] &= 9\sqrt{3} \end{align} \)

次は高さを考えます。頂点\(\mathrm{O}\)から底面に垂線\(\mathrm{OH}\)を下ろします。 \(\mathrm{OH}\)の長さが高さですね。

\(\mathrm{OH}\)の長さが知りたいわけですから，\(\mathrm{OH}\)を含む平面図形を探します。そのような図形として\(\triangle\mathrm{OHA}\)，\(\triangle\mathrm{OHB}\)，\(\triangle\mathrm{OHC}\)という直角三角形が考えられますね。

しかし，どれに注目しても\(\mathrm{HA}\)，\(\mathrm{HB}\)，\(\mathrm{HC}\)の長さが分からないせいで，\(\mathrm{OH}\)も求められません。１つの三角形を見ても分からないなら，３つの三角形の関係性に注目してみましょう。

この３つの三角形の斜辺は，もとは正四面体の辺ですから，全て等しいです。さらに辺\(\mathrm{OH}\)が共通ですから，これらの直角三角形は合同であり，次が成り立ちます。

\( \begin{align} \mathrm{AH} = \mathrm{BH} = \mathrm{CH} \end{align} \)

この等式から，点\(\mathrm{H}\)は底面の各頂点からの距離が等しい点であることが分かりました。それはどんな点かというと，底面の外接円の中心（外心）です。「距離が等しい」という情報から円を連想しましょう。

つまり\(\mathrm{AH}\)，\(\mathrm{BH}\)，\(\mathrm{CH}\)は底面の外接円の半径ですから，正弦定理でその長さを求められます。

\( \begin{align} &\quad \mathrm{AH} = \mathrm{BH} = \mathrm{CH} \\[5pt] &= \displaystyle\frac{6}{2\sin 60^{\circ}} \\[5pt] &= \displaystyle\frac{6}{2 \cdot \displaystyle\frac{\sqrt{3}}{2}} \\[5pt] &= \displaystyle\frac{6}{\sqrt{3}} \\[5pt] &= 2\sqrt{3} \end{align} \)

これで高さ\(h = \mathrm{OH}\)が求められますね。 \(\triangle\mathrm{OAH}\)で三平方の定理を使いましょう。

\( \begin{align} h^2 &= \mathrm{OA}^2 - \mathrm{AH}^2 \\[5pt] &= 6^2 - (2\sqrt{3})^2 \\[5pt] &= 36 - 12 \\[5pt] &= 24 \\[5pt] h &= 2\sqrt{6} \end{align} \)

底面積と高さが分かったので，正四面体の体積\(V\)が分かりますね。

\( \begin{align} V &= \displaystyle\frac{1}{3}Sh \\[5pt] &= \displaystyle\frac{1}{3} \cdot 9\sqrt{3} \cdot 2\sqrt{6} \\[5pt] &= 18\sqrt{2} \end{align} \)

なかなか大変な計算でしたね。空間図形を考えるときの流れを再度確認しておきましょう。

まず問題を解くために必要な要素を見極めます。体積を求めるなら底面積と高さが必要ですね。そして底面積を求めるには，底面の辺の長さや内角が必要というように，「これから何をすれば良いか」を明確にします。

必要な要素が分かったら，それを求めていきます。ただし立体的なままでは考えづらいので，その要素を含む平面図形を探して考えます。そうして注目する平面図形を切り替えながら，最終的な答えにたどり着くわけですね。

確認問題にも挑戦して練習しておきましょう。

確認問題

▲

１辺の長さが\(3\)である正四面体\(\mathrm{OABC}\)を考えます。この四面体の辺\(\mathrm{OB}\)上に点\(\mathrm{P}\)を，辺\(\mathrm{OC}\)上に点\(\mathrm{Q}\)をとります。このとき，\(\mathrm{OP} = 1\)，\(\mathrm{OQ} = 2\)を満たすようにします。

\(\triangle\mathrm{APQ}\)の面積\(S\)を求めてください。

答え

三角形の面積を求めるには，辺の長さや角度といった情報が必要です。図からは角度は分かりませんから，辺の長さを考えましょう。３辺の長さが分かれば，余弦定理で好きな角の\(\cos\)を求められます。

まず\(\mathrm{AP}\)を求めます。 \(\mathrm{AP}\)を含む平面図形を探すと，\(\triangle\mathrm{AOP}\)が見つかります。 \(\mathrm{OP} = 1\)，\(\mathrm{OA} = 3\)，\(\angle\mathrm{AOP} = 60^{\circ}\)が分かっていますから，余弦定理が使えますね。

\( \begin{align} \mathrm{AP}^2 &= 1^2 + 3^2 - 2 \cdot 1 \cdot 3 \cdot \cos 60^{\circ} \\[5pt] &= 1 + 9 - 6 \cdot \displaystyle\frac{1}{2} \\[5pt] &= 10 - 3 \\[5pt] &= 7 \\[5pt] \mathrm{AP} &= \sqrt{7} \end{align} \)

次に\(\mathrm{AQ}\)を求めます。 \(\mathrm{AQ}\)を含む平面図形を探すと，\(\triangle\mathrm{AOQ}\)が見つかります。 \(\mathrm{OQ} = 2\)，\(\mathrm{OA} = 3\)，\(\angle\mathrm{AOQ} = 60^{\circ}\)が分かっていますから，余弦定理が使えますね。

\( \begin{align} \mathrm{AQ}^2 &= 2^2 + 3^2 - 2 \cdot 2 \cdot 3 \cdot \cos 60^{\circ} \\[5pt] &= 4 + 9 - 12 \cdot \displaystyle\frac{1}{2} \\[5pt] &= 13 - 6 \\[5pt] &= 7 \\[5pt] \mathrm{AQ} &= \sqrt{7} \end{align} \)

次に\(\mathrm{PQ}\)を求めます。 \(\mathrm{PQ}\)を含む平面図形を探すと，\(\triangle\mathrm{POQ}\)が見つかります。 \(\mathrm{OP} = 1\)，\(\mathrm{OQ} = 2\)，\(\angle\mathrm{POQ} = 60^{\circ}\)が分かっていますから，余弦定理が使えますね。

\( \begin{align} \mathrm{PQ}^2 &= 1^2 + 2^2 - 2 \cdot 1 \cdot 2 \cdot \cos 60^{\circ} \\[5pt] &= 1 + 4 - 4 \cdot \displaystyle\frac{1}{2} \\[5pt] &= 5 - 2 \\[5pt] &= 3 \\[5pt] \mathrm{PQ} &= \sqrt{3} \end{align} \)

これで\(\triangle\mathrm{APQ}\)の３辺の長さが分かりました。面積を求めるには，どこかの角の\(\sin\)の値が必要です。 \(\angle\mathrm{PAQ} = \theta\)としましょう。３辺の長さの情報を利用するために，まずは余弦定理で\(\cos\theta\)の値を求めて，次に\(\sin\theta\)に変換しましょう。

\( \begin{align} \cos \theta &= \displaystyle\frac{\mathrm{AP}^2 + \mathrm{AQ}^2 - \mathrm{PQ}^2}{2 \mathrm{AP} \cdot \mathrm{AQ}} \\[5pt] &= \displaystyle\frac{(\sqrt{7})^2 + (\sqrt{7})^2 - (\sqrt{3})^2}{2 \cdot \sqrt{7} \cdot \sqrt{7}} \\[5pt] &= \displaystyle\frac{7 + 7 - 3}{14} \\[5pt] &= \displaystyle\frac{11}{14} \end{align} \)

\(0^{\circ} < \theta < 180^{\circ}\)なので\(\sin\theta > 0\)ですから，\(\sin\theta\)は次のように求められます。

\( \begin{align} \sin^2 \theta &= 1 - \cos^2 \theta \\[5pt] &= 1 - \left(\displaystyle\frac{11}{14}\right)^2 \\[5pt] &= 1- \displaystyle\frac{121}{196} \\[5pt] &= \displaystyle\frac{75}{196} \\[5pt] \sin\theta &= \displaystyle\frac{5\sqrt{3}}{14} \end{align} \)

これで面積を求めるために必要な情報が集まりました。

\( \begin{align} S &= \displaystyle\frac{1}{2} \cdot \mathrm{AP} \cdot \mathrm{AQ} \cdot \sin\theta \\[5pt] &= \displaystyle\frac{1}{2} \cdot \sqrt{7} \cdot \sqrt{7} \cdot \displaystyle\frac{5\sqrt{3}}{14} \\[5pt] \textcolor{red}{S} &\textcolor{red}{=} \textcolor{red}{\displaystyle\frac{5\sqrt{3}}{4}} \end{align} \)

ちなみに，三角形の合同に注目していれば，初めから\(\triangle\mathrm{APQ}\)が\(\mathrm{AP} = \mathrm{AQ}\)である二等辺三角形であることが分かり，途中の計算を楽に行うこともできました。

辺の長さを\(\mathrm{OA} = 4\)，\(\mathrm{OB} = 4\)，\(\mathrm{OC} = 4\)，\(\mathrm{AB} = 3\)，\(\mathrm{BC} = 2\sqrt{6}\)，\(\mathrm{CA} = 5\)とする四面体\(\mathrm{OABC}\)の体積\(V\)を求めてください。

答え

図をかくと次のようになります。正確じゃなくて良いので，とりあえず図にしておくと情報を整理しやすいです。

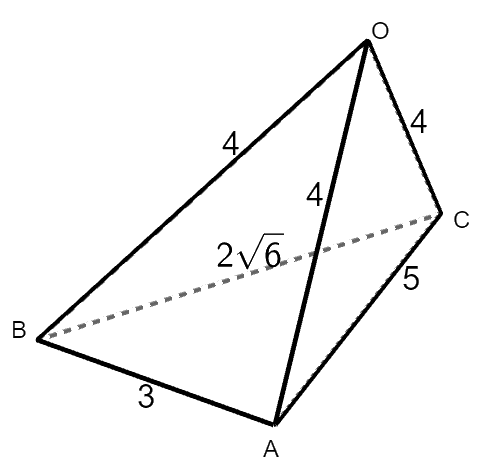
どこを底面とするかで難易度が変わりますが，上図のように，周りに同じ長さの辺が集まる頂点に注目して，その向かい側の面を底面とすると都合が良いです。その理由は，高さを考えやすくなることにあります。この先で確認していきましょう。

まず高さの前に底面積\(S\)を考えます。底面の３辺の長さが分かっていますから，あとはどこか好きな角の\(\sin\)の値が必要です。 \(\angle\mathrm{BAC} = \theta\)として，まずは余弦定理で\(\cos\theta\)を求めましょう。

\( \begin{align} \cos\theta &= \displaystyle\frac{\mathrm{AB}^2 + \mathrm{AC}^2 - \mathrm{BC}^2}{2\mathrm{AB} \cdot \mathrm{AC}} \\[5pt] &= \displaystyle\frac{3^2 + 5^2 - (2\sqrt{6})^2}{2 \cdot 3 \cdot 5} \\[5pt] &= \displaystyle\frac{9 + 25 - 24}{30} \\[5pt] &= \displaystyle\frac{1}{3} \end{align} \)

\(0^{\circ} < \theta < 180^{\circ}\)なので，\(\sin\theta > 0\)ですから，次のように\(\sin\theta\)が求められます。

\( \begin{align} \sin^2 \theta &= 1 - \cos^2 \theta \\[5pt] &= 1 - \left(\displaystyle\frac{1}{3}\right)^2 \\[5pt] &= 1 - \displaystyle\frac{1}{9} \\[5pt] &= \displaystyle\frac{8}{9} \\[5pt] \sin\theta &= \displaystyle\frac{2\sqrt{2}}{3} \end{align} \)

これで底面積\(S\)を求める準備が整いました。

\( \begin{align} S &= \displaystyle\frac{1}{2} \mathrm{AB} \cdot \mathrm{AC} \sin\theta \\[5pt] &= \displaystyle\frac{1}{2} \cdot 3 \cdot 5 \cdot \displaystyle\frac{2\sqrt{2}}{3} \\[5pt] &= 5\sqrt{2} \end{align} \)

次に高さ\(h\)を考えます。頂点\(\mathrm{O}\)から底面に垂線\(\mathrm{OH}\)を下ろします。この垂線の長さが高さになります。

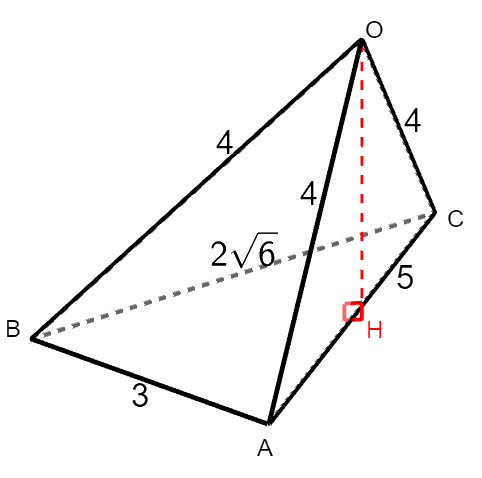
\(\mathrm{OH}\)の長さを知りたいので，\(\mathrm{OH}\)を含む平面図形を考えます。そんな図形として，直角三角形\(\triangle\mathrm{OHA}\)，\(\triangle\mathrm{OHB}\)，\(\triangle\mathrm{OHC}\)が考えられます。

これらの直角三角形は，斜辺がすべて同じ長さです。そうなるように底面を選んだわけです。また，辺\(\mathrm{OH}\)が共通ですから，これらの直角三角形はすべて合同です。したがって，次が成り立ちます。

\( \begin{align} \mathrm{AH} = \mathrm{BH} = \mathrm{CH} \end{align} \)

この等式は，底面\(\triangle\mathrm{ABC}\)の３つの頂点からの距離が等しい点が\(\mathrm{H}\)であることを表します。つまり点\(\mathrm{H}\)は底面の外接円の中心です。したがって，\(\mathrm{AH}\)，\(\mathrm{BH}\)，\(\mathrm{CH}\)は底面の外接円の半径ですから，正弦定理によりその長さが分かります。先ほど\(\sin\theta\)を求めたので利用します。

\( \begin{align} &\quad\mathrm{AH} = \mathrm{BH} = \mathrm{CH} \\[5pt] &= \displaystyle\frac{\mathrm{BC}}{2\sin\theta} \\[5pt] &= \displaystyle\frac{2\sqrt{6}}{2 \cdot \displaystyle\frac{2\sqrt{2}}{3}} \\[5pt] &= \sqrt{6} \cdot \displaystyle\frac{3}{2\sqrt{2}} \\[5pt] &= \displaystyle\frac{3\sqrt{3}}{2} \end{align} \)

これで高さ\(h\)を求める準備が整いました。直角三角形\(\triangle\mathrm{OHA}\)で三平方の定理を使います。

\( \begin{align} h^2 &= \mathrm{OA}^2 - \mathrm{AH}^2 \\[5pt] &= 4^2 - \left(\displaystyle\frac{3\sqrt{3}}{2}\right)^2 \\[5pt] &= 16 - \displaystyle\frac{27}{4} \\[5pt] &= \displaystyle\frac{37}{4} \\[5pt] h &= \displaystyle\frac{\sqrt{37}}{2} \end{align} \)

これで体積\(V\)を求める準備が整いました。

\( \begin{align} V &= \displaystyle\frac{1}{3}Sh \\[5pt] &= \displaystyle\frac{1}{3} \cdot 5\sqrt{2} \cdot \displaystyle\frac{\sqrt{37}}{2} \\[5pt] \textcolor{red}{V} &\textcolor{red}{=} \textcolor{red}{\displaystyle\frac{5\sqrt{74}}{6}} \end{align} \)

半径\(R\)の球に内接する正四面体の体積\(V\)を求めてください。

答え

題意の正四面体を\(\mathrm{OABC}\)とし，その１辺の長さを\(a\)とします。 \(a\)と\(R\)の結びつきを探して，四面体の体積\(V\)を求めましょう。

とりあえず四面体の体積\(V\)を\(a\)で表してしまいましょう。頂点\(\mathrm{O}\)から底面\(\triangle\mathrm{ABC}\)に向けて垂線\(\mathrm{OH}\)を下ろします。

直角三角形\(\triangle\mathrm{OHA}\)，\(\triangle\mathrm{OHB}\)，\(\triangle\mathrm{OHC}\)は斜辺の長さが同じで，辺\(\mathrm{OH}\)が共通なので合同です。したがって\(\mathrm{AH} = \mathrm{BH} = \mathrm{CH}\)であり，点\(\mathrm{H}\)は底面\(\triangle\mathrm{ABC}\)の外接円の中心ですから，\(\mathrm{AH}\)，\(\mathrm{BH}\)，\(\mathrm{CH}\)はその外接円の半径であり，正弦定理で長さが分かります。

\( \begin{align} &\quad \mathrm{AH} = \mathrm{BH} = \mathrm{CH} \\[5pt] &= \displaystyle\frac{a}{2\sin 60^{\circ}} \\[5pt] &= \displaystyle\frac{a}{2 \cdot \displaystyle\frac{\sqrt{3}}{2}} \\[5pt] &= \displaystyle\frac{a}{\sqrt{3}} \end{align} \)

\(\triangle\mathrm{OHA}\)で三平方の定理を使うと，四面体の高さ\(\mathrm{OH}\)が分かります。

\( \begin{align} \mathrm{OH}^2 &= \mathrm{OA}^2 - \mathrm{AH}^2 \\[5pt] &= a^2 - \left(\displaystyle\frac{a}{\sqrt{3}}\right) \\[5pt] &= a^2 - \displaystyle\frac{a^2}{3} \\[5pt] &= \displaystyle\frac{2}{3}a^2 \\[5pt] \mathrm{OH} &= \displaystyle\frac{\sqrt{6}}{3}a \end{align} \)

また底面である\(\triangle\mathrm{ABC}\)の面積は次のように求められます。

\( \begin{align} \triangle\mathrm{ABC} &= \displaystyle\frac{1}{2} \cdot \mathrm{AB} \cdot \mathrm{AC} \sin 60^{\circ} \\[5pt] &= \displaystyle\frac{1}{2} \cdot a \cdot a \cdot \displaystyle\frac{\sqrt{3}}{2} \\[5pt] &= \displaystyle\frac{\sqrt{3}}{4}a^2 \end{align} \)

したがって，四面体の体積\(V\)は次のようになります。

\( \begin{align} V &= \displaystyle\frac{1}{3} \cdot \triangle\mathrm{ABC} \cdot \mathrm{OH} \\[5pt] &= \displaystyle\frac{1}{3} \cdot \displaystyle\frac{\sqrt{3}}{4}a^2 \cdot \displaystyle\frac{\sqrt{6}}{3}a \\[5pt] &= \displaystyle\frac{\sqrt{2}}{12}a^3 \end{align} \)

次に\(a\)と\(R\)の関係を考えて，\(V\)を\(R\)で表せるようにします。この四面体は半径\(R\)の球に内接しています。この球の中心を\(\mathrm{P}\)とするとき，\(\mathrm{P}\)と四面体の位置関係を考えれば，\(a\)と\(R\)の関係にたどり着くはずです。

四面体は球に内接していますから，その４頂点はすべて球上にあります。したがって，\(\mathrm{P}\)はこの４頂点との距離が等しい点です。しかし，そんな点の在処を探すのは難しそうです。まずは３頂点との距離が等しい点だけ考えてみましょう。

３頂点との距離が等しい点なら既にひとつ知っています。点\(\mathrm{H}\)です。この点は\(\triangle\mathrm{ABC}\)の外接円の中心でしたから，その３頂点との距離が等しいわけですね。しかし，\(\mathrm{OH} \neq \mathrm{AH}\)ですから，この点が球の中心\(\mathrm{P}\)と一致するわけではありません。ですが，\(\mathrm{P}\)を探す手掛かりにはなります。

点\(\mathrm{H}\)から\(\triangle\mathrm{ABC}\)に垂直な直線をひくと，この直線上の点\(\mathrm{X}\)は，３点\(\mathrm{A}\)，\(\mathrm{B}\)，\(\mathrm{C}\)との距離が等しいままです。 \(\triangle\mathrm{XHA}\)，\(\triangle\mathrm{XHB}\)，\(\triangle\mathrm{XHC}\)が合同であることから分かります。

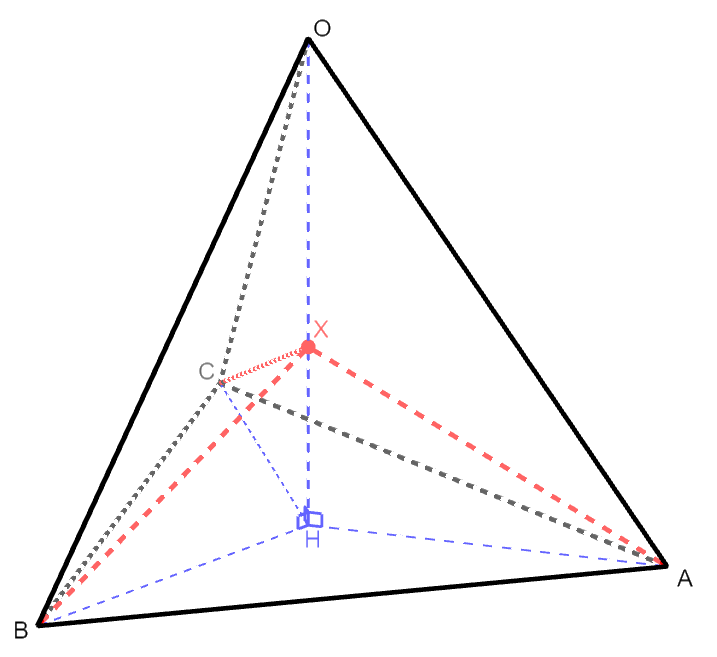
点\(\mathrm{X}\)を移動させて，四面体の４頂点との距離が等しくなるポイントが\(\mathrm{P}\)ですね。 \(\mathrm{OH} > \mathrm{AH}\)であることを考慮すると，\(\mathrm{P}\)は\(\mathrm{H}\)よりも\(\mathrm{O}\)に近い位置にありますから，\(\mathrm{P}\)は線分\(\mathrm{OH}\)上にあります。

したがって，直角三角形\(\triangle\mathrm{PAH}\)の３辺の長さは次のように表せます。

\( \begin{eqnarray} \left\{ \begin{array}{l} \mathrm{AP} = R\\ \mathrm{PH} = \mathrm{OH} - \mathrm{OP} = \displaystyle\frac{\sqrt{6}}{3}a - R\\ \mathrm{AH} = \displaystyle\frac{a}{\sqrt{3}} \end{array} \right. \end{eqnarray} \)

この直角三角形に三平方の定理を適用することで，\(a\)と\(R\)の関係が分かります。 \(a \neq 0\)であることに注意してください。

\( \begin{align} \mathrm{PH}^2 + \mathrm{AH}^2 &= \mathrm{AP}^2 \\[5pt] \left(\displaystyle\frac{\sqrt{6}}{3}a - R\right)^2 + \left(\displaystyle\frac{a}{\sqrt{3}}\right)^2 &= R^2 \\[5pt] \displaystyle\frac{2}{3}a^2 - \displaystyle\frac{2\sqrt{6}}{3}aR + R^2 + \displaystyle\frac{a^2}{3} &= R^2 \\[5pt] \displaystyle\frac{2}{3}a^2 - \displaystyle\frac{2\sqrt{6}}{3}aR + \displaystyle\frac{a^2}{3} &= 0 \\[5pt] a^2 - \displaystyle\frac{2\sqrt{6}}{3}aR &= 0 \\[5pt] a(a - \displaystyle\frac{2\sqrt{6}}{3}R) &= 0 \\[5pt] a - \displaystyle\frac{2\sqrt{6}}{3}R &= 0 \\[5pt] a &= \displaystyle\frac{2\sqrt{6}}{3}R \end{align} \)

これで\(V\)を\(R\)で表せるようになりました。

\( \begin{align} V &= \displaystyle\frac{\sqrt{2}}{12}a^3 \\[5pt] &= \displaystyle\frac{\sqrt{2}}{12} \cdot \left(\displaystyle\frac{2\sqrt{6}}{3}R\right)^3 \\[5pt] &= \displaystyle\frac{\sqrt{2}}{12} \cdot \displaystyle\frac{48\sqrt{6}}{27}R^3 \\[5pt] \textcolor{red}{V} &\textcolor{red}{=} \textcolor{red}{\displaystyle\frac{8\sqrt{3}}{27}R^3} \end{align} \)