データの分析について少しだけ扱います。 数学Ⅰではごく簡単なことしか扱いませんが,基本は大事です。 まずはデータの簡単な整理方法を学びましょう。
目次
データ
世の中には様々なデータがあります。 例えば,テストの点数や毎日の天気などをまとめたものです。
データの中身は,点数であれば\(80\)点や\(50\)点,天気であれば晴れや雨など,様々な形をとります。 前者のように定量的な値で与えられるものを量的データ,後者のように数値で測定できず,分類や種類を区別するものを質的データといいます。
質的データも数値で表すことはできます。 例えば天気について晴れを\(0\),雨を\(1\)というように表すことにすれば良いのです。
しかし,この数値は晴れや雨といった名前の代わりでしかなく,大小関係の比較や合計の計算などに意味はありません。 なので便宜的に数値で表したとしても,量的データとはいえません。
今後扱うデータは,主に量的データです。
自然とデータという言葉を使ってきましたが,データは様々な調査の結果得られるものとの認識しかないかもしれませんね。 改めて用語の意味を確認しておきましょう。
調査対象の性質を表す数量を変量といいます。 データとは,変量の具体的な値の集まりです。
例えば,テストの点数や気温というのは変量です。 そして,あるクラスの生徒が受けたテストの点数を集めたものや,ある月の毎日の気温を集めたものはデータです。 用語の違いに注意しましょう。
度数分布表
データがバラバラと存在するだけでは,その意味するところは分かりません。 ここではデータを整理する方法を学びましょう。
簡単な整理方法としては,データの値の大きさで分けるやり方があります。 データの値の範囲をいくつかに区切って,それぞれの区間に属するデータの個数を調べることで,データの分布を明らかにするのです。
この方法ではデータをいくつかの区間に区切るのですが,この区間を階級といい,区間の幅を階級幅,階級の数を階級数といいます。 階級の真ん中の値をその階級の代表とし,その値を階級値といいます。
各階級に属するデータの個数を度数といい,各階級の度数がいくつなのかまとめた表を度数分布表といいます。 階級数や階級幅をどう取るかで度数分布表の形は変わります。
具体例を見てみましょう。 次のデータは,あるクラスの\(20\)人の生徒のテストの点数を表しているとします。
このデータを度数分布表に整理したいと思います。 階級を\(0\)から区切り,階級幅を\(20\)とした場合,度数分布表は次のようになります。
| 階級(点) | 度数 | ||||
|---|---|---|---|---|---|
| \(0\) | 以上 | ~ | \(20\) | 未満 | \(1\) |
| \(20\) | ~ | \(40\) | \(3\) | ||
| \(40\) | ~ | \(60\) | \(6\) | ||
| \(60\) | ~ | \(80\) | \(6\) | ||
| \(80\) | ~ | \(100\) | \(4\) | ||
| 計 | \(20\) | ||||
元はバラついたデータでしたが,度数分布表に整理したことで,全体的な点数の傾向が見えてきましたね。 次項でそれを視覚化するヒストグラムを学びます。
ちなみに,階級値は上から順に\(10\),\(30\),\(50\),\(70\),\(90\)ですね。
ヒストグラム
度数分布表をかくことで,バラついて見えたデータを整理することができました。 しかし,特にデータが大きい場合などは,表に整理してもデータの分布の形は見えてきません。
表のままでは見づらいのなら,その情報をグラフ化すると良いでしょう。 分布の形が視覚的に表されるはずです。
一般に度数分布表からは,ヒストグラムまたは柱状グラフと呼ばれるグラフを描きます。 先ほどのテストの点数のデータをヒストグラムにすると,次のようになります。
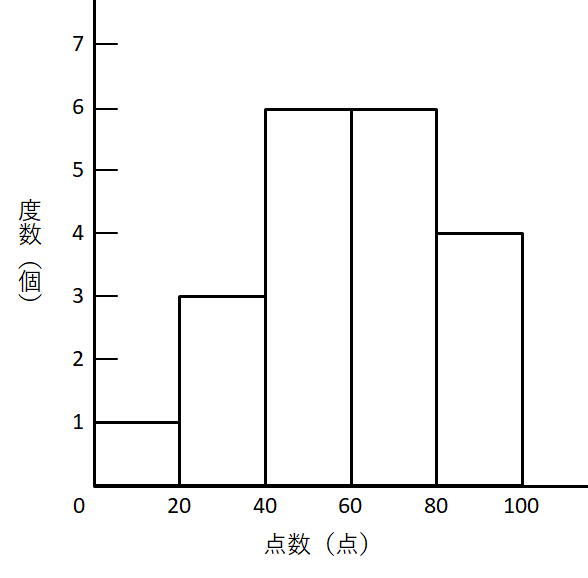
ヒストグラムの描き方は見ての通りです。 各階級に対して,その度数を高さとする長方形を描きます。 長方形の大きさからデータの分布の仕方が見えてきますね。
階級幅が一定の場合は,ヒストグラムの長方形の高さは,その階級に対応する度数になります。 目にするのはたいてい階級幅が一定の場合でしょうから,この認識だけでも十分です。
ですが階級幅が一定でない場合には,長方形の高さではなく,面積を度数と比例するようにします。 普通は階級幅を一定にするので気にしなくても良いですが,もしそうでないヒストグラムを見かけたら,見方に注意してください。
他の度数分布表
度数の具体的な大きさよりも,それが全体に占める割合の方が有益な情報になる場面は多いです。 各階級の度数が全体に占める割合を相対度数といい,階級ごとの相対度数をまとめた表を相対度数分布表といいます。
先ほど使ったテストの点数のデータを例にすると,相対度数分布表は次のようになります。
| 階級(点) | 相対度数 | ||||
|---|---|---|---|---|---|
| \(0\) | 以上 | ~ | \(20\) | 未満 | \(0.05\) |
| \(20\) | ~ | \(40\) | \(0.15\) | ||
| \(40\) | ~ | \(60\) | \(0.3\) | ||
| \(60\) | ~ | \(80\) | \(0.3\) | ||
| \(80\) | ~ | \(100\) | \(0.2\) | ||
| 計 | \(1\) | ||||
各階級の相対度数が,度数をデータの大きさである\(20\)で割った値になっていることを確認してください。 (データに含まれる値の個数をデータの大きさといいます。)
度数と相対度数の他に,よく使われるのが累積度数と累積相対度数です。 それを表にしたものを累積度数分布表,累積相対度数分布表といいます。
累積度数とは,度数を下の階級から順に積み上げたときの度数の合計です。 つまり,その階級以下の度数の合計ですね。 使い道はあとで説明しますから,まずは具体例を見てください。 先ほどのテストの点数のデータを使います。
| 階級(点) | 累積度数 | |
|---|---|---|
| \(20\) | 未満 | \(1\) |
| \(40\) | \(4\) | |
| \(60\) | \(10\) | |
| \(80\) | \(16\) | |
| \(100\) | \(20\) | |
累積度数分布表を見ると,ある範囲の点数をとった人数ではなく,ある点数以下(未満)をとった人数が分かります。 これまでの表と違って,階級の値の範囲は上限だけ書けば良く,最後に合計を記入する行は不要です。
累積度数分布表が役立つのは,ある値に達しているかどうかを調べたい場合です。 例えば年収なんかは,\(300\)万円以上\(400\)万円未満の人数よりも,\(400\)万円未満の人数を調べたい場面も多いです。
累積相対度数は累積度数が全体に占める割合ですが,改めて説明は必要ないでしょう。 先ほどの年収の例では,実際には\(400\)万円未満の具体的な人数よりも,その人たちが全体の何%なのかが気になる場合,累積相対度数分布表を使います。
確認問題
次のデータはある\(20\)人の身長(単位は\(\mathrm{cm}\))を表しています。 このデータの度数分布表を作成し,ヒストグラムを描いてください。 ただし,階級は\(140\)\(\mathrm{cm}\)から区切りはじめ,階級幅は\(10\)\(\mathrm{cm}\)とします。
答え
めんどくさいですが,各階級に入る値の個数を数えましょう。 度数分布表は次のようになります。
| 階級(\(\mathrm{cm}\)) | 度数 | ||||
|---|---|---|---|---|---|
| \(140\) | 以上 | ~ | \(150\) | 未満 | \(2\) |
| \(150\) | ~ | \(160\) | \(6\) | ||
| \(160\) | ~ | \(170\) | \(7\) | ||
| \(170\) | ~ | \(180\) | \(4\) | ||
| \(180\) | ~ | \(190\) | \(1\) | ||
| 計 | \(20\) | ||||
これをヒストグラムにすると,次のようになります。
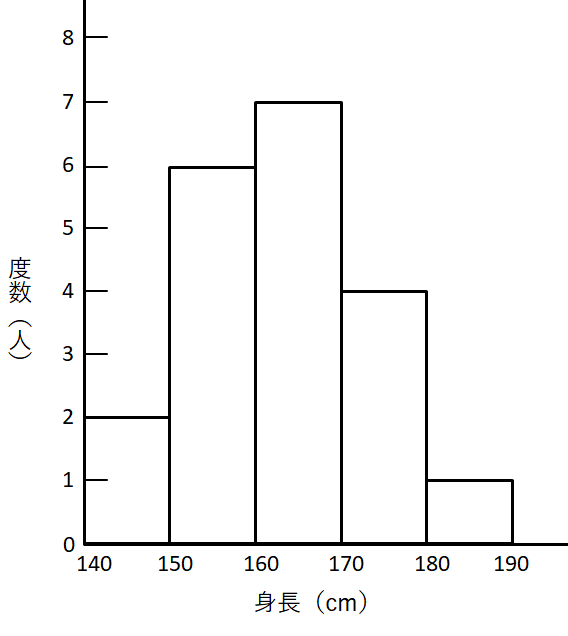
ちなみに,現実にはデータはもっと膨大ですから,人力で数えるのは厳しいです。 普通はプログラムで処理します。
あるグループに属す生徒たちに5教科の試験を受けてもらい,各生徒の総得点のデータを次のように度数分布表に整理しました。 この度数分布表について,(1)~(3)に答えてください。
| 階級(点) | 度数 | ||||
|---|---|---|---|---|---|
| \(0\) | 以上 | ~ | \(50\) | 未満 | \(3\) |
| \(50\) | ~ | \(100\) | \(8\) | ||
| \(100\) | ~ | \(150\) | \(15\) | ||
| \(150\) | ~ | \(200\) | \(36\) | ||
| \(200\) | ~ | \(250\) | \(61\) | ||
| \(250\) | ~ | \(300\) | \(101\) | ||
| \(300\) | ~ | \(350\) | \(162\) | ||
| \(350\) | ~ | \(400\) | \(81\) | ||
| \(400\) | ~ | \(450\) | \(26\) | ||
| \(450\) | ~ | \(500\) | \(7\) | ||
| 計 | \(500\) | ||||
-
この度数分布表を相対度数分布表に直してください。
-
この度数分布表を累積度数分布表に直してください。
-
この度数分布表を累積相対度数分布表に直してください。
答え
相対度数は,各階級の度数が全体に占める割合を計算すれば分かります。 累積度数は,度数を下の階級から積み上げたときの度数の合計を計算すれば分かります。 実際にやってみましょう。
-
データの大きさは\(500\)ですから,各階級の度数を\(500\)で割って相対度数を求めましょう。
階級(点) 相対度数 \(0\) 以上 ~ \(50\) 未満 \(0.006\) \(50\) ~ \(100\) \(0.016\) \(100\) ~ \(150\) \(0.03\) \(150\) ~ \(200\) \(0.072\) \(200\) ~ \(250\) \(0.122\) \(250\) ~ \(300\) \(0.202\) \(300\) ~ \(350\) \(0.324\) \(350\) ~ \(400\) \(0.162\) \(400\) ~ \(450\) \(0.052\) \(450\) ~ \(500\) \(0.014\) 計 \(1\) -
度数を下の階級から合計していけば良いです。
階級(点) 累積度数 \(50\) 未満 \(3\) \(100\) \(11\) \(150\) \(26\) \(200\) \(62\) \(250\) \(123\) \(300\) \(224\) \(350\) \(386\) \(400\) \(467\) \(450\) \(493\) \(500\) \(500\) -
相対度数を下の階級から合計していけば良いです。
階級(点) 累積相対度数 \(50\) 未満 \(0.006\) \(100\) \(0.022\) \(150\) \(0.052\) \(200\) \(0.124\) \(250\) \(0.246\) \(300\) \(0.448\) \(350\) \(0.772\) \(400\) \(0.934\) \(450\) \(0.986\) \(500\) \(1\)
