データの散らばり

はじめに

前回は代表値という，データの中心的な値を学びました。しかし，データには色々な分布のものがあり，中心を見るだけでは全体像が掴めません。今回と次回は，データの"散らばり"という情報を新しく調べてみます。

範囲

▼

データの散らばりを表す最も単純なものは範囲です。 レンジともいいます。これはデータの値がとりうる値の幅です。次のデータを見てください。

\( \begin{align} 15, \ 10, \ 7, \ 5, \ 13 \\[5pt] 21, \ 17, \ 25, \ 6, \ 8 \end{align} \)

このデータは最小で\(5\)，最大で\(25\)という値をとっています。このとき，このデータの範囲は\(25 - 5 = 20\)です。

範囲は，このようにデータのとる値の広さを表しますが，最大値・最小値しか考慮しない大雑把なものです。しかも外れ値の影響を直に受けますから，これだけでデータの散らばりを調べることはできないでしょう。

四分位数

▲

▼

データの値の最大値・最小値だけでは，範囲くらいしか考えられませんでした。そこにデータの代表値も加えて考えれば，データの両端と真ん中を把握できます。

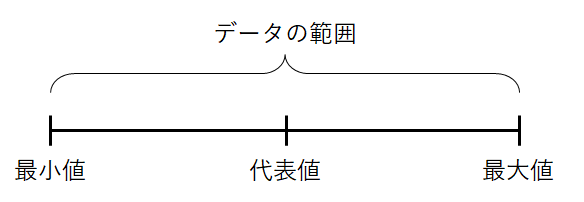
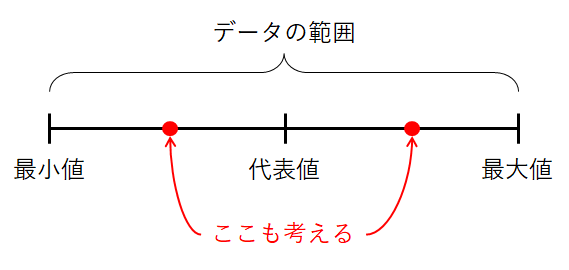
しかし両端と真ん中だけでは，まだデータの散らばり方はよく分かりません。そこで，更に真ん中と端の間の真ん中も考えることにします。つまりデータを４等分するわけです。

データの４等分は，シンプルに大きさ順に並べて行います。４等分する位置にくる値を小さい方から第１四分位数，第２四分位数，第３四分位数といいます。第２四分位数は中央値ですね。

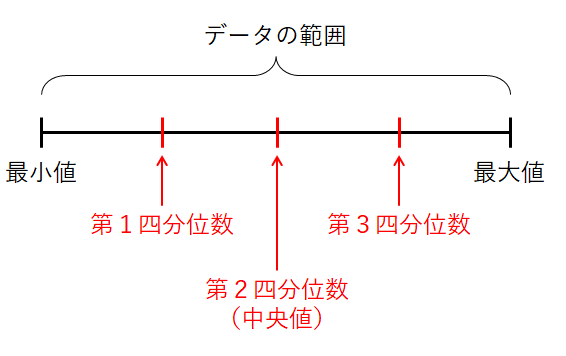
図だけ見ると勘違いしてしまうかもしれませんが，数直線上に四分位点を並べたとき，それらは等間隔に並ぶわけではありません。気を付けてください。

補足分位数

データを大きさ順に並べ替えたとき，小さい方から\(P\)％の位置にくる値を\(P\)％パーセンタイル，または\(P\)％分位数といいます。分位数は分位点ともいいます。

つまり第１四分位数は\(25\)％分位数，第２四分位数（中央値）は\(50\)％分位数，第３四分位数は\(75\)％分位数のことです。

中央値はデータを２等分する値でしたが，分位数はその拡張版で，データを色々な形で分けられます。四分位数はその具体例で，データを４等分する値なわけです。

実際に四分位数を求める練習をしましょう。四分位数の細かい定義はいくつもあり，どの定義を採用するかで四分位数の値も変わります。ここでは高校数学で採用されている定義を使います。

四分位数の求め方

四分位数は次の手順で求められる。

データを大きさ順に並び替える。
中央値（第２四分位数）を求める。
データを中央値の左グループ，右グループに分ける。
左グループの中央値（第１四分位点）を求める。
右グループの中央値（第３四分位点）を求める。

つまりデータをまず２等分し，分かれた２つのグループを更に２等分するわけです。カステラを４人で分けるときも，こうした方が綺麗に４等分できますね。具体例として，次のデータの四分位数を求めます。

\( \begin{align} 12, \ 3, \ 15, \ 6, \ 9, \ 4, \ 7 \end{align} \)

まずはこのデータを大きさ順に並べ替えます。

\( \begin{align} 3, \ 4, \ 6, \ 7, \ 9, \ 12, \ 15 \end{align} \)

次に中央値を求めます。データの大きさが\(7\)ですから，中央値（第２四分位数）は\(4\)番目の値である\(7\)ですね。

これでデータが中央値の左グループと右グループに分かれます。

\( \begin{align} \boxed{3, \ 4, \ 6}, \ 7, \ \boxed{9, \ 12, \ 15} \end{align} \)

左グループの中央値（第１四分位数）が\(4\)，右グループの中央値（第３四分位数）が\(12\)であることが分かりますね。これで四分位数が求められました。

四分位偏差

▲

▼

四分位数から次の値を定義できます。

四分位範囲と四分位偏差

データの第１四分位数，第２四分位数，第３四分位数をそれぞれ\(Q_1\)，\(Q_2\)，\(Q_3\)と表すとき，次の値を定義できる。

四分位範囲: \(Q_3-Q_1\)
四分位偏差: \(\displaystyle\frac{Q_3-Q_1}{2}\)

四分位範囲は下図の緑の範囲です。つまり，データの両端をカットしたときのデータの範囲といえます。両端をカットしたことで，外れ値の影響を排除することができ，データ全体の範囲よりもデータの散らばり具合をよく表しています。

四分位範囲の値が大きければ，それだけデータが広く散らばっているということですね。

四分位偏差は下図の緑の範囲で，四分位範囲を半分にした値です。図だと分かりづらいですが，第１四分位数と第２四分位数の間の幅ではないので注意です！四分位範囲と同じく，外れ値を排除したデータの散らばり具合を表します。

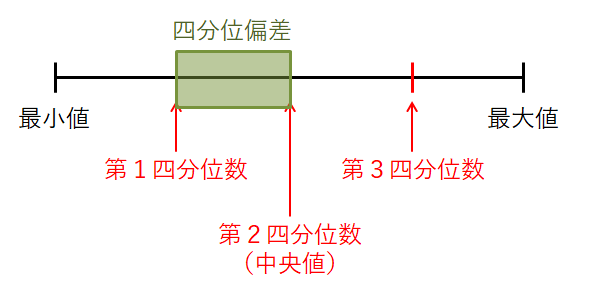
四分位範囲と四分位偏差は，ともに両端をカットしたデータを考えたものです。四分位範囲がその広がりを表すのに対して，四分位偏差は中央値とのおおよそのズレを表します。

箱ひげ図

▲

▼

四分位数の情報を図に表すために，箱ひげ図というものを使います。これはデータの最小値を\(m\)，最大値を\(M\)，第１四分位数を\(Q_1\)，第２四分位数を\(Q_2\)，第３四分位数を\(Q_3\)とするとき，これらの情報を次図のようにまとめたものです。

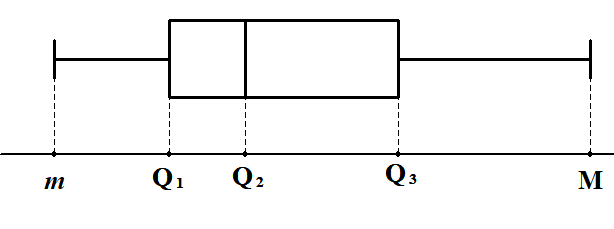
このように図にまとめると，データの分布が何となく見えてきます。四分位数はデータを４等分する点ですから，四分位数で分けられた領域にある値の個数は，どこでも同じです。データの大きさが\(100\)なら，それぞれの領域には\(25\)個の値があるわけです。

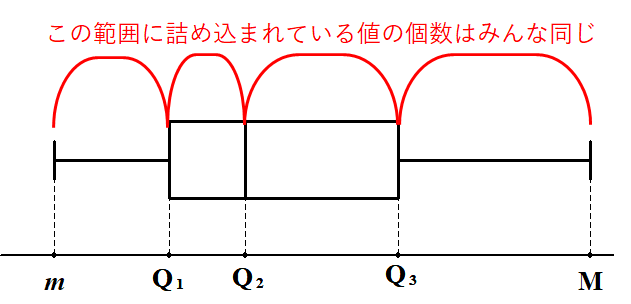
値の個数が同じなのに，領域ごとに幅が狭かったり広かったりします。つまり，幅が狭い領域にはデータが集中して存在し，幅が広い領域では広く散らばっているわけです。

データがどこに集中してどこで散らばっているか，データの"散らばり"が分かるわけですね。

補足箱ひげ図の向き

ここでは箱ひげ図を横向きに描きましたが，縦向きに描かれることもあります。その場合，下の方に小さい値，上の方に大きい値がくるように描きます。

先ほど使ったデータから箱ひげ図を描いてみましょう。

\( \begin{align} 3, \ 4, \ 6, \ 7, \ 9, \ 12, \ 15 \end{align} \)

このデータの第１四分位数は\(4\)，第２四分位数は\(7\)，第３四分位数は\(12\)ですから，箱ひげ図は次のようになります。

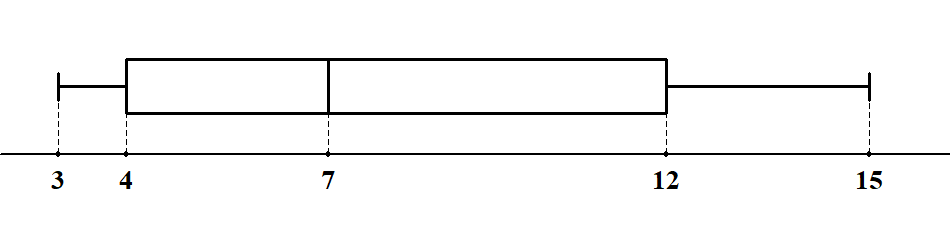
箱ひげ図から，このデータは中央値以下の部分と比べて，中央値以上の部分の方が値が散らばっていることなどが読み取れます。

ただし，この例ではデータが小さすぎて分析しがいがないですから，確認問題でもう少し大きいデータに対しても考えてみましょう。

箱ひげ図とヒストグラムの関係も考えてみます。

箱ひげ図の狭い領域の部分では，データが集中しているので，ヒストグラムの山は高くなります。箱ひげ図の広い領域の部分では，データが散らばっているので，ヒストグラムの山は低くなだらかになります。

こう考えると，箱ひげ図の情報があれば，ヒストグラムの大体の形が分かりますね。もちろん箱ひげ図の情報だけでは，ヒストグラムの完全な形までは分かりませんが，より少ない情報量でデータの分布の手掛かりになるわけですね。

確認問題

▲

次のデータについて，(1)～(3)に答えてください。

\( \begin{array}{l} 42, \ 60, \ 84, \ 27, \ 35 \\ 91, \ 35, \ 89, \ 38, \ 8 \\ 21, \ 44, \ 95, \ 37, \ 120 \\ 74, \ 48, \ 11, \ 13, \ 56 \end{array} \)

このデータの第１四分位数，第２四分位数，第３四分位数を求めてください。
このデータの四分位範囲と四分位偏差を求めてください。
このデータの箱ひげ図を描いてください。

答え

四分位数を求める練習と，箱ひげ図を描く練習が主です。

まずデータを大きさ順に並べ替えます。

\( \begin{array}{l} 8, \ 11, \ 13, \ 21, \ 27 \\ 35, \ 35, \ 37, \ 38, \ 42 \\ 44, \ 48, \ 56, \ 60, \ 74 \\ 84, \ 89, \ 91, \ 95, \ 120 \end{array} \)

このデータの大きさは\(20\)ですから，第２四分位数（中央値）は，\(10\)番目と\(11\)番目のデータの平均であり，その値は\(43\)です。また，これでデータが\(1\)番目～\(10\)番目と\(11\)番目～\(20\)番目のグループに分かれました。

第１四分位数は，前半グループの中央値であり，\(5\)番目と\(6\)番目のデータの平均ですから，その値は\(31\)です。第３四分位数は，後半グループの中央値であり，\(15\)番目と\(16\)番目のデータの平均ですから，その値は\(79\)です。

以上から，第１四分位数は\(31\)，第２四分位数は\(43\)，第３四分位数は\(79\)です。
四分位範囲は，第１四分位数と第３四分位数の間の幅ですから，\(79 - 31 = \textcolor{red}{48}\)です。四分位偏差は，四分位範囲の半分ですから，\(48 \div 2 = \textcolor{red}{24}\)です。
このデータの最小値は\(8\)，最大値は\(120\)で，四分位数は(1)で求めました。これらの情報から，このデータの箱ひげ図は次のようになります。

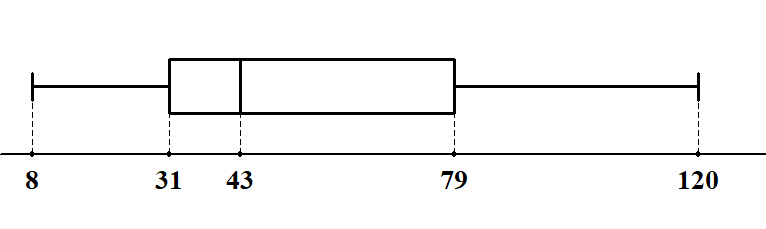
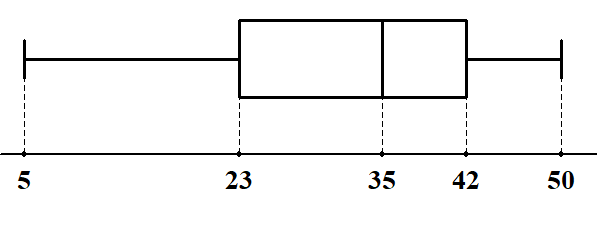
あるデータの箱ひげ図が次のようになっています。このデータについて，(1)～(3)に答えてください。

このデータの四分位偏差を求めてください。
「このデータの半数以上を\(25\)以上の値が占める」という記述が正しいかどうか答えてください。
このデータの大きさを\(11\)と仮定したとき，このデータの平均としてあり得る値の範囲を求めてください。ただし平均の値は小数第２位まで求めてください。

答え

箱ひげ図を読みとる問題です。

箱ひげ図より，第１四分位数は\(23\)，第３四分位数は\(42\)なので，四分位偏差は次のようになります。

\( \begin{align} \displaystyle\frac{42 - 23}{2} = \textcolor{red}{9.5} \end{align} \)
正しいです。箱ひげ図より，このデータの中央値は\(35\)です。中央値はこのデータを大きさ順に並べたとき，真ん中にくる値ですから，中央値以上の値はデータの半数以上を占めます。そして\(25\)以上の値は，中央値以上の値をすべて含みますから，データの半数以上を占めますね。
平均が最小になるときと最大になるときで，\(11\)個のデータの値がどうなるか考えましょう。データを次のように大きさ順で並べ，それぞれの値がどうなるか考えていきます。

箱ひげ図から分かる情報を書き込むと，次のようになります。第１～第３四分位数がそれぞれ\(3\)，\(6\)，\(9\)番目の値になることに注意しましょう。

平均が最小になるのは，この他の値がなるべく小さいときですから，次の場合です。

このときの平均は\(\displaystyle\frac{318}{11} \fallingdotseq 28.91\)です。

平均が最大になるのは，この他の値がなるべく大きいときですから，次の場合です。

このときの平均は\(\displaystyle\frac{382}{11} \fallingdotseq 34.73\)です。

以上から，平均としてありえる値の範囲は，\(28.91\)以上\(34.73\)以下です。