これまでは1つのデータの分布を考えてきました。 今回は2つのデータのペアを考えて,それらの間の関係を考えていきます。
目次
散布図
今までは1つの変量について考えてきました。 例えば,あるグループにいる人の身長などです。 今回はもう1つ変量を考えて,それらの間の関係を考えてみます。
今の例では,あるグループの身長だけを測定しましたが,さらに体重も測定して,身長と体重の関係を考えることにしましょう。 このとき,身長\(x\),体重\(y\)という2つの変量を考えることになります。
\(x\),\(y\)のデータの値を次のように表します。
これらの間の関係を考えるとき,散布図を描くと視覚的に特徴を捉えやすいです。 散布図は,データの値のペアを座標平面上の点として描いたものです。
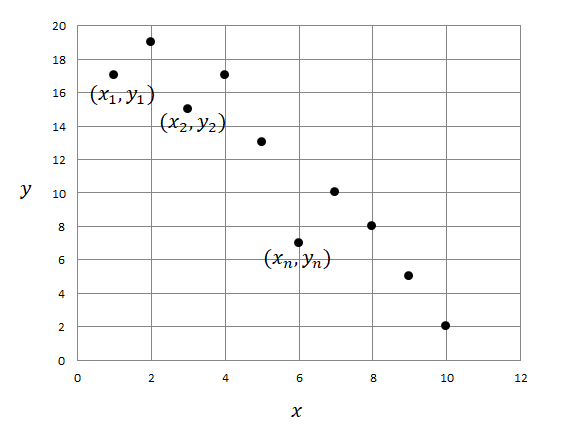
具体例を見てみます。 ある\(10\)人の身長\(x\),体重\(y\)のデータが次の通りだったとします。
| 番号 | 身長\(x\)[\(\mathrm{cm}\)] | 体重\(y\)[\(\mathrm{kg}\)] |
|---|---|---|
| \(1\) | \(163\) | \(61\) |
| \(2\) | \(172\) | \(59\) |
| \(3\) | \(165\) | \(56\) |
| \(4\) | \(158\) | \(51\) |
| \(5\) | \(163\) | \(58\) |
| \(6\) | \(155\) | \(49\) |
| \(7\) | \(176\) | \(70\) |
| \(8\) | \(180\) | \(75\) |
| \(9\) | \(172\) | \(62\) |
| \(10\) | \(161\) | \(58\) |
このデータから散布図を描くと次のようになります。
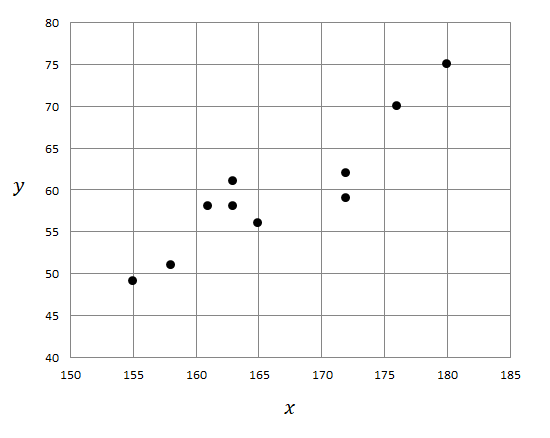
散布図を描くと何となくデータの傾向が見えてきますね。 身長が高いと体重も重くなる傾向が見えます。
相関関係
2変量\(x\),\(y\)の関係を見るとき,これらの間に区別を設けず対等に見る方法を相関といいます。 片方からもう一方が決まるという見方をするときは回帰といいます。
ここで考えるのは主に相関関係です。 相関関係には,次の3種類が考えられます。 散布図から判断できるようにしましょう。
【1】 まず正の相関関係があります。 これは一方の変量が増えると他方の変量も増える場合です。 散布図で見ると,データの点が全体的に右上がりの直線状に分布しています。
先ほど見た身長と体重の間には,正の相関関係があるといえそうですね。

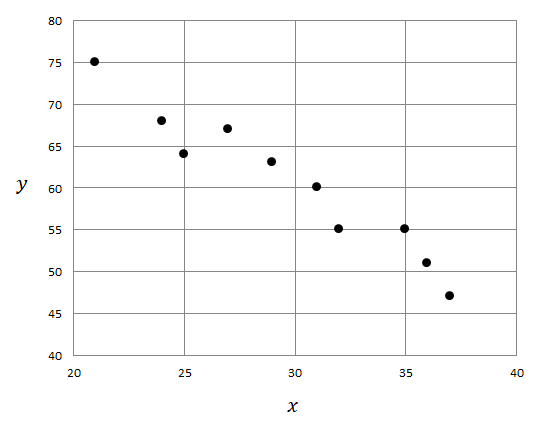
【2】 また負の相関関係もあります。 これは一方の変量が増えると他方の変量は減る場合です。 散布図で見ると,データの点が全体的に右下がりの直線状に分布しています。
日中の平均気温を\(x\)[\(\mathrm{C^{\circ}}\)],街中で見かけた長袖の服を着た人の数を\(y\)[人]とすると,これらの変量は次の散布図のような負の相関関係を持ちそうです。
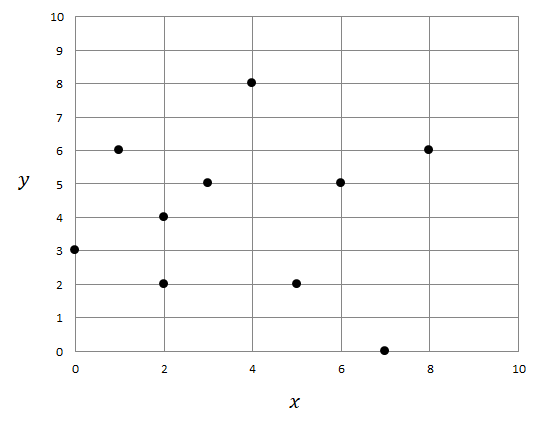
【3】 他に相関関係がない場合もあります。 これは正の相関関係も負の相関関係も見られない場合です。 散布図で見ると,データの点が直線状に分布しておらず,散らばっています。
ある人が\(10\)回のじゃんけんで勝った回数を\(x\)[回],\(1\)年間で旅行に行った回数を\(y\)[回]とすると,これらの変量は次の散布図のように相関関係がなさそうです。
2変量の間に相関関係が見られる場合でも,それらの間に因果関係があるとは限りません。 因果関係とは,一方の変量が「原因」となって,もう一方の変量がその「結果」として決まるという関係です。
例えば,身長と体重に正の相関関係があることを見ましたが,ここに因果関係はありません。 単に身長が高ければ体重も重い傾向にあり,体重が重ければ身長も高い傾向にあるというだけで,一方がもう一方を決定するとは言えないからです。
また因果関係があっても,ここで説明したような相関関係があるとも限りません。 因果関係には直線的な関係だけでなく,もっと複雑な関係もあるからです。
このように相関関係と因果関係は簡単には結び付けられません。 これを正しく見極めるのは難しいですが,誤った判断をしてしまわないよう意識しておきたいことです。
共分散
散布図から相関関係を視覚的に判断しましたが,客観性が足りません。 また視覚的情報だけでは,相関関係の強さを比べることも難しいですね。 もっと客観的に相関関係を判断できるよう計算することを考えましょう。
2変量\(x\),\(y\)のデータの値を次のように表します。 またそれぞれの平均を\(\overline{x}\),\(\overline{y}\)と表します。
それぞれの偏差の積を偏差積といい,これが相関関係を調べるのに役立ちます。 例えば次の式が,データの1つめの値の偏差積です。
偏差積が正であるとき,2つの偏差は同符号です。 つまり一方が平均より大きいとき他方も平均より大きく,一方が平均より小さいとき他方も平均より小さいことを表します。 これは正の相関関係の傾向です。
偏差積が負であるとき,2つの偏差は異符号です。 つまり一方が平均より大きいとき他方は平均より小さいことを表します。 これは負の相関関係の傾向です。
このことから,偏差積の平均をとれば,全体的な相関関係が見えてきそうですね。 これを共分散といいます。
変量\(x\),\(y\)の共分散\(s_{xy}\)は次の式で定義される。
共分散が正なら,全体的に正の相関関係があることが,共分散が負なら,全体的に負の相関関係があることが分かります。 これで相関関係を計算できるようになりました。
相関係数
共分散には,相関関係の強さまでは表せない弱点があります。 一見,共分散の絶対値が大きければ相関関係も強そうに思えます。 例えば正の相関関係が強ければ,偏差積の多くが正になり,共分散は大きくなりそうです。
しかし,共分散の式を見れば分かる通り,データのバラつきが大きいだけでも共分散は大きくなってしまいます。 なので共分散が大きいからといって相関関係が強いとは限らないのです。
この問題の修正のため,共分散を変量の標準偏差で割ったのが相関係数です。
変量\(x\),\(y\)の共分散を\(s_{xy}\),それぞれの標準偏差を\(s_x\),\(s_y\)とすると,相関係数\(r\)は次の式で定義される。
相関係数は,共分散を標準偏差で割ることで,バラつきの影響をなくしています。 また,相関係数は無単位になりますから,単位のスケールによる影響も排除しています。
変量\(x\),\(y\)の単位をそれぞれ\(\mathrm{u}_x\),\(\mathrm{u}_y\)とします。 共分散\(s_{xy}\)は,変量の偏差積の和ですから,その単位は\(\mathrm{u}_x\mathrm{u}_y\)です。 また\(x\),\(y\)の標準偏差\(s_x\),\(s_y\)の単位は,以前見たようにそれぞれ\(\mathrm{u}_x\),\(\mathrm{u}_y\)です。
したがって相関係数は,次のように無単位になります。
実際,共分散を標準偏差で割るという調整によって,相関係数のとる値の範囲は次のようになります。 本当にそうなることは,確認問題で見ることにします。
相関係数は,共分散のように相関関係を表すだけでなく,その強弱まで表します。 つまり\(1\)に近いほど強い正の相関関係が,\(-1\)に近いほど強い負の相関関係があることを表します。 \(0\)に近ければ相関関係はありません。
バラつきやスケールの影響を排除したことで,相関係数の絶対値の大きさは,そのまま相関関係の傾向の強さを表せるようになったわけです。
相関係数を使えば,相関関係の強さの比較ができます。 しかし,相関係数の値だけ見ても,相関関係の具体的な強さはあまりはっきりしません。
例えば相関係数が\(0.5\)のとき,何となくそこそこの相関関係がありそうに思えますが,実際には散布図を見ても相関関係を認識しづらいくらいです。
相関係数は比較には使えますが,その値だけで相関関係の強さを知るのは難しいです。 散布図を使った確認もした方が良さそうですね。
確認問題
次の2変量\(x\),\(y\)のデータについて,次の問いに答えてください。 計算は小数第2位まで行ってください。
| 番号 | \(x\) | \(y\) |
|---|---|---|
| \(1\) | \(25\) | \(7\) |
| \(2\) | \(48\) | \(4\) |
| \(3\) | \(22\) | \(8\) |
| \(4\) | \(39\) | \(7\) |
| \(5\) | \(34\) | \(6\) |
| \(6\) | \(43\) | \(4\) |
| \(7\) | \(45\) | \(2\) |
| \(8\) | \(23\) | \(9\) |
| \(9\) | \(40\) | \(5\) |
| \(10\) | \(31\) | \(8\) |
-
\(x\)を横軸,\(y\)を縦軸とした散布図を描いてください。
-
\(x\),\(y\)に相関関係があるかどうか答えてください。また,相関関係がある場合は,それが正負のどちらであるかも答えてください。
-
\(x\),\(y\)の共分散を求めてください。
-
\(x\),\(y\)の相関係数を求めてください。
答え
学んだことをひとつずつ実践していきましょう。
-
座標平面上に点を描くだけです。
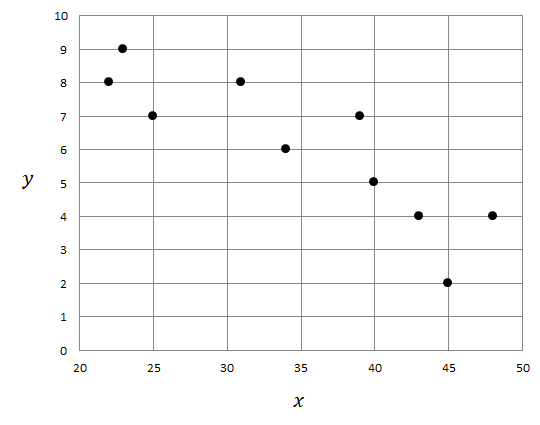
-
散布図から,負の相関関係があることが分かります。
-
共分散を\(s_{xy}\)とします。 共分散を求めるには,偏差積の和を求める必要があります。 まずは変量\(x\),\(y\)の平均\(\overline{x}\),\(\overline{y}\)を求めましょう。
\( \begin{align} \overline{x} &= \displaystyle\frac{25 + 48 + \cdots + 31}{10} \\[5pt] &= \displaystyle\frac{350}{10} \\[5pt] &= 35 \\[5pt] \overline{y} &= \displaystyle\frac{7 + 4 + \cdots + 8}{10} \\[5pt] &= \displaystyle\frac{60}{10} \\[5pt] &= 6 \\[5pt] \end{align} \)平均が分かったので,偏差と偏差積も求められます。
番号 \(x - \overline{x}\) \(y - \overline{y}\) 偏差積 \(1\) \(-10\) \(1\) \(-10\) \(2\) \(13\) \(-2\) \(-26\) \(3\) \(-13\) \(2\) \(-26\) \(4\) \(4\) \(1\) \(4\) \(5\) \(-1\) \(0\) \(0\) \(6\) \(8\) \(-2\) \(-16\) \(7\) \(10\) \(-4\) \(-40\) \(8\) \(-12\) \(3\) \(-36\) \(9\) \(5\) \(-1\) \(-5\) \(10\) \(-4\) \(2\) \(-8\) 共分散はこの偏差積の平均ですね。
\( \begin{align} s_{xy} &= \displaystyle\frac{(-10) + (-26) + \cdots + (-8)}{10} \\[5pt] &= -\displaystyle\frac{163}{10} \\[5pt] &= \textcolor{red}{-16.3} \end{align} \)共分散が負ですから,散布図の見た目通り,\(x\),\(y\)には負の相関関係があることが分かります。
-
相関係数を\(r\)とします。 相関係数は共分散を標準偏差で割ったものです。 \(x\),\(y\)の標準偏差\(s_x\),\(s_y\)を求めます。 偏差は(3)で求めましたから,その2乗もすぐ求められます。
番号 \((x - \overline{x})^2\) \((y - \overline{y})^2\) \(1\) \(100\) \(1\) \(2\) \(169\) \(4\) \(3\) \(169\) \(4\) \(4\) \(16\) \(1\) \(5\) \(1\) \(0\) \(6\) \(64\) \(4\) \(7\) \(100\) \(16\) \(8\) \(144\) \(9\) \(9\) \(25\) \(1\) \(10\) \(16\) \(4\) これでまず分散を求められます。
\( \begin{align} {s_x}^2 &= \displaystyle\frac{100 + 169 + \cdots + 16}{10} \\[5pt] &= \displaystyle\frac{804}{10} \\[5pt] &= 80.4 \\[5pt] {s_y}^2 &= \displaystyle\frac{1 + 4 + \cdots + 4}{10} \\[5pt] &= \displaystyle\frac{44}{10} \\[5pt] &= 4.4 \\[5pt] \end{align} \)分散の正の平方根が標準偏差ですから,相関係数は次のように求められます。
\( \begin{align} r &= \displaystyle\frac{s_{xy}}{s_xs_y} \\[5pt] &= -\displaystyle\frac{16.3}{\sqrt{80.4}\sqrt{4.4}} \\[5pt] &= -\displaystyle\frac{16.3\sqrt{80.4}\sqrt{4.4}}{80.4 \times 4.4} \\[5pt] &= \textcolor{red}{-0.87} \end{align} \)相関係数の値は\(-1\)に近く,なかなか強い負の相関関係がありますね。 実際,散布図を見ても直線的な関係がはっきりしています。
\(a_1, a_2, \cdots, a_n, b_1, b_2, \cdots, b_n\)を実数とします。 また\(X\),\(Y\),\(Z\)を次のように定義します。
-
次の\(t\)の2次関数\(f(t)\)が常に\(0\)以上であることを証明してください。
\( \begin{align} f(t) = Yt^2 - 2Xt + Z \end{align} \) -
次の不等式を証明してください。 これをコーシー・シュワルツの不等式といいます。
\( \begin{align} X^2 \leqq YZ \end{align} \) -
コーシー・シュワルツの不等式を利用して,相関係数\(r\)が次の不等式を満たすことを証明してください。
\( \begin{align} -1 \leqq r \leqq 1 \end{align} \)
答え
相関係数のとる値の範囲を証明する問題です。 ヒントなしで証明するのは難しいかもしれませんが,(1)~(3)の順に追えば証明できます。
-
\(Yt^2\),\(-2Xt\),\(Z\)を展開すると,これらの\(i\)番目の項はそれぞれ次のようになります。
\( \begin{align} {a_i}^2t^2, \ -2a_ib_it, \ {b_i}^2 \end{align} \)\(f(t)\)をこれらの項ごとにまとめると,\(i\)番目の項は次のようになります。
\( \begin{align} {a_i}^2t^2 -2a_ib_it + {b_i}^2 = (a_it - b_i)^2 \end{align} \)したがって,\(f(t)\)は次のように2乗の項の和となり,常に\(0\)以上であることが分かります。
\( \begin{align} f(t) &= (a_1t - b_1)^2 + (a_2t - b_2)^2 + \cdots + (a_nt - b_n)^2 \\[5pt] &\geqq 0 \end{align} \) -
\(Y > 0\)のとき,\(f(t)\)のグラフは下に凸の放物線ですから,これが常に\(0\)以上ということは,グラフと\(t\)軸の共有点は\(1\)個以下です。 したがって,\(f(t)\)の判別式を\(D\)とすると,次が成り立ちます。
\( \begin{align} \displaystyle\frac{D}{4} = X^2 - YZ \leqq 0 \\[5pt] \end{align} \)これを変形すると,題意の不等式が成り立つことが分かります。
\( \begin{align} X^2 \leqq YZ \end{align} \)また,\(Y\)は2乗の項の和であり\(0\)以上ですから,\(Y = 0\)の場合も検討する必要があります。 このとき,\(Y\)の項\({a_i}^2\)がひとつでも正なら\(Y > 0\)になってしまいますから,次が成り立ちます。
\( \begin{align} a_1 = a_2 = \cdots = a_n = 0 \end{align} \)したがって,\(X = 0\)も成り立ち,この場合も\(X^2 \leqq YZ\)が成り立ちます。
-
相関係数の不等式とコーシー・シュワルツの不等式を見比べると,方針が定まります。 まず相関係数の式を確認しておきましょう。 変量\(x\),\(y\)の共分散を\(s_{xy}\),標準偏差をそれぞれ\(s_x\),\(s_y\)とすると,相関係数\(r\)は次の式で表されます。
\( \begin{align} r = \displaystyle\frac{s_{xy}}{s_xs_y} \end{align} \)また\(s_{xy}\),\(s_x\),\(s_y\)は,\(x\),\(y\)の平均をそれぞれ\(\overline{x}\),\(\overline{y}\)とすると,次の式で表されます。
\( \begin{align} s_{xy} = \displaystyle\frac{(x_1 - \overline{x})(y_1 - \overline{y}) + \cdots + (x_n - \overline{x})(y_n - \overline{y})}{n} \end{align} \)\( \begin{align} {s_x}^2 = \displaystyle\frac{(x_1 - \overline{x})^2 + \cdots + (x_n - \overline{x})^2}{n} \end{align} \)\( \begin{align} {s_y}^2 = \displaystyle\frac{(y_1 - \overline{y})^2 + \cdots + (y_n - \overline{y})^2}{n} \end{align} \)この式とコーシー・シュワルツの不等式を見比べると,\(a_i\),\(b_i\)に次の式を当てはめることで,相関係数に結び付けられそうです。
\( \begin{align} a_i &= x_i - \overline{x} \\[5pt] b_i &= y_i - \overline{y} \end{align} \)このとき,\(X\),\(Y\),\(Z\)は次のようになります。
\( \begin{align} X &= (x_1 - \overline{x})(y_1 - \overline{y}) + \cdots + (x_n - \overline{x})(y_n - \overline{y}) \\[5pt] &= ns_{xy} \end{align} \)\( \begin{align} Y &= (x_1 - \overline{x})^2 + \cdots + (x_n - \overline{x})^2 \\[5pt] &= n{s_x}^2 \end{align} \)\( \begin{align} Y &= (y_1 - \overline{y})^2 + \cdots + (y_n - \overline{y})^2 \\[5pt] &= n{s_y}^2 \end{align} \)これをコーシー・シュワルツの不等式に当てはめると,次のようになります。
\( \begin{align} (ns_{xy})^2 &\leqq (n{s_x}^2) \cdot (n{s_y}^2) \\[5pt] n^2{s_{xy}}^2 &\leqq n^2{s_x}^2{s_y}^2 \\[5pt] {s_{xy}}^2 &\leqq {s_x}^2{s_y}^2 \\[5pt] \displaystyle\frac{{s_{xy}}^2}{{s_x}^2{s_y}^2} &\leqq 1 \\[5pt] \left(\displaystyle\frac{s_{xy}}{s_xs_y}\right)^2 &\leqq 1 \\[5pt] r^2 &\leqq 1 \\[5pt] \end{align} \)したがって,題意の不等式が成り立ちます。
\( \begin{align} -1 \leqq r \leqq 1 \end{align} \)
