目次

• 関数と変数
• 方程式と未知数
• 定数
• 確認問題

関数と変数

関数はある種の機械のようなものです。下の図を見てください。 関数には材料の投入口と製品の排出口があり，材料を加工して製品をつくります。 この投入口と排出口のことを変数といいます。 投入口が複数ある関数もありますが，排出口はどの関数にも１つしかありません。

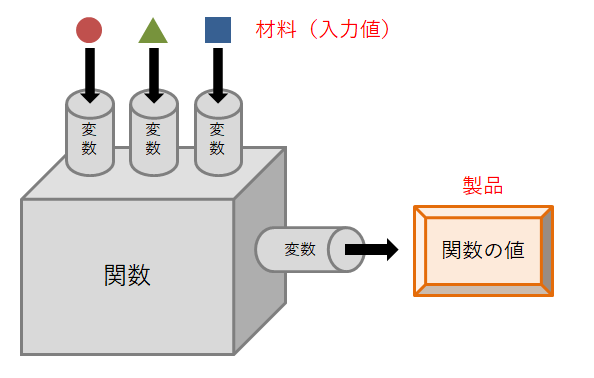
数学なので投入口に入れる材料は何らかの数です。これを加工して１つの新しい値（製品）をつくるのが関数のはたらきです。

この関数・変数に名前を付けてあげれば，数式で表現できます。 例えば下図のように関数・変数に名前を付けたとしましょう。

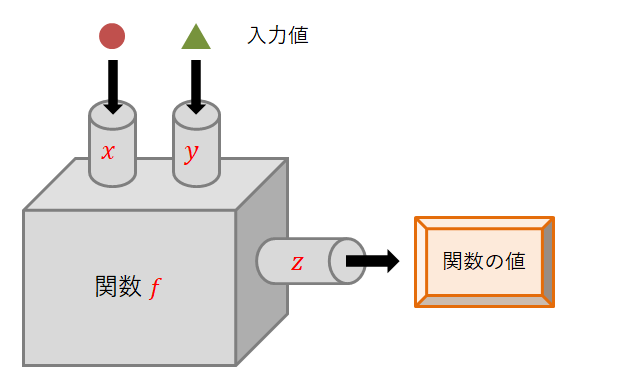
これを数式で\(z = f(x, y)\)と表します。 \(f\)が関数名で\(x, \ y, \ z\)が変数名です。 \(()\)の中は投入口を表し，関数\(f\)には\(x, \ y\)という２つの投入口があります。 また，関数が排出口から出す値に\(z\)と名前を付けています。

\(f(x, y)\)という関数は投入された\(x, y\)を加工するわけですから， 例えば\(f(x, y) = x^2 + xy\)のように，具体的な形は\(x, y\)の式になります。 この計算式で\(x, y\)を組み合わせた新しい値をつくるわけです。

また見方を変えると，関数は\(z = x^2 + xy\)のように， いくつかの変数の間の関係を表した式と捉えることもできます。

方程式と未知数

関数の説明で\(z = x^2 + xy\)という関係式が出てきました。 これは単なる関係式である一方，変数\(x, \ y, \ z\)に対する制約とも捉えられます。

つまり\(x, \ y, \ z\)はどんな値でも良いわけではなく，常にこの関係式を満たすように制限をかけられているのです。 例えば\(y = 2, \ z = 3\)のときは\(x = 1\)か\(x = -3\)でなければなりません。 \(x\)がそれ以外の値をとると関係式を満たせなくなってしまうからです。

このように変数間の制約を表した等式が方程式です。 方程式ではその式を満たす変数にどんな値があり得るのかを調べます。 方程式として考えるとき，この調べたい変数を未知数と呼びます。

関数は材料の数を入れると新しい値をつくってくれるものでした。 関数について調べるときには，その関数がどんな値をつくる機械なのかという関数の性質に最も興味があります。

それに対して方程式を考えるときは，関数そのものが興味の対象ではありません。 その関数を使って目当ての値をつくるにはどんな材料が必要かを考えます。

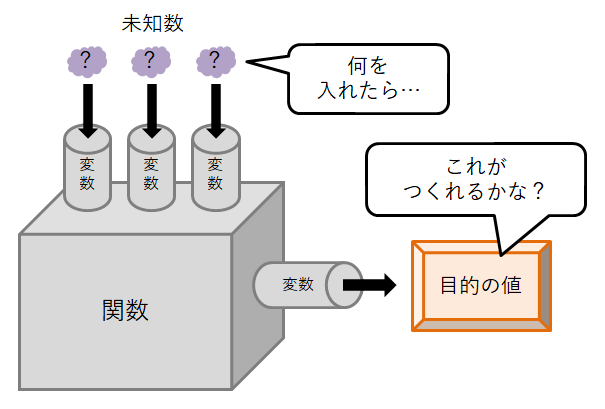
例えば\(x^2 + 4x + 3 = 0\)という方程式は， \(y = x^2 + 4x + 3\)という関数を使って\(0\)という値をつくりたいとき， どんな\(x\)を関数に与えればよいかという問題なのです。

このように方程式と関数は密接に関わりあっています。 関数そのものに対する理解があれば方程式が解きやすくなりますし， 方程式の解法を心得ていれば関数の性質を知るのに役立ちます。

定数

\(y = x^2 + ax + 3\)という関数で\(a\)を定数としましょう。 この\(a\)は一体どんなものなのでしょうか。

定数は値が固定され変化しない数です。 しかし\(a\)は\(1\)かもしれないし，\(2\)かもしれません。 定数の値も色々ありえるということで，定数と変数って何が違うの？と混乱しがちなところです。

今までの例え話を使うと，変数は関数という機械の投入口・排出口でした。 それに対し，定数とは機械のカスタマイズ用パーツなのです。

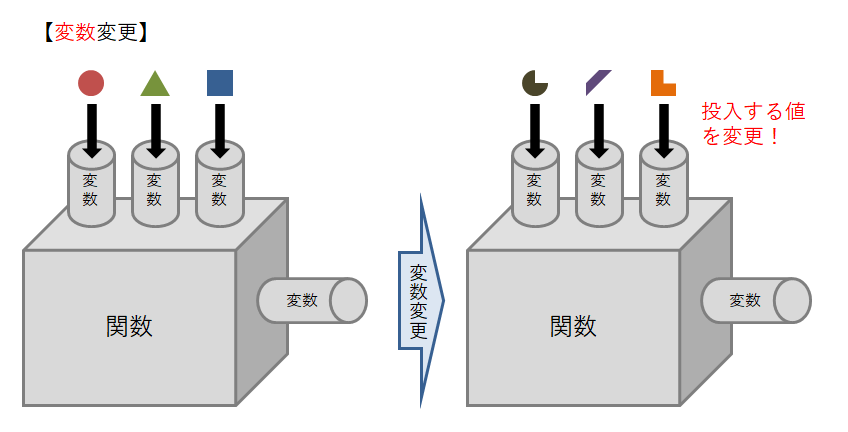
つまり定数の値を変更すると，関数そのものを違う動きをするように変更できます。 それに対し，変数を変更するということは単に機械に投入する材料を変えているだけなのです。

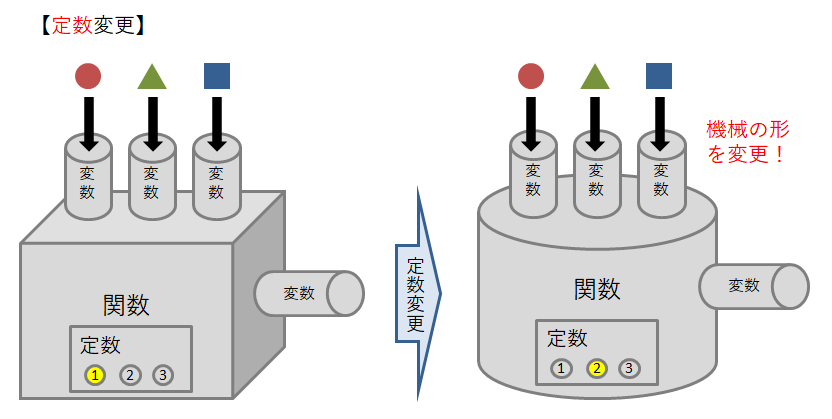
例えば「１次関数の\(x\)の係数って関数の性質にどう影響するんだろう？」と考えるとき， \(x\)の係数の値をいろいろにカスタマイズできる１次関数を用意すると便利です。 そこで\(x\)の係数を定数\(a\)で表した\(y = ax\)という関数をつくって調べたりするわけです。

確認問題