集合の要素の数え方を学びます。 今後,場合の数や確率を求めるのに役立つ内容です。 集合についての知識はこちらから学習できます。
目次
和集合の要素数
集合\(A\)の要素の個数を次のように表すことにします。
これから全体集合を\(U\)とする集合\(A\),\(B\)を考えていきます。 和集合\(A \cup B\)の要素の個数はどうなるでしょうか?
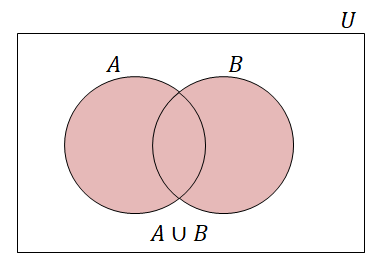
仮に\(n(A)\)と\(n(B)\)をそのまま足すと,\(A \cap B\)の要素を2回カウントすることになります。 なので,そこから\(n(A \cap B)\)を引けばちょうど\(n(A \cup B)\)になります。
和集合\(A \cup B\)の要素の個数は次の式で求められる。
このように,集合の要素数を数えるときは,思い切って各集合の要素数を足してしまって,後から重複してカウントした分を調整します。 場合の数を求めるときも同じ考え方です。
ちなみに,上の式を変形すれば,和集合の要素数から共通部分の要素数を求める公式になります。 しかし,大抵は共通部分の方が要素数を求めやすいので,上の形の公式を使うことになります。
補集合の要素数
次は補集合の要素の個数を考えてみましょう。
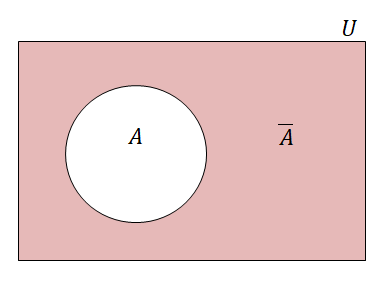
これはベン図を見れば明らか,というか見なくても明らかですね。
補集合\(\overline{A}\)の要素の個数は次の式で求められる。
ベン図と要素数
和集合や補集合の要素数を求める公式を確認してきましたが,ベン図で要素数を整理する方法も学びましょう。 ベン図に要素数を書き込むだけですが,かなり便利です。
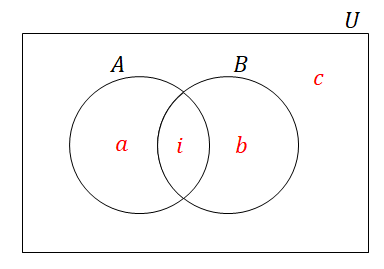
上図には,ベン図の線で囲まれた各部分の要素数を書き込んでいます。 \(a = n(A)\),\(b = n(B)\)ではないので注意してください。
具体的には,図の\(a\),\(b\),\(i\),\(c\)は次の要素数です。
ちなみに,\(i\)はintersection(共通部分),\(c\)はcomplement(補集合)の頭文字として使いました。
このようにベン図に要素数を書き込んでおくと,例えば\(\overline{A} \cup B\)のようなピンとこない集合の要素数もすぐ分かります。 この集合はベン図では次の部分ですね。
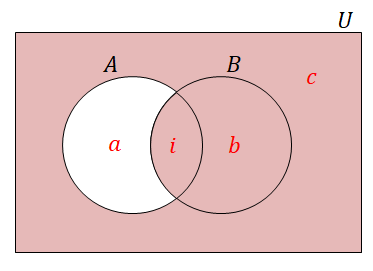
ベン図を見ればすぐ分かる通り,\(\overline{A} \cup B\)の要素数は次のようになります。
公式だけに頼ると柔軟に色々な集合に対応できません。 ベン図で確認することを基本にしましょう。
数え方の注意
集合の要素数を数えるとき,よく間違われる点について注意しておきます。 次の集合の要素数はいくつでしょうか?
\(n(A)\)は\(53\)以上\(87\)以下の整数の個数ですが,よく次の計算をする人がいます。
残念ながらこれは間違いです。 正しくは次の計算で\(n(A)\)を求めます。
最後に\(1\)を足す必要があるんですね。 \(87\)から\(53\)を引いてしまうと,\(53\)という数も数えなくなってしまいます。 だから\(53\)も数えるために,最後に\(1\)を足すのです。
別の考え方もあります。 \(53\)から\(87\)までの数を数えたいのですから,\(53\)の手前の\(52\)までの数を数えないようにしたいわけです。 なので,\(n(A)\)は次の計算で求められます。
結果的には同じ事ですが,腑に落ちやすい方で理解しておいてください。
確認問題
\(794\)以上\(1185\)以下の整数全体の集合を全体集合とします。 次の問いに答えてください。
-
\(5\)の倍数の個数を答えてください。
-
\(7\)の倍数の個数を答えてください。
-
\(5\)の倍数かつ\(7\)の倍数である数の個数を答えてください。
-
\(5\)の倍数または\(7\)の倍数である数の個数を答えてください。
-
\(5\)の倍数であるが\(7\)の倍数ではない数の個数を答えてください。
-
\(5\)の倍数でも\(7\)の倍数でもない数の個数を答えてください。
答え
全体集合を\(U\)とし,全体集合の中で\(5\)の倍数全体の集合を\(A\),\(7\)の倍数全体の集合を\(B\)とします。 ベン図に要素数を書き込みながら情報を整理します。
-
\(U\)の中で最小の\(5\)の倍数は\(795 = 5 \cdot 159\),最大の\(5\)の倍数は\(1185 = 5 \cdot 237\)ですから,\(A\)は次の集合です。
\( \begin{align} A = \{5 \cdot 159,\ 5 \cdot 160,\ \cdots,\ 5 \cdot 237\} \end{align} \)したがって,\(n(A)\)は次のように求められます。
\( \begin{align} n(A) = 237 - 159 + 1 = \textcolor{red}{79} \end{align} \)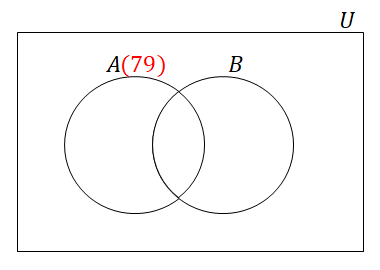
-
\(U\)の中で最小の\(7\)の倍数は\(798 = 7 \cdot 114\),最大の\(7\)の倍数は\(1183 = 7 \cdot 169\)ですから,\(B\)は次の集合です。
\( \begin{align} B = \{7 \cdot 114,\ 7 \cdot 115,\ \cdots,\ 7 \cdot 169\} \end{align} \)したがって,\(n(B)\)は次のように求められます。
\( \begin{align} n(B) = 169 - 114 + 1 = \textcolor{red}{56} \end{align} \)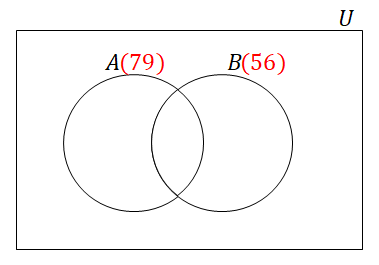
-
\(5\)の倍数かつ\(7\)の倍数である数とは,\(35\)の倍数のことです。 \(U\)の中で最小の\(35\)の倍数は\(805 = 35 \cdot 23\),最大の\(35\)の倍数は\(1155 = 35 \cdot 33\)ですから,\(A \cap B\)は次の集合です。
\( \begin{align} A \cap B = \{35 \cdot 23,\ 35 \cdot 24,\ \cdots,\ 35 \cdot 33\} \end{align} \)したがって,\(n(A \cap B)\)は次のように求められます。
\( \begin{align} n(A \cap B) = 33 - 23 + 1 = \textcolor{red}{11} \end{align} \)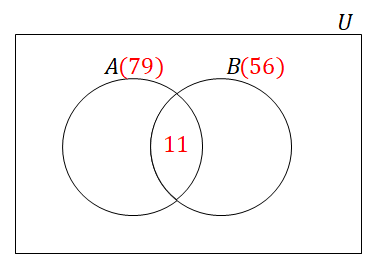
-
公式を使って計算できます。
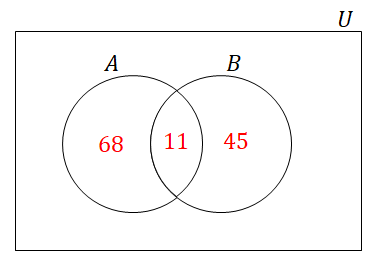
\( \begin{align} n(A \cup B) &= n(A) + n(B) - n(A \cap B) \\[5pt] &= 79 + 56 - 11 \\[5pt] &= \textcolor{red}{124} \end{align} \)ベン図に書き込む要素数を整理すると次のようになりますから,この図から要素数の合計を計算しても良いです。
-
\(n(A \cap \overline{B})\)を求めるわけですが,\(A \cap \overline{B}\)はベン図では次の部分です。
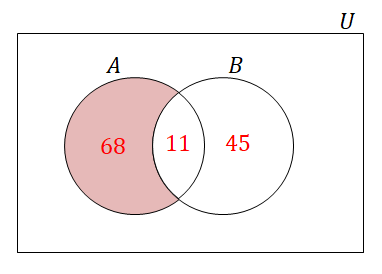
ベン図から分かる通り,\(n(A \cap \overline{B}) = 68\)です。
-
\(A \cup B\)の補集合の要素数を求めれば良いですね。 まず全体集合の要素数を求めておきます。
\( \begin{align} n(U) = 1185 - 794 + 1 = 392 \end{align} \)これで\(n(\overline{A \cup B})\)を求められます。
\( \begin{align} n(\overline{A \cup B}) &= n(U) - n(A \cup B) \\[5pt] &= 392 - 124 \\[5pt] &= \textcolor{red}{268} \end{align} \)
