前回に引き続き,今回も集合の要素を数えます。 今回は3集合を同時に考えますが,基本的な考え方は2集合の場合と変わりません。
目次
和集合の要素数
3つの集合\(A\),\(B\),\(C\)を考えます。 これらの和集合の要素数はどうなるでしょうか?
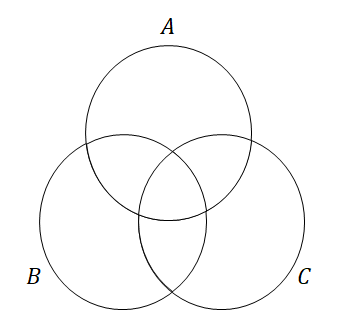
まずは思い切って\(n(A)\),\(n(B)\),\(n(C)\)を全部足してしまいましょう。 その後で重複して数えた部分を調整します。
いま各部分を何回カウントしたか,ベン図にカウントした回数分だけ点を打って確認してみましょう。 例えば\(n(A)\)でカウントされるのは次の部分です。
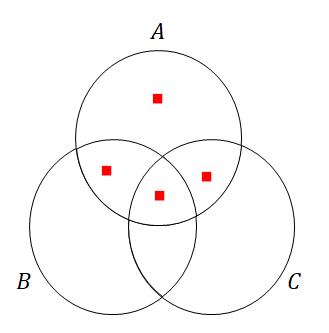
同様に点を打っていくと,次のようになります。
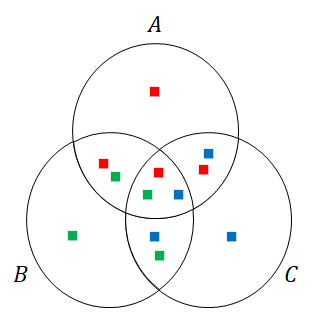
この図を見ると,ベン図の真ん中の方で2~3回カウントしてしまっていることが分かります。 重複分の調整のため,次は\(A \cap B\),\(B \cap C\),\(C \cap A\)の要素数を引きます。
\(A \cap B \cap C\)の分の調整はまた後で行います。 大きな集合で大雑把に計算してから,小さな集合で調整するのが基本です。
先ほどベン図に打った点をこの調整の分だけ減らしてみます。
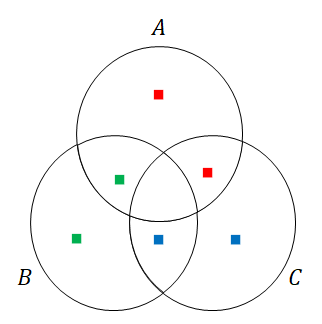
この図を見ると,あとは\(A \cap B \cap C\)の要素数を足せば完成だと分かりますね!
和集合\(A \cup B \cup C\)の要素の個数は次の式で求められる。
なかなか長い式ですが,結構使います。 まず大きな集合を足してしまって,次に2集合ずつの共通部分を引いて調整し,最後に3集合の共通部分を足して再調整しています。 調整に調整を重ねたものと考えれば,覚えやすいと思います。
基本はベン図
集合がいくつあっても,ベン図に要素数を書き込んで情報を整理すると便利です。 3集合のベン図では,要素数を書き込む箇所が7箇所ありますね。
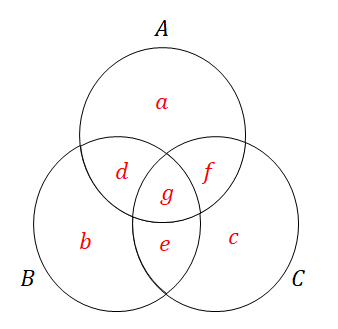
それぞれの部分の要素数は,小さい集合から順に特定していくことになります。 例えば,次の情報が分かっているとしましょう。
このとき,先ほどのベン図の\(a\)を求めてみましょう。 まず\(g\)は分かっていますね。
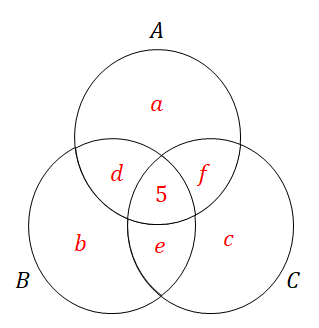
次に\(d\)と\(f\)も分かります。 \(g = 5\)であることを活用します。
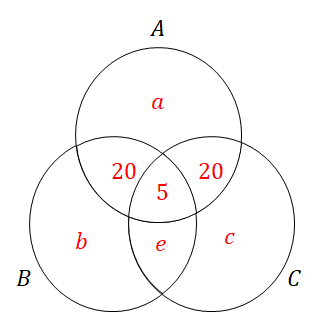
ここまで情報が揃えば\(a\)も分かります。
このようにベン図の各部分の要素数を特定していけば,\(A \cap (B \cup C)\)のようなピンとこない集合の要素数もすぐ分かります。 この集合は\(A\)の中で\(B\)または\(C\)でもある部分ですから,ベン図では次の部分です。
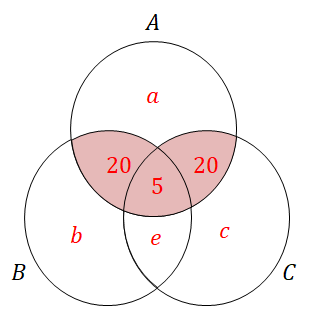
したがって,\(A \cap (B \cup C)\)の要素数は次のようになります。
2集合の和集合の要素数を求める計算を思い出すと,上の要素数は次の計算でも求められます。
大雑把に足してから細かく調整する方法ですね。
確認問題
\(794\)以上\(1185\)以下の整数全体の集合\(U\)を全体集合とします。 また,\(U\)の中で\(k\)の倍数全体の集合を\(S_k\)と表し,集合\(X\)の要素の個数を\(n(X)\)と表します。 次の問いに答えてください。
-
\(n(S_3)\),\(n(S_5)\),\(n(S_7)\)を求めてください。
-
\(n(S_3 \cap S_5)\),\(n(S_5 \cap S_7)\),\(n(S_7 \cap S_3)\)を求めてください。
-
\(n(S_3 \cap S_5 \cap S_7)\)を求めてください。
-
\(n(S_3 \cup S_5 \cup S_7)\)を求めてください。
-
\(n(\overline{S_3 \cup S_5 \cup S_7})\)を求めてください。
-
\(n(S_3 \cap (\overline{S_5 \cup S_7}))\)を求めてください。
答え
(6)はベン図を使って整理すると分かりやすいです。
-
\(3\)の倍数の最小は\(795 = 3 \cdot 265\),最大は\(1185 = 3 \cdot 395\)です。 また\(5\)の倍数の最小は\(795 = 5 \cdot 159\),最大は\(1185 = 5 \cdot 237\)です。 さらに\(7\)の倍数の最小は\(798 = 7 \cdot 114\),最大は\(1183 = 7 \cdot 169\)です。 したがって,\(S_3\),\(S_5\),\(S_7\)は次の集合です。
\( \begin{align} S_3 &= \{3 \cdot 265,\ 3 \cdot 266,\ \cdots,\ 3 \cdot 395\} \\[5pt] S_5 &= \{5 \cdot 159,\ 5 \cdot 160,\ \cdots,\ 5 \cdot 237\} \\[5pt] S_7 &= \{7 \cdot 114,\ 7 \cdot 115,\ \cdots,\ 7 \cdot 169\} \end{align} \)これより,\(n(S_3)\),\(n(S_5)\),\(n(S_7)\)が求められます。
\( \begin{align} n(S_3) &= 395 - 265 + 1 = \textcolor{red}{131} \\[5pt] n(S_5) &= 237 - 159 + 1 = \textcolor{red}{79} \\[5pt] n(S_7) &= 169 - 114 + 1 = \textcolor{red}{56} \end{align} \) -
\(S_3 \cap S_5\),\(S_5 \cap S_7\),\(S_7 \cap S_3\)は次の集合のことです。 例えば\(3\)の倍数かつ\(5\)の倍数である数とは,\(15\)の倍数のことですよね。
\( \begin{align} S_3 \cap S_5 &= S_{15} \\[5pt] S_5 \cap S_7 &= S_{35} \\[5pt] S_7 \cap S_3 &= S_{21} \end{align} \)\(15\)の倍数の最小は\(795 = 15 \cdot 53\),最大は\(1185 = 15 \cdot 79\)です。 また\(35\)の倍数の最小は\(805 = 35 \cdot 23\),最大は\(1155 = 35 \cdot 33\)です。 さらに\(21\)の倍数の最小は\(798 = 21 \cdot 38\),最大は\(1176 = 21 \cdot 56\)です。 したがって,\(S_{15}\),\(S_{35}\),\(S_{21}\)は次の集合です。
\( \begin{align} S_{15} &= \{15 \cdot 53,\ 15 \cdot 54,\ \cdots,\ 15 \cdot 79\} \\[5pt] S_{35} &= \{35 \cdot 23,\ 35 \cdot 24,\ \cdots,\ 35 \cdot 33\} \\[5pt] S_{21} &= \{21 \cdot 38,\ 21 \cdot 39,\ \cdots,\ 21 \cdot 56\} \end{align} \)これより,\(n(S_3 \cap S_5)\),\(n(S_5 \cap S_7)\),\(n(S_7 \cap S_3)\)が求められます。
\( \begin{align} n(S_3 \cap S_5) &= n(S_{15}) \\[5pt] &= 79 - 53 + 1 = \textcolor{red}{27} \\[5pt] n(S_5 \cap S_7) &= n(S_{35}) \\[5pt] &= 33 - 23 + 1 = \textcolor{red}{11} \\[5pt] n(S_7 \cap S_3) &= n(S_{21}) \\[5pt] &= 56 - 38 + 1 = \textcolor{red}{19} \end{align} \) -
\(S_3 \cap S_5 \cap S_7\)は次の集合のことです。
\( \begin{align} S_3 \cap S_5 \cap S_7 = S_{105} \end{align} \)\(105\)の倍数の最小は\(840 = 105 \cdot 8\),最大は\(1155 = 105 \cdot 11\)です。 したがって,\(S_{105}\)は次の集合です。
\( \begin{align} S_{105} = \{105 \cdot 8,\ 105 \cdot 9,\ \cdots,\ 105 \cdot 11\} \end{align} \)これより,\(n(S_3 \cap S_5 \cap S_7)\)が求められます。
\( \begin{align} n(S_3 \cap S_5 \cap S_7) = 11 - 8 + 1 = \textcolor{red}{4} \end{align} \) -
公式を使って求められます。
\( \begin{align} &n(S_3 \cup S_5 \cup S_7) \\[5pt] &= n(S_3) + n(S_5) + n(S_7) \\[5pt] &\quad - n(S_3 \cup S_5) - n(S_5 \cup S_7) - n(S_7 \cup S_3) \\[5pt] &\quad + n(S_3 \cup S_5 \cup S_7) \\[5pt] &= 131 + 79 + 56 \\[5pt] &\quad - 27 - 11 - 19 \\[5pt] &\quad + 4 \\[5pt] &= \textcolor{red}{213} \end{align} \) -
まず全体集合の要素数を求めておきます。
\( \begin{align} n(U) = 1185 - 794 + 1 = 392 \end{align} \)\(\overline{S_3 \cup S_5 \cup S_7}\)は\(S_3 \cup S_5 \cup S_7\)の補集合ですから,\(n(\overline{S_3 \cup S_5 \cup S_7})\)は次のように求められます。
\( \begin{align} n(\overline{S_3 \cup S_5 \cup S_7}) &= 392 - 213 \\[5pt] &= \textcolor{red}{179} \end{align} \) -
ここまでの情報をベン図に整理してみましょう。 小さい集合から順に要素数を特定できるので,まず次の情報を書き込みます。
\( \begin{align} n(S_3 \cap S_5 \cap S_7) = 4 \end{align} \)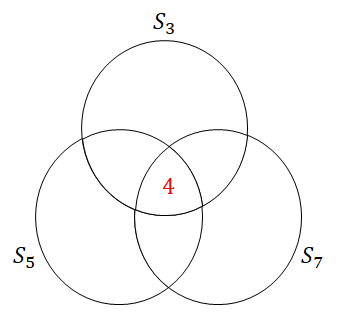
次の情報を使えば,その周りの要素数も特定できます。
\( \begin{align} n(S_3 \cap S_5) &= 27 \\[5pt] n(S_5 \cap S_7) &= 11 \\[5pt] n(S_7 \cap S_3) &= 19 \end{align} \)これらの値には\(n(S_3 \cap S_5 \cap S_7)\)の分が入っていますから,その値を引いてベン図に書き込みます。
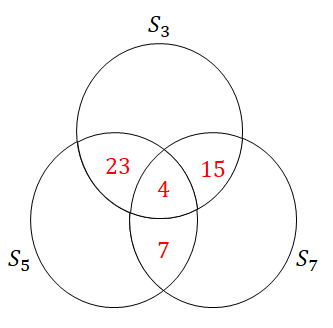
あとは次の情報を使うだけですね。
\( \begin{align} n(S_3) &= 131 \\[5pt] n(S_5) &= 79 \\[5pt] n(S_7) &= 56 \end{align} \)例えば\(n(S_3)\)の値には,\(23\),\(15\),\(4\)の分が入っていますから,その値を引いてベン図に書き込みます。
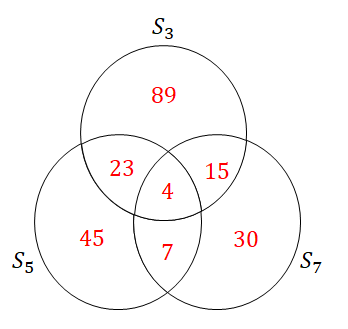
これで要素数の情報を整理できました。 あとは\(n(S_3 \cap (\overline{S_5 \cup S_7}))\)を求めるだけです。 \(S_3 \cap (\overline{S_5 \cup S_7})\)は,ベン図では次の部分ですね。
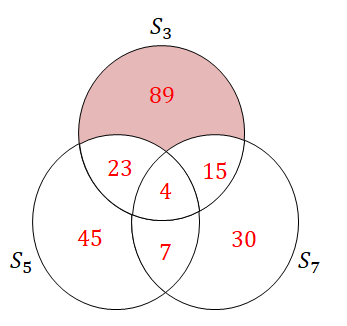
したがって,\(n(S_3 \cap (\overline{S_5 \cup S_7})) = 89\)です。
