目次

• 樹形図
• 辞書式配列
• 和の法則
• 積の法則
• 確認問題

樹形図

場合の数を数えるとき，秩序立った数え方をする必要があります。 例えば本棚にある本を数えるとき，ランダムに目についた本から数えるより，端から順に数えた方がミスをせずに済みますね。

多くの場合の数の問題は，端から数えられるほど単純ではありません。 ですが情報をうまく整理すれば，正しく効率よく場合の数を数えられます。

代表的な情報整理方法は，ありえる場合を樹形図として図示する方法です。 例として，次の集合の部分集合で，要素が\(3\)個であるものの総数を数えます。

樹形図の考え方は，まず\(a\)で始まる集合を徹底的に考え，次に\(b\)で始まる集合を徹底的に考えるというように，"小さいもの"から順序良く全ての場合を数えるものです。 アルファベットの大小は辞書順で考えられます。

ではまず\(a\)で始まる集合を考えてみましょう。 集合の要素をアルファベット順に並べることにすると，\(a\)の次の要素としては\(b\)，\(c\)が考えられます。 これを次のように枝分かれの図にします。

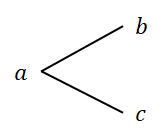
集合の要素が\(3\)つ必要なので，もうひとつ枝分かれが必要です。 \(b\)の次には\(c\)と\(d\)が，\(c\)の次には\(d\)だけが考えられるので，樹形図の続きは次のようになります。

補足 \(a\)の次に\(d\)は来ない

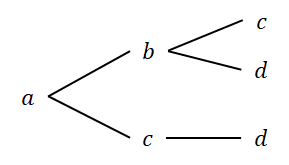
\(a\)の次の要素として\(b\)，\(c\)は考えられますが，\(d\)はあり得ません。 \(d\)より大きい要素がもう無いので，その次の要素がもう考えられないからです。

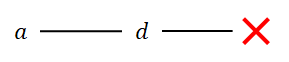
このように，その先が続かない枝は書かないのですが，大きな樹形図になると，その先が続くかどうかの判断が難しいかもしれません。 そんなときは，とりあえず何でも枝分かれを書いてしまって，先が続かない枝は後で消してしまえば良いです。

これで\(a\)で始まる集合は考え尽くしました。 次は\(b\)で始まる集合を考えましょう。 といっても，\(b\)の次は\(c\)，\(d\)と続くしかないですね。 というわけで，次の図が樹形図の完成形です。

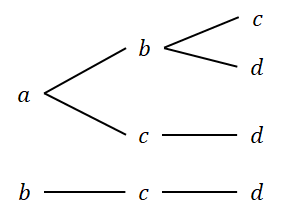
樹形図を見れば，要素が\(3\)個である部分集合の個数が\(4\)であることが分かりますね。 さらに樹形図の枝分かれを左から追えば，\(4\)つの部分集合が以下のものであることも分かります。

辞書式配列

先ほどのような簡単な問題であれば，わざわざ幅をとる樹形図をかかなくても，ありえる場合を辞書順に並べるだけで済みます。

集合の要素を\(abd\)のようにアルファベット順に並べることにして，ありえる部分集合を辞書順に並べることにします。 一番初めに来るものは，左からなるべく小さいアルファベットを並べた次のものですね。

その次は，右の方から少しずつ大きいアルファベットと交換していけば，小さいものから順に考えることができます。 末尾の\(c\)をひとつ大きい\(d\)にしたものが，辞書順で次に来るものです。

次に来るものは何でしょうか？ 末尾はもうより大きいものに交換できませんから，その手前の\(b\)をひとつ大きい\(c\)に交換します。 このとき末尾には\(c\)より大きいものが来ますが，それは\(d\)しかありません。

もう\(c\)も\(d\)もより大きいものに交換できません。 次は頭の\(a\)を\(b\)に交換するしかありませんが，その続きは\(cd\)と続くしかありません。

これで辞書順最大のものが出てきましたから，全部の部分集合が出尽くしたことになります。 この方法でも場合の数は\(4\)ですね。 少しずつ大きいものに取り替える方法に慣れておきましょう。

和の法則

さいころを\(2\)つ振って，出た目の合計が\(11\)以上になる場合の数はいくつでしょうか？ この問題を考えるときは，合計が\(11\)になる場合と\(12\)になる場合に場合分けすると考えやすいです。

まず，出た目の合計が\(11\)になる場合を考えます。 \(2\)つのさいころの目を\((3, 4)\)のように組として表すことにすると，目の合計が\(11\)になるのは，次の\(2\)通りです。

次に出た目の合計が\(12\)になる場合を考えると，次の\(1\)通りしかありませんね。

以上のことから，出た目の合計が\(11\)以上になる場合の数は\(2 + 1 = 3\)です。 場合の数を数えるとき，考えやすいように場合分けすることは大事です。

さて，この項の題になっている和の法則ですが，実はもう使いました。 和の法則の内容は，次の通りです。

和の法則

同時には起こらない\(2\)つの事柄\(A\)，\(B\)の場合の数をそれぞれ\(m\)，\(n\)とする。 このとき，\(A\)または\(B\)が起こる場合の数は，次の通りになる。

\( \begin{align} m + n \end{align} \)

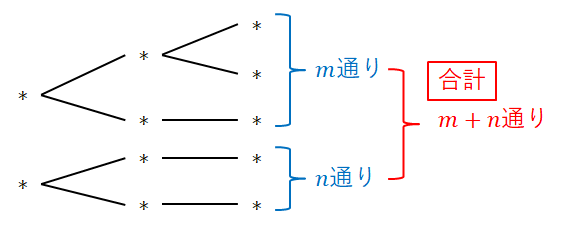
先ほどの場合分けはこの法則を利用しています。 出た目の合計が\(11\)になる場合と\(12\)になる場合は同時には起こりません。 だから\(11\)以上になる場合の数を数えるときは，この２つの場合の数を足せば良かったのです。

もちろん「ある数が偶数になる場合」と「ある数が\(3\)の倍数になる場合」のように同時に起こる可能性がある事柄の場合の数は，そのまま足すわけにはいきません。 足した後に同時に起こる場合の数を引く必要があります。

積の法則

さいころを\(1\)つ振ったとき，出る目の場合の数は\(6\)です。 では，さいころを\(2\)つ振ったとき，出る目の組の場合の数はいくつでしょうか？ \(2\)つのさいころをそれぞれ\(A\)，\(B\)と呼ぶことにします。

まずさいころ\(A\)の目が\(1\)であった場合を考えましょう。 このとき，さいころ\(B\)の目としては\(1\)～\(6\)の\(6\)通りがあります。 さいころ\(A\)の目が\(2\)や\(3\)であった場合も，さいころ\(B\)の目の出方は\(6\)通りあります。

というわけで，さいころ\(2\)つの目の組は次の計算の通り，\(36\)通りあります。

ここでは積の法則を使っています。 次の内容です。

積の法則

事柄\(A\)の場合の数が\(m\)であり，その各場合に対して事柄\(B\)の場合の数が\(n\)であるとする。 このとき，\(A\)と\(B\)がともに起こる場合の数は，次の通りになる。

\( \begin{align} m \times n \end{align} \)

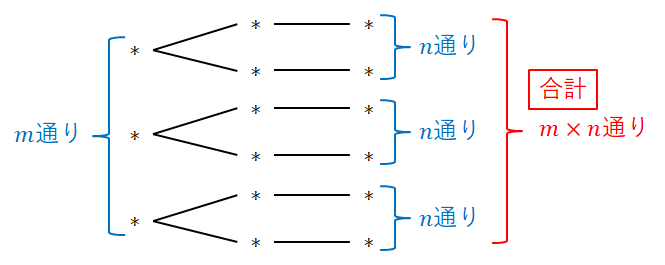
これも和の法則と同じく当たり前の内容です。 \(A\)と\(B\)を組み合わせたときの場合の数というイメージです。 よく見ると積の法則は，和の法則を繰り返し使った結果ですね。 特に新しい事実でもありません。

確認問題

次の\(5\)つのアルファベットから\(3\)つを選び，\(1\)列に並べてできる\(3\)文字の文字列はいくつあるか答えてください。

\( \begin{align} a,\ a,\ b,\ b,\ c \end{align} \)

答え

樹形図を使う方法，辞書順で考える方法の両方を試してみます。

[1] まずは樹形図で考えます。 各アルファベットがいくつあるかに注意すると，樹形図が次のようになることが分かります。

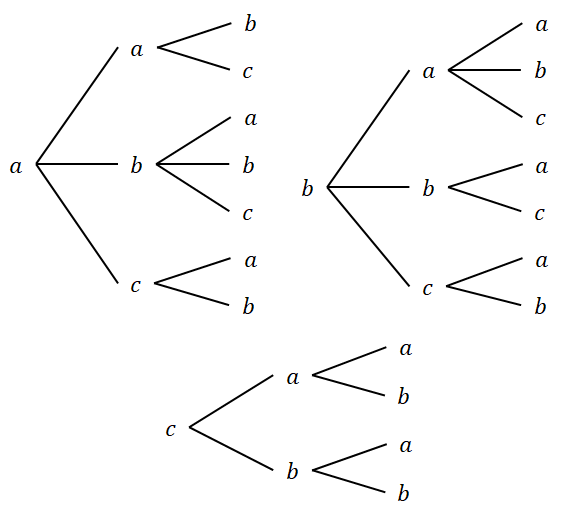
樹形図より，できる文字列は\(18\)個あることが分かります。

---

[2] 辞書順でも考えてみます。 まず辞書順で一番小さい文字列は，左からなるべく小さいアルファベットを並べた次の文字列です。

\( \begin{align} aab \end{align} \)

次の文字列は，末尾をひとつ大きいアルファベットに交換したものです。

\( \begin{align} aac \end{align} \)

次は末尾をより大きいアルファベットに変えられませんから，２文字目の\(a\)をひとつ大きい\(b\)に交換することになります。 そして，末尾のアルファベットは改めてなるべく小さいものに交換します。

\( \begin{align} aba \end{align} \)

この手順を繰り返していくと，次のようにできる文字列が辞書順で分かります。

\( \begin{align} &aab,\ aac,\ aba,\ abb,\ abc \\[5pt] &aca,\ acb,\ baa,\ bab,\ bac \\[5pt] &bba,\ bbc,\ bca,\ bcb,\ caa \\[5pt] &cab,\ cba,\ cbb \end{align} \)

したがって，できる文字列は\(18\)個あります。