目次

• 合同・相似の証明
• 平行の証明
• 特定の図形である証明
• 円に関する証明
• 共点の証明
• 共線の証明
• 確認問題

合同・相似の証明

三角形の合同や相似を示す方法を確認します。 前回確認したばかりなので，合同条件や相似条件だけさらっと見ておきましょう。

まずは合同条件です。 合同条件は，三角形の形・大きさを確定する情報が等しいことを確認する条件でした。

次は相似条件です。 相似条件は，図形の形が同じであれば良いので，合同よりも条件がゆるくなっています。

平行の証明

\(2\)本の直線（線分）が平行であることの示し方を確認しましょう。 それは，この\(2\)本の直線を横切る直線（線分）を手掛かりに考えます。

平行と同位角・錯角

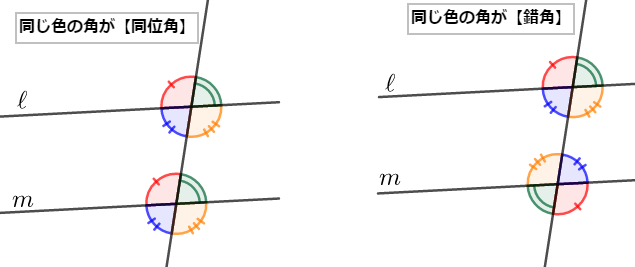
\(1\)つの直線が\(2\)本の直線\(\ell\)，\(\mathcal{m}\)と交わるとき，次のいずれかが成り立てば，\(\ell\)と\(\mathcal{m}\)は平行である。

1. 同位角が等しい。
2. 錯角が等しい。

また，線分の比による証明方法もあります。 前回学んだものです。

線分の比による証明

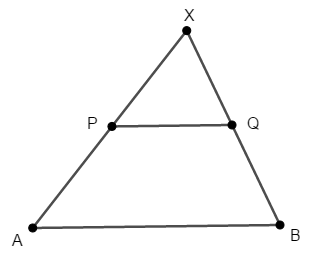
\(\triangle\mathrm{XAB}\)の辺\(\mathrm{XA}\)上に点\(\mathrm{P}\)，辺\(\mathrm{XB}\)上に点\(\mathrm{Q}\)があるとき，次のいずれかが成り立てば\(\mathrm{AB} /\!/ \mathrm{PQ}\)である。

1. \(\mathrm{XP} : \mathrm{XA} = \mathrm{XQ} : \mathrm{XB}\)
2. \(\mathrm{XP} : \mathrm{PA} = \mathrm{XQ} : \mathrm{QB}\)

---

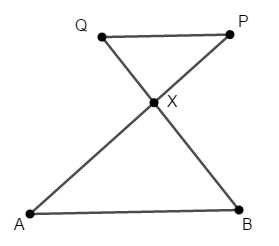
\(\triangle\mathrm{XAB}\)の辺\(\mathrm{XA}\)の延長上の\(\mathrm{X}\)側に点\(\mathrm{P}\)，辺\(\mathrm{XB}\)の延長上の\(\mathrm{X}\)側に点\(\mathrm{Q}\)があるとき，次のいずれかが成り立てば\(\mathrm{AB} /\!/ \mathrm{PQ}\)である。

1. \(\mathrm{XP} : \mathrm{XA} = \mathrm{XQ} : \mathrm{XB}\)
2. \(\mathrm{XP} : \mathrm{PA} = \mathrm{XQ} : \mathrm{QB}\)

これも結局は同位角・錯角が等しいことから導かれるものです。 同位角・錯角が等しいことは，三角形の相似から導かれます。

とにかく\(2\)直線が平行であることを示すには，同位角・錯角が等しいことを示せば良いと覚えておけばＯＫです。

特定の図形である証明

ある図形が特定の性質をもつ図形であることの証明を確認します。 例えば，三角形が二等辺三角形であることの証明などです。

このような証明には，定義を満たすことを直接証明するのが基本ですが，他の条件により示せることもあります。 どんな条件があるのか，しっかり確認しておきましょう。

まずは簡単な図形として，正三角形であることの証明を確認します。

正三角形の証明

次のいずれかの条件を満たす三角形は，正三角形である。

1. 【定義】\(3\)辺の長さが等しい。
2. 内角が全て等しい。

次は二等辺三角形です。

二等辺三角形の証明

次のいずれかの条件を満たす三角形は，二等辺三角形である。

1. 【定義】\(2\)辺の長さが等しい。
2. \(2\)つの内角が等しい。

直角三角形も確認しましょう。

直角三角形の証明

次のいずれかの条件を満たす三角形は，直角三角形である。 三角形の\(3\)辺の長さを\(a\)，\(b\)，\(c\)（\(c\)が最長）とする。

1. 【定義】\(1\)つの内角が直角である。
2. \(a^2 + b^2 = c^2\)を満たす。

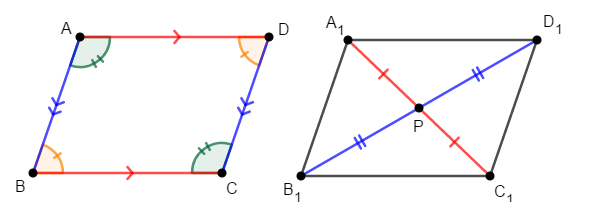
次は四角形の証明を確認していきます。 まずは平行四辺形です。

平行四辺形の証明

次のいずれかの条件を満たす四角形は，平行四辺形である。

1. 【定義】\(2\)組の対辺がそれぞれ平行である。
2. \(2\)組の対辺がそれぞれ等しい。
3. \(2\)組の対角がそれぞれ等しい。
4. \(1\)組の対辺が平行であり，長さが等しい。
5. \(2\)本の対角線がそれぞれの中点で交わる。

次は長方形です。

長方形の証明

次のいずれかの条件を満たす四角形は，長方形である。

1. 【定義】内角が全て等しい。
2. 平行四辺形であり，対角線の長さが等しい。

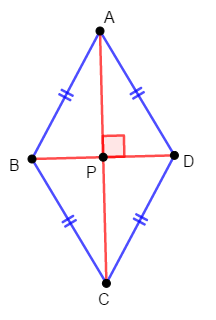
次はひし形です。

ひし形の証明

次のいずれかの条件を満たす四角形は，ひし形である。

1. 【定義】辺の長さがすべて等しい。
2. 平行四辺形であり，対角線が垂直に交わる。

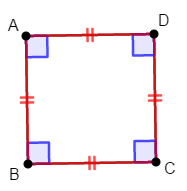
最後に正方形です。

正方形の証明

長方形であり，ひし形でもある四角形は，正方形である。 つまり，内角がすべて等しく，辺の長さがすべて等しい四角形は，正方形である。

各図形の定義は覚えておきましょう。 他の条件はその図形が持つ性質をよく理解しておけば，思い出せるはずです。

円に関する証明

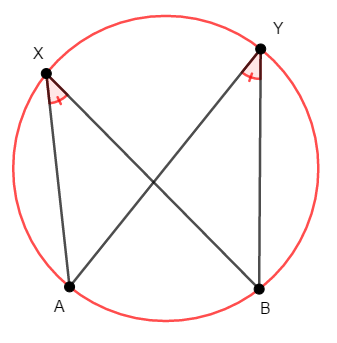
円に関する証明を確認していきましょう。 まずはある\(4\)点が同一円周上にあることの証明を確認します。 この証明には円周角の定理の逆を利用できます。

円周角の定理の逆

\(2\)点\(\mathrm{X}\)，\(\mathrm{Y}\)が直線\(\mathrm{AB}\)に対して同じ側にあり，次が成り立つとき，\(4\)点\(\mathrm{A}\)，\(\mathrm{B}\)，\(\mathrm{X}\)，\(\mathrm{Y}\)は同一円周上にある。

\( \begin{align} \angle \mathrm{AXB} = \angle \mathrm{AYB} \end{align} \)

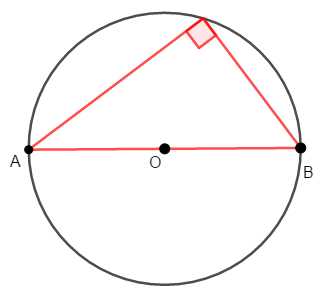
ある弦が直径であることの証明方法も確認しておきましょう。

タレスの定理の逆

ある弦に対する円周角が直角であるとき，その弦は直径である。

もうひとつ，円周上の点を通る直線が接線であることの証明も確認します。

接線の証明

円周上の点を通る直線が，その点を通る半径に垂直であるとき，この直線はこの円の接線である。

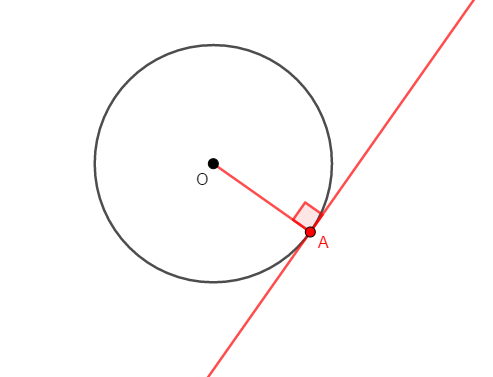
どれも重要な定理の逆です。 普段から定理の逆も成り立つかを確認しておくと役に立ちます。

共点の証明

いくつかの直線が\(1\)点で交わるとき，これらの直線は共点であるといいます。 \(3\)本の直線について，こうなるための条件，すなわち共点条件を考えてみましょう。

数学Ｂのベクトルなどを使えば考えやすいのですが，数学Ａの平面図形の問題としては，とりあえず以下のいずれかの方針で取り組むことになります。

• \(2\)直線の交点をもう\(1\)つの直線が通ることを示す。
• \(2\)直線ずつの交点が一致することを示す。
• チェバの定理の逆を利用する。（今回は扱いませんが，また後に解説します。）

基本的には，\(3\)つのものを同時には考えられないので，\(2\)つずつのペアで考えるという発想です。 \(1\)つめの方針は「直線・直線ペア → 交点・直線ペア」，\(2\)つめの方針は「直線・直線ペア → 交点・交点ペア」で考えるわけです。

まず\(1\)つめの方針「\(2\)直線の交点をもう\(1\)つの直線が通ることを示す」を考えてみましょう。

この方針では，直線上の点が持つ性質を理解することが重要です。 \(2\)直線の交点は，それらの直線の性質を併せ持ちます。 この交点が残り\(1\)直線の上に乗るための性質を持つことを示せば良いのです。

イメージしづらいと思うので，補足で具体例を見てみましょう。

次に\(2\)つめの方針「\(2\)直線ずつの交点が一致することを示す」を考えてみましょう。

この方針では，\(2\)点が一致することを示す必要があります。 そのひとつの方法は，まず\(2\)点が同じ線分上にあることを確認し，両点がその線分を同じ比で内分（外分）することを示すことです。

内分・外分については，次回学びます。

共線の証明

いくつかの点が一直線上にあるとき，これらの点は共線であるといいます。 \(3\)つの点について，こうなるための条件，すなわち共線条件を考えてみましょう。

これも数学Ｂのベクトルなどを使うと考えやすいのですが，数学Ａの平面図形の問題としては，とりあえず以下のいずれかの方針で取り組みます。

• \(2\)点を結ぶ直線上にもう\(1\)つの点があることを示す。
• \(2\)点ずつを結んでできる\(2\)直線が平行であることを示す。
• \(3\)点のなす角が\(180^{\circ}\)であることを示す。（\(3\)点の順番に注意）
• メネラウスの定理の定理の逆を利用する。（今回は扱いませんが，また後に解説します。）

初めの\(2\)つは共点条件と同じく，同時に\(3\)つは考えられないので，\(2\)つずつのペアで考えるものです。 \(3\)つめは共線条件ならではですね。

まず\(1\)つめの方針「\(2\)点を結ぶ直線上にもう\(1\)つの点があることを示す」を考えてみましょう。

理屈としては理解できる方針ですね。 共点の「\(2\)直線の交点をもう\(1\)つの直線が通ることを示す」方針と似ています。

この共線条件も共点の場合と同じく，\(2\)点を結ぶ直線の持つ性質や，残りの\(1\)点の性質を把握することが重要です。 イメージしづらければ，共点条件の方の補足を見てみてください。

（ただ平面図形の問題としては，この方針はあまり使わない気がします。）

次に\(2\)つめの方針「\(2\)点ずつを結んでできる\(2\)直線が平行であることを示す」を考えてみましょう。

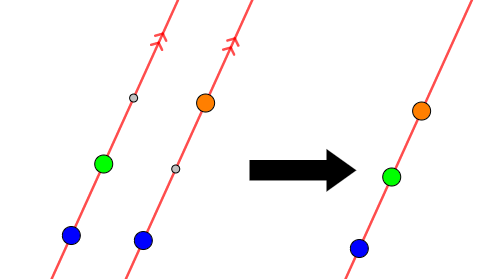
このとき\(2\)つの直線は，必ず\(1\)点を共有することになります。 \(3\)点しかないので，完全に別々の点を\(2\)個ずつ選ぶことはできないのです。 \(1\)点を共有した直線が平行なら，それらは同じ直線なので，結局\(3\)点が同一直線上にあることになります。

\(2\)つの直線が平行であることを示すには，同位角か錯角が等しいことを示せば良いですね。

もし\(2\)つの直線が平行であることを直接示せない場合は，これら両方の直線が，それとは別のある直線\(\ell\)と平行であることを示します。 これで\(2\)つの直線が平行であることを間接的に示せます。

最後に\(3\)つめの方針「\(3\)点のなす角が\(180^{\circ}\)であることを示す」を考えてみましょう。

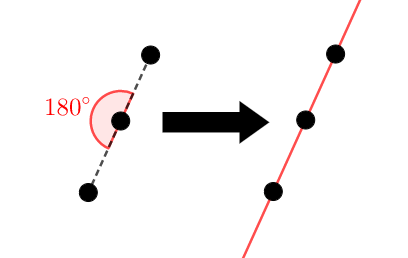
これは使いやすい証明方法です。 \(3\)点のなす角が\(180^{\circ}\)であることを示すには，次のように角をいくつかに分割して，その合計が\(180^{\circ}\)になることを確認すれば良いです。

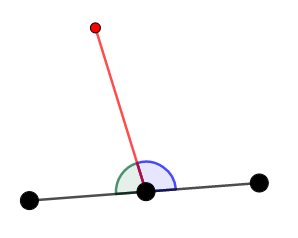
角のとり方を間違えると，\(3\)点のなす角が\(0^{\circ}\)となり，考えづらくなります。 \(3\)点がどんな順番で並びそうか，見当をつけてから角度を考えていくと良いですね。

次回からは高校数学の平面図形に入っていきます。 今回復習したことの応用例は，今後たくさん出てきますから，今回の確認問題は軽めにしておきます。

確認問題

次図のように長方形\(\mathrm{ABCD}\)の各辺上に中点\(\mathrm{P}\)，\(\mathrm{Q}\)，\(\mathrm{R}\)，\(\mathrm{S}\)をとります。 このとき，\(\mathrm{PQ} /\!/ \mathrm{RS}\)であることを証明してください。

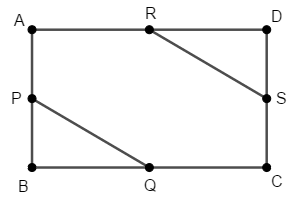
答え

\(2\)直線が平行であることを証明するには，同位角か錯角が等しくなることを示せばよいです。

そのために\(\mathrm{PQ}\)，\(\mathrm{RS}\)と交わる直線を引く必要があるので，次のように線分\(\mathrm{PS}\)を引きます。 錯角である\(\angle\mathrm{QPS}\)と\(\angle\mathrm{RSP}\)が等しいことを証明します。

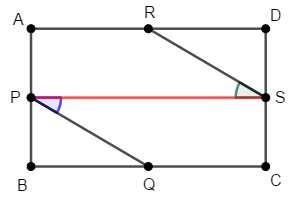
四角形\(\mathrm{ABCD}\)は長方形ですから，\(\angle\mathrm{B}\)も\(\angle\mathrm{D}\)も直角です。 また対辺が等しく，点\(\mathrm{P}\)，\(\mathrm{Q}\)，\(\mathrm{R}\)，\(\mathrm{S}\)は各辺の中点なので，次が成り立ちます。

\( \begin{align} \mathrm{BP} &= \mathrm{DS} \\[5pt] \mathrm{BQ} &= \mathrm{DR} \end{align} \)

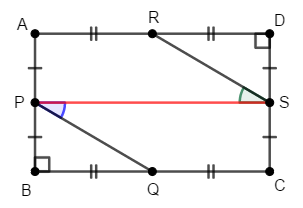
したがって，\(2\)辺とその間の角がそれぞれ等しいので，\(\triangle\mathrm{BPQ}\)と\(\triangle\mathrm{DSR}\)は合同です。 よって，\(\angle\mathrm{BPQ} = \angle\mathrm{DSR}\)です。

また四角形\(\mathrm{ABCD}\)は長方形ですから，\(\mathrm{AB} /\!/ \mathrm{DC}\)であり，その錯角は等しいです。 したがって，次が成り立ちます。

\( \begin{align} \angle\mathrm{BPS} &= \angle\mathrm{DSP} \\[5pt] \angle\mathrm{BPQ} + \angle\mathrm{QPS} &= \angle\mathrm{DSR} + \angle\mathrm{RSP} \\[5pt] \angle\mathrm{QPS} &= \angle\mathrm{RSP} \end{align} \)

途中で\(\angle\mathrm{BPQ} = \angle\mathrm{DSR}\)であることを使いました。 したがって，錯角が等しいので，\(\mathrm{PQ} /\!/ \mathrm{RS}\)です。

---

このような簡単な図形が問題になると，見るからに直角の角や，見るからに平行な直線が出てきますが，見た目だけで判断してはいけません。 定理として学んでいないことは，まず証明しましょう。

中線定理という定理を証明してください。 中線定理は，以下の内容です。

【中線定理】\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\)の中点を\(\mathrm{M}\)とする。 このとき，次が成り立つ。

\( \begin{align} \mathrm{AB}^2 + \mathrm{AC}^2 = 2(\mathrm{AM}^2 + \mathrm{BM}^2) \end{align} \)

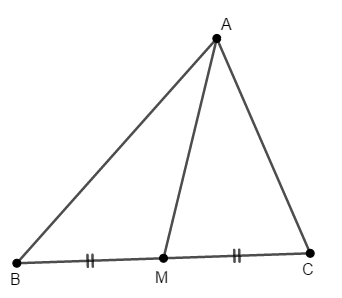
中線定理を証明してください。 ただし\(\triangle\mathrm{ABC}\)が鋭角三角形（すべての角が鋭角）の場合だけで良いです。 鈍角三角形の場合も同様に証明できます。

---

この定理を覚えておくと，役に立つ場面があります。 ただし覚えていなくても，この証明ができるくらいの思考力があれば，特別困る場面はありません。

答え

三角形に関する式で，\(2\)乗の形があるので，三平方の定理を利用することを考えます。 そのために頂点\(\mathrm{A}\)から対辺に垂線\(\mathrm{AH}\)を下ろします。

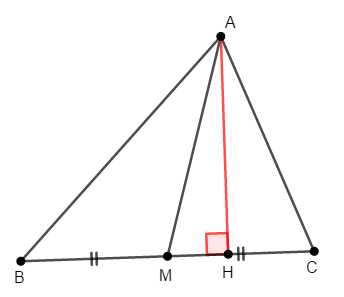
\(\mathrm{AB} < \mathrm{AC}\)の場合は点\(\mathrm{H}\)は線分\(\mathrm{BM}\)上にありますが，全く同様の議論なので，\(\mathrm{AB} \geqq \mathrm{AC}\)の場合のみ証明します。 この場合，点\(\mathrm{H}\)は線分\(\mathrm{CM}\)上にあり，特に\(\mathrm{AB} = \mathrm{AC}\)の場合は，\(\mathrm{M}\)と\(\mathrm{H}\)は一致します。

では証明したい式の左辺から計算を始めて，右辺の形になることを確認しましょう。 \(\triangle\mathrm{ABH}\)，\(\triangle\mathrm{ACH}\)は直角三角形ですから，三平方の定理により次のように計算できます。

\( \begin{align} &\quad \mathrm{AB}^2 + \mathrm{AC}^2 \\[5pt] &= \mathrm{AH}^2 + \mathrm{BH}^2 + \mathrm{AH}^2 + \mathrm{CH}^2 \\[5pt] &= 2\mathrm{AH}^2 + \mathrm{BH}^2 + \mathrm{CH}^2 \end{align} \)

この式には\(\mathrm{M}\)が登場せず，\(\mathrm{H}\)が現われています。 \(\mathrm{AH}^2\)，\(\mathrm{BH}^2\)，\(\mathrm{CH}^2\)を次のように\(\mathrm{M}\)を使う形に書き直してみましょう。

\(\triangle\mathrm{AMH}\)が直角三角形であることに注意してください。

\( \begin{align} \mathrm{AH}^2 &= \mathrm{AM}^2 - \mathrm{MH}^2 \\[5pt] \mathrm{BH}^2 &= (\mathrm{BM} + \mathrm{MH})^2 \\[5pt] &= \mathrm{BM}^2 + 2 \mathrm{BM} \cdot \mathrm{MH} + \mathrm{MH}^2 \\[5pt] \mathrm{CH}^2 &= (\mathrm{CM} - \mathrm{MH})^2 \\[5pt] &= (\mathrm{BM} - \mathrm{MH})^2 \\[5pt] &= \mathrm{BM}^2 - 2 \mathrm{BM} \cdot \mathrm{MH} + \mathrm{MH}^2 \end{align} \)

式の途中で\(\mathrm{BM} = \mathrm{CM}\)であることを使いました。 これで先ほどの式の続きを計算できます。

\( \begin{align} \mathrm{AB}^2 + \mathrm{AC}^2 &= 2\mathrm{AH}^2 + \mathrm{BH}^2 + \mathrm{CH}^2 \\[5pt] &= 2\mathrm{AM}^2 - 2\mathrm{MH}^2 \\[5pt] &\phantom{=} + \mathrm{BM}^2 + 2 \mathrm{BM} \cdot \mathrm{MH} + \mathrm{MH}^2 \\[5pt] &\phantom{=} + \mathrm{BM}^2 - 2 \mathrm{BM} \cdot \mathrm{MH} + \mathrm{MH}^2 \\[5pt] &= 2\mathrm{AM}^2 + 2\mathrm{BM}^2 \\[5pt] &= 2(\mathrm{AM}^2 + \mathrm{BM}^2) \end{align} \)

これで中線定理が証明できました。