今回も中学校の平面図形の復習です。 三角形の合同・相似について,しっかり理解しておきましょう。
目次
三角形の合同
\(2\)つの図形が全く同じ形・大きさをしているとき,これらの図形は合同であるといいます。 次の三角形はすべて合同です。
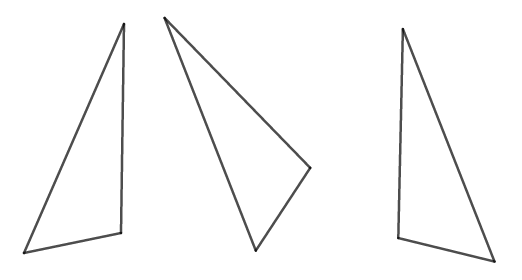
真ん中の三角形は左の三角形を回転したもの,右の三角形は左の三角形を裏返したものです。 これらはすべて同じ形・大きさですね。
言い方を変えれば,\(2\)つの図形が合同であるとは,一方の図形を移動させることで,もう一方の図形に重ね合わせられるということです。 この移動には次の\(3\)種類があります。
- 平行移動(図形をそのままスライドさせる移動)
- 回転移動(図形を回転させる移動)
- 対称移動(図形を裏返す移動)
それでは三角形の合同条件を思い出しましょう。
\(2\)つの三角形は,次のいずれかが成り立つとき,合同である。
- \(3\)辺がそれぞれ等しい。
- \(2\)辺とその間の角がそれぞれ等しい。
- \(1\)辺とその両端の角がそれぞれ等しい。
覚えるのが大変だ! という意見もあると思いますが,そもそもなぜこれが合同条件になるのかを考えれば,忘れることはありません。
三角形の形・大きさを決めるには,\(3\)つの情報が必要です。 例えば\(3\)辺の長さが分かれば,それがどんな三角形かは完全に決まります。 合同条件は,このような「三角形を完全に決める条件」からできていることを念頭に置いてください。
それでは順に合同条件を見ていきます。 まず\(1\)つめの合同条件です。
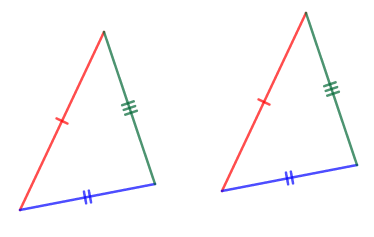
この合同条件は,三角形を完全に決める条件として「\(3\)辺の長さ」を使っています。 \(3\)辺の長ささえ決まれば,それがどんな三角形かは完全に決まります。
次に\(2\)つめの合同条件です。
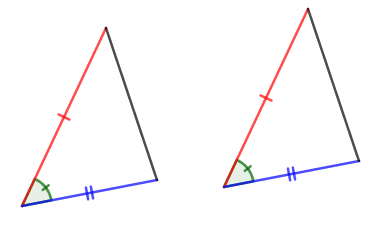
この合同条件も,三角形を完全に決めるための\(3\)つの情報からできています。 \(2\)辺の長さが分かって,その間の開き具合が分かれば,それがどんな三角形かは完全に決まります。
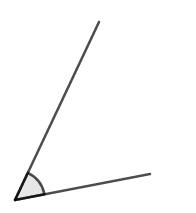
次に\(3\)つめの合同条件です。
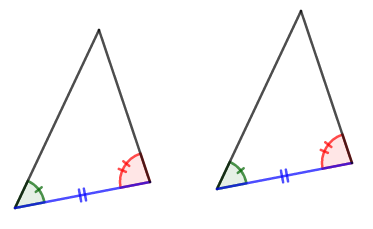
この合同条件も,三角形を完全に決めるための\(3\)つの情報からできています。 \(1\)辺の長さが分かって,それが他の\(2\)辺となす角が分かれば,それがどんな三角形かは完全に決まります。
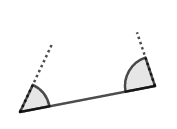
合同条件は,このような三角形を決める情報が完全に一致するから,それらの三角形は合同だという意味なのです。
三角形が完全に決まるには\(3\)つの情報が必要ですが,\(3\)つあれば何でも良いわけではありません。 例えば\(3\)つの角が分かっただけでは,それがどんな三角形かはまだ分かりません。 これでは三角形の形は決まるものの,その大きさが決まらないからです。
これは,「三角形の内角の和は\(180^{\circ}\)」という事実があるからです。 この事実を使えば,\(2\)つの角が分かった時点で,もう\(1\)つの角も分かります。
なので角の情報が\(3\)つ分かっても,その内\(1\)つは「言われなくても分かってる」情報であり,意味がないのです。 \(3\)つの角の情報は,実質\(2\)つ分の情報しかなく,三角形が完全には決まらないわけです。
直角三角形のような特別な三角形の合同条件も考えてみましょう。 もちろんこれも三角形なので,上で見た合同条件が使えますが,直角三角形ならではの合同条件も考えられます。
合同条件が「三角形を決める\(3\)つの情報」からなることを思い出しましょう。 直角三角形は「\(1\)つの角が直角である」という情報をあらかじめ持っていますから,三角形を決める情報を残り\(2\)つ考えれば,合同条件にできます。 具体的には,次のような合同条件を考えられます。
\(2\)つの直角三角形は,次のいずれかが成り立つとき,合同である。
- 斜辺と他の\(1\)辺がそれぞれ等しい。
- 斜辺と\(1\)つの鋭角がそれぞれ等しい。
\(1\)つめの合同条件について確認します。
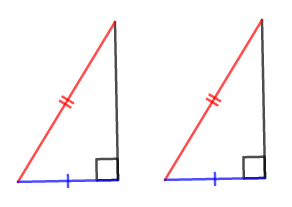
図を見ると,一見合同条件が揃っていないように見えるかもしれません。 そこで三平方の定理を思い出しましょう。 なんと残りの\(1\)辺の長さも分かってしまいます。
これで\(3\)辺がそれぞれ等しいことになるので,合同条件を満たしていることが分かります。
上の合同条件は,「斜辺以外の\(2\)辺がそれぞれ等しい」でもOKです。 この条件が成り立てば,斜辺も等しいことになり,三角形の合同条件「\(3\)辺がそれぞれ等しい」を満たすからです。
しかし,普通は「斜辺と他の\(1\)辺がそれぞれ等しい」の方を習います。 これは他の辺と比べて,斜辺の方がその直角三角形の特徴をよく捉えているからです。
なので学校で習うどちらの合同条件にも「斜辺が等しい」が共通しています。
次に\(2\)つめの合同条件について確認します。
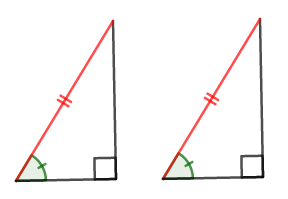
このとき,直角三角形の角度が\(2\)つ分かっていますから,残り\(1\)つも分かります。 三角形の内角の和はいつも\(180^{\circ}\)だからですね。
これで\(1\)辺(斜辺)とその両端の角がそれぞれ等しいことになるので,合同条件を満たしていることが分かります。
直角三角形の合同条件は,とにかく斜辺が等しいことは必要で,それに加えてもう\(1\)つ辺か角(直角以外)が等しければ良いわけですね。
直角三角形には「必ず直角がある」という情報が初めからあります。 だからあと\(2\)つの情報だけで合同条件が成り立ちました。
同様に二等辺三角形にも「\(2\)辺が等しい」という情報がありますから,あと\(2\)つの情報だけで合同条件になります。
学校で習うものでもないし,覚える必要もありませんが,考えてみると良い練習になります。 確認問題で挑戦してみてください。
三角形の相似
\(2\)つの図形が全く同じ形をしているとき,これらの図形は相似であるといいます。 大きさは違っても構いませんから,大きさの比である相似比も重要な情報です。 (大きさまで同じだと合同というのでした。)
次の三角形はすべて相似です。
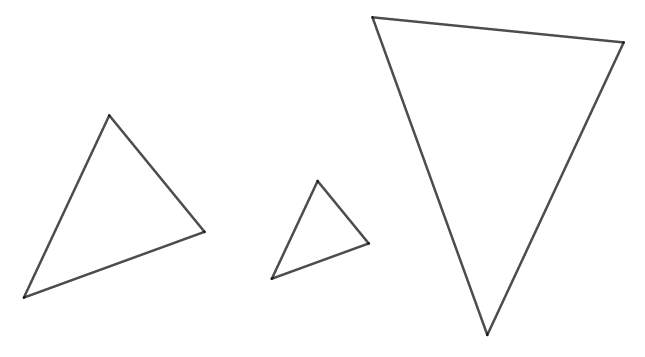
真ん中の三角形は左の三角形を縮小したもの,右の三角形は左の三角形を拡大・回転したものです。 これらはすべて同じ形ですね。
それでは三角形の相似条件を思い出しましょう。
\(2\)つの三角形は,次のいずれかが成り立つとき,相似である。
- \(3\)組の辺の比が等しい。
- \(2\)組の辺の比が等しく,その間の角が等しい。
- \(2\)組の角がそれぞれ等しい。
これも覚えるのが大変だ! と思うかもしれませんが,合同条件を少しゆるめたものと考えれば,いくらか分かりやすいと思います。
それでは順に相似条件を見ていきます。 まず\(1\)つめの相似条件です。
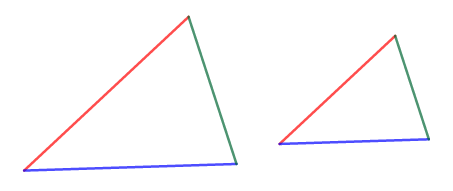
これは合同条件でいうところの「\(3\)辺がそれぞれ等しい」です。 これを少しゆるめて,「辺の長さが一致しなくても比が合ってればOK!」にしたのが相似条件です。
次に\(2\)つめの相似条件です。
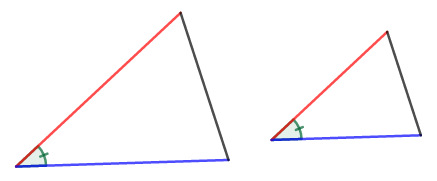
これは合同条件でいうところの「\(2\)辺とその間の角がそれぞれ等しい」です。 これを少しゆるめて,「辺の長さが一致しなくても比が合ってればOK!」にしたのが相似条件です。
次に\(3\)つめの相似条件です。
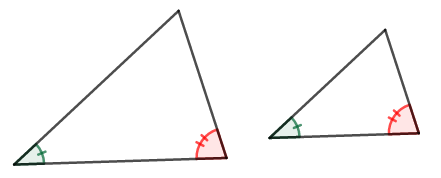
これは合同条件でいうところの「\(1\)辺とその両端の角がそれぞれ等しい」です。 何だか全然違う条件に見えますね。 実はこの相似条件は,合同条件の「両端の角がそれぞれ等しい」の部分だけが残ったものです。
三角形の内角の和は\(180^{\circ}\)と決まっていますから,\(2\)つの角が等しければ,結局全ての角が等しいことになります。 全ての角が等しければその時点で相似ですから,もはや辺の情報は必要なくなるのです。
平行線と線分の比
三角形の相似の重要な応用を考えましょう。 次のように平行な線分\(\mathrm{AB}\),\(\mathrm{PQ}\)を考えます。
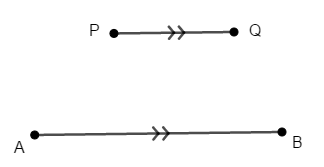
これを横切る\(2\)本の線分を考え,その交点を\(\mathrm{X}\)とします。
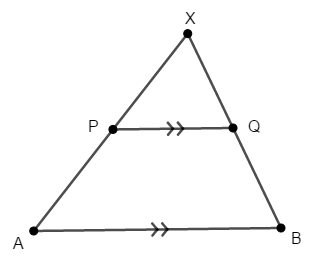
平行線とそれを横切る線分といえば,同位角・錯角です。 等しい同位角を色分けして表すと,次のようになります。
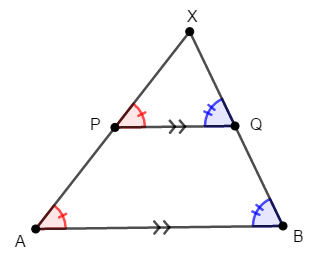
ここで\(\triangle\mathrm{XAB}\)と\(\triangle\mathrm{XPQ}\)に注目すると,\(2\)組の角が等しいので相似です。 したがって対応する辺の比が等しいので,次が成り立ちます。
上の議論で「\(\triangle\mathrm{XAB}\)と\(\triangle\mathrm{PQX}\)は相似である」といってはいけません。 必ず対応する角を同じ順番で並べる必要があります。
上の\(\triangle\mathrm{XAB}\)と\(\triangle\mathrm{XPQ}\)の場合は,「色なしの角 → 赤い角 → 青い角」の順で対応を表しています。 他にも「\(\triangle\mathrm{ABX}\)と\(\triangle\mathrm{PQX}\)は相似である」のように表しても構いません。 対応する角が同じ順番で並べば良いのです。
合同の表し方にも同じルールがありますから,注意してください。
ここで次のように線分\(\mathrm{PA}\)と平行な線分\(\mathrm{QY}\)を引きます。
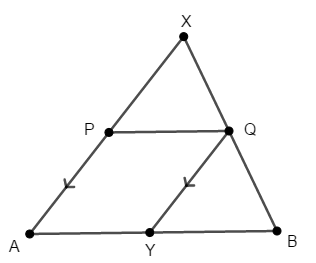
すると図が平行線だらけになり,等しい同位角がたくさん現れます。 等しい同位角を色分けして表すと,次のようになります。
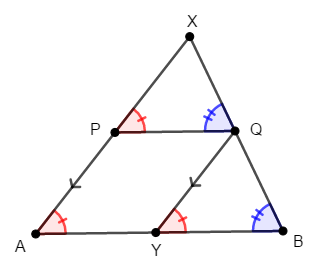
ここで\(\triangle\mathrm{XPQ}\)と\(\triangle\mathrm{QYB}\)は\(2\)組の角が等しいので相似であり,次が成り立ちます。
さらに四角形\(\mathrm{APQY}\)が平行四辺形であることから,\(\mathrm{QY} = \mathrm{PA}\)ですから,次が成り立ちます。
上図でいきなり線分\(\mathrm{QY}\)を引いたので,「何で!?」となったかもしれません。 これは結論から迎えに行ったからです。 初めから上の比の式を証明したかったので,\(\mathrm{PA}\)と等しい線分を\(\mathrm{QY}\)として作り,三角形の相似を利用したのでした。
以上をまとめると,平行線と線分の比について,次が成り立ちます。
\(\triangle\mathrm{XAB}\)の辺\(\mathrm{XA}\)上に点\(\mathrm{P}\),辺\(\mathrm{XB}\)上に点\(\mathrm{Q}\)があり,\(\mathrm{AB} /\!/ \mathrm{PQ}\)であるとき,次が成り立つ。
- \(\mathrm{XP} : \mathrm{XA} = \mathrm{XQ} : \mathrm{XB}\)
- \(\mathrm{XP} : \mathrm{XA} = \mathrm{PQ} : \mathrm{AB}\)
- \(\mathrm{XP} : \mathrm{PA} = \mathrm{XQ} : \mathrm{QB}\)

これは三角形の相似を考えればすぐ分かることなので,わざわざ暗記しなくても困りません。 また,次のように逆が成り立つ場合があり,これも重要です。
\(\triangle\mathrm{XAB}\)の辺\(\mathrm{XA}\)上に点\(\mathrm{P}\),辺\(\mathrm{XB}\)上に点\(\mathrm{Q}\)があるとき,次のいずれかが成り立てば\(\mathrm{AB} /\!/ \mathrm{PQ}\)である。
- \(\mathrm{XP} : \mathrm{XA} = \mathrm{XQ} : \mathrm{XB}\)
- \(\mathrm{XP} : \mathrm{PA} = \mathrm{XQ} : \mathrm{QB}\)
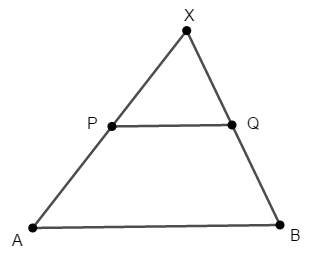
ここでは逆の証明は省略しますが,自力で考えてみてください。 平行であることを示すには,同位角が等しいことを示せばよく,そのために三角形の相似を利用すると良いです。
上の図で点\(\mathrm{X}\)が平行線\(\mathrm{AB}\)と\(\mathrm{PQ}\)の間にあるときは,次の図の様になります。 (\(\mathrm{P}\),\(\mathrm{Q}\)の順番に注意してください。)
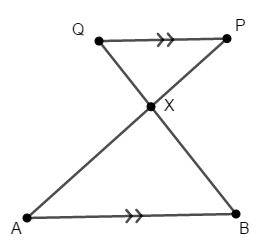
この図に関しても,先ほど学んだ式がそのままの記号で成り立ちます。 先ほどは同位角に注目して相似関係が得られましたが,この場合は錯角に注目すれば良いですね。
逆も同じように成り立ちます。 線分\(\mathrm{AB}\),\(\mathrm{PQ}\)が平行かどうか分かっていない下図のような状況を考えます。
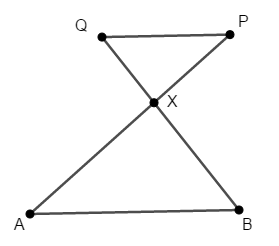
このとき,次のいずれかが成り立てば,\(\mathrm{AB} /\!/ \mathrm{PQ}\)であることが分かります。
- \(\mathrm{XP} : \mathrm{XA} = \mathrm{XQ} : \mathrm{XB}\)
- \(\mathrm{XP} : \mathrm{PA} = \mathrm{XQ} : \mathrm{QB}\)
この項で学んだことは,三角形の相似を考えればすぐ分かることであり,わざわざ暗記する必要はありません。 次のことを掴めれば十分でしょう。
- 平行線があると同位角・錯角同士が等しくなるので,登場する三角形が相似になりがち。
- 相似な三角形が見つかれば,同位角・錯角同士が等しくなる場合があり,このとき平行線が見つかる。
中点連結定理
平行線と線分の比の中でも,次の場合は特別に中点連結定理と呼ばれ,よく使われます。
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{AB}\),\(\mathrm{AC}\)の中点をそれぞれ\(\mathrm{M}\),\(\mathrm{N}\)とすると,次が成り立つ。
- \(\mathrm{BC} /\!/ \mathrm{MN}\)
- \(\mathrm{BC} = 2 \mathrm{MN}\)
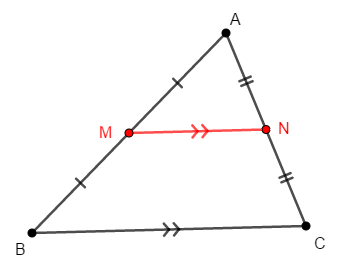
これは簡単に証明できますから,練習としてやってみましょう。 \(\triangle\mathrm{AMN}\)と\(\triangle\mathrm{ABC}\)が相似であり,相似比が\(1 : 2\)であることを証明します。 まず条件から次が成り立ちます。
これを繋げると,次が成り立ちます。
また\(\angle\mathrm{A}\)が共通ですから,\(2\)組の辺の比とその間の角が等しいので,\(\triangle\mathrm{AMN}\)と\(\triangle\mathrm{ABC}\)は相似です。 相似比は\(\mathrm{AM} : \mathrm{AB} = 1 : 2\)です。
したがって,\(\angle\mathrm{AMN} = \angle\mathrm{ABC}\)ですから,同位角が等しいため\(\mathrm{BC} /\!/ \mathrm{MN}\)です。 また相似比より,\(\mathrm{BC} = 2 \mathrm{MN}\)です。
中点連結定理の逆も成り立ちます。 つまり,\(\triangle\mathrm{ABC}\)の辺\(\mathrm{AB}\),\(\mathrm{AC}\)上にそれぞれとった点\(\mathrm{M}\),\(\mathrm{N}\)が次を満たすとき,\(\mathrm{M}\)は辺\(\mathrm{AB}\)の,\(\mathrm{N}\)は辺\(\mathrm{AC}\)の中点です。
- \(\mathrm{BC} /\!/ \mathrm{MN}\)
- \(\mathrm{BC} = 2 \mathrm{MN}\)
証明は省略しますが,簡単なので確認してみてください。 三角形の相似を証明し,相似比を求めるだけです。
確認問題
次の(1)~(5)のうち,二等辺三角形の合同条件として適切なものをすべて挙げてください。
-
底辺以外の\(2\)辺がそれぞれ等しい。
-
頂角と底辺がそれぞれ等しい。
-
底辺と底角がそれぞれ等しい。
-
頂角と底辺以外の\(1\)辺がそれぞれ等しい。
-
底角と底辺以外の\(1\)辺がそれぞれ等しい。
答え
三角形の合同条件を満たすかどうかをそれぞれ順に確認していきます。
-
底辺以外の\(2\)辺が等しくても,頂角が違えば異なる三角形です。 したがって,合同条件にはなりません。
次の図を見てください。 円の中心と円周上にとった点で\(\triangle\mathrm{OAB}\)と\(\triangle\mathrm{OCD}\)をつくりました。
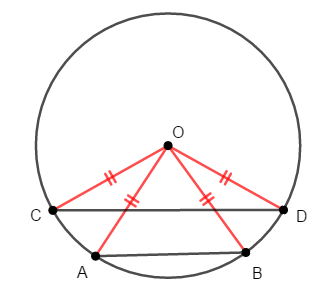
赤線は円の半径ですべて等しい長さですから,\(\triangle\mathrm{OAB}\)と\(\triangle\mathrm{OCD}\)はどちらも二等辺三角形です。 しかし見ての通り合同ではありません。 頂角が異なるからですね。
このように,底辺以外の\(2\)辺がそれぞれ等しくても,二等辺三角形が合同であるとはいえません。 そもそも底辺以外の\(2\)辺は等しいのですから,この条件では情報が\(1\)つだけしかなく,足りないわけですね。
-
これは合同条件になります。 二等辺三角形の頂角が分かれば,底角も分かります。 底角は等しいので,「\((180^{\circ} - \)頂角\() \div 2\)」で求められるわけです。
したがって,底辺と底角がそれぞれ等しいことになり,\(1\)辺とその両端の角がそれぞれ等しいので,合同条件を満たしています。
-
これは合同条件になります。 底辺と底角がそれぞれ等しければ,\(1\)辺とその両端の角がそれぞれ等しいので,合同条件を満たしています。
-
これは合同条件になります。 底辺以外の\(2\)辺は等しいですから,底辺以外の\(1\)辺がそれぞれ等しければ,頂角をはさむ\(2\)辺が両方ともそれぞれ等しいことになります。
したがって,\(2\)辺とその間の角がそれぞれ等しいので,合同条件を満たしています。
-
これは合同条件になります。 (4)と同じく,底辺以外の\(1\)辺が等しければ,頂角をはさむ\(2\)辺がそれぞれ等しくなります。
また底角が分かれば,頂角も分かります。 底角は等しいので,「\(180^{\circ} - 2 \times\)底角」で求められるわけです。
したがって,\(2\)辺とその間の角がそれぞれ等しいので,合同条件を満たしています。
以上より,二等辺三角形の合同条件として適切なものは,(2),(3),(4),(5)です。
平行四辺形\(\mathrm{ABCD}\)の対角線の交点を\(\mathrm{P}\)とするとき,次を証明してください。 ただし,平行四辺形の対角線がそれぞれの中点で交わることは利用しないでください。
-
\(\triangle\mathrm{ABD}\)と\(\triangle\mathrm{DCB}\)は合同である。
-
\(\triangle\mathrm{APD}\)と\(\triangle\mathrm{CPB}\)は合同である。
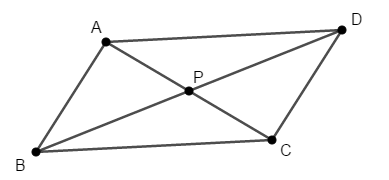
答え
合同条件を満たすことを確認していきます。
-
平行四辺形の対辺同士・対角同士は等しいですから,次が成り立ちます。
\( \begin{align} \mathrm{AD} &= \mathrm{CB} \\[5pt] \mathrm{AB} &= \mathrm{CD} \\[5pt] \angle\mathrm{BAD} &= \angle\mathrm{DCB} \end{align} \)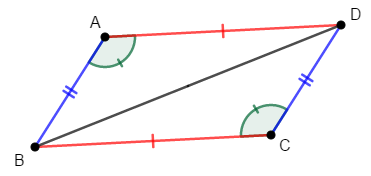
したがって,\(2\)辺とその間の角がそれぞれ等しいので,\(\triangle\mathrm{ABD}\)と\(\triangle\mathrm{DCB}\)は合同です。
-
辺\(\mathrm{AD}\)と\(\mathrm{BC}\)は平行ですから,錯角同士は等しいです。 また,対辺同士は等しいですから,次が成り立ちます。
\( \begin{align} \angle\mathrm{PAD} &= \angle\mathrm{PCB} \\[5pt] \angle\mathrm{PDA} &= \angle\mathrm{PBC} \\[5pt] \mathrm{AD} &= \mathrm{CB} \end{align} \)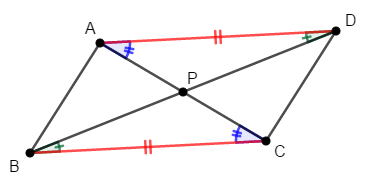
したがって,\(1\)辺とその両端の角がそれぞれ等しいので,\(\triangle\mathrm{APD}\)と\(\triangle\mathrm{CPB}\)は合同です。
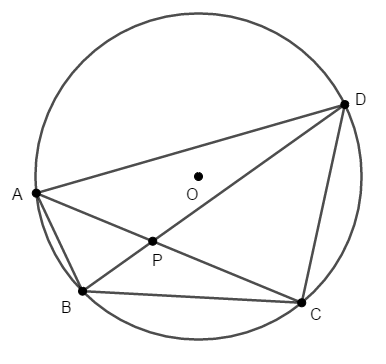
円\(\mathrm{O}\)の周上に次図のように点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\),\(\mathrm{D}\)をとります。
このとき,\(\triangle\mathrm{PAD}\)と\(\triangle\mathrm{PBC}\)が相似であることを証明してください。
答え
相似を証明する問題ですが,辺の比の情報はないので,\(2\)組の角がそれぞれ等しいことを証明します。 円に関する問題で等しい角といったら,円周角の定理です。
弧\(\mathrm{AB}\)に対する円周角が等しいので,\(\angle\mathrm{ADB} = \angle\mathrm{ACB}\)であり,弧\(\mathrm{CD}\)に対する円周角が等しいので,\(\angle\mathrm{CAD} = \angle\mathrm{CBD}\)です。
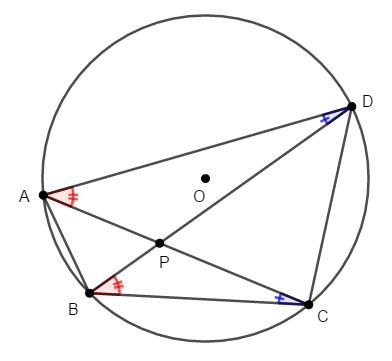
これで\(\angle\mathrm{ADP} = \angle\mathrm{BCP}\),\(\angle\mathrm{DAP} = \angle\mathrm{CBP}\)が成り立つことが分かりました。 したがって,\(2\)組の角がそれぞれ等しいので,\(\triangle\mathrm{PAD}\)と\(\triangle\mathrm{PBC}\)は相似です。
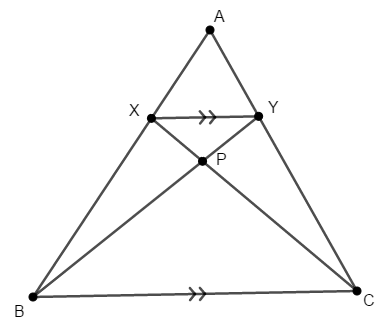
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{AB}\),\(\mathrm{AC}\)上にそれぞれ点\(\mathrm{X}\),\(\mathrm{Y}\)を,\(\mathrm{BC} /\!/ \mathrm{XY}\)を満たすようにとります。 また線分\(\mathrm{BY}\)と\(\mathrm{CX}\)の交点を\(\mathrm{P}\)とします。
\(\mathrm{AX} : \mathrm{XB} = 1 : 2\)であるとき,\(\mathrm{XP} : \mathrm{PC}\)を求めてください。
答え
線分の長さの比を求めるには,その線分を辺とする三角形の相似比を考えれば良いです。 \(\mathrm{BC} /\!/ \mathrm{XY}\)なので錯角が等しいことから,次が成り立ちます。
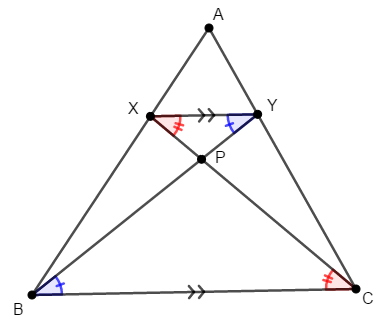
したがって,\(2\)組の角がそれぞれ等しいので\(\triangle\mathrm{PXY}\)と\(\triangle\mathrm{PCB}\)は相似です。 相似な三角形の対応する辺の比は等しいので,次が成り立ちます。
これで線分\(\mathrm{XY}\)と\(\mathrm{BC}\)の長さの比を考えればよくなりました。 この比も三角形の相似関係から考えます。 \(\mathrm{BC} /\!/ \mathrm{XY}\)なので同位角が等しいことから,次が成り立ちます。
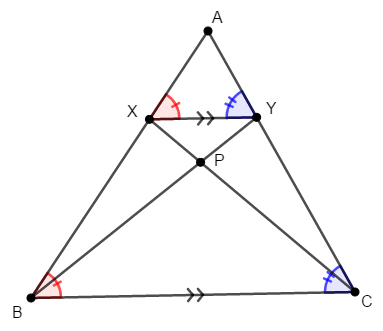
したがって,\(2\)組の角がそれぞれ等しいので\(\triangle\mathrm{AXY}\)と\(\triangle\mathrm{ABC}\)は相似です。 相似な三角形の対応する辺の比は等しいので,次が成り立ちます。
問題の条件より\(\mathrm{AX} : \mathrm{XB} = 1 : 2\)ですから,\(\mathrm{AX} = a\)とすると\(\mathrm{XB} = 2a\)です。 よって,\(\mathrm{AX} : \mathrm{AB}\)が求められます。
以上より,\(\mathrm{XP} : \mathrm{PC}\)は次の通りです。
