これからしばらく平面図形を解説していきますが,まずは中学校で学んだ内容の復習から始めます。 角・多角形・円といった基本的な図形の性質の確認から始めましょう。
本当は全て証明していきたいところですが,長くなってしまいますし,既に中学で扱った内容ですから割愛します。
目次
直線
まず,直線・線分・半直線について確認しておきます。 これらの使い分けができるようにしておきましょう。
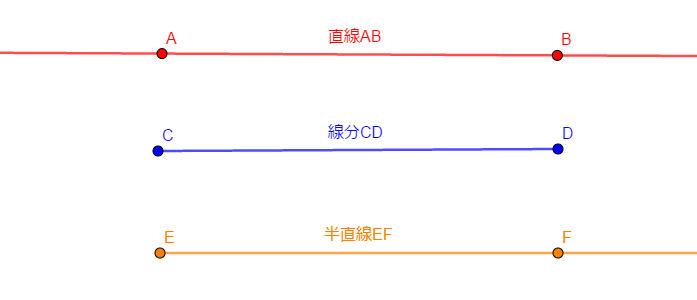
どれもまっすぐな線なのですが,直線には端がなく,両側で無限に続きます。 それに対して,線分には両端があります。 例として上図に直線\(\mathrm{AB}\),線分\(\mathrm{CD}\)を載せています。 それぞれ直線\(\mathrm{BA}\),線分\(\mathrm{DC}\)と表しても構いません。
また,半直線は片側だけ端があり,もう片側は無限に続きます。 例として上図に半直線\(\mathrm{EF}\)を載せています。 これは\(\mathrm{FE}\)とは表せません。 必ず端のある側から書いて表します。
例えば三角形の辺は線分であり,直線ではありません。 定義域を実数全体とする関数\(y = x\)のグラフは直線であり,線分ではありません。 定義域を\(0\)以上の実数全体とする関数\(y = x\)のグラフは半直線であり,直線ではありません。
角
では角に関する性質を見ていきましょう。
角について,次が成り立つ。
- 対頂角は等しい。
- \(1\)つの直線が平行な\(2\)直線と交わるとき,同位角は等しい。 逆も成り立ち,重要。
- \(1\)つの直線が平行な\(2\)直線と交わるとき,錯角は等しい。 逆も成り立ち,重要。
対頂角の確認からしましょう。 次図のように,\(2\)直線が交われば,そこに角ができますね。
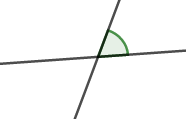
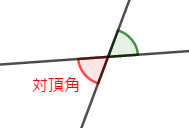
このとき,次の緑・赤の角のように向かい合う角を対頂角といいます。 対頂角は等しいです。
次に同位角・錯角について確認します。 \(1\)本の直線が\(2\)本の直線と交わるとき,次図のように\(2\)つの交点ができ,それぞれで角を考えられます。
このとき,次図の同じ色の角同士のように,同じ側にある角を同位角といいます。
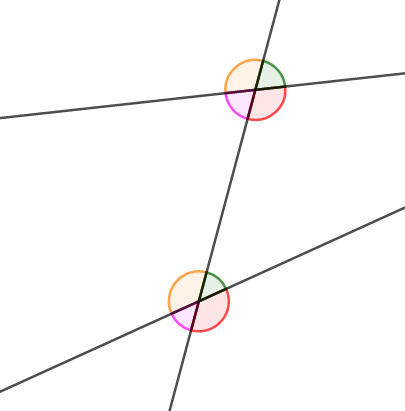
また,次図の同じ色の角同士は錯角といいます。 互いに反対側の位置にあり,ちょうど同位角の対頂角が錯角です。
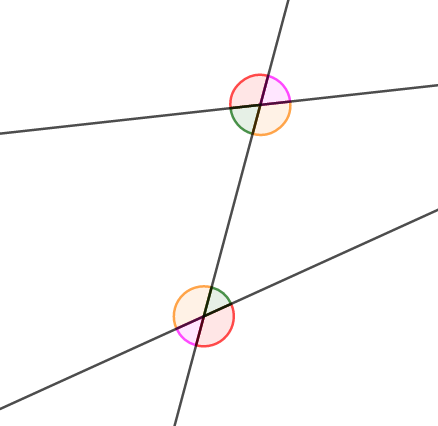
たまに誤解されますが,同位角・錯角は,\(1\)直線が交わる\(2\)直線が平行でない場合にも使う言葉です。 上図はまさにその例ですね。
この後確認するように,\(1\)直線が交わる\(2\)直線が平行である場合には,同位角同士,錯角同士は等しくなります。 その印象が強いからか,平行な場合のみに使う言葉だという誤解が見られます。
同位角・錯角が重要な役割を果たすのは,次のように\(1\)直線が交わる\(2\)直線が平行である場合です。 ここでは平行な\(2\)直線を\(\ell\),\(\mathcal{m}\)とし,緑の角に対する同位角・錯角も示してあります。
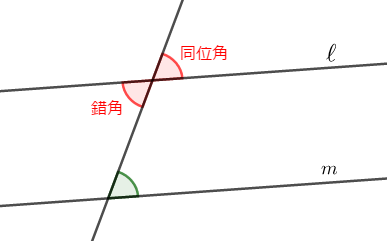
このとき,同位角同士,錯角同士は等しいです。 しかも逆も成り立ちます。 つまり,同位角が等しい,または錯角が等しいことが分かれば,直線\(\ell\)と\(\mathcal{m}\)が平行であることも分かります。
三角形
次は三角形に関する性質を確認していきます。 三角形は\(3\)つの辺・角を持つ図形ですね。
三角形について,次が成り立つ。
- 内角の和は\(180^{\circ}\)である。
- 外角は,それと隣り合わない\(2\)つの内角の和に等しい。
三角形の内角の和は,いつも\(180^{\circ}\)です。 これを少し確認してみましょう。
\(3\)つの内角に次のように色を付けておきます。 これらの和が\(180^{\circ}\)になることを確認しましょう。
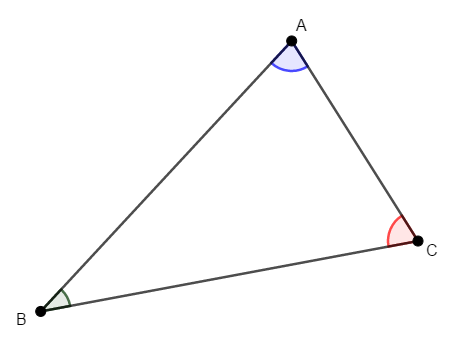
角度の合計を考えるのですから,\(3\)つの角を\(1\)箇所に集めて考えれば良いです。 次のように辺\(\mathrm{BC}\)を点\(\mathrm{C}\)の側に延長し,点\(\mathrm{C}\)を通り辺\(\mathrm{AB}\)と平行な直線を補助線として引きます。
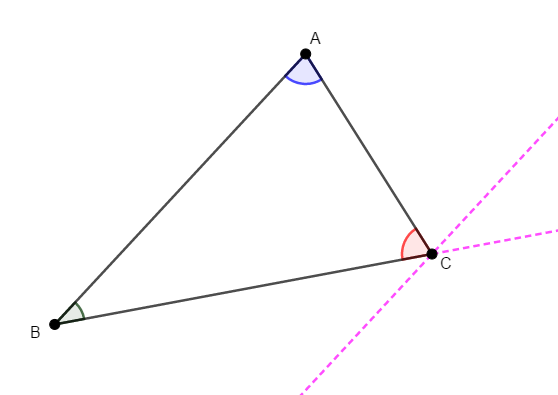
なぜこんな補助線を引くかといえば,「角の移動」のためです。 前項で学んだ通り,平行線を引くことで,青・緑の角と等しい同位角や錯角を見つけることができます。 次図の青い角は等しい錯角であり,緑の角は等しい同位角です。
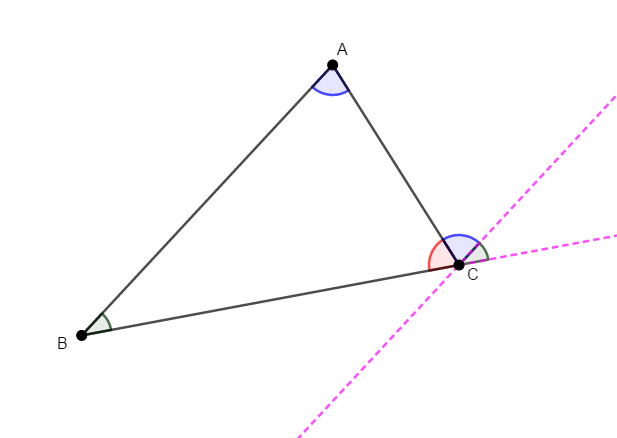
これで内角が\(1\)箇所に集まり,その和がちょうど半周分である\(180^{\circ}\)になることが分かりました。
さらにこの図を眺めると,角\(\mathrm{C}\)の外角が,ちょうど青と緑の角の和になっていることが分かります。 つまり,外角はそれと隣り合わない\(2\)つの内角の和に等しいわけです。
特別な三角形についても確認しておきましょう。 まずは二等辺三角形と正三角形です。
二等辺三角形・正三角形は次の性質を持つ。
- 【定義】二等辺三角形は,\(2\)辺の長さが等しい三角形である。
- 二等辺三角形の\(2\)つの底角は等しい。 逆も成り立ち,重要。
- 二等辺三角形の頂角の二等分線は,底辺を垂直に\(2\)等分する。 逆も成り立つ。
- 【定義】正三角形は,\(3\)辺の長さが等しい三角形である。
- 正三角形の内角は全て等しい。 逆も成り立ち,重要。
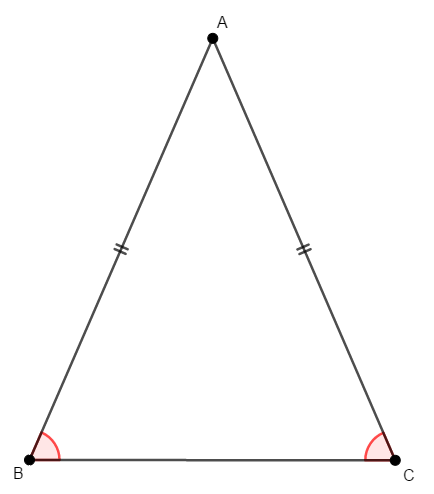
二等辺三角形は次のように\(2\)辺の長さが等しい三角形です。 等しい\(2\)辺の間の角を頂角,他\(2\)つの角を底角といいます。 底角と底角の間の辺は底辺です。
二等辺三角形の底角は,図の通り等しいです。 逆も成り立ち,底角が等しい三角形は,二等辺三角形です。
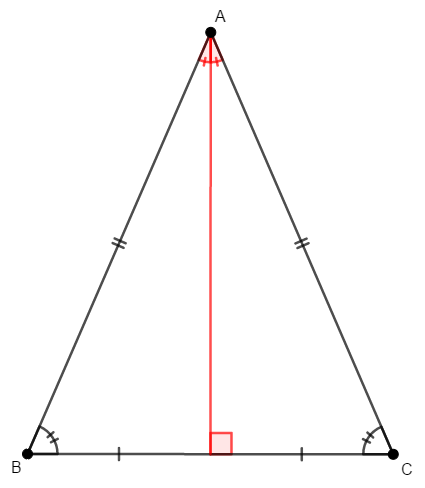
二等辺三角形の頂角を二等分する直線は,次図のように底辺を垂直に\(2\)等分します。 逆も成り立ち,二等辺三角形の底辺の垂直二等分線は,頂角を\(2\)等分します。
正三角形についても確認しておきましょう。 これは簡単な図形で,\(3\)辺の長さが等しい三角形です。
正三角形の内角は全て等しくなります。 逆も成り立ち,内角が全て等しい三角形は,正三角形です。
直角三角形についても確認しておきましょう。 直角三角形は直角の内角をもつ三角形ですが,次の性質が重要です。
次のような角\(\mathrm{C}\)を直角とする直角三角形\(\mathrm{ABC}\)を考える。
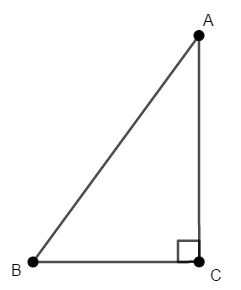
この直角三角形について,次が成り立つ。
特に次の\(3\)つの直角三角形は,\(3\)辺の長さの比がよく知られています。 覚えておきましょう。
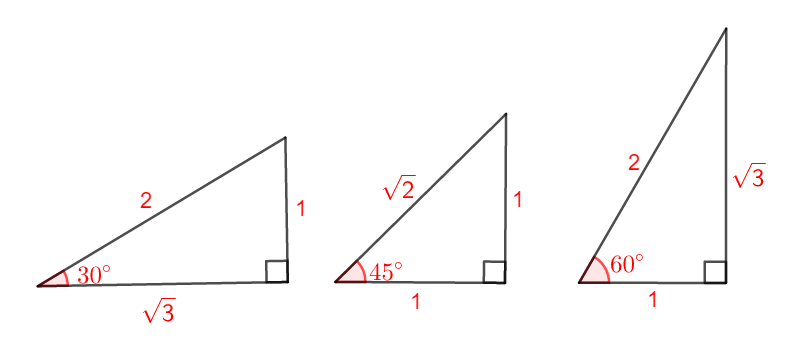
いずれにしても,三平方の定理が成り立っていることが分かると思います。
四角形
次は四角形に関する性質を確認していきます。 まずは重要な四角形である平行四辺形について確認します。
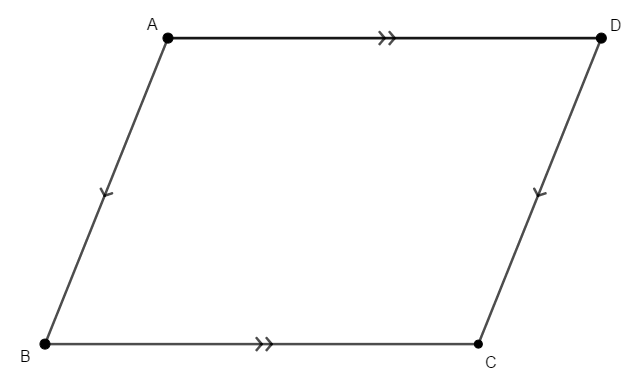
次のいずれかが成り立つ四角形は平行四辺形である。
- 【定義】\(2\)組の対辺がそれぞれ平行である。
- \(2\)組の対辺がそれぞれ等しい。
- \(2\)組の対角がそれぞれ等しい。
- \(1\)組の対辺が平行であり,長さが等しい。
- \(2\)本の対角線がそれぞれの中点で交わる。
また当然,平行四辺形はこれら全ての性質を持つ。
\(2\)組の対辺や\(2\)組の対角に注目すると,次の図のようになります。 対辺同士が等しい,または対角同士が等しい四角形は平行四辺形です。
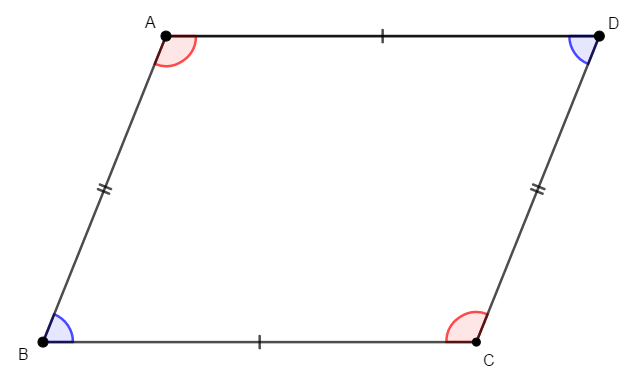
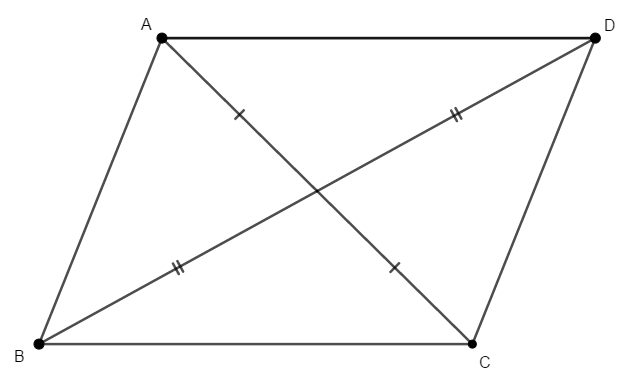
また,対角線がそれぞれの中点で交わる次のような四角形も,平行四辺形です。 他\(4\)つの条件ほど直観的には分かりませんが,しっかり押さえておきましょう。
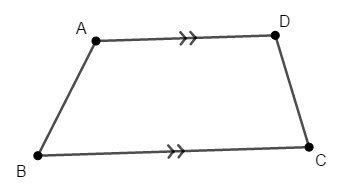
「\(2\)組の対辺がそれぞれ平行である四角形」は平行四辺形ですが,「\(1\)組の対辺が平行である」ことだけを定義とする四角形を台形といいます。
平行四辺形にもう少し条件を足すと,さらに特別な四角形になります。
特別な条件を満たす平行四辺形として,次のものがある。
- 角が全て等しいとき,長方形と呼ぶ。
- 辺の長さが全て等しいとき,ひし形と呼ぶ。
- 長方形かつひし形であるとき,正方形と呼ぶ。
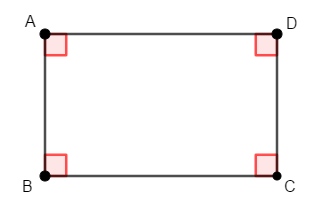
全ての角が等しいとき,平行四辺形は次図のようになり,これを長方形といいます。 全ての角は直角になります。
全ての辺の長さが等しいとき,平行四辺形は次図のようになり,これをひし形といいます。
全ての角と辺の長さが等しいとき,平行四辺形は次図のようになり,これを正方形といいます。 もちろん全ての角は直角です。
長方形・ひし形について,対角線に関する性質があります。 確認しておきましょう。
長方形・ひし形について,次が成り立つ。
- 長方形の対角線の長さは等しい。 一般に逆は成り立たない。
- ひし形の対角線は垂直に交わる。 一般に逆は成り立たない。
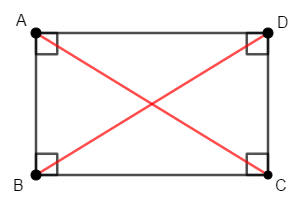
長方形の対角線を図示すると,次のようになります。 その長さは等しいです。
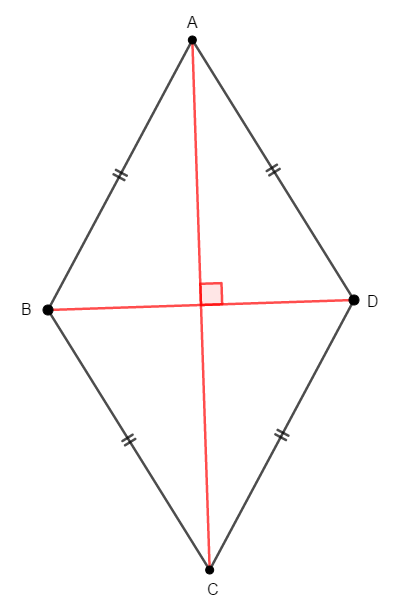
ひし形の対角線を図示すると,次のようになります。 それらは垂直に交わります。
この長方形・ひし形の対角線に関する性質の逆は,一般には成り立ちません。 しかし,平行四辺形の場合に限れば,逆も成り立ちます。
平行四辺形が次の条件を満たすとき,長方形やひし形になる。
- 対角線の長さが等しいならば,長方形である。
- 対角線が垂直に交わるならば,ひし形である。
四角形を含む多角形について,もうひとつ次のことを確認しておきます。
\(n\)角形の内角の和は,次の通りになる。
また,\(n\)角形の外角の和は,\(n\)によらず次の通りになる。
この内角の和の式が凸多角形(全ての内角が\(180^{\circ}\)未満)について成り立つことは,次図のように多角形を三角形に分割することで分かります。
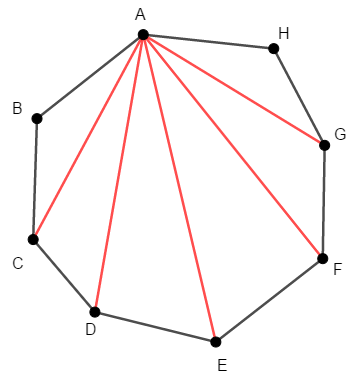
上図のように,凸\(n\)角形は\(n - 2\)個の三角形に分割できます。 下図を見れば分かる通り,この三角形の内角をすべて合わせると,元の多角形の内角の和が分かります。
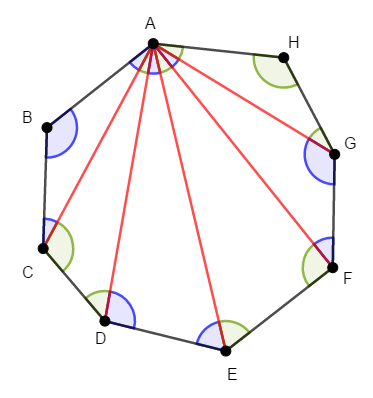
\(1\)つの三角形の内角の和が\(180^{\circ}\)であることを使えば,多角形の内角の和の公式が分かります。 外角の和については,確認問題としておきます。
円
円に関する性質を確認していきましょう。 まず円に関する用語を確認します。
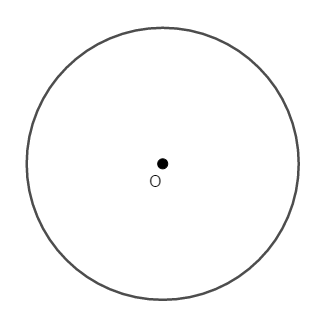
円とは,ある\(1\)点からの距離が等しい点の集まりです。 この基準となる\(1\)点を円の中心といいます。 次図の点\(\mathrm{O}\)は円の中心です。
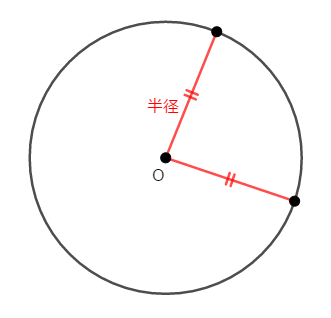
中心の周りの曲線は円周といいます。 円周上の点はすべて,円の中心との距離が等しいです。 この距離を円の半径といいます。
次図のように,円周上の点から円の中心を通って,反対側の円周まで引いた線分を直径といいます。
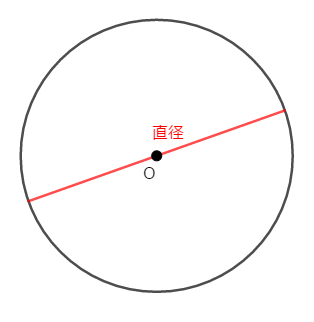
円周の長さは直径に比例することが知られています。 その比を円周率といい,\(\pi\)で表します。 円周率はどの円でも一定で,次のような値です。
次図の赤い部分のように,円周の一部を弧(円弧)といいます。 この図の弧は弧\(\mathrm{AB}\)であり,\(\stackrel{\huge\frown}{\mathrm{AB}}\)と表します。
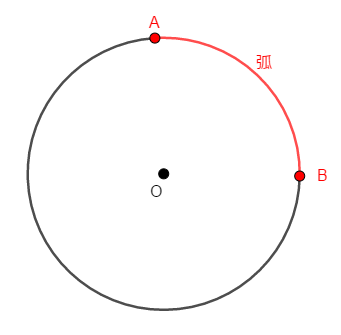
円周の一部を弧というのなら,上図の黒い部分だって弧\(\mathrm{AB}\)じゃないか!と思うかもしれません。 実際,それは正しいです。
弧の端点を決めると,上図の赤部分のような短い弧(劣弧)と黒部分のような長い弧(優弧)ができます。 どちらも弧\(\mathrm{AB}\)なのですが,数学の解答を書くときは,どちらか分かるようにしましょう。
ここでは,本文では基本的に劣弧を考え,補足で優弧の場合を見ることにします。
また,円周上に両端点をもつ線分を弦といいます。 先ほどの図に弦\(\mathrm{AB}\)を青色で追加すれば,次のようになります。
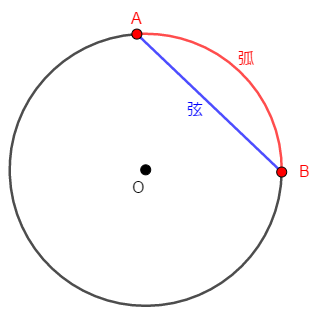
弧と弦に対して,次が成り立ちます。
長さの等しい弧に対する弦の長さは等しい。 逆は成り立たない。
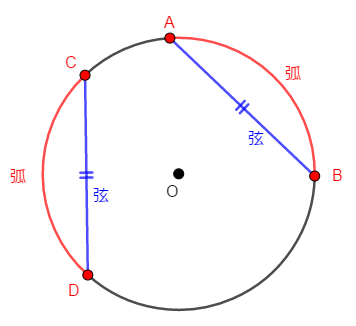
これが成り立つのは納得できますね。 逆が成り立たないのは,弦に対する弧には劣弧と優弧があるからです。
次が成り立つことも押さえておきましょう。
円の弦に対して,次が成り立つ。
- 円の中心と直径でない弦の中点を通る直線は,この弦に垂直である。
- 円の中心から直径でない弦に下ろした垂線は,この弦を\(2\)等分する。
- 直径でない弦の垂直二等分線は,円の中心を通る。
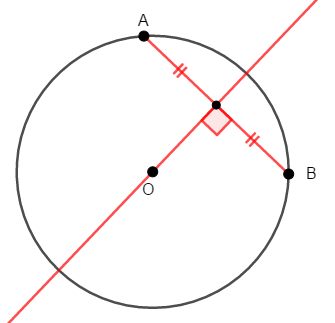
この性質を文字だけで見るとややこしそうですが,どれも上図の状況です。 何が仮定で何が結論なのかが少しずつ違うだけですね。
弦の垂直二等分線が必ず円の中心を通るという事実は,あまり印象にないかもしれませんが,特に作図などで役立ちます。 覚えておきましょう。
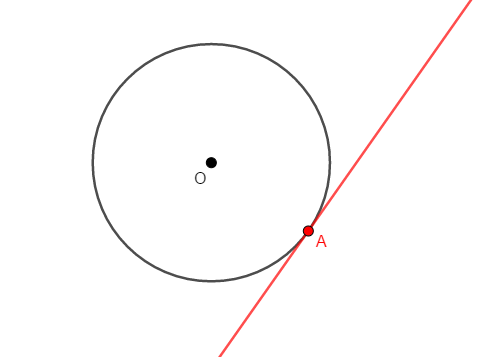
もうひとつ,接線について確認しておきましょう。 円の接線とは次の図のように,円と\(1\)点だけを共有する直線です。 共有する\(1\)点(下図では点\(\mathrm{A}\))を接点といいます。
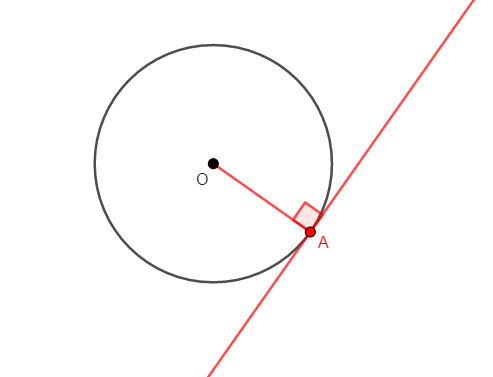
円と接線について,次が成り立つことを思い出しましょう。
円の接線は,その接点を通る半径(直径)に垂直である。
逆も成り立ち,円周上の点を通る直線が,その点を通る半径(直径)に垂直であるとき,この直線はこの円の接線である。
ざっくり理解するなら,接線を弦の特殊バージョンだと考えてみましょう。 弦の中点を通る半径(直径)は,その弦に垂直でしたね。 この弦を少しずつ円の中心から遠ざけていくと,接線に近くなります。
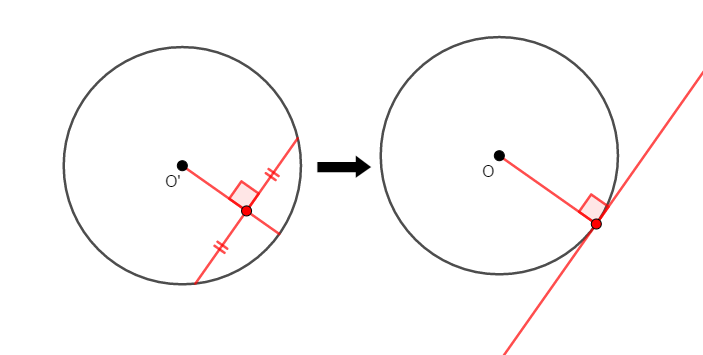
弦がほぼ接線になったとき,弦の中点は接点になったと考えられます。 だから接線は,接点を通る半径(直径)と垂直であると考えられるのです。
中心角と円周角
弧や弦の両端は円周上の点です。 この\(2\)点から\(2\)つの半径を考えると,次図のようにその間に角ができます。 これを中心角といいます。 特にこの図の中心角は,弧\(\mathrm{AB}\)に対する中心角や弦\(\mathrm{AB}\)に対する中心角といいます。
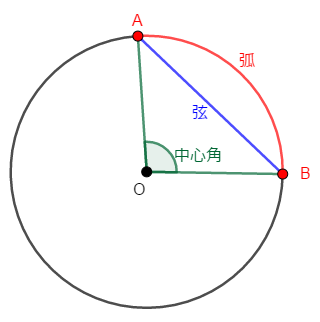
上の図は劣弧に対する中心角ですが,優弧に対する中心角も考えられます。
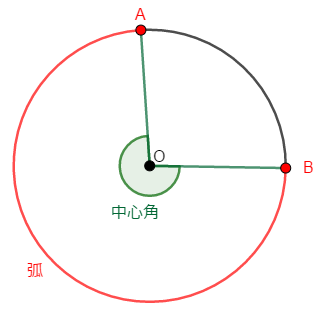
中心角について,次が成り立ちます。
弧の長さは,それに対応する中心角に比例する。
中心角によって円周が分割されるイメージができれば,納得のいく内容だと思います。 ここから,等しい円周角に対する弧の長さが等しいことや,長さの等しい弧に対する円周角が等しいことも分かります。
円周上の\(2\)点(弧や弦の両端など)から中心に線分を引けば中心角ができます。 それに対して,弧\(\mathrm{AB}\)を除く円周上の\(1\)点に線分を引けば,円周角ができます。 これを弧\(\mathrm{AB}\)に対する円周角や弦\(\mathrm{AB}\)に対する円周角といいます。
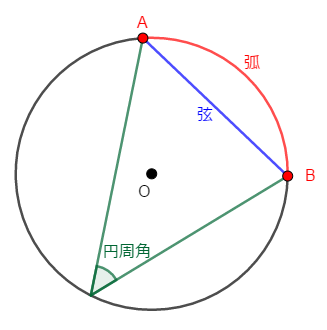
上で説明した「弧に対する円周角」は,弧上以外の円周上に\(1\)点をとるものでした。 しかし円周角の本来の定義的には,弧上に\(1\)点をとっても良さそうです。 教科書にも「弧上以外から」という文言はないことが多いです。
しかし,多くの教科書・参考書では,暗黙の内に「弧上以外の円周上から\(1\)点をとる」ことになっています。 ここで説明したような円周角の理解をしておいた方が,混乱せずに済むでしょう。
上の図は劣弧に対する円周角ですが,優弧に対する円周角も考えられます。
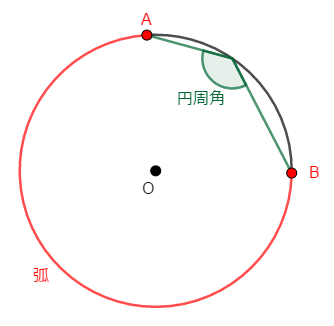
円周角と中心角に関しては,次の円周角の定理が重要です。
円周角と中心角について,次が成り立つ。
① \(1\)つの弧に対する円周角は一定である。

② \(1\)つの弧に対する円周角は,中心角の半分の大きさである。
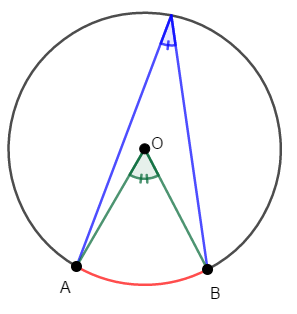
円周角の定理は非常に重要ですから,忘れないようにしましょう。
この内容は,先ほどの補足の通り,弧に対する円周角をとるときに,弧上以外から円周上の\(1\)点を選ぶことを前提とした書き方です。 もし弧上から\(1\)点を選んで円周角をとった場合,同じ弧に対しても円周角が等しいとは限りません。
下図のように,\(1\)点を弧上にとるか他の円周上にとるかで円周角は変わります。 円周角の定理を使うときに,円周角のとりかたを間違えないように気を付けましょう。
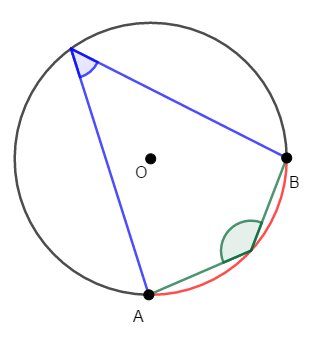
円周角の定理の逆も成り立ちます。 ざっくりいえば,\(4\)点からできる円周角(にあたる角)が等しければ,これらの点が同一円周上にあるという内容です。
\(2\)点\(\mathrm{X}\),\(\mathrm{Y}\)が直線\(\mathrm{AB}\)に対して同じ側にあり,次が成り立つとき,\(4\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{X}\),\(\mathrm{Y}\)は同一円周上にある。
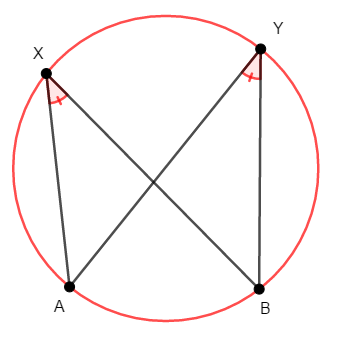
円周角の定理からも分かりますが,次の定理も成り立ちます。 この定理もまた重要です。
直径に対する円周角は直角である。 逆も成り立ち,重要。
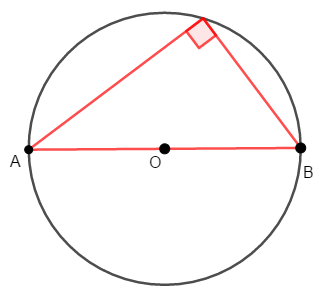
最後に,円の内部・周上・外部にある点について成り立つことを確認します。
円に弧\(\mathrm{AB}\)があり,直線\(\mathrm{AB}\)に対して同じ側に円内部の点\(\mathrm{I}\),円周上の点\(\mathrm{P}\),円外部の点\(\mathrm{E}\)があるとき,次が成り立つ。
- \(\angle\mathrm{AIB} > \angle\mathrm{APB}\)
- \(\angle\mathrm{AEB} < \angle\mathrm{APB}\)
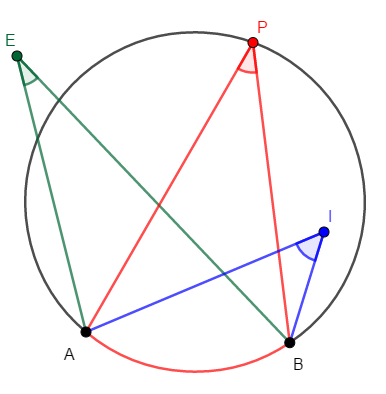
円周角の定理を思い出すと,円周角よりも中心角の方が大きかったですね。 このことからも,円の内部の方が大きい角度,円の外部の方が小さい角度になりそうと予想できます。
中学数学の復習を証明なしの詰め込み気味で進めました。 忘れていたことがあれば,ここでしっかり復習しておきましょう! なるべく証明の確認もしておくと,今後の練習にもなります。
確認問題
次の図で直線\(\mathrm{PQ}\),\(\mathrm{ZW}\)は平行です。 \(\angle\mathrm{BCZ}\)を求めてください。
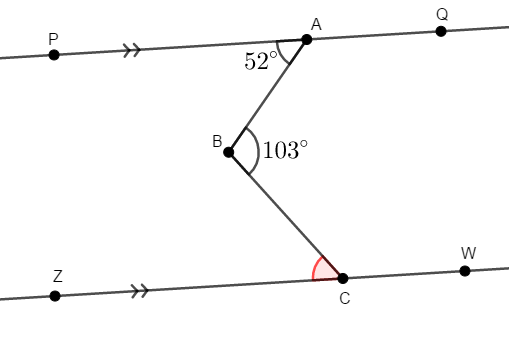
答え
平行線とそれに交わる線分がありますから,同位角や錯角が等しくなることを利用したいです。 しかし\(2\)本の平行線を横切る線は折れ線ですから,同位角や錯角が見当たりません。
そこで点\(\mathrm{B}\)を通り,直線\(\mathrm{PQ}\),\(\mathrm{ZW}\)と平行な直線\(\mathrm{XY}\)を引けば,折れ線をただの線分\(2\)本に分解できます。
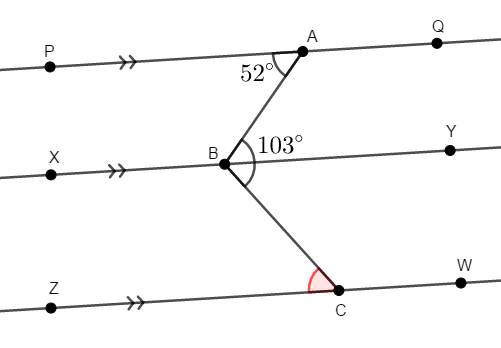
これで同位角や錯角を考えられます。 \(\angle\mathrm{PAB}\)と\(\angle\mathrm{YBA}\)は錯角同士なので,次が成り立ちます。
したがって,\(\angle\mathrm{YBC}\)も分かります。
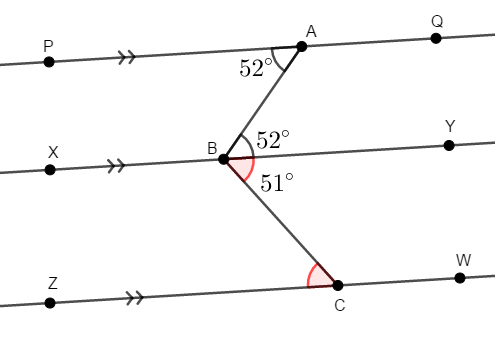
\(\angle\mathrm{YBC}\)と\(\angle\mathrm{BCZ}\)も錯角同士で等しいので,\(\angle\mathrm{BCZ}\)は次の通りになることが分かります。
\(n\)角形の内角の和が\(180^{\circ} \times (n - 2)\)であることを利用して,\(n\)角形の外角の和が\(360^{\circ}\)であることを証明してください。 (凸多角形だけの場合だけでOKです。)
答え
\(1\)つの頂点に注目すると,そこでの内角と外角の和は\(180^{\circ}\)です。 \(n\)角形には\(n\)個の頂点がありますから,全ての内角の和を\(S\),全ての外角の和を\(X\)とすると,次が成り立ちます。
この式は,頂点ごとに内角と外角を組み合わせて合計したと考えれば,理解できます。 内角の和の値は分かっていますから,外角の和は次のように求められます。
次の図において,四角形\(\mathrm{ABCD}\)は平行四辺形です。 点\(\mathrm{E}\)は,\(\angle\mathrm{ABC}\)の二等分線と\(\angle\mathrm{BCD}\)の二等分線の交点です。 \(\angle\mathrm{BEC}\)を求めてください。
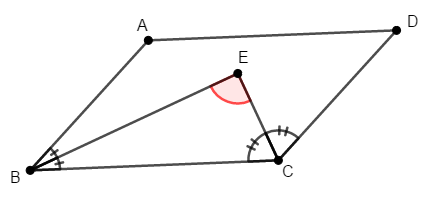
答え
具体的な角度の情報がありませんね。 とりあえず分かっている情報を使うために,二等分している角を次のようにおきましょう。
他に分かっている情報は,四角形\(\mathrm{ABCD}\)が平行四辺形であることです。 平行四辺形の対角は等しいですから,次が成り立ちます。
四角形の内角の和は\(360^{\circ}\)ですから,次が成り立ちます。
したがって,\(\triangle\mathrm{BEC}\)に注目すると,三角形の内角の和は\(180^{\circ}\)ですから,\(\angle\mathrm{BEC}\)が求められます。
次の図で,線分\(\mathrm{AC}\)は円\(\mathrm{O}\)の直径であり,\(\mathrm{BC} = \mathrm{BD}\)です。 \(\angle\mathrm{ADB}\)を求めてください。
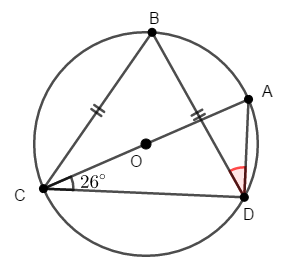
答え
とりあえず,円周角の定理で等しいことが分かる角を図示しておきます。 次図で同じ色の角は等しいです。
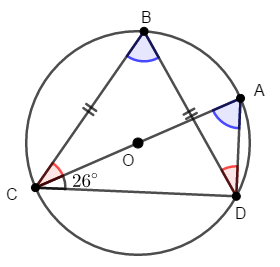
\(\angle\mathrm{ACB}\)と\(\angle\mathrm{ADB}\)は弧\(\mathrm{AB}\)に対する円周角,\(\angle\mathrm{CBD}\)と\(\angle\mathrm{CAD}\)は弧\(\mathrm{CD}\)に対する円周角なので等しいです。
また,線分\(\mathrm{AC}\)が直径であることから,タレスの定理により\(\angle\mathrm{ADC}\)が直角であることが分かります。 したがって,\(\triangle\mathrm{ADC}\)に注目すると,\(\angle\mathrm{CAD}\)が求められます。
先ほども確認した通り,円周角の定理により\(\angle\mathrm{CBD} = 64^{\circ}\)も成り立ちます。 これで二等辺三角形\(\mathrm{BCD}\)の頂角が分かりましたから,底角も分かります。 二等辺三角形の底角は等しいですから,次が成り立ちます。
これで円周角の定理より,\(\angle\mathrm{ADB} = 32^{\circ}\)であることが分かりました。
次の図で線分\(\mathrm{AB}\)と線分\(\mathrm{OC}\)は平行です。 \(\angle\mathrm{OCD}\)を求めてください。
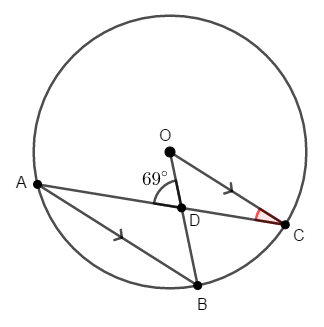
答え
\(\angle\mathrm{OCD} = x\)とします。
平行線とそれを横切る線分がありますから,同位角・錯角の確認をしておきます。 下図の赤い角同士・青い角同士は錯角同士であり,それぞれ等しいです。
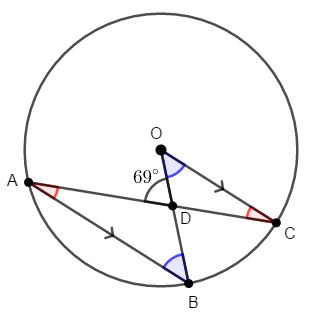
ここで\(\angle\mathrm{COB}\)が中心角であることに注目します。 それに対する弧は弧\(\mathrm{BC}\)です。
弧\(\mathrm{BC}\)に対する円周角を探すと,\(\angle\mathrm{BAC}\)があります。 したがって,赤い角は\(x\)ですから,円周角の定理により青い角が\(2x\)であることが分かります。 同じ弧に対する円周角と中心角の関係ですね。
\(\triangle\mathrm{COD}\)に注目すると,\(\angle\mathrm{ODA}\)はこの三角形の外角ですから,その角度はこの外角に隣り合わない内角の和に等しく,次が成り立ちます。
これで\(\angle\mathrm{OCD} = 23^{\circ}\)であることが分かりました。
