今回考えるのは,何らかの情報が与えられている場合の確率です。 例えば,明日の天気が晴れである確率を求めるとき,何も情報がない場合と直近の気象情報を知っている場合では異なる結果になるでしょう。
目次
条件付き確率
次図のように,箱の中に赤色または青色の玉が\(10\)個入っています。 玉には\(1\)~\(3\)のいずれかの番号が振られています。
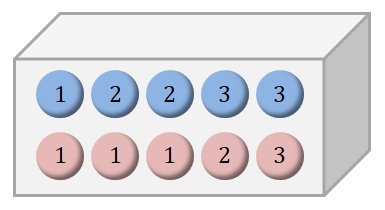
この箱から玉を\(1\)個取り出すとき,その玉の番号が\(2\)である確率はいくつでしょうか? 簡単な問いですね。 \(2\)の玉は\(3\)個あるので,この確率は次の通りです。
少しだけヒントを与えられた場合はどうでしょう? 取り出した玉が青色だと教えてもらった場合,その番号が\(2\)である確率を求めてみましょう。 青玉は\(5\)個あり,その内\(2\)の玉は\(2\)個ですから,この確率は次の通りです。
このように,ある事象が起こる確率を求めるとき,何らかの情報が与えられていれば,それを活用できます。 もう少し一般化して考えてみましょう。
事象\(\mathrm{A}\),\(\mathrm{B}\)に対して,事象\(\mathrm{A}\)が起こったことが分かっているときに事象\(\mathrm{B}\)が起こる確率を考えます。 これを事象\(\mathrm{A}\)における事象\(\mathrm{B}\)の条件付き確率といい,\(P_{\mathrm{A}}(\mathrm{B})\)または\(P(\mathrm{B} | \mathrm{A})\)で表します。
条件付き確率の記号をややこしく思うかもしれません。 しかし,これがあくまで\(\mathrm{B}\)の確率であることを考えれば,実はややこしくありません。
単純な\(\mathrm{B}\)の確率は\(P(\mathrm{B})\)と表しますね。 これに\(\mathrm{A}\)という条件を加えた確率を表すには,この記号のどこかに\(\mathrm{A}\)を入れる必要があります。
その\(1\)つの表現方法が\(P_{\mathrm{A}}(\mathrm{B})\)です。 括弧の前に小さく条件の事象\(\mathrm{A}\)を書いたものです。 そしてもう\(1\)つが\(P(\mathrm{B} | \mathrm{A})\)です。 集合の条件を表すときと同じように,\(\mathrm{B}\)の後ろに条件の事象\(\mathrm{A}\)を足したものです。
この確率は,事象\(\mathrm{A}\)が起こったことを前提としているので,全事象を\(\mathrm{A}\)として考えれば良いです。 そして\(\mathrm{A}\)を前提とした場合の事象\(\mathrm{B}\)とは,\(\mathrm{A} \cap \mathrm{B}\)のことですから,この条件付き確率は次の通りです。
理屈は簡単ですね。 上の式をただ暗記しようとしても難しいですが,理屈が分かれば大したことはありません。
乗法定理
前項で求めた条件付き確率を求める式をもう一度見てみましょう。
この右辺の分母分子を全事象の要素数で割ると,分母は事象\(\mathrm{A}\)が起こる確率,分子は積事象\(\mathrm{A} \cap \mathrm{B}\)が起こる確率になります。
これを少し変形した式が,確率の乗法定理と呼ばれるものです。
事象\(\mathrm{A}\),\(\mathrm{B}\)について,次が成り立つ。
この式をざっくり理解してみましょう。 \(P(\mathrm{A} \cap \mathrm{B})\)とは,事象\(\mathrm{A}\)も事象\(\mathrm{B}\)も起こる確率のことです。 それは,事象\(\mathrm{A}\)が起こり,その上で事象\(\mathrm{B}\)が起こるということです。
事象\(\mathrm{A}\)が起こる確率は\(P(\mathrm{A})\)で,「その上で」事象\(\mathrm{B}\)が起こる確率は\(P_{\mathrm{A}}(\mathrm{B})\)です。 これらの確率を掛け合わせたものが,事象\(\mathrm{A}\)も事象\(\mathrm{B}\)も起こる確率になっているわけですね。
乗法定理の活用
さっそく乗法定理を活用する問題を解いてみましょう。 \(10\)本のくじが入っている箱があり,その内\(2\)本だけがアタリ,残りはハズレです。 \(2\)人が順番にくじを引き,引いたくじは箱に戻さないものとします。
太郎君は\(2\)番目にくじを引きます。 太郎君「だけ」がアタリを引く確率を求めてみましょう。
\(1\)人目はハズレを引き,太郎君はアタリを引く必要がありますね。 \(1\)人目がハズレを引く事象を\(\mathrm{A}\),太郎君がアタリを引く事象を\(\mathrm{B}\)とすると,求めたいのは次の確率です。
乗法定理を使えば,この式は次のように変形できます。
\(P(\mathrm{A})\)は簡単に分かります。 くじが\(10\)本あり,その内\(8\)本がハズレですから,\(P(\mathrm{A})\)は次の通りです。
次に\(P_{\mathrm{A}}(\mathrm{B})\)を求めます。 事象\(\mathrm{A}\)が起こったことが前提ですから,くじは\(9\)本しかなく,その内\(2\)本だけがアタリです。 したがって,この条件付き確率は次の通りです。
これで太郎君がアタリを引く確率が,次のように求められます。
このくじの引き方のように,取り出したものを元に戻さない取り出し方を非復元抽出といいます。 条件付き確率の典型問題です。
確認問題
次図のように,箱の中に赤色または青色の玉が\(10\)個入っています。 玉には\(1\)~\(3\)のいずれかの番号が振られています。

この箱から玉を\(2\)個取り出す試行について,次の問いに答えてください。
-
取り出した玉の番号が同じである確率を求めてください。
-
取り出した玉が異なる色であった場合に,取り出した玉の番号が同じである確率を求めてください。
答え
何らかの情報が与えられることで,確率が変化する例の問題です。 条件付き確率の計算をマスターしましょう。
-
番号が\(1\)で一致する場合,\(2\)で一致する場合,\(3\)で一致する場合があります。 これらは互いに排反ですから,それぞれの場合で玉の番号が一致する確率の和を求めれば良いです。
例えば,取り出した玉の番号が両方とも\(1\)である確率は,\(4\)個ある\(1\)の玉から\(2\)個を取り出すということなので,次の通りです。
\( \begin{align} \displaystyle\frac{{}_4\mathrm{C}_2}{{}_{10}\mathrm{C}_2} \end{align} \)同様に取り出した玉の番号が両方とも\(2\)である場合,\(3\)である場合の確率も求められます。 したがって,題意の確率は次の通りです。
\( \begin{align} &\quad \displaystyle\frac{{}_4\mathrm{C}_2}{{}_{10}\mathrm{C}_2} + \displaystyle\frac{{}_3\mathrm{C}_2}{{}_{10}\mathrm{C}_2} + \displaystyle\frac{{}_3\mathrm{C}_2}{{}_{10}\mathrm{C}_2} \\[5pt] &= \displaystyle\frac{6 + 3 + 3}{45} \\[5pt] &= \textcolor{red}{\displaystyle\frac{4}{15}} \end{align} \) -
基本的な考え方は(1)と同じですが,取り出した玉の色が異なるので,同じ番号の選び方は青・赤から\(1\)個ずつという場合に限られます。 玉の番号がどの番号で一致する場合も互いに排反なので,題意の確率は次の通りです。
\( \begin{align} &\quad \displaystyle\frac{1 \times 3}{{}_{10}\mathrm{C}_2} + \displaystyle\frac{2 \times 1}{{}_{10}\mathrm{C}_2} + \displaystyle\frac{2 \times 1}{{}_{10}\mathrm{C}_2} \\[5pt] &= \displaystyle\frac{3 + 2 + 2}{45} \\[5pt] &= \textcolor{red}{\displaystyle\frac{7}{45}} \end{align} \)
箱の中にくじが\(10\)本入っており,その内\(2\)本はアタリ,残りはハズレです。 \(4\)人の人物が順番にくじを\(1\)本ずつ引き,引いたくじは箱に戻さないとします。
\(4\)人目にくじを引く人物がアタリを引く確率を求めてください。
答え
引いたくじを箱に戻さないので,\(4\)人目の前にアタリが\(2\)回引かれてはいけません。 したがって,初めの\(3\)人がアタリを引いて良いのは\(1\)回までです。 これを考慮すると,\(4\)人目がアタリを引ける事象は次の\(4\)通りです。
[1] 初めの\(3\)人がハズレを引く場合。 このとき\(4\)人目がアタリを引く確率は,次の通りです。
この計算では,確率の乗法定理を利用しています。 くじを引くたびにくじの本数が減ることに注意してください。 アタリ・ハズレの残り本数も減ります。
また,後の計算の都合上,約分を途中で止めています。
[2] 初めの\(3\)人のうち,\(1\)人目だけがアタリを引く場合。 このとき\(4\)人目がアタリを引く確率は,次の通りです。
[3] 初めの\(3\)人のうち,\(2\)人目だけがアタリを引く場合。 このとき\(4\)人目がアタリを引く確率は,次の通りです。
[4] 初めの\(3\)人のうち,\(3\)人目だけがアタリを引く場合。 このとき\(4\)人目がアタリを引く確率は,次の通りです。
これらの事象は互いに排反ですから,\(4\)人目がアタリを引く確率は,次の通りです。
ある数学・化学・物理学の研究者のグループを考えます。 その男女比は\(4 : 6\)です。 また,男女別の研究分野の割合は,次の通りです。
■ 男性の研究分野
| 研究分野 | 割合 [%] |
|---|---|
| 数学 | \(30\) |
| 化学 | \(40\) |
| 物理学 | \(30\) |
■ 女性の研究分野
| 研究分野 | 割合 [%] |
|---|---|
| 数学 | \(50\) |
| 化学 | \(30\) |
| 物理学 | \(20\) |
このグループからランダムに\(1\)人を選びます。 この試行について,次の問いに答えてください。
-
選んだ人が女性であったとき,その人の研究分野が数学である確率を求めてください。
-
選んだ人の研究分野が数学である確率を求めてください。
-
選んだ人の研究分野が数学であったとき,その人が女性である確率を求めてください。
答え
条件付き確率の問題ですが,なかなかややこしいです。 各事象を記号で表して整理しましょう。
選んだ人が男性であるという事象を\(\mathrm{M}\),女性であるという事象を\(\mathrm{F}\)と表します。 また,選んだ人の研究分野が数学であるという事象を\(\mathrm{m}\),化学であるという事象を\(\mathrm{c}\),物理学であるという事象を\(\mathrm{p}\)と表します。
-
求めたい確率は,\(P_{\mathrm{F}}(\mathrm{m})\)です。 特に計算することもなく,答えは問題文に書いてあります。
女性の内,数学を研究分野とする人は\(50\)%ですから,選んだ人が女性だと分かっている以上,その人の研究分野が数学である確率は次の通りです。
\( \begin{align} P_{\mathrm{F}}(\mathrm{m}) = \displaystyle\frac{50}{100} = \textcolor{red}{\displaystyle\frac{1}{2}} \end{align} \)同様に,問題文の条件を次のようにまとめられます。
\( \begin{align} P(\mathrm{M}) &= \displaystyle\frac{2}{5} \\[5pt] P(\mathrm{F}) &= \displaystyle\frac{3}{5} \\[5pt] P_{\mathrm{M}}(\mathrm{m}) &= \displaystyle\frac{3}{10} \\[5pt] P_{\mathrm{M}}(\mathrm{c}) &= \displaystyle\frac{2}{5} \\[5pt] P_{\mathrm{M}}(\mathrm{p}) &= \displaystyle\frac{3}{10} \\[5pt] P_{\mathrm{F}}(\mathrm{m}) &= \displaystyle\frac{1}{2} \\[5pt] P_{\mathrm{F}}(\mathrm{c}) &= \displaystyle\frac{3}{10} \\[5pt] P_{\mathrm{F}}(\mathrm{p}) &= \displaystyle\frac{1}{5} \end{align} \) -
求めたい確率は,\(P(\mathrm{m})\)です。 数学を研究している人の割合は,男性内での割合と女性内での割合しか分かっていません。 男性の場合と女性の場合に分けて考える必要がありそうです。
この研究者グループには男性と女性しかいません。 さらに「選んだ人が男性数学研究者」,「選んだ人が女性数学研究者」という\(2\)つの事象は排反ですから,次が成り立ちます。
\( \begin{align} P(\mathrm{m}) = P(\mathrm{M} \cap \mathrm{m}) + P(\mathrm{F} \cap \mathrm{m}) \end{align} \)確率の乗法定理を使えば,この続きを計算できます。
\( \begin{align} P(\mathrm{m}) &= P(\mathrm{M} \cap \mathrm{m}) + P(\mathrm{F} \cap \mathrm{m}) \\[5pt] &= P(\mathrm{M})P_{\mathrm{M}}(\mathrm{m}) + P(\mathrm{F})P_{\mathrm{F}}(\mathrm{m}) \\[5pt] &= \displaystyle\frac{2}{5} \cdot \displaystyle\frac{3}{10} + \displaystyle\frac{3}{5} \cdot \displaystyle\frac{1}{2} \\[5pt] &= \textcolor{red}{\displaystyle\frac{21}{50}} \end{align} \) -
求めたい確率は,\(P_{\mathrm{m}}(\mathrm{F})\)です。 確率の乗法定理を繰り返し使えば,機械的に計算できます。 途中で(2)の計算結果も使います。
\( \begin{align} P_{\mathrm{m}}(\mathrm{F}) &= \displaystyle\frac{P(\mathrm{F} \cap \mathrm{m})}{P(\mathrm{m})} \\[5pt] &= \displaystyle\frac{P(\mathrm{F})P_{\mathrm{F}}(\mathrm{m})}{P(\mathrm{m})} \\[5pt] &= \displaystyle\frac{\displaystyle\frac{3}{5} \cdot \displaystyle\frac{1}{2}}{\displaystyle\frac{21}{50}} \\[5pt] &= \displaystyle\frac{3}{5} \cdot \displaystyle\frac{1}{2} \cdot \displaystyle\frac{50}{21} \\[5pt] &= \textcolor{red}{\displaystyle\frac{5}{7}} \end{align} \)直感的には求めづらいですから,確率の乗法定理をしっかり使いこなせるようにしましょう。
