三角形に関する有名な定理であるチェバの定理,メネラウスの定理について学びましょう。 共点や共線の問題を考えるための道具にもなります。
目次
チェバの定理
さっそくチェバの定理の内容から見ていきましょう。
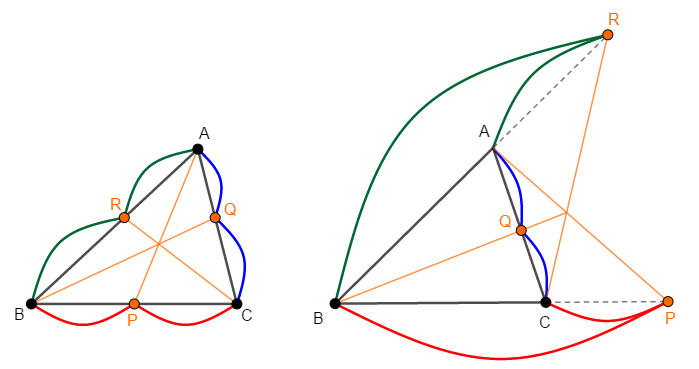
\(\triangle\mathrm{ABC}\)とその辺(とその延長)上にない\(1\)点\(\mathrm{X}\)について考える。 また,頂点と\(\mathrm{X}\)を結ぶ直線は,その対辺と交わるとする。
このとき,各頂点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)と\(\mathrm{X}\)を結ぶ直線がその対辺(とその延長)と交わる点をそれぞれ\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)とすると,次が成り立つ。
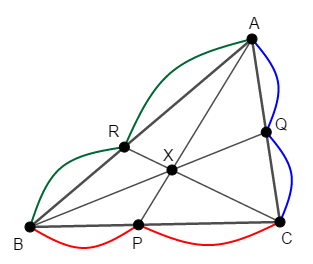
この式は簡単に覚えられます。 適当な頂点から始めて,三角形を一周しながら途中の線分の長さを分母・分子に交互に並べるだけです。
これは点\(\mathrm{X}\)が三角形の外部にあるときにも成り立ちます。
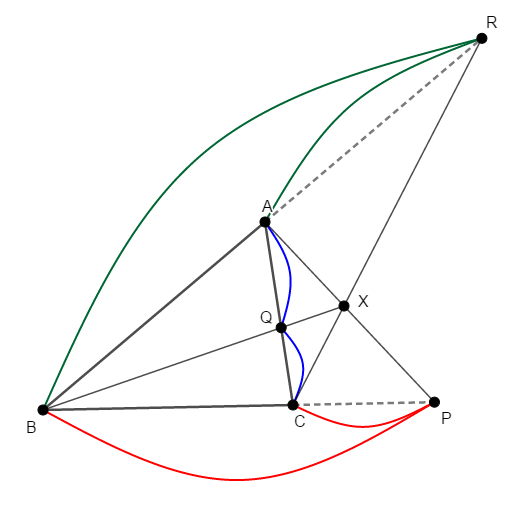
この場合の三角形の周りのなぞり方は,辺の端を一度飛び越えたりします。 一度\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)を中継するのです。
ではチェバの定理を証明しましょう。 線分の比に関する式を導きたいので,すぐ思い付くのは相似の利用です。 しかし,点\(\mathrm{X}\)は自由にとれる点ですし,図中に相似になりそうな三角形が見当たりません。
そこで利用するのが面積比です。 例えば\(\triangle\mathrm{XAB}\)と\(\triangle\mathrm{XCA}\)の面積比を考えてみます。
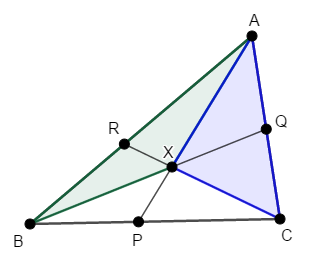
両者とも\(\mathrm{AX}\)を底辺と考えれば,底辺が等しいですから,面積比は高さの比(次図の赤い線の比)と等しいです。
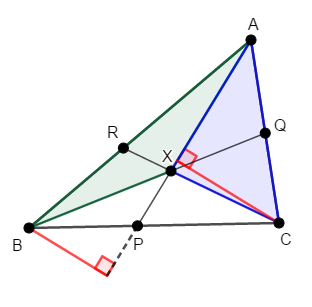
このとき,次図の赤い三角形は相似(\(2\)組の角がそれぞれ等しい)ですから,対応する辺の比が等しいため,上図の赤い線の比は\(\mathrm{BP}\)と\(\mathrm{PC}\)の比と等しくなります。

この比は\(\triangle\mathrm{XAB}\)と\(\triangle\mathrm{XCA}\)と等しかったのですから,次が成り立つことになります。
うまく面積の比と線分の比を繋げられました。 同様に\(\triangle\mathrm{XBC}\)と\(\triangle\mathrm{XAB}\)の面積比,\(\triangle\mathrm{XCA}\)と\(\triangle\mathrm{XBC}\)の面積比を考えれば,次が成り立つことも分かります。
これらの式をよく見ると,同じ三角形の面積が分母・分子に\(1\)つずつ現われますから,これらを辺々掛け合わせれば,三角形の面積比を打ち消して,線分の比だけが残ります。
これでチェバの定理が成り立つことを証明できました。 この定理は逆も成り立ち重要ですから,次項で確認します。
チェバの定理の逆
チェバの定理の逆は,次の内容です。 直線たちが共点であることを証明するために使えます。
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)とその延長上にそれぞれ点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)があるとする。 これが次の【条件】を全て満たすとき,\(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)は共点である。(\(1\)点で交わる。)
【条件】
① \(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)のうち,\(\triangle\mathrm{ABC}\)の辺上にあるのは,\(1\)点または\(3\)点である。
② \(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)のうち,\(2\)本が交わる。
③ 次の式が成り立つ。
嫌になるほどややこしいですね。 共点を示すためのチェック項目が\(3\)つもあります。 このややこしさは,\(3\)点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が三角形の辺の延長上にある場合も考慮しているからです。
\(3\)点が三角形の辺上にある場合だけを考慮するなら,もっとすっきりした定理になります。 この場合,条件①は当然満たされ,条件②が満たされることも,図をかいてみれば分かります。
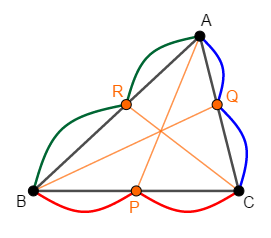
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)上にそれぞれある点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)を考える。
これが次の式を満たすとき,\(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)は共点である。
簡易版の方だけ覚えておけば事足りることも多いですが,やっぱり元の\(3\)条件ある方を理解しておいた方が,応用範囲も広がります。
とはいえ覚えるのが辛いです。 条件③はインパクトがあるのでまだ良いですが,条件①や②が記憶から抜け落ちそうです。
そこで,少なくとも次の図の形は頭の中に入れておきましょう。 チェバの定理もその逆も,次の図のような状況に関する定理です。 それを文字に起こすからややこしいのであって,図の状況自体はそこまで複雑ではありません。
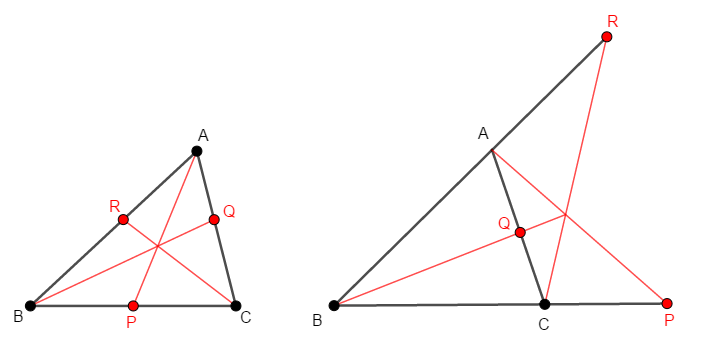
図を見れば,条件①の通り,辺上の点は\(1\)個(図右)か\(3\)個(図左)じゃないとダメだと分かります。
それでも条件②は,ピンと来ないかもしれません。 しかし条件①と③だけだと,次図のように②の直線が平行になってしまうことがあり,必要な条件なのです。 直線が平行だと共点にはなりません。
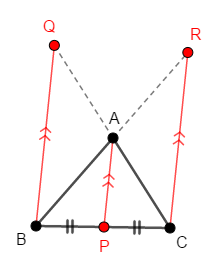
この図で条件①と③が成り立つことを確認しておいてください。
それでは,チェバの定理の逆を証明していきましょう。 条件①,②,③が成り立つことを前提に,\(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)が共点であることを示せば良いですね。
ここではチェバの定理をうまく活用しましょう。 チェバの定理もその逆も,想定する状況は似たようなものですからね。
数学Ⅰで命題とその逆の真偽は無関係であることを学びました。 そして定理は命題の一種ですから,このことは定理にも当てはまります。
ですからチェバの定理の逆を証明するために,チェバの定理を使うことには何の問題もありません。 逆同士という関係性はあるものの,その真偽は互いに独立しているからです。
まず条件①から,点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)のうち,少なくとも\(1\)点は三角形の辺上にあります。
どの点が辺上にあると想定しても同じことですから,点\(\mathrm{Q}\)が辺\(\mathrm{CA}\)上にあるとしましょう。 次図のいずれかの状況ですね。
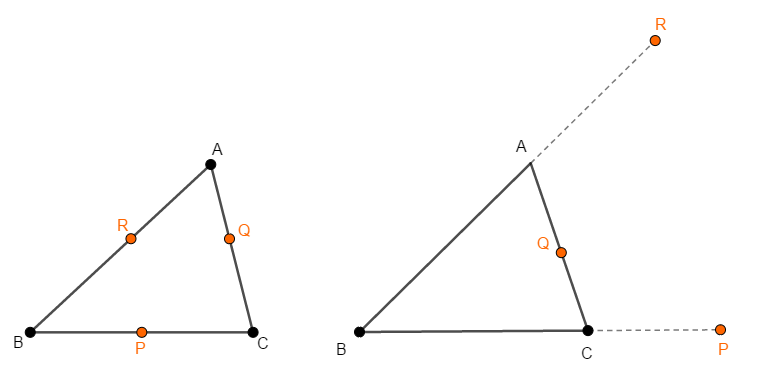
次に\(\mathrm{AP}\)と\(\mathrm{CR}\)の交点を\(\mathrm{X}\)とします。 あとは直線\(\mathrm{BX}\)と辺\(\mathrm{CA}\)の交点\(\mathrm{Q}'\)が\(\mathrm{Q}\)と一致することを示せば,証明完了です。
ここで「あれ?」と思った方は鋭いです。 \(\mathrm{AP}\)と\(\mathrm{CR}\)に交点がない,つまり平行である場合を考慮していませんね。 このことについては,一度証明の流れを最後まで見てから補足します。
さて,\(\mathrm{Q}\)と\(\mathrm{Q}'\)が一致することを示したいのですが,まずは点\(\mathrm{Q}'\)が,\(\mathrm{Q}\)と同じく辺\(\mathrm{CA}\)の内分点であることを確認しましょう。
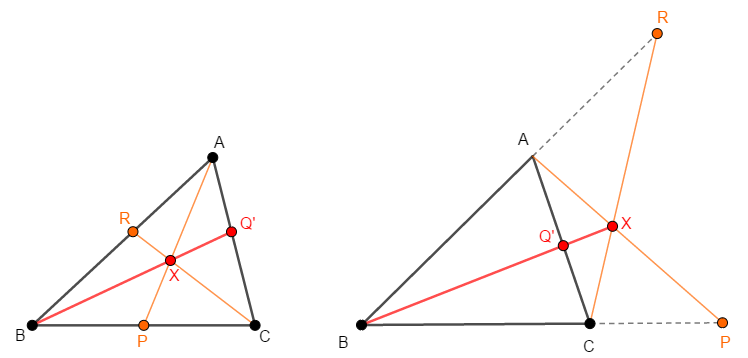
これは上図を見ての通り,点\(\mathrm{X}\)が\(\angle\mathrm{ABC}\)(またはその対頂角)内にあることから分かります。 右図で\(\mathrm{P}\)や\(\mathrm{Q}\)が反対側の延長上にある場合にも,これは成り立ちます。
これで点\(\mathrm{Q}'\)が辺\(\mathrm{CA}\)上に位置することが分かりました。 あとはこれらの内分比が等しいことを示せば良いですね。
そこで比を導き出すのに使うのが,チェバの定理です。 チェバの定理を使うと,次が成り立ちます。
また,条件③から次の式が成り立つのでした。
これらを見比べると,次の式が成り立つことが分かります。
したがって,点\(\mathrm{Q}\),\(\mathrm{Q}'\)は辺\(\mathrm{CA}\)を同じ比で内分するため,これらは同じ点です。 つまり\(\mathrm{BQ}\)と\(\mathrm{BQ}'\)は同じ直線であり,\(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)は,\(\mathrm{AP}\),\(\mathrm{BQ}'\),\(\mathrm{CR}\)と同じく共点です。
さて,後回しにした問題を解決しましょう。 \(\mathrm{AP}\)と\(\mathrm{CR}\)が平行である場合,どうなるのでしょうか?
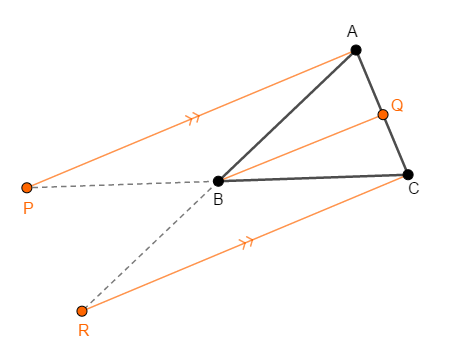
実は定理の条件①~③を満たす限り,このような場合はありえないのです。 つまり,何らかの矛盾が発生します。
まず錯角が等しいことから,\(\triangle\mathrm{BAP}\)と\(\triangle\mathrm{BRC}\)は相似です。
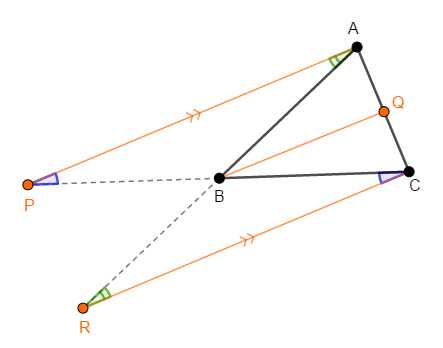
したがって,次の式が成り立ちます。
また,これを使って条件③の式を変形すると,次が成り立ちます。
最後の行では,再び\(\triangle\mathrm{BAP}\)と\(\triangle\mathrm{BRC}\)の相似を利用しています。
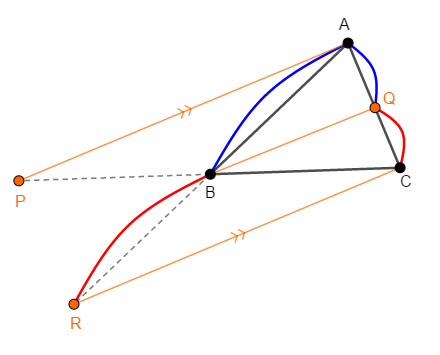
これで平行線と線分の比から,\(\mathrm{BQ}\)と\(\mathrm{CR}\)が平行であり,\(\mathrm{AP}\)も含めた\(3\)直線が全て平行であることが分かりました。 これは条件②に矛盾しますから,\(\mathrm{AP}\)と\(\mathrm{CR}\)は必ず交わるのです。
メネラウスの定理
次はメネラウスの定理を学びます。 チェバの定理は共点に関する定理でしたが,メネラウスの定理は共線に関する定理です。
\(\triangle\mathrm{ABC}\)とその頂点を通らない直線\(\ell\)を考える。 また,\(\ell\)は三角形の各辺またはその延長線と交わるとする。
このとき,各辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)(とその延長)が\(\ell\)と交わる点をそれぞれ\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)とすると,次が成り立つ。
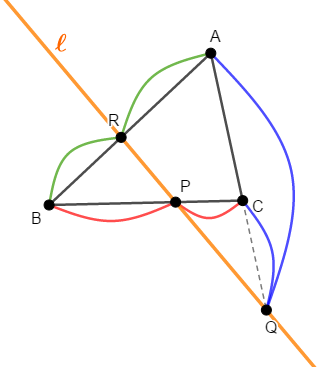
式の感じはチェバの定理と同じですね。 直線\(\ell\)が三角形の辺と交点を持たない場合でも,これは成り立ちます。
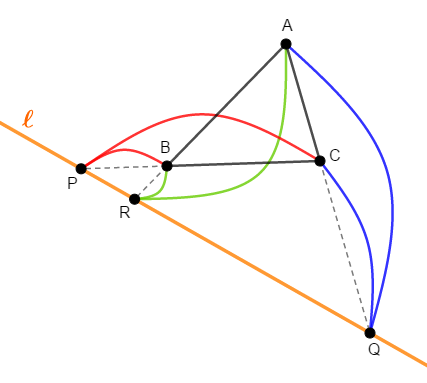
セットで登場することが多いチェバとメネラウスですが,実は生きた年代は全く違います。 メネラウスは\(1\)~\(2\)世紀,チェバは\(17\)~\(18\)世紀の人物です。
メネラウスの方が遥か過去の人物ですし,チェバの定理はメネラウスの定理から簡単に証明できます(確認問題に掲載)から,本当はメネラウスの定理から学ぶべきかもしれませんね。
それではメネラウスの定理を証明しましょう。 チェバの定理のときは,線分の比を面積比から考えましたが,今回は三角形がそれほど分割された感じがないので,別の方針でいきます。
比の積を約分できる形にすれば,その値が\(1\)になることを証明できるかもしれません。 約分できるように,なるべく比に統一感を持たせるため,平行線や三角形の相似を使って比を書き換えます。
まず平行線を使った比の変換を考えましょう。 \(\ell\)と平行で頂点\(\mathrm{C}\)を通る直線を考え,その対辺との交点を\(\mathrm{X}\)とします。
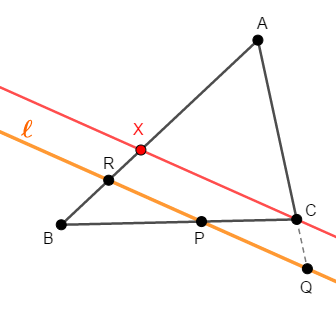
\(\triangle\mathrm{AXC}\)と\(\triangle\mathrm{ARQ}\)に注目すると,平行線と線分の比(または三角形の相似)から,次の比の式が得られます。
\(\triangle\mathrm{BRP}\)と\(\triangle\mathrm{BXC}\)に注目すると,平行線と線分の比(または三角形の相似)から,次の比の式が得られます。
したがって,証明したい比の式が次のように計算できます。
これでメネラウスの定理を証明できました。 次図のように\(\ell\)が三角形の外側にある場合でも,証明は全く変わりません。
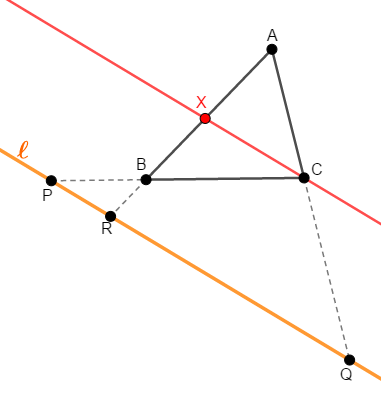
メネラウスの定理の逆も重要です。 次項で確認しましょう。
メネラウスの定理の逆
メネラウスの定理の逆は,次の内容です。 点たちが共線であることを証明するために使えます。
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)とその延長上にそれぞれ頂点でない点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)があるとする。 これが次の【条件】を全て満たすとき,\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)は共線である。(同一直線上にある。)
【条件】
① \(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)のうち,\(\triangle\mathrm{ABC}\)の辺上にあるのは,\(0\)点または\(2\)点である。
② 次の式が成り立つ。
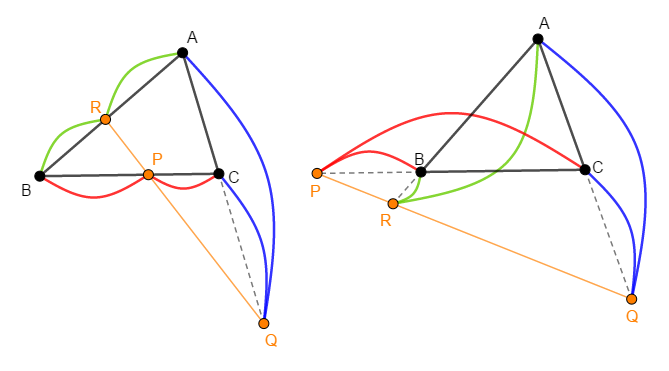
チェバの定理の逆と比べれば,複雑すぎるということはないですね。 とはいえ,学校で習う他の定理と比べると,ややこしい感じがしますし,特に条件①はピンときづらいですね。
そこで,少なくとも次の図の形は頭の中に入れておきましょう。 メネラウスの定理もその逆も,次の図のような状況に関する定理です。 それを文字に起こすからややこしいのであって,図の状況自体はそこまで複雑ではありません。
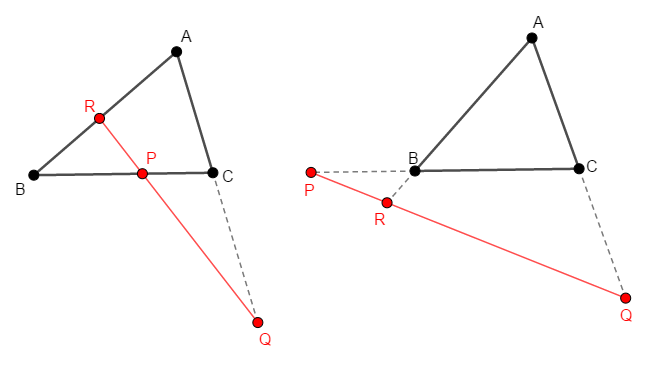
図を見れば,条件①の通り,辺上の点は\(0\)個(図右)か\(2\)個(図左)じゃないとダメだと分かります。
それでは,メネラウスの定理の逆を証明していきましょう。 条件①,②が成り立つことを前提に,\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が共線であることを示せばよいですね。
チェバの定理の逆を証明したときのように,この証明にはメネラウスの定理を活用できます。
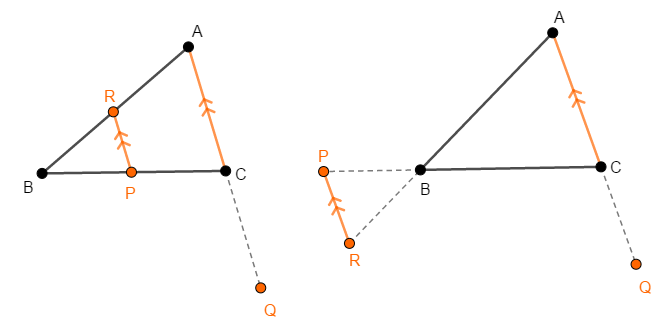
まず条件①から,点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)のうち,少なくとも\(1\)点は辺の延長上にあります。 ここでは点\(\mathrm{Q}\)が辺\(\mathrm{CA}\)の\(\mathrm{C}\)側の延長上にあるとしましょう。 次図のいずれかの状況ですね。
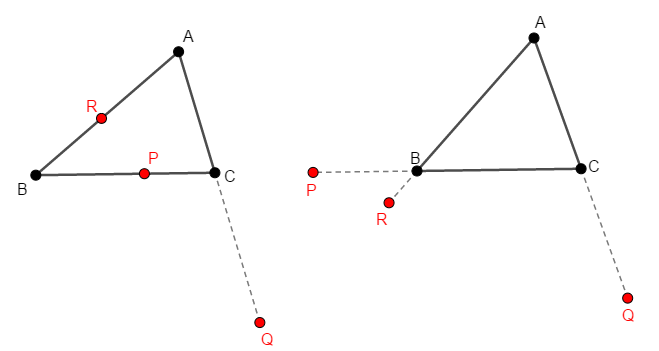
次に\(\mathrm{PR}\)と\(\mathrm{CA}\)の交点を\(\mathrm{Q}'\)とします。 あとは\(\mathrm{Q}\)と\(\mathrm{Q}'\)が一致することを示せば,証明完了です。
ここでチェバの定理と同様の疑問が浮かびます。 \(\mathrm{PR}\)と\(\mathrm{CA}\)に交点がない,つまり平行である場合を考慮しなければなりません。 このことについては,一度証明の流れを最後まで見てから補足します。
さて,\(\mathrm{Q}\)と\(\mathrm{Q}'\)が一致することを示したいのですが,まずは点\(\mathrm{Q}'\)が,\(\mathrm{Q}\)と同じく辺\(\mathrm{CA}\)の延長上にある(つまり外分点である)ことを確認しましょう。
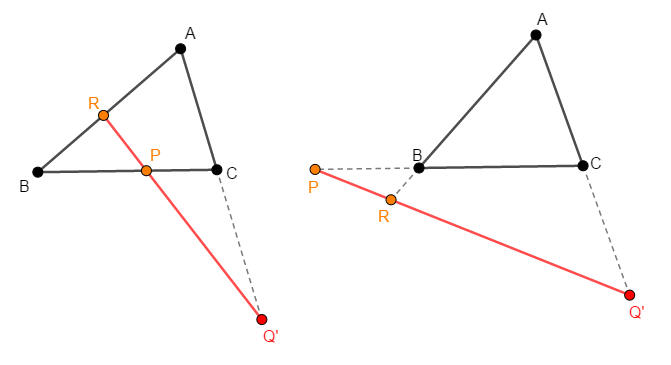
図左の場合も図右の場合も,もし直線\(\mathrm{PR}\)が辺\(\mathrm{CA}\)上で交わるとすれば,この直線は三角形と奇数回交わったことになります。 ところが直線が三角形を横切る回数は,偶数回しかありえません。
直線上の点を順に追っていくと,初めは三角形の外部にありますが,\(1\)回三角形と交わった時点で内部に入ります。 直線は最終的に三角形の外部に出るために,もう\(1\)回三角形と交わる必要があります。
つまり,直線が三角形の辺と交わる回数は\(0\)回か\(2\)回,すなわち偶数回です。 したがって,直線\(\mathrm{PR}\)が辺\(\mathrm{CA}\)上で交わることはありえません。
これで点\(\mathrm{Q}'\)が辺\(\mathrm{CA}\)の延長上に位置することが分かりました。 それが\(\mathrm{C}\)側か\(\mathrm{A}\)側かはまだはっきりしませんが,\(\mathrm{Q}\)と\(\mathrm{Q}'\)が辺\(\mathrm{CA}\)を外分する比が同じであると示せば,両者が一致することを示せます。
そこで比を導き出すのに使うのが,メネラウスの定理です。 メネラウスの定理を使うと,次が成り立ちます。
また,条件②から次の式が成り立つのでした。
これらを見比べると,次の式が成り立つことが分かります。
したがって,点\(\mathrm{Q}\),\(\mathrm{Q}'\)は辺\(\mathrm{CA}\)を同じ比で外分するため,これらは同じ点です。 つまり\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)は,\(\mathrm{P}\),\(\mathrm{Q}'\),\(\mathrm{R}\)と同じく共線です。
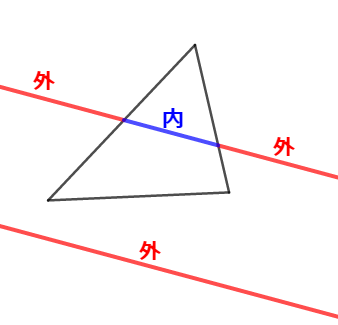
さて,後回しにした問題を解決しましょう。 \(\mathrm{PR}\)と\(\mathrm{CA}\)が平行である場合,どうなるのでしょうか?
まず条件①より,点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)のうち,少なくとも\(1\)点は辺の外分点であることを確認しておきます。 ここでは点\(\mathrm{Q}\)が辺\(\mathrm{CA}\)の外分点であるとしましょう。
平行線と線分の比(または三角形の相似)より,図左・図右いずれの場合でも,次が成り立ちます。
これを使って条件②の式を変形すると,次が成り立ちます。
したがって,\(\mathrm{CQ} : \mathrm{QA} = 1 : 1\)になりますが,この比は\(\mathrm{Q}\)が辺\(\mathrm{CA}\)の外分点であることに矛盾しますから,\(\mathrm{PR}\)と\(\mathrm{CA}\)は必ず交わるのです。
確認問題
メネラウスの定理を使って,チェバの定理を証明してください。
答え
まずは図をかきましょう。 \(\triangle\mathrm{ABC}\)とチェバの定理の条件に合う点\(\mathrm{X}\)をとります。 また,頂点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)と点\(\mathrm{X}\)を結ぶ直線が対辺と交わる点をそれぞれ\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)とします。
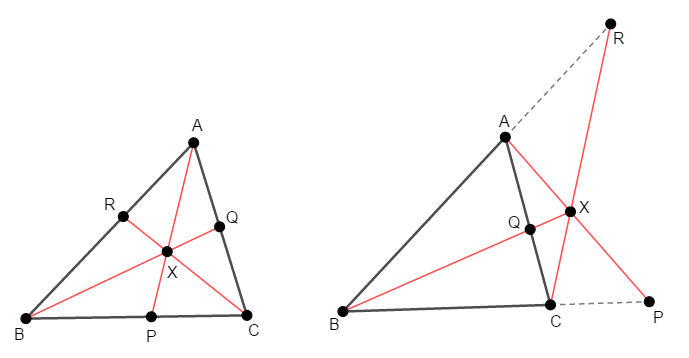
この図で次の式が成り立つことを証明すれば良いですね。
メネラウスの定理を使うためには,図の中から「三角形と直線の組み合わせ」を探す必要があります。 最終的に上の式を導くことを意識しながら,メネラウスの定理を使います。
まずは好きな三角形と直線に注目します。 例えば次図のように\(\triangle\mathrm{ABP}\)と直線\(\mathrm{CR}\)に注目します。
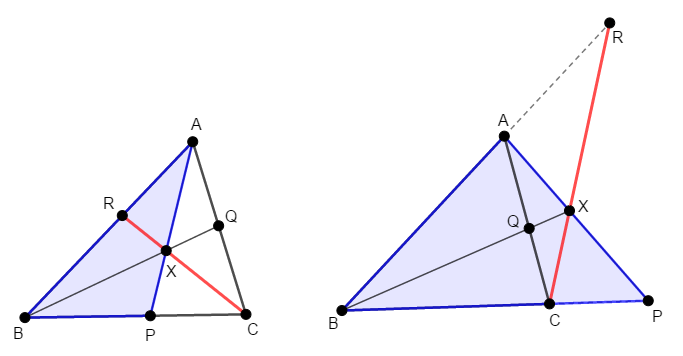
この図にメネラウスの定理を適用すると,図左・図右いずれの場合でも,次の式が成り立ちます。
とりあえず適当な図でメネラウスの定理を使いましたが,最終的に導きたい式とは無関係の\(\mathrm{PX}\)や\(\mathrm{XA}\)が出てきてしまいました。
この要らない部分を打ち消すため,\(\mathrm{PX}\)や\(\mathrm{XA}\)が登場する別の「三角形と直線の組み合わせ」を探すと,次図のように\(\triangle\mathrm{ACP}\)と直線\(\mathrm{BQ}\)が見つかります。
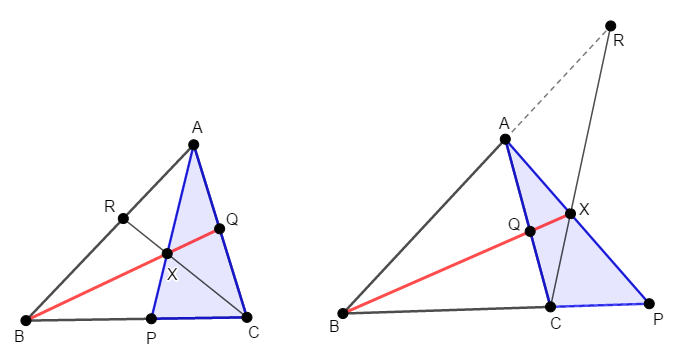
この図にメネラウスの定理を適用すると,図左・図右いずれの場合でも,次の式が成り立ちます。
これら\(2\)つの式の\(\displaystyle\frac{\mathrm{PX}}{\mathrm{XA}}\)が共通することに注目すると,次の式が成り立ちます。
この式を整理することで,次のチェバの定理の式が得られます。 これでチェバの定理が証明されました。
次の図について,\(x\),\(y\)を求めてください。
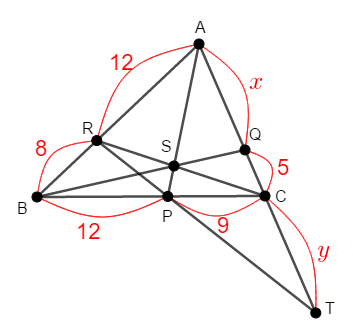
答え
\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)は\(\triangle\mathrm{ABC}\)の辺上の点で,\(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)が共点なので,\(\triangle\mathrm{ABC}\)でチェバの定理を使えます。
また,上記に加えて辺\(\mathrm{CA}\)の延長上に\(\mathrm{T}\)があり,\(\mathrm{R}\),\(\mathrm{P}\),\(\mathrm{T}\)が共線なので,\(\triangle\mathrm{ABC}\)と直線\(\mathrm{RT}\)でメネラウスの定理を使えます。
チェバの定理の逆を使って,三角形の内角の二等分線\(3\)本が共点であることを証明してください。
答え
チェバの定理の逆を使って共点を示すには,\(3\)つの条件を確認する必要がありました。 よく確認しておきましょう。
\(\triangle\mathrm{ABC}\)の\(\angle\mathrm{A}\),\(\angle\mathrm{B}\),\(\angle\mathrm{C}\)の二等分線がその対辺(またはその延長線)と交わる点をそれぞれ\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)とします。 また,\(\mathrm{BC} = a\),\(\mathrm{CA} = b\),\(\mathrm{AB} = c\)とします。
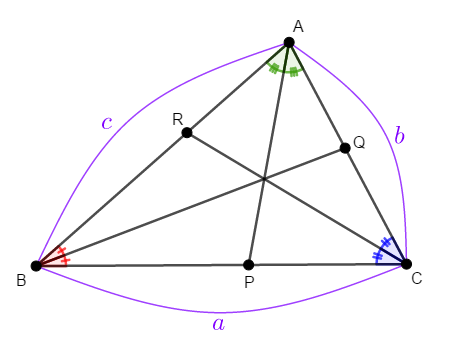
まず\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が全て辺上の点であることを確認します。 内角の二等分線上の点は,当然その内角の内部にあります。 また,その内角の対辺も内角の内部にありますから,内角の二等分線と対辺を含む直線の交点は,必ず対辺上にあります。
次に各内角の二等分線が,すべて互いに交わることを確認します。 例えば\(\angle\mathrm{A}\)の二等分線\(\mathrm{AP}\)と\(\angle\mathrm{B}\)の二等分線\(\mathrm{BQ}\)を考えます。 \(\mathrm{AP}\)によって二等分された角のうち,\(\angle\mathrm{BAP}\)側に点\(\mathrm{B}\),\(\angle\mathrm{CAP}\)側に点\(\mathrm{Q}\)があるので,これらを結ぶ直線\(\mathrm{BQ}\)は\(\mathrm{AP}\)と交わります。
最後にチェバの定理の逆の式が成り立つことを確認します。 三角形の内角の二等分線とその対辺の交点は,対辺をその内角の両側の辺の長さの比で内分するので,次の式が成り立ちます。
この式から,次が成り立つことが分かります。
以上から,三角形の内角の二等分線はすべて対辺と辺上で交わり,それら二等分線は互いに交わり,上の式が成り立つため,チェバの定理の逆より,これら二等分線は共点です。
次の図で,\(\triangle\mathrm{ABC}\)と\(\triangle\mathrm{A}'\mathrm{B}'\mathrm{C}'\)は,\(\mathrm{AA}'\),\(\mathrm{BB}'\),\(\mathrm{CC}'\)が共点(共有点は\(\mathrm{O}\))であるような三角形です。
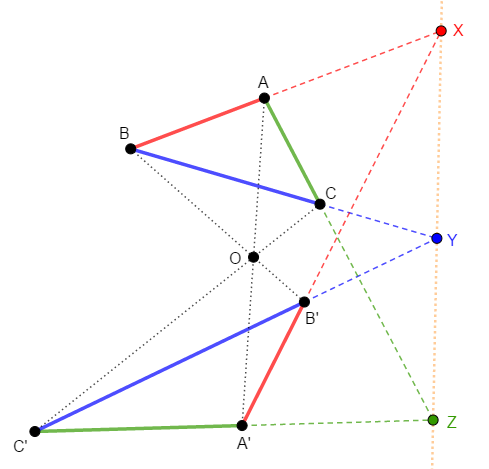
このとき,直線\(\mathrm{AB}\)と\(\mathrm{A}'\mathrm{B}'\),\(\mathrm{BC}\)と\(\mathrm{B}'\mathrm{C}'\),\(\mathrm{CA}\)と\(\mathrm{C}'\mathrm{A}'\)それぞれの交点を\(\mathrm{X}\),\(\mathrm{Y}\),\(\mathrm{Z}\)とすると,これらが共線であることを証明してください。
答え
メネラウスの定理の逆を使って共線を示すには,\(2\)つの条件を確認する必要がありました。 よく確認しておきましょう。
\(\triangle\mathrm{ABC}\)と点\(\mathrm{X}\),\(\mathrm{Y}\),\(\mathrm{Z}\)に対してメネラウスの定理の逆を適用することを考えます。 図から\(3\)点とも\(\triangle\mathrm{ABC}\)の辺の延長上にあることが分かります。
あとは次の式が成り立つことを証明できれば,メネラウスの定理の逆を適用できます。
この式を得るために,式のパーツを\(1\)つずつ得ることにします。 まず\(\displaystyle\frac{\mathrm{AX}}{\mathrm{XB}}\)を得ることを考えると,\(\triangle\mathrm{OAB}\)と直線\(\mathrm{A}'\mathrm{B}'\)に対してメネラウスの定理を使えば良いですね。
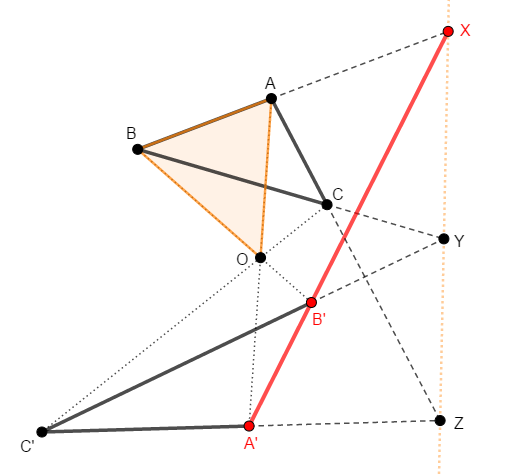
なぜこの三角形と直線に注目するかというと,この比を登場させるには,辺\(\mathrm{AB}\)をもつ三角形と点\(\mathrm{X}\)を通る直線が必要だからです。 そう考えると,\(\mathrm{X}\)を通る直線として考えられるのは\(\mathrm{A}'\mathrm{B}'\)ですし,この直線上の点\(\mathrm{A}'\),\(\mathrm{B}'\)が辺の延長上にある三角形として考えられるのは\(\triangle\mathrm{OAB}\)です。
この三角形と直線に対してメネラウスの定理を使うと,次の式が得られます。
同様に,次は\(\displaystyle\frac{\mathrm{BY}}{\mathrm{YC}}\)を得るために\(\triangle\mathrm{OBC}\)と直線\(\mathrm{B}'\mathrm{C}'\)を考えます。
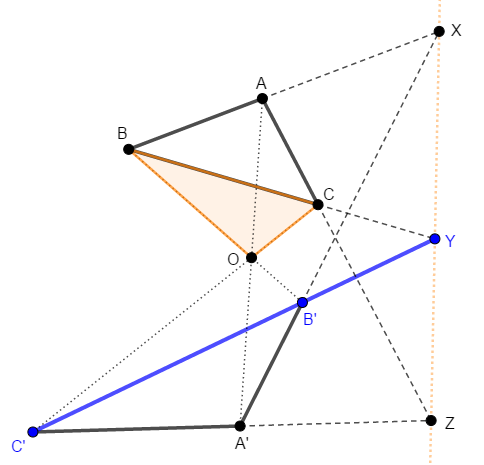
この三角形と直線に対してメネラウスの定理を使うと,次の式が得られます。
残りの\(\displaystyle\frac{\mathrm{CZ}}{\mathrm{ZA}}\)を得るために\(\triangle\mathrm{OCA}\)と直線\(\mathrm{C}'\mathrm{A}'\)を考えます。
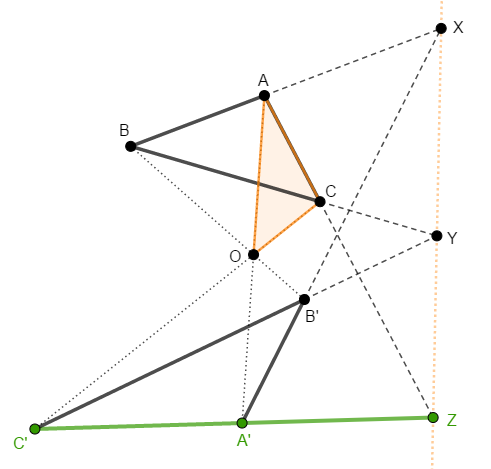
この三角形と直線に対してメネラウスの定理を使うと,次の式が得られます。
得られた\(3\)つの式を辺々掛けると,次の目的の式が得られます。
以上から,メネラウスの定理の逆により,\(3\)点\(\mathrm{X}\),\(\mathrm{Y}\),\(\mathrm{Z}\)が共線であることが示されました。
これを一般化した定理がデザルグの定理です。
