これまで内分・外分を学び,その延長として三角形の五心などを考えてきました。 今回はここで一度,三角形そのものの基本的な性質のうち,中学では習わなかったものを確認しておきましょう。
目次
辺と角の大小
三角形の辺同士や角同士の大小関係を意識すると,議論が簡単になる場合があります。 例えばある三角形が鋭角三角形であることを証明するには,最大角が鋭角であることを示せば十分です。
内角がすべて鋭角である三角形のことを鋭角三角形といいます。 最大角が鋭角なら,それより小さい他の内角も当然鋭角になりますね。
次の事実を知っておくと,三角形の辺同士や各同士の大小関係を知る有用な手掛かりになります。
三角形の内角の大小関係は,その対辺の大小関係と等しい。
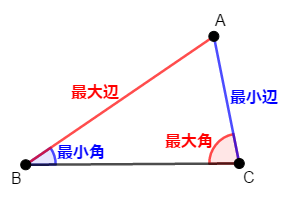
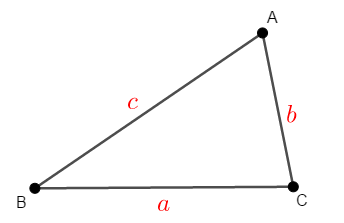
\(\triangle\mathrm{ABC}\)の内角\(\angle\mathrm{A}\),\(\angle\mathrm{B}\),\(\angle\mathrm{C}\)の対辺の長さをそれぞれ\(a\),\(b\),\(c\)とし,このことを証明してみましょう。
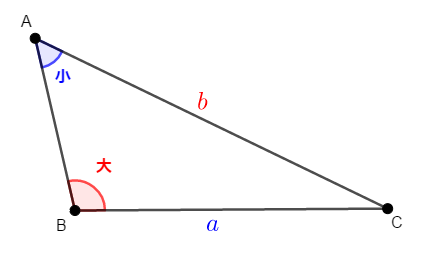
まず\(\angle\mathrm{A} < \angle\mathrm{B}\)のとき,\(a < b\)であることを証明します。 次の図のような状況です。
ここで比較したいのは\(a\)と\(b\),すなわち\(\mathrm{BC}\)と\(\mathrm{CA}\)です。 その比較のため,辺\(\mathrm{CA}\)(またはその\(\mathrm{A}\)側の延長)上に\(\mathrm{CB} = \mathrm{CP}\)となる点\(\mathrm{P}\)をとってみましょう。
もし本当に\(\mathrm{BC} < \mathrm{CA}\)なら,次図のように点\(\mathrm{P}\)は辺\(\mathrm{CA}\)上にあるはずです。
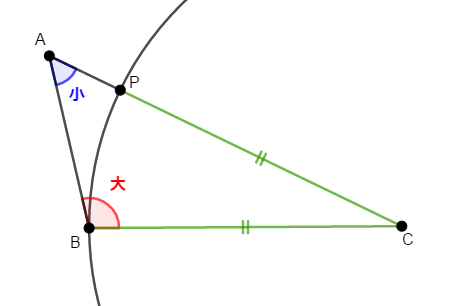
ということは,上図のようにならないと仮定すれば,必ず矛盾が生じるはずですから,そのことを確認してみましょう。 このような論法を背理法といいましたね。
まず,もし点\(\mathrm{P}\)が点\(\mathrm{C}\)と一致したらどうなるか考えます。
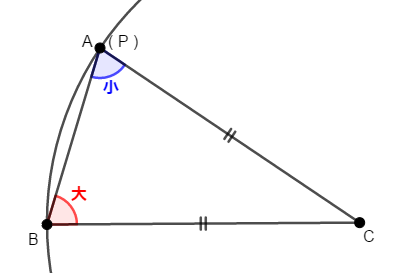
このとき,\(\triangle\mathrm{ABC}\)は\(\mathrm{BC} = \mathrm{CA}\)である二等辺三角形ですから,底角が等しいので\(\angle\mathrm{A} = \angle\mathrm{B}\)となってしまいます。 これは\(\angle\mathrm{A} < \angle\mathrm{B}\)に矛盾するのでありえません。
次にもし点\(\mathrm{P}\)が辺\(\mathrm{CA}\)の延長上にあるとどうなるか考えます。
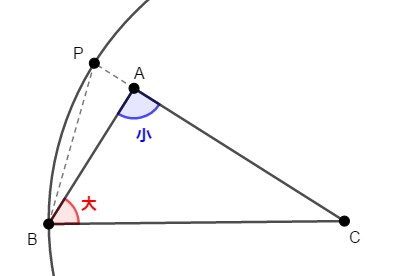
このとき,\(\triangle\mathrm{ABC}\)と\(\triangle\mathrm{PBC}\)に注目してみると,両者とも\(\angle\mathrm{C}\)が共通ですが,\(\angle\mathrm{ABC} < \angle\mathrm{PBC}\)です。 したがって,三角形の内角の和が一定(\(180^{\circ}\))であることから,\(\angle\mathrm{BAC} > \angle\mathrm{BPC}\)です。
このことから,次の不等式が成立します。
しかし,\(\triangle\mathrm{PBC}\)は\(\mathrm{BC} = \mathrm{PC}\)である二等辺三角形ですから,底角が等しいので\(\angle\mathrm{PBC} = \angle\mathrm{BPC}\)であるはずです。 これは上の不等式と矛盾しますから,この状況もありえません。
以上から,点\(\mathrm{P}\)は辺\(\mathrm{CA}\)上に位置するため,次の不等式が成立することが分かります。
次に\(a < b\)のとき,\(\angle\mathrm{A} < \angle\mathrm{B}\)であることを証明します。 次の図のような状況です。
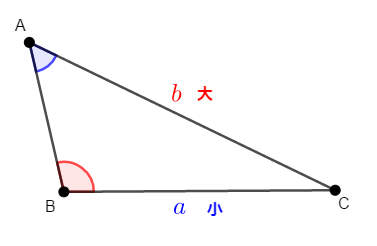
証明の発想は先ほどと同じようなものです。 \(b\)の方が大きい分だけ対角が大きいのなら,その余った長さに注目しましょう。
辺\(\mathrm{CA}\)上に\(\mathrm{CB} = \mathrm{CP}\)となる点\(\mathrm{P}\)をとります。
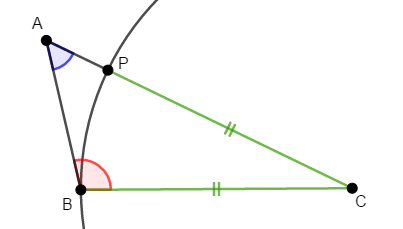
ここで\(\triangle\mathrm{PBC}\)は\(\mathrm{BC} = \mathrm{PC}\)である二等辺三角形ですから,底角が等しいので\(\angle\mathrm{PBC} = \angle\mathrm{BPC}\)です。 また,\(\triangle\mathrm{APB}\)で外角\(\angle\mathrm{BPC}\)に注目すると,\(\angle\mathrm{BPC} = \angle\mathrm{BAP} + \angle\mathrm{ABP}\)です。
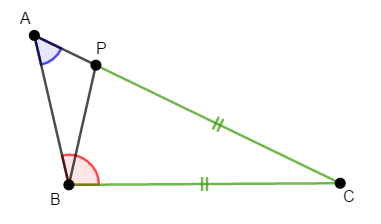
以上から,次の不等式が成り立ちます。
これで三角形の内角の大小関係が,その対辺の大小関係と等しいことが確認できましたね。
三角形の成立条件
三角形の内角はどんな値でもとれるわけではありません。 内角の和が\(180^{\circ}\)にならないといけないですね。
同様に三角形の辺も,どんな値でもとれるわけではありません。 次の不等式を満たさなくてはなりません。
三角形の\(3\)辺の長さ\(a\),\(b\),\(c\)は,次の不等式(三角不等式)を満たさなければならない。
逆に,\(a\),\(b\),\(c\)が上の不等式を満たすとき,これらを\(3\)辺の長さとする三角形が存在する。
つまり三角形の辺は,他の\(2\)辺の差よりも大きく,和よりも小さくなければならないのです。
まずはどうしてこの不等式が必要か,具体例を見て理解しましょう。 \(a = 2\),\(b = 3\),\(c = 6\)はこの不等式を満たしませんが,なぜこのとき三角形が作れないのでしょう?
長さ\(2\),\(3\),\(6\)の線分を組み合わせて三角形を作ろうとしてみれば,すぐ分かります。 最長の線分の両端に他\(2\)つの線分を取り付けてみましょう。
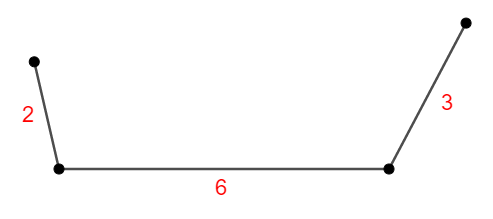
あとは両端の線分を内側に折りたためば,三角形が作れるはずです・・・が! 両側の線分は決して交わらず,三角形を作ることができないのです。
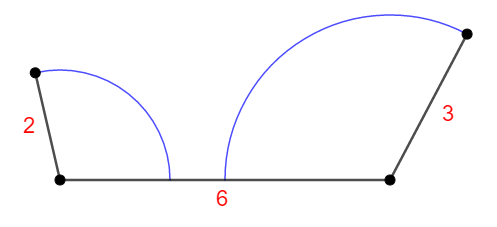
これは\(2\)と\(3\)を足しても\(6\)に届かないからです。 三角形の成立条件は,こうならないために必要なのです。
\(|a - b| < c\)はピンと来ないかもしれませんが,絶対値を外してみれば分かる通り,これは\(a < b + c\)と\(b < c + a\)を集約した不等式です。 つまり三角形の成立条件は,次のようにも言い換えられます。
\(3\)辺の長さが\(a\),\(b\),\(c\)である三角形が存在するための必要十分条件は,次の不等式(三角不等式)である。
では\(\triangle\mathrm{ABC}\)の内角\(\angle\mathrm{A}\),\(\angle\mathrm{B}\),\(\angle\mathrm{C}\)の対辺の長さをそれぞれ\(a\),\(b\),\(c\)とし,上の不等式を証明してみましょう。
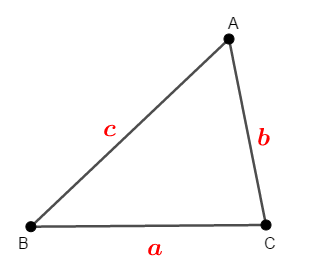
まず\(c < a + b\)を証明します。 \(a + b\)を考えやすくするために,次図のように辺\(\mathrm{BC}\)の延長上に\(\mathrm{CP} = b\)である点\(\mathrm{P}\)をとります。
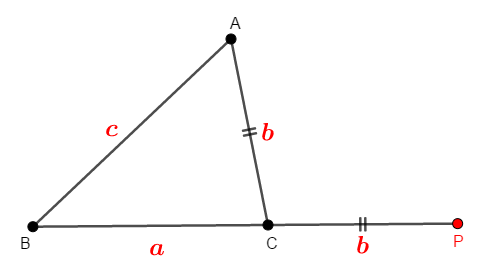
こうすれば\(\mathrm{BP} = a + b\)ですから,\(a + b\)を考えやすいですね。 さらに\(\mathrm{AB} = c\)ですから,\(a + b\)と\(c\)はともに\(\triangle\mathrm{ABP}\)の辺の長さです。
これで不等式が,三角形の辺の長さの大小関係を表すようになりました。 前項で学んだ通り,辺の大小関係はその対角の大小関係と等しいので,次は\(\triangle\mathrm{ABP}\)の内角に注目しましょう。
まず\(\triangle\mathrm{ACP}\)が二等辺三角形であることから,底角が等しいので\(\angle\mathrm{CAP} = \angle\mathrm{CPA}\)であることが分かります。
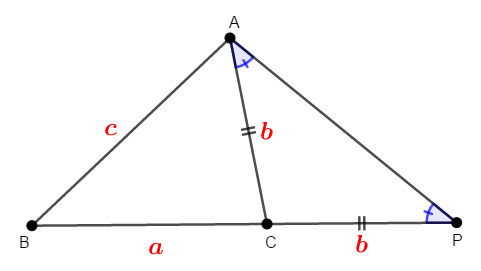
したがって,次の不等式が成り立ちます。
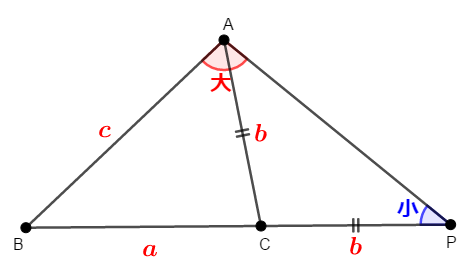
これは\(\triangle\mathrm{ABP}\)の内角の大小関係ですが,これはそのまま対辺の大小関係についても成り立ちますから,\(c < a + b\)であることが示されました。
次は\(|a - b| < c\)を証明するのですが,まず上の議論と全く同様にして,次の\(2\)つの不等式も成り立ちます。
この\(2\)つの不等式を少し変形すると,次のようになります。
これで\(|a - b| < c\)が証明できました。 あっという間でしたね。
\(|a - b|\)の絶対値を外すと,\(a - b\)か\(b - a\)になります。 \(c\)はそのどちらよりも大きいのですから,上の不等式が成り立ちます。
全く同様にして,\(|b - c| < a\),\(|c - a| < b\)も成り立ちます。
最後に逆についても考えましょう。 ここまでで証明したのは,三角形が成立するための必要条件だけです。 これが十分条件になれるかは,未確認です。
証明しなければならないのは,次の不等式を満たす\(a\),\(b\),\(c\)を\(3\)辺の長さとする三角形が存在することです。
三角形が存在することを証明する手っ取り早い方法は,実際に三角形を作ってしまうことです。 長さ\(c\)の線分\(\mathrm{AB}\)の両端に長さ\(a\),\(b\)の線分を取り付けます。
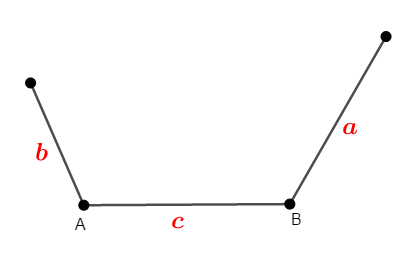
点\(\mathrm{A}\)を中心とする半径\(b\)の円,点\(\mathrm{B}\)を中心とする半径\(a\)の円をかくと,条件の不等式より,これらは交点を持ちますから,その\(1\)つを\(\mathrm{C}\)とします。

ここで\(\mathrm{AC} = b\),\(\mathrm{BC} = a\)ですから,\(a\),\(b\),\(c\)を\(3\)辺の長さとする\(\triangle\mathrm{ABC}\)が存在することが分かりました。
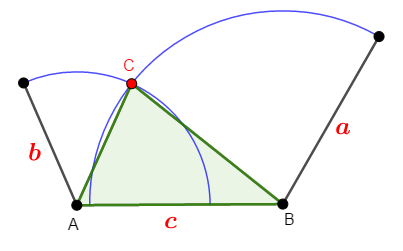
さて,明らかに\(1\)箇所,説明不足な点がありました。 途中で\(2\)つの円の交点が存在するといいましたが,これは明らかではありません。 もう少し説明が必要です。
まず\(c < a + b\)が成り立っているおかげで,\(2\)つの円が届かないという事態が避けられます。
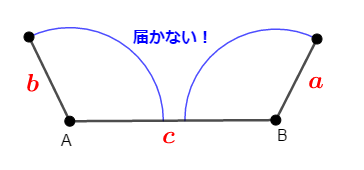
ただこれだけでは十分ではありません。 例えば\(a > b\)の場合,もし\(a > b + c\),すなわち\(a - b > c\)になってしまうと,\(2\)つの円は交点を持ちません。
(下図でオレンジの線の長さが\(b + c\)です。)
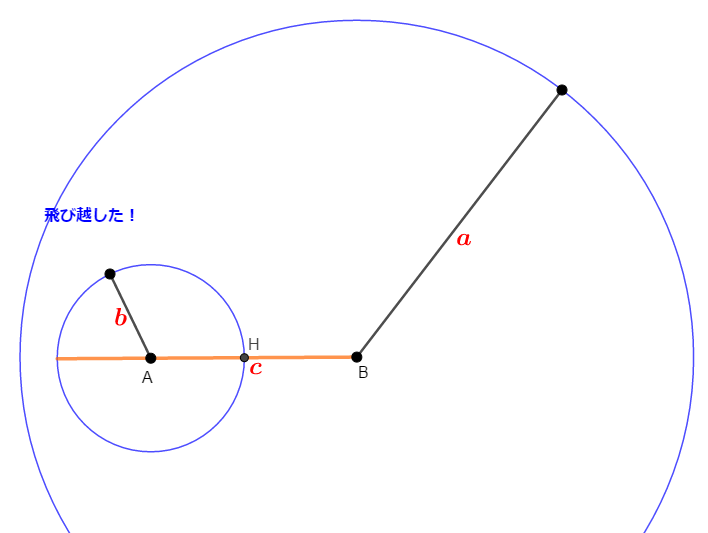
\(a - b = c\)の場合,交点はありますが,その交点は辺\(\mathrm{AB}\)の延長上にできてしまうので,三角形を作れません。 同様に,\(a < b\)の場合も\(b - a \geqq c\)になってはいけません。
そこで\(|a - b| < c\)という条件が効いてきます。 この条件のおかげで,\(2\)つの円に交点があり,三角形を作れるようになるのです。
確認問題
次図で\(\mathrm{AB} > \mathrm{AC}\)であるとき,\(\mathrm{AB} > \mathrm{AP}\)であることを証明してください。
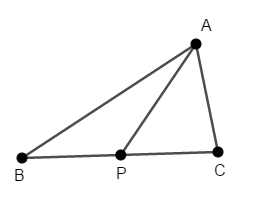
答え
\(\mathrm{AB} > \mathrm{AC}\)なので,\(\angle\mathrm{C} > \angle\mathrm{B}\)です。
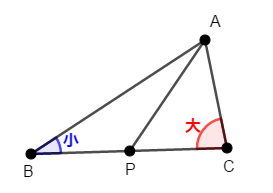
証明したいのは\(\mathrm{AB} > \mathrm{AP}\)ですから,\(\triangle\mathrm{ABP}\)に注目します。 この三角形において,\(\angle\mathrm{P} > \angle\mathrm{B}\)を証明できれば良いですね。
ここで,\(\angle\mathrm{P}\)すなわち\(\angle\mathrm{APB}\)は,\(\triangle\mathrm{APC}\)の外角ですから,次が成り立ちます。
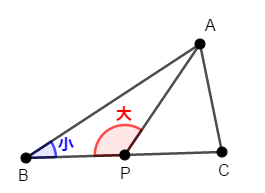
したがって,\(\triangle\mathrm{ABP}\)において\(\angle\mathrm{P} > \angle\mathrm{B}\)ですから,\(\mathrm{AB} > \mathrm{AP}\)です。
\(3\)辺の長さを\(x\),\(2x + 1\),\(7\)とする三角形が存在する\(x\)の範囲を求めてください。
答え
\(3\)辺の長さを三角形の成立条件に当てはめ,不等式を解きましょう。
ここで\(x\)が辺の長さであるためには,当然\(x > 0\)である必要がありますから,\(x + 1 > 0\)です。 したがって,\(|x + 1| = x + 1\)です。
このように不等号の連続する不等式は,前半・後半の不等式に分けて連立させて解きます。
これを解くと\(2 < x < 6\)です。 これが求める\(x\)の範囲です。
\(a\),\(b\),\(c\)のうち最大の数を\(a\)とします。 このとき,これらを\(3\)辺の長さとする三角形が存在するための十分条件が,次の不等式だけで良いことを証明してください。
答え
\(a < b + c\)が成り立つとき,本文で学んだ三角形の成立条件が成り立つことを証明します。 つまり,\(|b - c| < a\)か,\(b < c + a\)かつ\(c < a + b\)が成り立つことを証明すれば良いです。
最大辺が\(a\)なのですから,\(b < a\)かつ\(c < a\)です。 したがって,当然\(b < c + a\)と\(c < a + b\)も成り立ち,三角形の成立条件が満たされます。
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\)の中点を\(\mathrm{M}\)とします。 このとき,\(2\mathrm{AM} < \mathrm{AB} + \mathrm{AC}\)が成り立つことを証明してください。
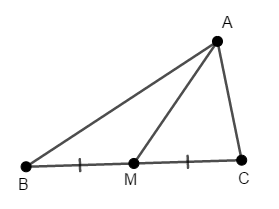
答え
左辺の\(2\mathrm{AM}\)を見れば思い付くと思いますが,線分\(\mathrm{AM}\)を長さ\(2\)倍で延長しましょう。 つまり\(\mathrm{M}\)側の延長上に\(\mathrm{AM} = \mathrm{MP}\)である点\(\mathrm{P}\)をとります。
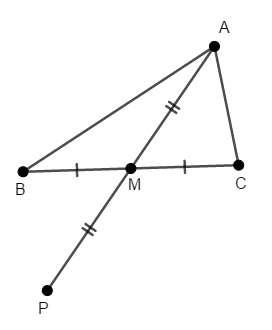
ここで四角形\(\mathrm{ABPC}\)に注目すると,対角線がそれぞれの中点で交わっていますから,これは平行四辺形です。 よって,その対辺は等しいですから,\(\mathrm{BP} = \mathrm{AC}\)です。
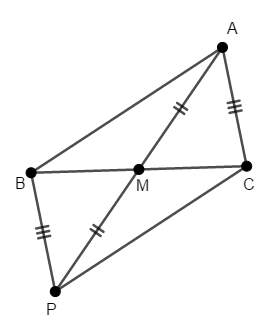
したがって,\(\triangle\mathrm{ABP}\)に注目すると,次の不等式が成り立つことが分かります。
証明中で見たように,中線を長さ\(2\)倍で延長すると,平行四辺形ができあがります。 何かと使う場面がありますから,頭の片隅に入れておきましょう。
