今回は軽めの内容です。 前回学んだ三角形の成立条件の式から,\(2\)点間の最短経路を考えましょう。
目次
最短経路
\(2\)点を結ぶ最短経路はどんなものでしょうか? 直感では,それらを結ぶ線分がそうですね。

直感だけでは不安ですから,このことを少し確認しましょう。 例えば,点\(\mathrm{A}\)から点\(\mathrm{B}\)へ向かうのに,次のように点\(\mathrm{P}\)を経由してみます。
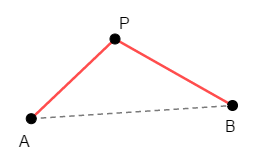
このとき,\(\triangle\mathrm{ABP}\)に注目すると,三角不等式から次が成り立ちます。
この不等式からも,\(\mathrm{P}\)を経由せずに直接\(\mathrm{A}\)と\(\mathrm{B}\)を結ぶ線分の方が短い経路ですね。
次のように曲線経路を考えた場合はどうでしょうか?
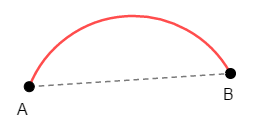
曲線に三角不等式は使えませんが,曲線を次のような折れ線をどこまでも細かくしたものと考えれば,やはり寄り道せずに直接繋ぐ線分が最短経路だと分かります。
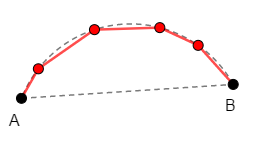
というわけで,次が確認できました。
\(2\)点間の最短経路は,それらを結ぶ線分である。
確認問題
四角形\(\mathrm{APQB}\)に対して,次の不等式が成り立つことを証明してください。
答え
線分\(\mathrm{PB}\)を引き,まず\(\triangle\mathrm{APB}\)に注目します。 三角不等式より,次の不等式が成り立ちます。
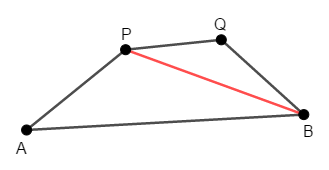
さらに\(\triangle\mathrm{PQB}\)に注目すると,三角不等式より次が成り立ちます。
以上の\(2\)つの不等式から,次の不等式が成り立つことが分かります。
直線状の川と\(2\)地点\(\mathrm{A}\),\(\mathrm{B}\)があります。 川と岸の境界を直線\(\ell\)と呼ぶことにします。
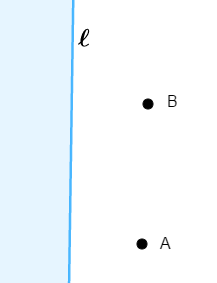
今,地点\(\mathrm{A}\)にいる人は,\(\ell\)上の\(1\)点で水を汲んでから地点\(\mathrm{B}\)に向かう必要があるとします。 これを最短経路で行うためには,\(\ell\)上のどんな点で水を汲めば良いでしょうか?
答え
\(\ell\)上に\(\mathrm{AP} + \mathrm{PB}\)が最小となるような点\(\mathrm{P}\)をとるならどこか? という問題ですね。
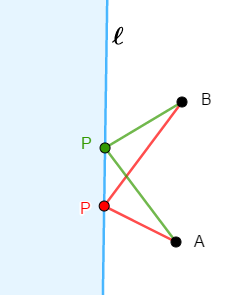
しかし,これは折れ線の長さを比べることになり,考えづらいです。 なぜ折れ線になってしまうのかというと,\(\mathrm{A}\),\(\mathrm{B}\)が\(\ell\)に関して同じ側にあるからです。
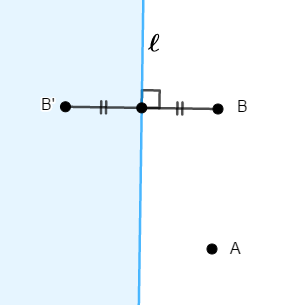
これを考えやすくするため,\(\mathrm{B}\)の代わりの点\(\mathrm{B}'\)を,\(\ell\)に関して\(\mathrm{A}\)の反対側にとることを考えましょう。
川から地点\(\mathrm{B}\)に行く距離を考える代わりに,地点\(\mathrm{B}'\)に行く距離を考えるわけですから,\(\mathrm{B}'\)と\(\ell\)の距離は,\(\mathrm{B}\)と\(\ell\)の距離と等しい必要があります。 つまり,点\(\mathrm{B}'\)は\(\ell\)に関する\(\mathrm{B}\)の対称点であれば良いです。
これで\(\mathrm{AP} + \mathrm{PB}'\)を最小化する\(\mathrm{P}\)を考えれば良くなりましたが,\(\mathrm{A}\)から\(\mathrm{B}'\)に向かう際,寄り道せず一直線で向かうのが最短経路です。 したがって,点\(\mathrm{P}\)は線分\(\mathrm{AB}'\)と\(\ell\)の交点としてとるべきです。
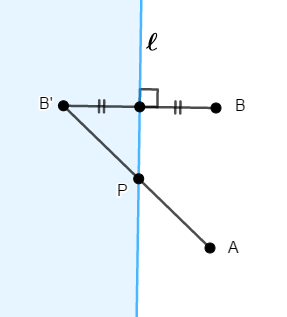
このとき,確かに\(\mathrm{PB} = \mathrm{PB}'\)であり,\(\mathrm{AP} + \mathrm{PB} = \mathrm{AP} + \mathrm{PB}'\)ですね。
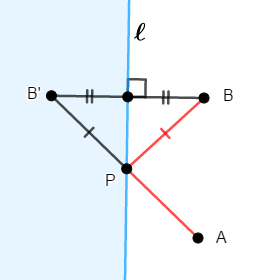
以上から,答えは「\(\ell\)に関して\(\mathrm{B}\)と対称な点\(\mathrm{B}'\)をとり,\(\ell\)と線分\(\mathrm{AB}'\)の交点で水を汲めば良い」です。
