ここからは円に関わる平面図形を学んでいきます。 まずは円に内接する四角形を見ていきましょう。
目次
円に内接する四角形の性質
三角形の外接円・内接円やタレスの定理など,これまでに円と三角形の関わりを色々見てきました。 次に考えるのは,円と四角形の関わりです。
ここでは円に内接する四角形を考えます。 (外接については今回学びませんが,次回学ぶ接線の知識などが役立つでしょう。)
円に内接する四角形について,次が成り立ちます。
円に内接する四角形について,次が成り立つ。
- 対角の和は\(180^{\circ}\)である。
- 内角とその対角の外角は等しい。
では証明しましょう。 円\(\mathrm{O}\)に内接する四角形\(\mathrm{ABCD}\)を考え,\(\angle\mathrm{A} + \angle\mathrm{C} = 180^{\circ}\)を証明します。
\(\angle\mathrm{A} = \alpha\),\(\angle\mathrm{C} = \beta\)とします。 \(\angle\mathrm{A}\)も\(\angle\mathrm{C}\)もこの円の円周角ですから,中心角と結び付けて考えましょう。 そのために線分\(\mathrm{OB}\),\(\mathrm{OD}\)を引きます。
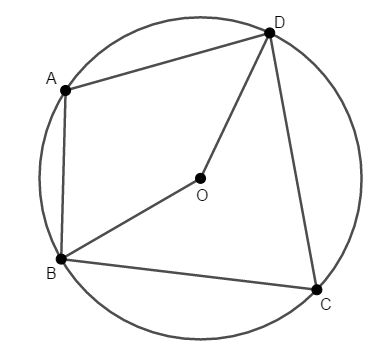
\(\angle\mathrm{A} = \alpha\)は弧\(\mathrm{BCD}\)に対する円周角ですから,円周角の定理より,同じ弧に対する中心角は\(2\alpha\)です。 同様に弧\(\mathrm{BAD}\)に対する中心角は\(2\beta\)です。
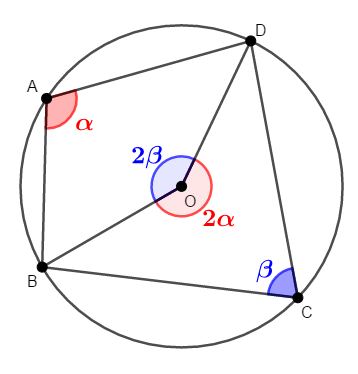
ここで,\(2\alpha + 2\beta = 360^{\circ}\)ですから,\(\alpha + \beta = 180^{\circ}\)が成り立ちます。 つまり対角の和が\(180^{\circ}\)であることが分かりました。
ということは当然,内角とその対角の外角が等しいということもいえますね。
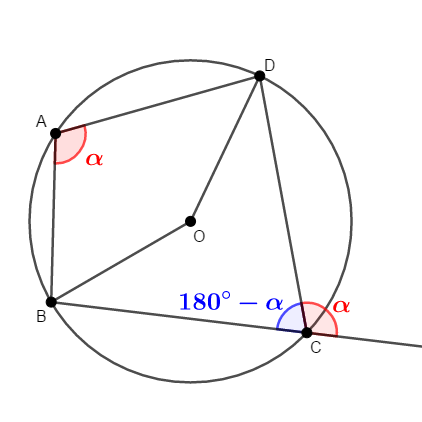
四角形が円に内接する条件
さて,円に内接する四角形の性質を考えましたが,実は前項で学んだ定理は,逆も成り立ちます。 逆は,四角形が円に内接するための条件として使えます。
四角形が円に内接するとは,四角形の\(4\)頂点がすべて同一円周上にあるということです。 このように,いくつかの点が同一円周上にあるとき,それらの点を共円であるといいます。
次のいずれかが成り立つ四角形は,円に内接する。 (その\(4\)頂点は共円である。)
- 対角の和が\(180^{\circ}\)である。
- 内角とその対角の外角が等しい。
こちらも証明しましょう。 \(2\)つの条件は同じ意味ですから,\(1\)つめの条件について証明すれば十分ですね。
対角の和が\(180^{\circ}\)である四角形\(\mathrm{ABCD}\)を考えます。 この四角形が円に内接することを示すには,\(4\)頂点が共円であることを示せば良く,そのためには,同じ弧に対する円周角に相当する角が等しいことを示せば良かったですね。
ところで,三角形に必ず外接円が存在することは,既に学びました。 せっかくなので,これも利用しましょう。 \(\triangle\mathrm{ABC}\)の外接円\(\mathrm{O}\)を考えます。
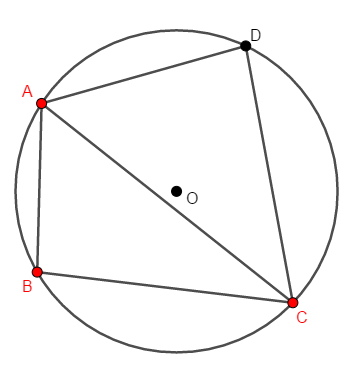
現時点で\(3\)頂点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)は円\(\mathrm{O}\)の周上にあることが分かっています。 あとは頂点\(\mathrm{D}\)も円\(\mathrm{O}\)の周上にあることを確認すれば良いです。
ここで,仮定より\(\angle\mathrm{B} + \angle\mathrm{D} = 180^{\circ}\)であることを思い出しましょう。
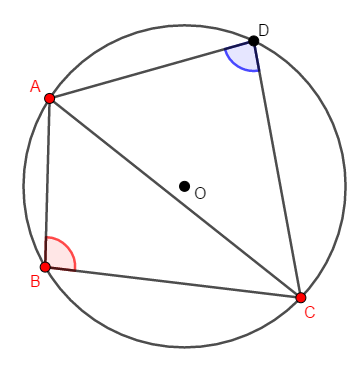
仮定はこれだけですから,この情報を活用する必要があります。 そこで,次のように円周上の点\(\mathrm{D}'\)をとり,弧\(\mathrm{ABC}\)に対する円周角\(\angle\mathrm{AD}'\mathrm{C}\)を考えましょう。
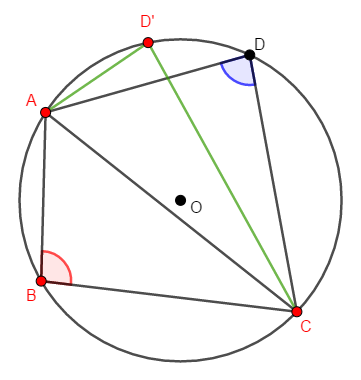
この時点では,\(\mathrm{D}\)はまだ円周上の点かどうか分からないことに注意してください。 図では,円周上にあると分かっている点を赤色で表しています。
さて,四角形\(\mathrm{ABCD}'\)は円\(\mathrm{O}\)に内接する四角形ですから,対角の和が\(180^{\circ}\)です。 したがって,\(\angle\mathrm{D}' + \angle\mathrm{B} = 180^{\circ}\)です。 さらに,仮定より\(\angle\mathrm{D} + \angle\mathrm{B} = 180^{\circ}\)ですから,\(\angle\mathrm{D} = \angle\mathrm{D}'\)が成り立ちます。
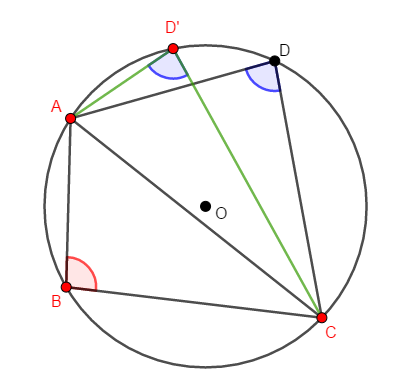
これで直線\(\mathrm{AC}\)に関して同じ側にある点\(\mathrm{D}\),\(\mathrm{D}'\)について,\(\angle\mathrm{AD}'\mathrm{C} = \angle\mathrm{ADC}\)が成り立つので,\(4\)点\(\mathrm{A}\),\(\mathrm{C}\),\(\mathrm{D}'\),\(\mathrm{D}\)が共円であることが示されました。
同時に\(4\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\),\(\mathrm{D}\)が共円であることも分かりました。 つまり四角形\(\mathrm{ABCD}\)が円\(\mathrm{O}\)の内接円であることが証明できたのです。
確認問題
次の図で,四角形\(\mathrm{ABCD}\)は円に内接しています。 \(\angle\mathrm{ABC}\)を求めてください。

答え
\(\angle\mathrm{ABC} = \theta\)とします。 \(\angle\mathrm{ABC}\)とその対角の外角は等しいので,\(\angle\mathrm{CDQ} = \theta\)です。
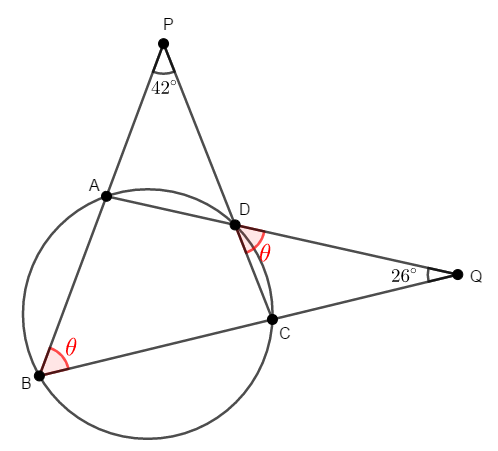
\(\triangle\mathrm{CDQ}\)の内角が\(2\)つ揃ったので,残りの角での外角が分かります。 \(\angle\mathrm{DCB} = \theta + 26^{\circ}\)ですね。
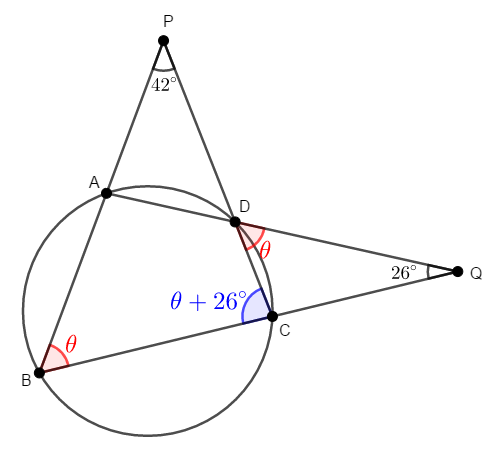
今度は\(\triangle\mathrm{BCP}\)の内角がすべて揃いました。 三角形の内角の和は\(180^{\circ}\)ですから,次が成り立ちますね。
以上から,\(\angle\mathrm{ABC} = 56^{\circ}\)です。 等しい角を見つけ,角が揃った三角形に注目するなどすれば,簡単ですね。
下図で,点\(\mathrm{X}\)は\(\triangle\mathrm{ABC}\)の外接円上の点です。 また,点\(\mathrm{X}\)から直線\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)に下ろした垂線をそれぞれ\(\mathrm{XP}\),\(\mathrm{XQ}\),\(\mathrm{XR}\)としています。
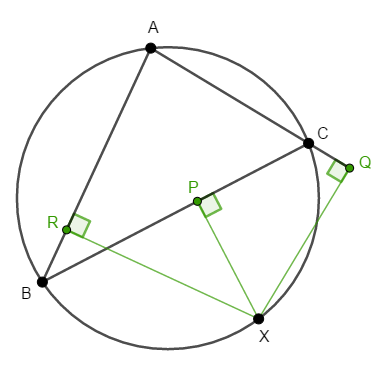
このとき,\(3\)点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が共線であることを証明したいと思います。 次の問いに答えて下さい。
-
\(\angle\mathrm{ABX} = \angle\mathrm{QCX}\)を証明してください。
-
\(\angle\mathrm{QCX} = \angle\mathrm{XPQ}\)を証明してください。
-
\(3\)点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が共線であることを証明してください。
答え
円に内接する四角形について成り立つこと,四角形が円に内接するための条件などをうまく活用します。 角度の情報がたくさん得られるので,\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)の共線については,\(\angle\mathrm{RPQ} = 180^{\circ}\)を示すと良いです。
この手の問題は,図がごちゃごちゃしがちです。 そんなときは,\(1\)つの図に全ての情報を書き込むのではなく,適宜必要な部分だけを抜き出した図をかくと整理しやすいです。
-
\(\angle\mathrm{ABX}\),\(\angle\mathrm{QCX}\)の周辺の図形に注目すると,四角形\(\mathrm{ABXC}\)が見つかります。 この四角形は\(\triangle\mathrm{ABC}\)の外接円に内接していますから,内角とその対角の外角は等しいです。 したがって,\(\angle\mathrm{ABX} = \angle\mathrm{QCX}\)です。
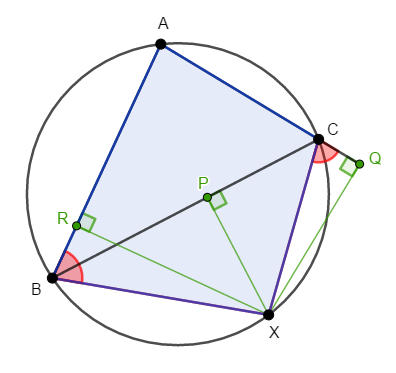
-
問題の角を図にかくと分かる通り,この\(2\)つの角は,共通の弧に対する円周角っぽい形です。
実際,四角形\(\mathrm{XPCQ}\)について\(\angle\mathrm{XPC} + \angle\mathrm{CQX} = 180^{\circ}\)が成り立ちますから,対角の和が\(180^{\circ}\)なのでこれは円に内接します。
したがって,同一の弧\(\mathrm{XQ}\)に対する円周角\(\angle\mathrm{QCX}\)と\(\angle\mathrm{XPQ}\)は等しいです。
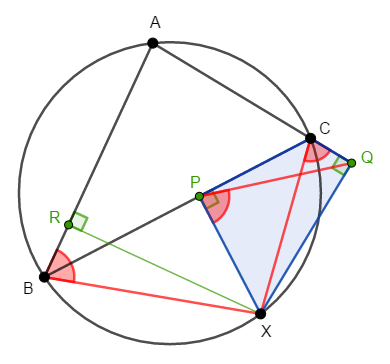
-
角度の情報がいろいろ出てきましたから,\(\angle\mathrm{RPQ} = 180^{\circ}\)を証明することにしましょう。 \(\angle\mathrm{RPQ} = \angle\mathrm{RPX} + \angle\mathrm{XPQ}\)ですが,(1)と(2)により,\(\angle\mathrm{XPQ} = \angle\mathrm{RBX}\)であることは分かっています。
そこで,これらの角が関わる四角形\(\mathrm{BRPX}\)に注目しましょう。 (同一の弧に対する円周角に相当する)角\(\angle\mathrm{BRX}\)と\(\angle\mathrm{BPX}\)がともに直角で等しく,\(2\)点\(\mathrm{R}\),\(\mathrm{P}\)が直線\(\mathrm{BX}\)に関して同じ側にあるため,四角形\(\mathrm{BRPX}\)は円に内接することが分かります。
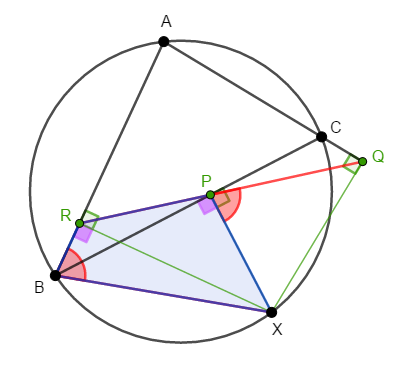
したがって,この四角形の対角の和は\(180^{\circ}\)ですから,\(\angle\mathrm{RBX}\)と\(\angle\mathrm{RPX}\)の和は\(180^{\circ}\)です。 ここで,\(\angle\mathrm{RBX}\)と\(\angle\mathrm{XPQ}\)は等しかったのですから,\(\angle\mathrm{RPX}\)と\(\angle\mathrm{XPQ}\)の和も\(180^{\circ}\)です。
以上から,\(\angle\mathrm{RPX} = 180^{\circ}\)であり,\(3\)点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が共線であることが示されました。
これを一般化したのがシムソンの定理です。
