目次

• 円と直線の位置関係
• 円の接線
• 確認問題

円と直線の位置関係

まずは円と直線がともにあるとき，どんな位置関係があるか考えてみましょう。 次図のように直線と円が離れた状態から考えて，少しずつ円に近づけてみましょう。

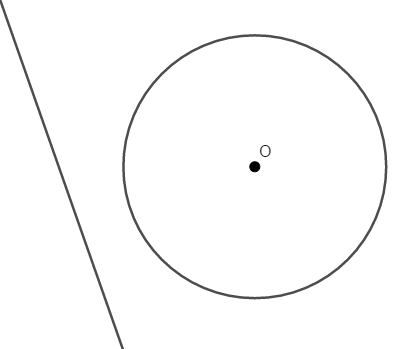
この図の状況では，円と直線に共有点はありません。 さらに直線を円に近づけていくと，やがて直線は円にぶつかります。

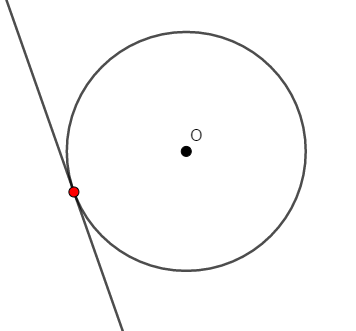
この図の状況では，円と直線には\(1\)つだけ共有点があります。 直線が円に接している状況ですね。 このように円に接する直線を接線といいます。

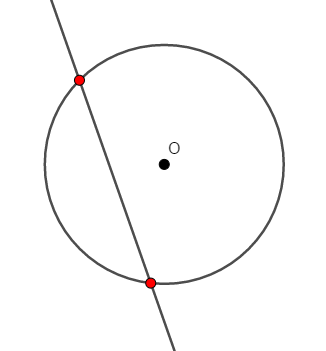
もう少し直線を円に近づけると，次図のように，円と直線の共有点は\(2\)つになります。 このように円と\(2\)点で交わる直線を割線といいます。

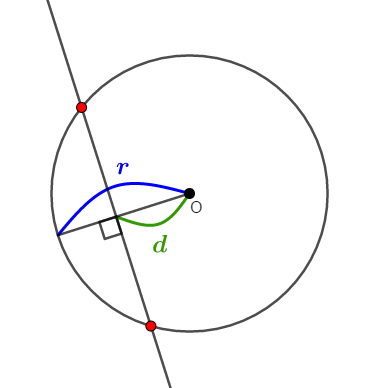
円と直線の位置関係は，このように共有点\(0\)～\(2\)個の\(3\)通りです。 円の半径を\(r\)，円の中心と直線の距離を\(d\)とすると，次のように整理できます。

円と直線の位置関係

円と直線の位置関係は，円の半径を\(r\)，円の中心と直線の距離を\(d\)とすると，次の\(3\)通りある。

\(d\)と\(r\)の大小	共有点の個数	位置関係
\(d > r\)	\(0\)	離れている
\(d = r\)	\(1\)	接する
\(d < r\)	\(2\)	\(2\)点で交わる

円の接線

円と直線の位置関係のうち，特に重要なのが接する場合です。 円に接する直線を接線といい，円と接線の共有点を接点といいましたね。

円と接線に関する次の定理も思い出しておきましょう。

円の半径と接線

円の接線は，その接点を通る半径に垂直である。

逆も成り立ち，円周上の点を通る直線がその点を通る半径に垂直であるとき，この直線はこの円の接線である。

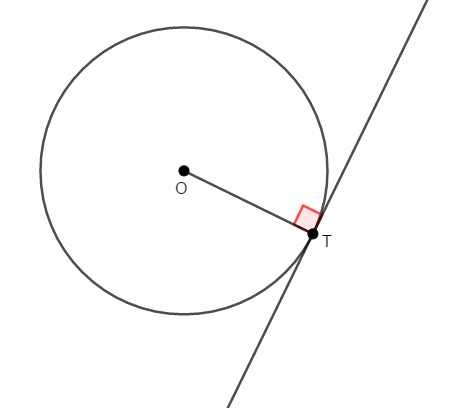
今回円の接線に関して新しく考えることは，「円の外部の点から円に接線を引くとどうなるか」です。 次図の通り，接線は\(2\)本引けます。

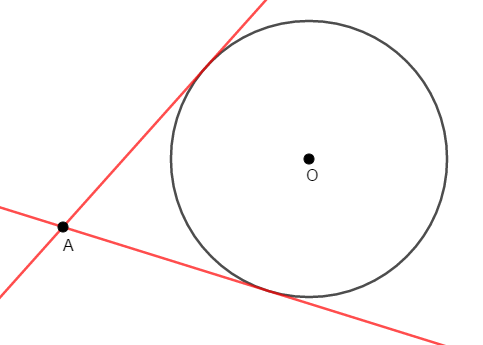
このように円の外部から円に接線を引いたとき，その点と接点の距離を接線の長さといいます。

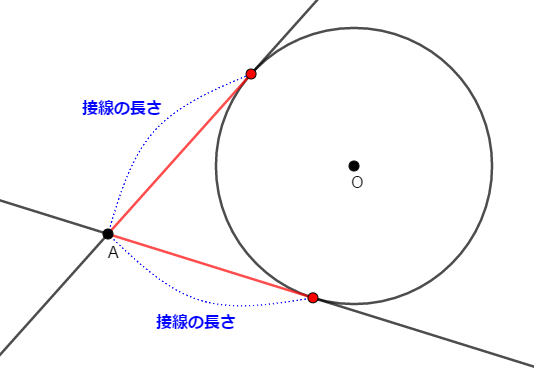
図の見た目からも想像がつく通り，接線の長さについて次が成り立ちます。

もちろん見た目だけで判断してはいけませんから，証明しましょう。 円\(\mathrm{O}\)に外部の点\(\mathrm{A}\)から接線を引き，\(2\)つの接点を\(\mathrm{P}\)，\(\mathrm{Q}\)とします。

このとき，線分\(\mathrm{OP}\)，\(\mathrm{OQ}\)はそれぞれ接線\(\mathrm{AP}\)，\(\mathrm{AQ}\)に垂直であり，どちらも円\(\mathrm{O}\)の半径ですから，同じ長さです。

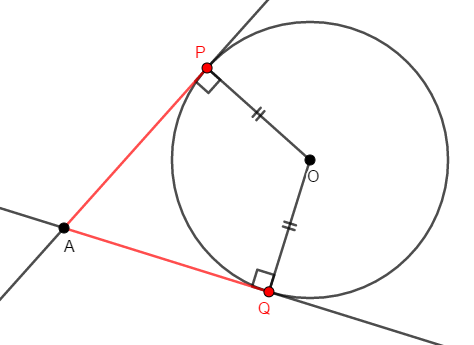
証明したいのは\(\mathrm{AP} = \mathrm{AQ}\)ですが，線分の長さが等しいことを示すには，三角形の合同を利用できます。 線分\(\mathrm{AO}\)を引き，\(2\)つの直角三角形を作りましょう。

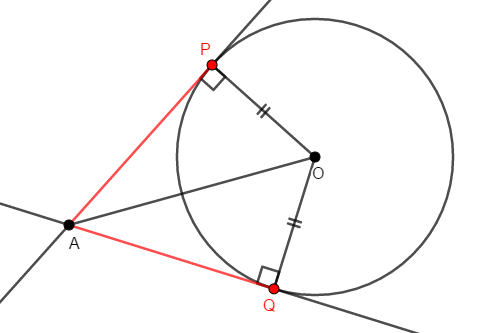
\(2\)つの直角三角形\(\triangle\mathrm{OAP}\)，\(\triangle\mathrm{OAQ}\)は斜辺が共通であり，\(\mathrm{OP} = \mathrm{OQ}\)ですから，斜辺と他の\(1\)辺がそれぞれ等しいので，これらは合同です。 したがって，対応する辺が等しいので，\(\mathrm{AP} = \mathrm{AQ}\)です。

これで上の定理が証明できましたね。 あとは簡単な確認問題を解いて，自然に使いこなせるようにしましょう。

確認問題

半径\(5\)の円\(\mathrm{O}\)と，この円の中心からの距離が\(7\)である点\(\mathrm{P}\)があります。 点\(\mathrm{P}\)から円\(\mathrm{O}\)に引いた接線の長さを答えてください。

答え

まず図をかきましょう。 \(2\)つの接点を\(\mathrm{A}\)，\(\mathrm{B}\)とします。

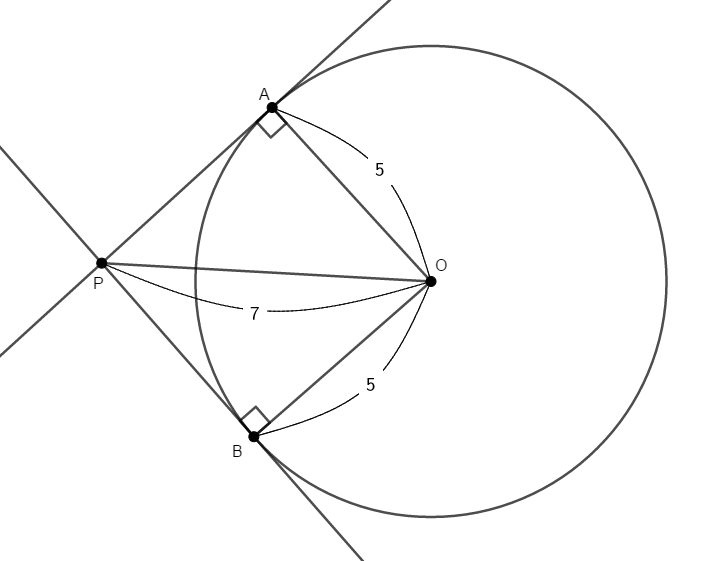
接線の長さとは\(\mathrm{PA} = \mathrm{PB}\)の長さのことですが，図をかけばすぐ分かりますね。 直角三角形\(\mathrm{OAP}\)で三平方の定理を使いましょう。

\( \begin{align} \mathrm{OA}^2 + \mathrm{PA}^2 &= \mathrm{OP}^2 \\[5pt] 5^2 + \mathrm{PA}^2 &= 7^2 \\[5pt] \mathrm{PA}^2 &= 7^2 - 5^2 \\[5pt] &= 24 \\[5pt] \end{align} \)

\(\mathrm{PA} > 0\)ですから，\(\mathrm{PA} = 2\sqrt{6}\)ですね。 したがって，求める接線の長さは\(2\sqrt{6}\)です。

\(\triangle\mathrm{ABC}\)の内接円が辺\(\mathrm{BC}\)，\(\mathrm{CA}\)，\(\mathrm{AB}\)と接する点をそれぞれ\(\mathrm{P}\)，\(\mathrm{Q}\)，\(\mathrm{R}\)とします。

\(\mathrm{BC} = 6\)，\(\mathrm{CA} = 5\)，\(\mathrm{AB} = 7\)とするとき，\(\mathrm{AR}\)，\(\mathrm{BP}\)，\(\mathrm{CQ}\)の長さを求めてください。

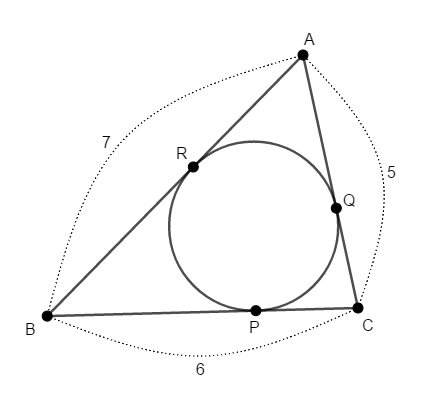
答え

\(\mathrm{AR}\)，\(\mathrm{BP}\)，\(\mathrm{CQ}\)の長さは，それぞれ点\(\mathrm{A}\)，\(\mathrm{B}\)，\(\mathrm{C}\)から\(\triangle\mathrm{ABC}\)の内接円に引いた接線の長さです。

\(1\)点から円に引いた\(2\)本の接線の長さは等しいので，\(\mathrm{AR} = \mathrm{AQ}\)，\(\mathrm{BP} = \mathrm{BR}\)，\(\mathrm{CQ} = \mathrm{CP}\)です。 \(\mathrm{AR} = x\)，\(\mathrm{BP} = y\)，\(\mathrm{CQ} = z\)とすると，これは次の図にまとめられます。

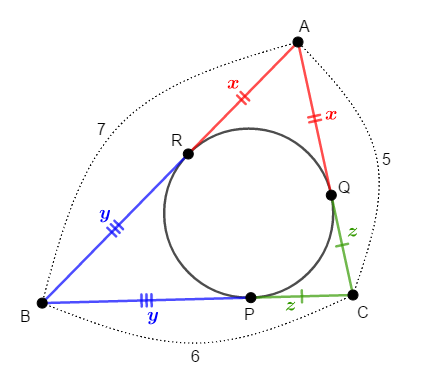
各辺の長さは分かっていますから，次の連立方程式が成り立ちます。

\( \begin{eqnarray} \left\{ \begin{array}{l} x + y &= 7 \\ y + z &= 6 \\ z + x &= 5 \end{array} \right. \end{eqnarray} \)

あとは\(x\)，\(y\)，\(z\)を求めるだけですが，連立方程式が見慣れない形をしているかもしれません。 連立方程式を解くには，とにかく文字の種類を減らす必要がありますから，\(1\)つめの式を\(x = 7 - y\)，\(2\)つめの式を\(z = 6 - y\)と変形して，それぞれ\(3\)つめの式に代入すれば良いです。 これで\(y\)だけの式になるので，\(y\)が求められますね。

ここでは別の解き方を紹介します。 \(3\)つの式を辺々足すと，次の式が得られます。

\( \begin{align} 2x + 2y + 2z &= 7 + 6 + 5 \\[5pt] 2(x + y + z) &= 18 \\[5pt] x + y + z &= 9 \end{align} \)

これに\(1\)つめの式の\(x + y = 7\)を代入すれば，次のようになります。

\( \begin{align} 7 + z &= 9 \\[5pt] z &= 2 \end{align} \)

同様に\(2\)つめ，\(3\)つめの式を代入すれば，それぞれの方程式から\(x = 3\)，\(y = 4\)と求められます。

以上から，\(\mathrm{AR} = 3\)，\(\mathrm{BP} = 4\)，\(\mathrm{CQ} = 2\)です。