前回,円の接線について簡単な性質を学びました。 今回は円と接線に関して重要な「接弦定理」を学びます。
目次
接弦定理
円の接線と弦が作る角に関する定理が接弦定理です。 慣れないとピンと来ないかもしれませんが,まずは内容を確認してみましょう。
円周上の\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)と点\(\mathrm{A}\)における接線を考える。 また,この接線上の,弦\(\mathrm{AB}\)に関して\(\mathrm{C}\)と反対側に点\(\mathrm{X}\)をとる。
このとき,次が成り立つ。
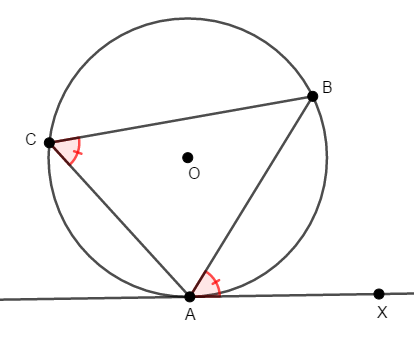
何だかややこしい気もしますが,とにかく上図の状況を頭に入れておきましょう。 これを文字で説明すると複雑な感じがするだけです。
イメージとしては,円周角の定理の延長のようなものと考えれば,覚えやすいです。 次図のように,\(\mathrm{C}\)と\(\mathrm{A}\)の間の弧上に点\(\mathrm{P}\)をとりましょう。 円周角の定理により,\(\angle\mathrm{ACB} = \angle\mathrm{APB}\)ですね。
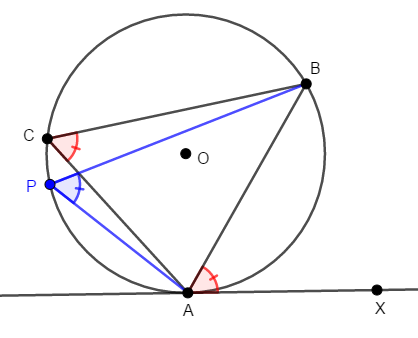
\(\mathrm{P}\)をさらに\(\mathrm{A}\)に近づけていくとどうなるでしょうか? 次図を見てください。
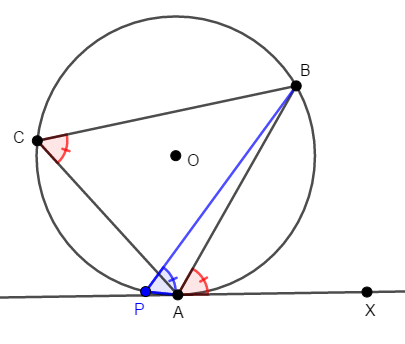
もう接弦定理に近い形になっていますね。 こうして\(\mathrm{P}\)をどこまでも\(\mathrm{A}\)に近づけていくと,直線\(\mathrm{PA}\)は実質\(\mathrm{A}\)での接線になり,接弦定理と同じ形になります。
こう考えれば,円周角の定理の延長のようなものとして,接弦定理を覚えられます。
では接弦定理の証明を始めましょう。 \(\angle\mathrm{BAX}\)が鋭角・直角・鈍角の場合に分けて考えます。
[1] まずは簡単な場合から始めたいので,\(\angle\mathrm{BAX}\)が直角の場合を考えましょう。
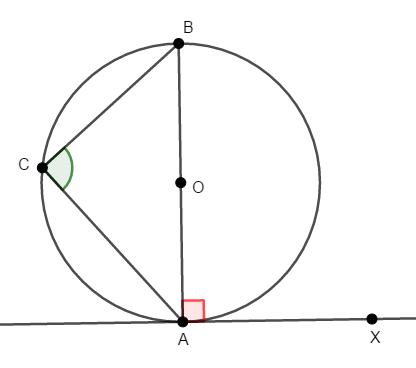
このとき,線分\(\mathrm{AB}\)は円\(\mathrm{O}\)の直径です。 ということは,タレスの定理により,\(\angle\mathrm{ACB}\)も直角であり,\(\angle\mathrm{BAX} = \angle\mathrm{ACB}\)が成り立つことが分かります。
[2] 次は\(\angle\mathrm{BAX}\)が鋭角の場合を考えます。 初めに見た図の状況ですね。 先ほど直角の場合を証明しましたから,それと同じように考えるため,次図のように直径\(\mathrm{AD}\)をかきましょう。
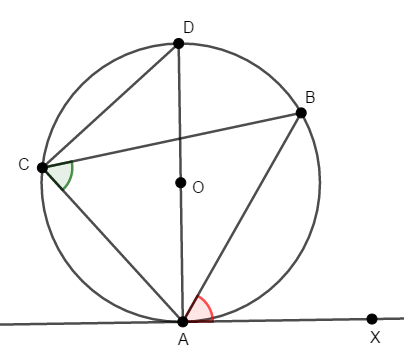
このとき\(\angle\mathrm{DAX}\)は,接線とその接点を通る半径のなす角なので,直角です。 また,タレスの定理により,\(\angle\mathrm{ACD}\)も直角であり,\(\angle\mathrm{DAX} = \angle\mathrm{ACD}\)が成り立ちます。
さらに,弧\(\mathrm{BD}\)に対する円周角の定理により,\(\angle\mathrm{BAD} = \angle\mathrm{BCD}\)です。

これで次のようにして,\(\angle\mathrm{BAX} = \angle\mathrm{ACB}\)が成り立つことが分かります。
[3] 最後に\(\angle\mathrm{BAX}\)が鈍角の場合を考えましょう。
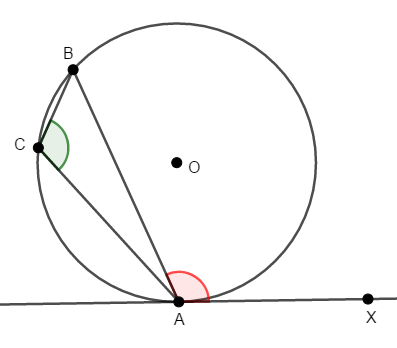
このとき,\(\angle\mathrm{BAX}\)の反対側の角は鋭角になりますから,先ほど証明した鋭角の場合の接弦定理を利用できます。
接線上の,\(\mathrm{A}\)から見て\(\mathrm{X}\)の反対側に点\(\mathrm{Y}\)をとりましょう。 \(\angle\mathrm{CAY}\)は鋭角ですから,先ほど証明した鋭角の場合の接弦定理により,\(\angle\mathrm{CAY} = \angle\mathrm{ABC}\)です。
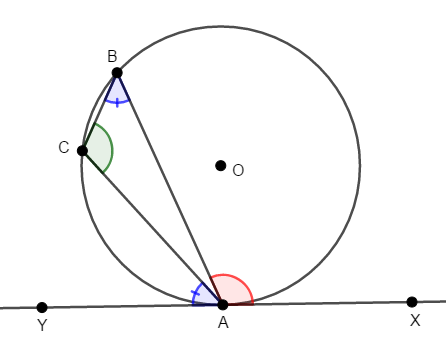
あとは\(\triangle\mathrm{ABC}\)の内角の和が\(180^{\circ}\)であることと,\(\angle\mathrm{YAX} = 180^{\circ}\)であることに注目すれば,\(\angle\mathrm{BAX} = \angle\mathrm{ACB}\)が成り立つことが分かります。
これで接弦定理が証明できました! この定理は逆も成り立ち,重要ですから,引き続き次項で確認していきましょう。
接弦定理の逆
接弦定理の逆は,円周上の点を通る直線が,その円の接線であることを示すのに役立ちます。 その内容は,次の通りです。
円\(\mathrm{O}\)の円周上に\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)がある状況を考える。
点\(\mathrm{A}\)を通る直線上の,弦\(\mathrm{AB}\)に関して\(\mathrm{C}\)と反対側に点\(\mathrm{X}\)をとり,次の等式が成り立つとき,この直線は円\(\mathrm{O}\)の接線である。
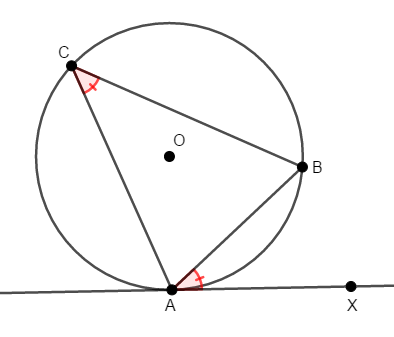
定理の内容だけ読むとややこしい感じですが,接弦定理が頭に入っていればすぐ理解できます。 接弦定理は接線を考えたときに角度の等式が成り立ちますが,その逆は,角度の等式が成り立つときに接線が見つかります。
証明を始めます。 接弦定理が成り立つことは先ほど証明しましたから,これをうまく活用します。 点\(\mathrm{A}\)での円\(\mathrm{O}\)の接線を引くのです。 また,この接線上の,弦\(\mathrm{AB}\)に関して\(\mathrm{C}\)と反対側に点\(\mathrm{Y}\)をとります。
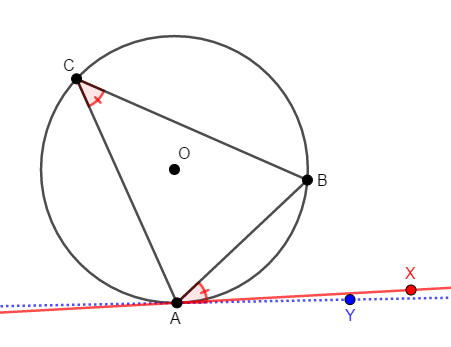
上図では,元からある直線を赤い実線で,新しく追加した接線を青い点線で表しています。 この\(2\)直線が一致することを示しましょう。 (見やすさのため,図ではずらしてかいています。)
どうやってこれを示すかですが,接弦定理を利用することを考えると,\(\angle\mathrm{BAX} = \angle\mathrm{BAY}\)を示すのが簡単そうですね。 ただしこの等式を示すだけでは十分ではありません。
例えば次図の状況では,この等式は成り立つものの,\(2\)直線は一致しません。
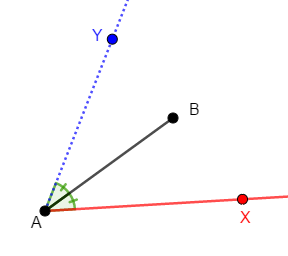
この図で\(2\)直線が一致しないのでは,点\(\mathrm{X}\),\(\mathrm{Y}\)が直線\(\mathrm{AB}\)に関して反対側にあるからです。 \(\angle\mathrm{BA}\Box\)を考えるとき,点\(\Box\)のとり方が\(2\)通りあることに注意する必要があります。
さて,今回の証明の場合については,点\(\mathrm{X}\),\(\mathrm{Y}\)は,共に弦\(\mathrm{AB}\)に関して同じ側にありますから,この点はOKです。 両方とも弦\(\mathrm{AB}\)に関して\(\mathrm{C}\)と反対側にあるからです。 したがって,やはり\(\angle\mathrm{BAX} = \angle\mathrm{BAY}\)を示せば,\(2\)直線が一致することを示せます。
直線\(\mathrm{AY}\)は接線ですから,\(\angle\mathrm{BAY}\)については,接弦定理により\(\angle\mathrm{BAY} = \angle\mathrm{ACB}\)が成り立ちます。
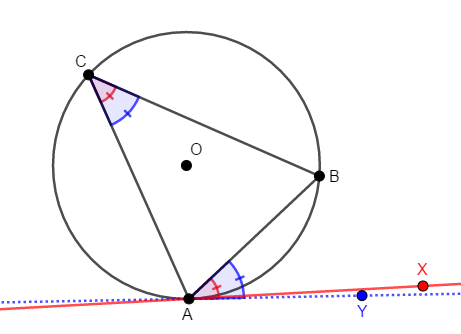
ここで,仮定より\(\angle\mathrm{BAX} = \angle\mathrm{ACB}\)ですから,次の通り\(\angle\mathrm{BAX} = \angle\mathrm{BAY}\)が成り立つことが分かります。
これで\(2\)直線が一致することが分かったので,直線\(\mathrm{AX}\)は円\(\mathrm{O}\)の接線です。
接弦定理の逆は,ある直線が円の接線であることを証明するのに役立つ道具です。 使えるようにしておきましょう。
確認問題
次の図で,半直線\(\mathrm{XA}\),\(\mathrm{XB}\)は円\(\mathrm{O}\)の接線であり,点\(\mathrm{A}\),\(\mathrm{B}\)はそれぞれの接点です。 このとき,\(\angle\mathrm{CAB}\)を求めてください。
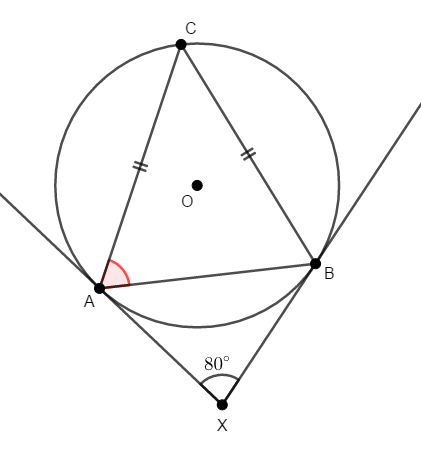
答え
円の外部から円に引いた接線の長さは等しいので,\(\mathrm{XA} = \mathrm{XB}\)であり,\(\triangle\mathrm{XAB}\)は二等辺三角形です。 その底角は\(\displaystyle\frac{180^{\circ} - 80^{\circ}}{2} = 50^{\circ}\)です。
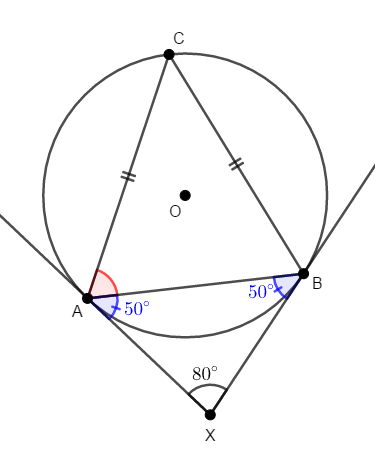
さらに接弦定理により,\(\angle\mathrm{XAB} = \angle\mathrm{ACB}\)です。
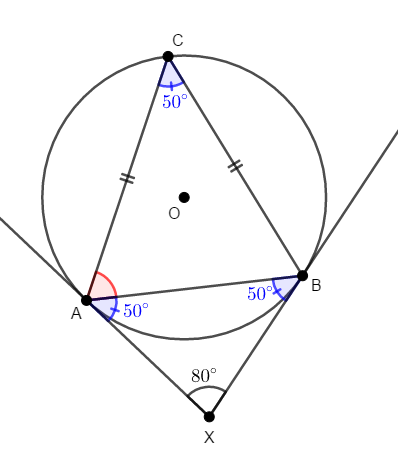
\(\triangle\mathrm{CAB}\)も二等辺三角形であり,\(\angle\mathrm{CAB}\)はその底角ですから,その角度は\(\displaystyle\frac{180^{\circ} - 50^{\circ}}{2} = 65^{\circ}\)です。 以上から,\(\angle\mathrm{CAB} = 65^{\circ}\)です。
正三角形\(\mathrm{ABC}\)の辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)を\(m : n\)に内分する点をそれぞれ\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)とします。 ただし\(m\),\(n\)は正の数です。
このとき,直線\(\mathrm{RP}\)が,\(3\)点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{C}\)を通る円の接線であることを証明してください。
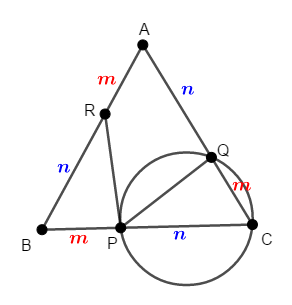
答え
まず何をすべきか,はっきりさせましょう。 円周上の点\(\mathrm{X}\)を通る直線がその円の接線であることを示すには,今のところ次の\(2\)つの方法があります。
- 直線が,\(\mathrm{X}\)を通る円の半径と垂直であることを示す。
- 直線と円の弦に対して,接弦定理の逆を利用する。
この問題では,円の中心が分からないので,半径も分かりません。 接弦定理の逆を利用した方が楽そうです。
題意を接弦定理の逆を利用して示すため,\(\angle\mathrm{RPQ} = \angle\mathrm{PCQ}\)が成り立つことを証明します。
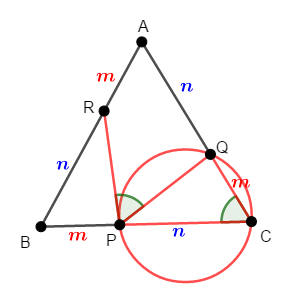
\(\triangle\mathrm{ABC}\)は正三角形ですから,\(\angle\mathrm{PCQ} = \angle\mathrm{BCA} = 60^{\circ}\)です。 ですから,\(\angle\mathrm{RPQ} = 60^{\circ}\)を示せば良いですね。
図を見ると,\(\triangle\mathrm{PQR}\)は正三角形になりそうですね。 \(3\)頂点がバランスよく配置されているからです。 実際に正三角形であることを確認すれば,\(\angle\mathrm{RPQ} = 60^{\circ}\)も示せますね。
次図のように\(\triangle\mathrm{AQR}\),\(\triangle\mathrm{BRP}\),\(\triangle\mathrm{CPQ}\)に注目します。
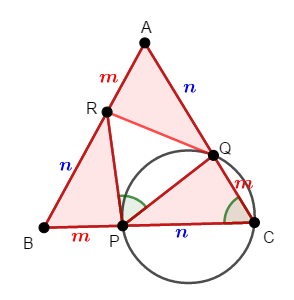
\(\triangle\mathrm{ABC}\)の\(1\)辺の長さを\(a\)とすると,次が成り立ちます。
以上から,\(2\)辺とその間の角がそれぞれ等しいので,\(\triangle\mathrm{AQR}\),\(\triangle\mathrm{BRP}\),\(\triangle\mathrm{CPQ}\)は合同です。 よって,対応する辺の長さが等しいため,\(\mathrm{PQ} = \mathrm{QR} = \mathrm{RP}\)が成り立ちます。
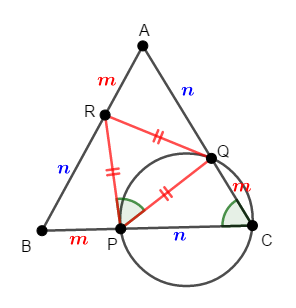
したがって,\(\triangle\mathrm{PQR}\)は正三角形であるため,\(\angle\mathrm{RPQ} = 60^{\circ}\)です。
以上から,\(\angle\mathrm{RPQ} = \angle\mathrm{PCQ}\)であり,点\(\mathrm{C}\)と点\(\mathrm{R}\)が弦\(\mathrm{PQ}\)に関して反対側にあるため,接弦定理の逆により,直線\(\mathrm{RP}\)は\(3\)点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{C}\)を通る円の接線です。
