これまで円と直線,特に接線の関係を見てきました。 今回は\(1\)つの円に対して,\(1\)点を通り円と交わる\(2\)直線を考え,この状況で成り立つ「方べきの定理」を学びます。
目次
方べきの定理
早速ですが,方べきの定理の内容を見てみましょう。
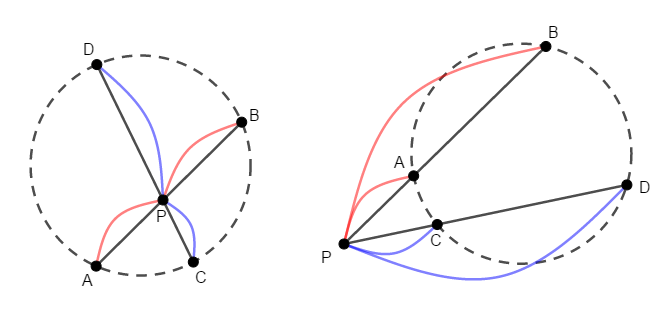
円の\(2\)つの弦\(\mathrm{AB}\),\(\mathrm{CD}\)またはその延長の交点を\(\mathrm{P}\)とすると,次の式が成り立つ。
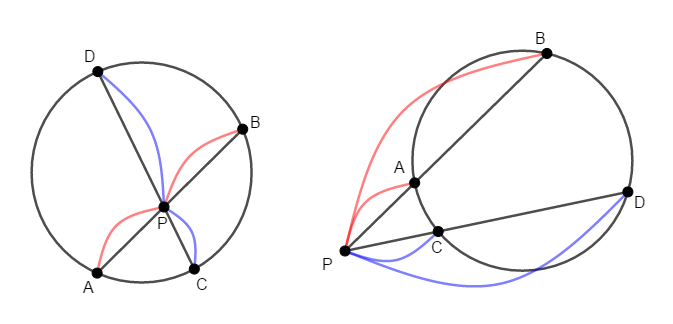
この定理は,上図の通り\(\mathrm{AB}\),\(\mathrm{CD}\)が円の外部で交わる場合にも成り立ちます。 また,見方を変えれば,これは\(1\)つの円と\(1\)点で交わる\(2\)本の円の割線に関する定理です。 円と\(2\)点で交わる直線を割線といいましたね。
では方べきの定理を証明しましょう。 線分の積について成り立つ等式を証明したいのですが,これは次のように比の式に書き換えられます。
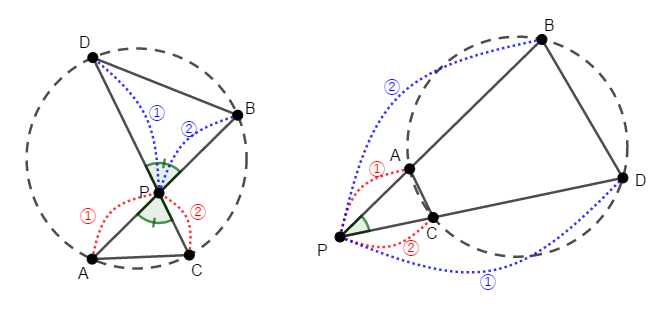
というわけで,この比の式が成り立つことを証明すれば良く,比の式を作るには三角形の相似に注目すれば良いですね。 線分\(\mathrm{AC}\),\(\mathrm{BD}\)を引き,\(2\)つの三角形を作りましょう。
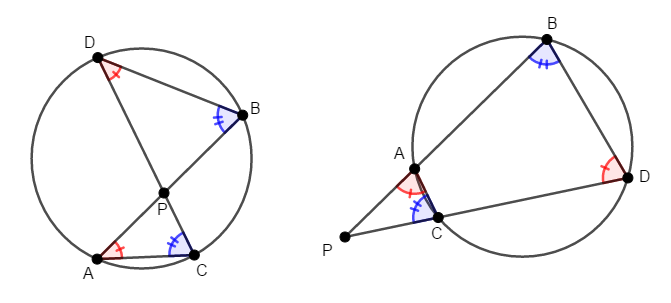
このとき,左右どちらの図でも\(\angle\mathrm{PAC} = \angle\mathrm{PDB}\),\(\angle\mathrm{PCA} = \angle\mathrm{PBD}\)が成り立ちます。 左の図では円周角の定理,右の図では円に内接する四角形の内角が,その対角の外角と等しいことを利用すれば分かりますね。
したがって,\(2\)組の角がそれぞれ等しいので,\(\triangle\mathrm{PAC}\)と\(\triangle\mathrm{PDB}\)は相似です。 相似であれば対応する辺の比が等しいのですから,次の式が成り立ちます。
これで方べきの定理が証明できました。 ところで,方べきの定理にはもうひとつ重要な形があります。 次のように,直線の\(1\)つが接線になっている場合です。
円周上の点\(\mathrm{T}\)を通る接線と弦\(\mathrm{AB}\)の延長の交点を\(\mathrm{P}\)とすると,次の式が成り立つ。
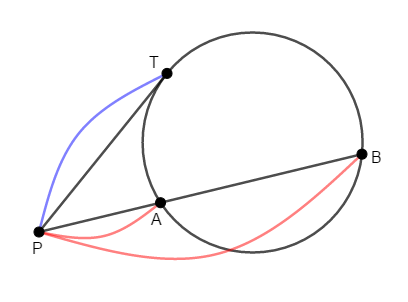
初めに見た方べきの定理で,\(\mathrm{PC}\)と\(\mathrm{PD}\)が一緒になった場合と考えれば良いです。 では証明を始めましょう。
証明の方針は変わりません。 次の比の式が成り立つことを証明すれば良いですね。
この比を得るため,三角形の相似を考えます。 線分\(\mathrm{AT}\)を引いて\(2\)つの三角形を作りましょう。
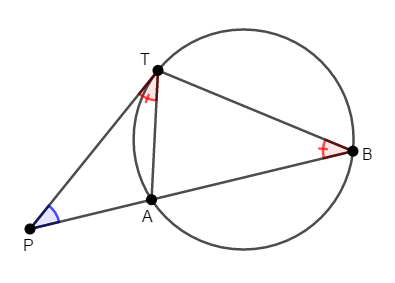
このとき,接弦定理により,\(\angle\mathrm{PTA} = \angle\mathrm{PBT}\)が成り立つことが分かります。 さらに\(\angle\mathrm{TPA} = \angle\mathrm{BPT}\)が共通することから,\(2\)組の角がそれぞれ等しいので,\(\triangle\mathrm{PTA}\)と\(\triangle\mathrm{PBT}\)は相似です。 したがって,対応する辺の比が等しいので,次が成り立ちます。
これでこの場合の方べきの定理が成り立つことも分かりました。 この定理は逆も成り立ち,重要ですから,次項で確認していきます。
方べきの定理で\(2\)直線が両方とも円の接線であるとき,どうなるのでしょうか? 円の外部の点\(\mathrm{P}\)から円に\(2\)本の接線を引き,接点を\(\mathrm{S}\),\(\mathrm{T}\)としましょう。
このとき成り立つ式は,次の通りです。 以前学んだ「接線の長さは等しい」という事実ですね。
方べきの定理の式の形に合わせるなら,\(\mathrm{PS}^2 = \mathrm{PT}^2\)ともいえます。
方べきの定理の逆
方べきの定理の逆は,次の内容です。
\(2\)つの線分\(\mathrm{AB}\),\(\mathrm{CD}\)またはその延長の交点を\(\mathrm{P}\)とする。
このとき,次の式が成り立つならば,\(4\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\),\(\mathrm{D}\)は共円である。 (同一円周上にある。)
円周角の定理の逆,四角形が円に内接する条件に続いて,これもまた\(4\)点の共円条件になっています。 線分の長さや比が分かる状況では,この定理を利用して共線を示せます。
では証明に入ります。 左図では円周角の定理の逆を使い,右図では四角形\(\mathrm{ACDB}\)がある円の内接円であることを証明すれば良いでしょう。 つまり左図では円周角に相当する角が等しいことを示し,右図ではある内角とその対角の外角が等しいことを証明します。
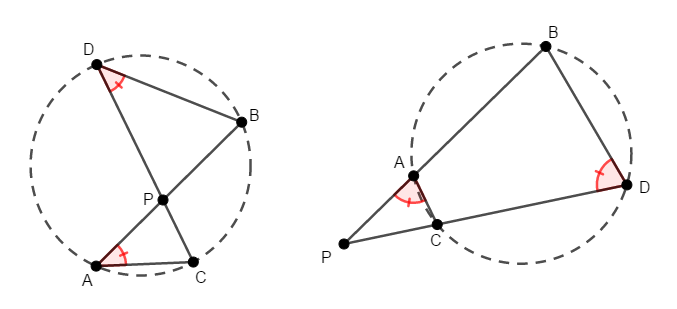
角度の等式を得るためには,やはり三角形の相似が役立つでしょう。 定理の条件により,次の比の式が成り立つことを確認してください。
また,左右どちらの図でも\(\angle\mathrm{APC} = \angle\mathrm{DPB}\)が成り立ちます。 左図では対頂角同士なので,右図では共通の角だからですね。
したがって,\(2\)組の辺の比とその間の角が等しいので,\(\triangle\mathrm{PAC}\)と\(\triangle\mathrm{PDB}\)は相似です。 相似であれば対応する角が等しいのですから,次の式が成り立ちます。
これで,左図では円周角に相当する角が等しいこと,つまり直線\(\mathrm{BC}\)について同じ側にある点\(\mathrm{A}\),\(\mathrm{D}\)について,上の式が成り立つことが分かったので,\(4\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\),\(\mathrm{D}\)が共円であることが分かりました。
右図については,四角形\(\mathrm{ACDB}\)の内角\(\angle\mathrm{D}\)が,その対角の外角\(\angle\mathrm{PAC}\)と等しいことが分かったわけですから,四角形\(\mathrm{ACDB}\)は円に内接する,つまり\(4\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\),\(\mathrm{D}\)が共円であることが分かりました。
これで方べきの定理の逆が証明できましたが,方べきの定理にはもうひとつ重要な形があるのでした。 その逆も確認しておきましょう。
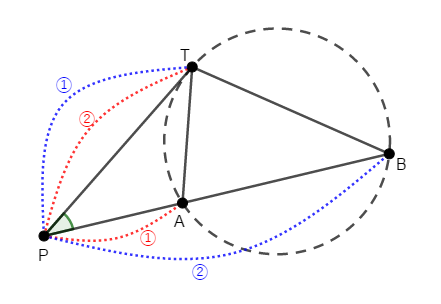
線分\(\mathrm{AB}\)の延長上の点\(\mathrm{P}\)と,直線\(\mathrm{AB}\)上にない点\(\mathrm{T}\)について考える。
このとき,次の式が成り立つならば,直線\(\mathrm{PT}\)は\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{T}\)を通る円の接線である。
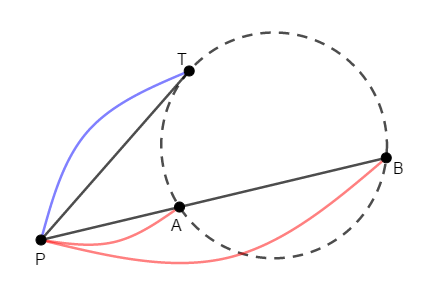
こちらは共円条件ではありません。 そもそも\(3\)点は(共線でなければ)必ず共円です。 それらを頂点とする三角形には,必ず外接円が存在するからです。 この定理は,ある直線がある円の接線であることを示すのに使えます。
では証明を始めましょう。 円の中心が分かりませんから,直線\(\mathrm{PT}\)が\(\mathrm{T}\)を通る円の半径と垂直であることを示すのは難しそうです。 接弦定理の逆を利用しましょう。
まず定理の条件から,次の比の式が成り立ちます。
さらに\(\angle\mathrm{APT} = \angle\mathrm{TPB}\)が共通なので,\(2\)組の辺の比とその間の角が等しいので,\(\triangle\mathrm{APT}\)と\(\triangle\mathrm{TPB}\)が相似であることが分かります。
相似であれば,対応する角が等しいですから,\(\angle\mathrm{PTA} = \angle\mathrm{PBT}\)が成り立ちます。
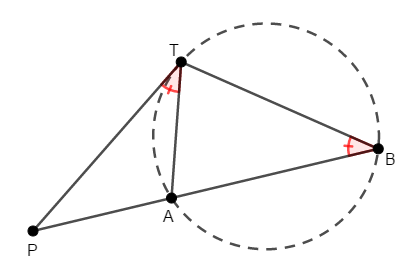
これで弦\(\mathrm{AT}\)に関して\(\mathrm{B}\)と反対側にある点\(\mathrm{P}\)について,\(\angle\mathrm{PTA} = \angle\mathrm{PBT}\)が成り立つため,接弦定理の逆により,直線\(\mathrm{PT}\)は\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{T}\)を通る円の接線です。
方べきの定理の逆の別パターンも証明できましたが,うまく活用できなければ意味がありません。 確認問題にも挑戦しておきましょう。
確認問題
次の問いに答えてください。
-
次の図で\(x\)を求めてください。
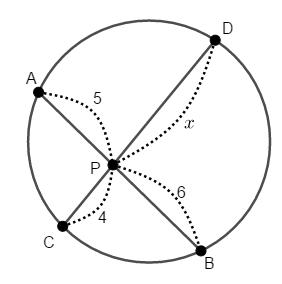
-
次の図で\(y\)を求めてください。
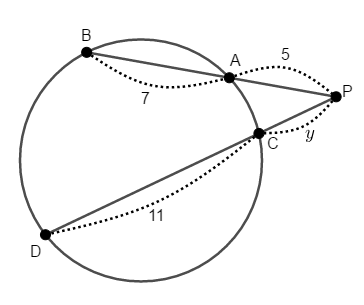
-
次の図で\(z\)を求めてください。 ただし\(\mathrm{T}\)は円の接点です。
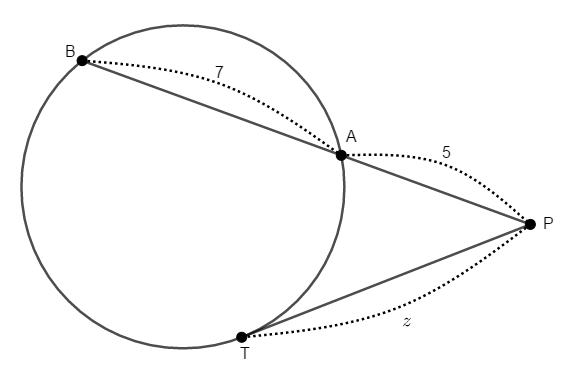
答え
いずれも方べきの定理を使えば解ける問題です。
-
方べきの定理から式を立てられます。
\( \begin{align} \mathrm{PA} \cdot \mathrm{PB} &= \mathrm{PC} \cdot \mathrm{PD} \\[5pt] 5 \cdot 6 &= 4 \cdot x \\[5pt] x &= \displaystyle\frac{15}{2} \end{align} \)したがって,\(x = \displaystyle\frac{15}{2}\)です。
-
方べきの定理から式を立てられます。 \(\mathrm{PA} \cdot \mathrm{AB} = \mathrm{PC} \cdot \mathrm{CD}\)としないように注意してください。
\( \begin{align} \mathrm{PA} \cdot \mathrm{PB} &= \mathrm{PC} \cdot \mathrm{PD} \\[5pt] 5 \cdot (5 + 7) &= y \cdot (y + 11) \\[5pt] y^2 + 11y - 60 &= 0 \\[5pt] (y - 4)(y + 15) &= 0 \end{align} \)したがって,\(y > 0\)に注意すると,\(y = 4\)です。
-
方べきの定理から式を立てられます。 \(\mathrm{PA} \cdot \mathrm{AB} = \mathrm{PT}^2\)としないように注意してください。
\( \begin{align} \mathrm{PA} \cdot \mathrm{PB} &= \mathrm{PT}^2 \\[5pt] 5 \cdot (5 + 7) &= z^2 \\[5pt] z^2 &= 60 \end{align} \)したがって,\(z > 0\)に注意すると,\(z = 2\sqrt{15}\)です。
次の図で,線分\(\mathrm{PS}\),\(\mathrm{PT}\)は円\(\mathrm{O}\)の接線であり,点\(\mathrm{S}\),\(\mathrm{T}\)はその接点です。 この状況で\(\mathrm{OP}\)と\(\mathrm{ST}\)の交点\(\mathrm{H}\)を通る弦\(\mathrm{AB}\)を考えます。
このとき,\(4\)点\(\mathrm{O}\),\(\mathrm{P}\),\(\mathrm{A}\),\(\mathrm{B}\)が共円であることを証明してください。
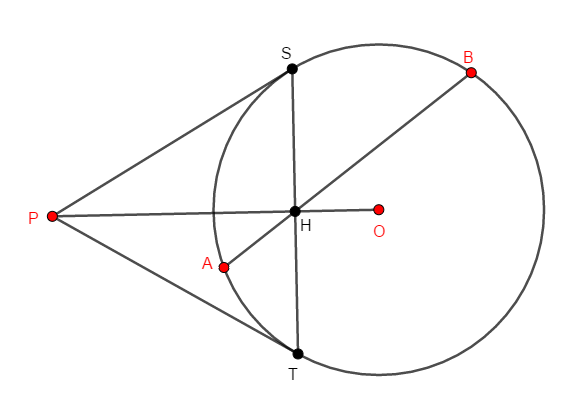
答え
\(4\)点の共円を示す方法はいくつかあります。 円周角の定理の逆を使ったり,\(4\)点を頂点とする四角形の内角が,対角の外角と等しいことを示せば良いです。
ここでは方べきの定理の逆を利用しましょう。 すなわち,次の等式が成り立つことを証明するのを目標にします。
方べきの定理の逆により,次の等式が成り立てば,題意を示せます。
というわけで,この等式を得ることを目標に議論を進めます。
まず目標の式の左辺の形を作ります。 円\(\mathrm{O}\)と弦\(\mathrm{AB}\),\(\mathrm{ST}\)に注目すると,方べきの定理により,次の等式が成り立ちます。
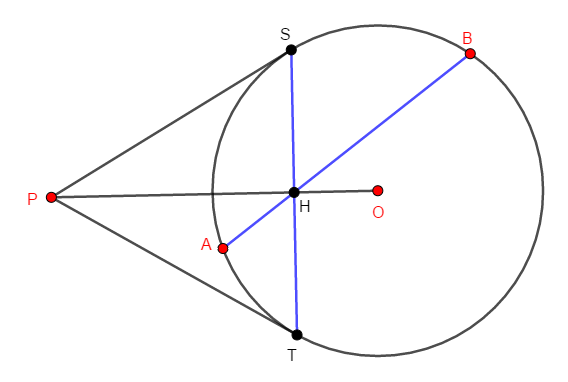
あとはこの右辺を,目標の式の右辺に変形していけば良いです。 ここで\(\mathrm{PS}\),\(\mathrm{PT}\)が円\(\mathrm{O}\)の接線であることに注目すると,\(\angle\mathrm{OSP}\)と\(\angle\mathrm{OTP}\)は直角です。
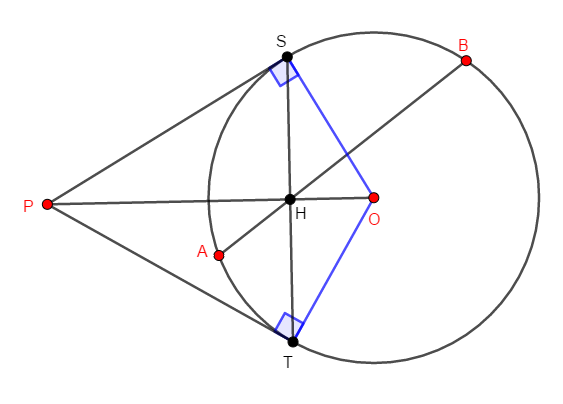
したがって,対角の和が\(180^{\circ}\)であることから,四角形\(\mathrm{OTPS}\)は円に内接します。 この円の弦\(\mathrm{ST}\),\(\mathrm{PO}\)に注目すると,方べきの定理により,次の等式が成り立ちます。
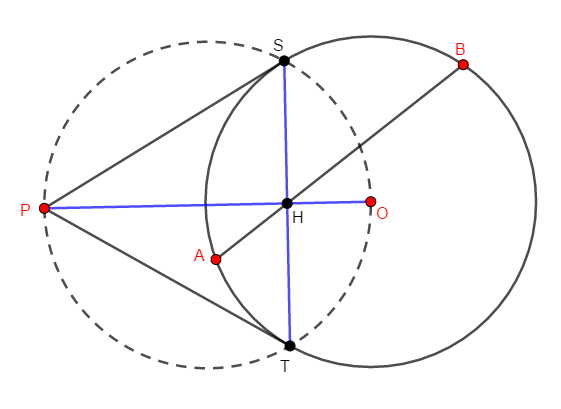
これと先ほど求めた式を組み合わせれば,目標の等式になります。
これで方べきの定理の逆により,\(4\)点\(\mathrm{O}\),\(\mathrm{P}\),\(\mathrm{A}\),\(\mathrm{B}\)が共円であることが証明できました。
