前回までに学んだ円と直線の関係の次は,円と円の関係を考えます。 まずは円と円の位置関係を考えることにしましょう。
目次
2つの円の位置関係
円と直線の位置関係を考えるとき,円の半径\(r\)と,円の中心と直線の距離\(d\)に注目して整理しました。 \(2\)つの円の位置関係も同様に考えてみましょう。
\(2\)つの円の半径を\(R\),\(r\)(\(R > r\)),円の中心間の距離を\(d\)とします。 これらの値を使って,\(2\)つの円の位置関係を考えます。
まずは円が離れている状況を考えます。
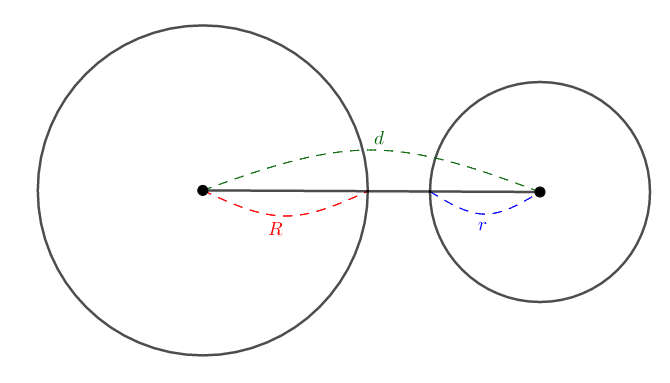
このとき,図を見ての通り,\(d > R + r\)です。 円の半径の和よりも離れているから共有点がないのです。
次にもう少し円同士を近づけると,円同士が接します。
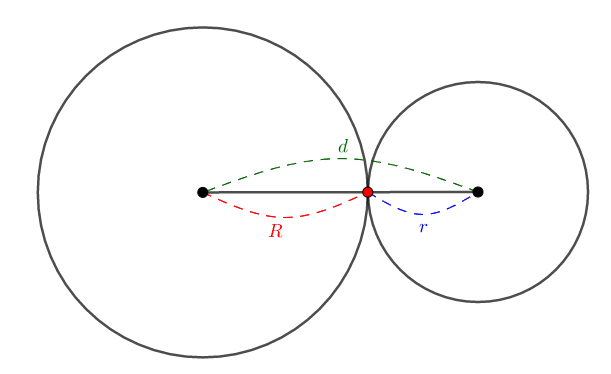
このとき,これらは外接するといいます。 もちろん,この\(1\)つだけある共有点を接点と呼びます。 図を見ての通り,\(d = R + r\)の場合ですね。
もっと円の中心同士を接近させると,共有点は\(2\)つになります。
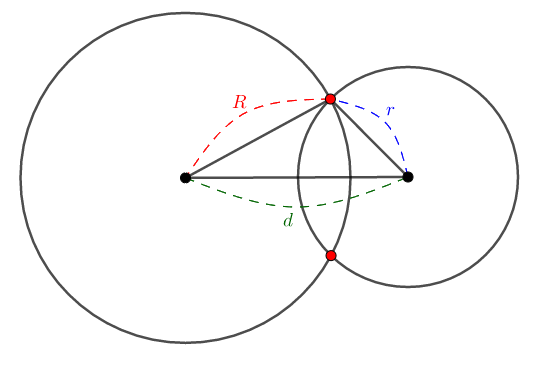
図の通り,このときは各円の半径と中心間の線分により三角形ができます。 三角形の成立条件より,このときは\(R - r < d < R + r\)が成り立ちます。
さらに円の中心間の距離を縮めましょう。 ついに小さい円は大きい円の中に入り込みます。 その最後の瞬間,共有点は\(1\)つだけになります。
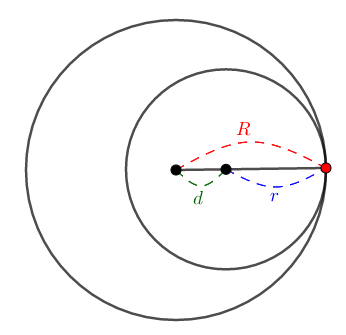
この場合は内接といいます。 円同士の接し方は,外接と内接の\(2\)通りあるのです。
このときは\(R = d + r\)が成り立ちますね。 今まで通り\(d\)を主役にするなら,\(d = R - r\)です。
ここから更に円の中心間の距離を詰めると,ついに小さい円は大きい円の中にすっぽり入ります。
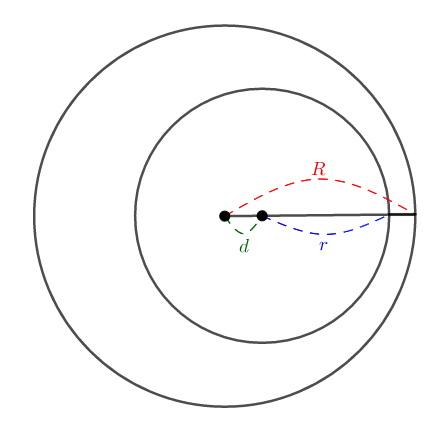
このときは\(R > d + r\)が成り立ちます。 \(d\)を主役にすれば,\(d < R - r\)ですね。
以上をまとめると,円と円の位置関係は,次のように分類できます。
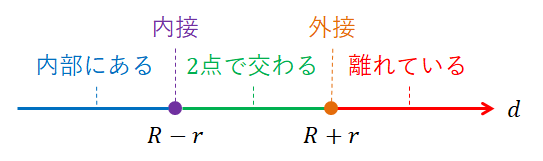
円と円の位置関係は,大きい円の半径を\(R\),小さい円の半径を\(r\),円の中心間の距離を\(d\)とすると,次の\(5\)通りある。
| \(d\)と\(R\)と\(r\)の関係 | 共有点の個数 | 位置関係 |
|---|---|---|
| \(d > R + r\) | \(0\) | 離れている |
| \(d = R + r\) | \(1\) | 外接する |
| \(R - r < d < R + r\) | \(2\) | \(2\)点で交わる |
| \(d = R - r\) | \(1\) | 内接する |
| \(d < R - r\) | \(0\) | 内部にある |
上の議論では,円の半径は異なるものとしていました。 しかし,実際には円の半径が等しい場合もあります。 このときの位置関係はどうなるでしょうか?
これは特に難しい話ではありません。 図を想像すれば分かる通り,「離れている」「外接する」「\(2\)点で交わる」については上の議論と全く同じです。 しかし,「内接する」「内部にある」があり得ないことがすぐ分かるでしょう。
\(d \geqq 0\)であり,\(R - r = 0\)ですから,\(d < R - r\)には決してならないのです。 \(d = R - r\)になることはありますが,これを「内接する」とはいえません。 あえて言えば「一致する」でしょうか。
中心線と共通弦
\(2\)つの円を結び付ける情報として重要なのが,中心線と共通弦です。 中心線とは,\(2\)つの円の中心を通る直線のことです。
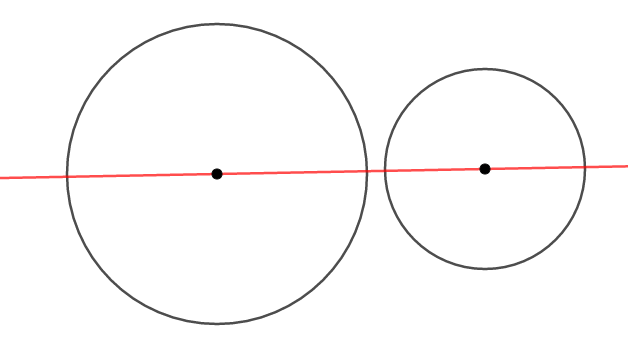
そして共通弦とは,\(2\)つの円が\(2\)点で交わる場合に考えられるもので,\(2\)円に共通する弦です。 弦とは円周上の\(2\)点を結ぶ線分ですから,共通する弦とは\(2\)つの共有点を結んだ線分のことになります。
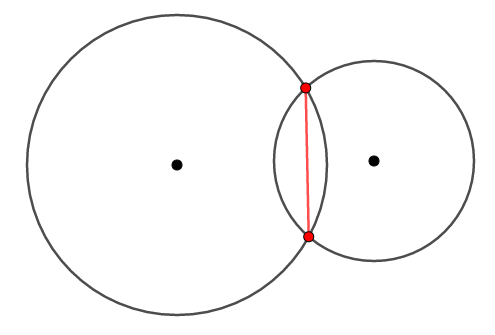
中心線と共通弦について,次の事実が成り立ちます。
中心線は共通弦の垂直二等分線である。
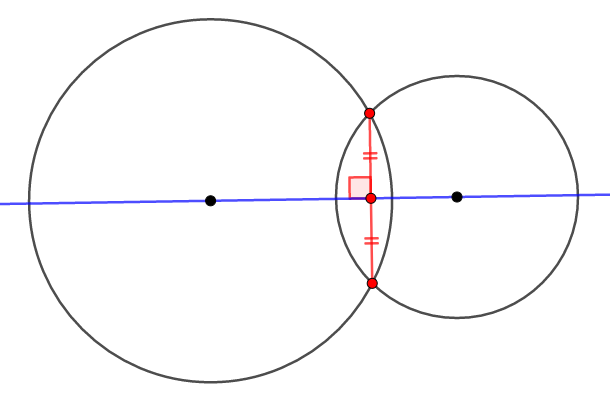
共通弦を考えているので,もちろん\(2\)円が\(2\)点で交わる場合の話です。 図をかくと何となくそうだなあ,と思う内容ですが,証明してみましょう。
\(2\)円の中心をそれぞれ\(\mathrm{O}_1\),\(\mathrm{O}_2\)とし,\(2\)つの共有点を\(\mathrm{A}\),\(\mathrm{B}\)とします。 ここで気付いてほしいのが,\(\triangle\mathrm{O}_1\mathrm{AB}\)と\(\triangle\mathrm{O}_2\mathrm{AB}\)が二等辺三角形であることです。
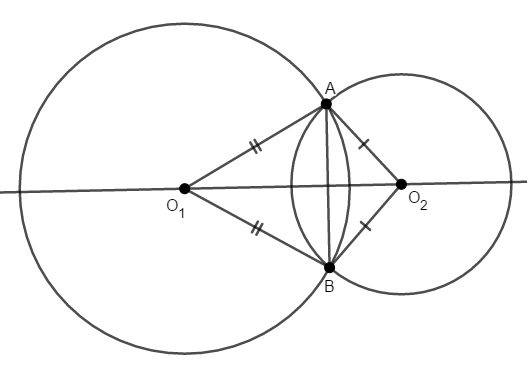
分かるとは思いますが,\(\mathrm{O}_1\mathrm{A}\),\(\mathrm{O}_1\mathrm{B}\)は円\(\mathrm{O}_1\)の半径なので等しく,\(\mathrm{O}_2\mathrm{A}\),\(\mathrm{O}_2\mathrm{B}\)は円\(\mathrm{O}_2\)の半径なので等しいのです。
証明したいのは,中心線がこの二等辺三角形の底辺を垂直に二等分することです。 二等辺三角形の底辺を垂直に二等分するのは,頂角の二等分線でしたね。 だから後は\(\angle\mathrm{AO}_1\mathrm{O}_2 = \angle\mathrm{BO}_1\mathrm{O}_2\)を示せば良いのです。
二等辺三角形の頂角の二等分線は,底辺を垂直に\(2\)等分する。 以外と忘れがちかもしれません。 底角が等しいという性質と比べると,確かに難しいかもしれません。
忘れている場合は,こちらで復習しておきましょう。
さて,\(\angle\mathrm{AO}_1\mathrm{O}_2 = \angle\mathrm{BO}_1\mathrm{O}_2\)を示すのは簡単です。 図を見てすぐ気付く通り,\(\triangle\mathrm{AO}_1\mathrm{O}_2\)と\(\triangle\mathrm{BO}_1\mathrm{O}_2\)は合同です。 \(\mathrm{O}_1\mathrm{A} = \mathrm{O}_1\mathrm{B}\),\(\mathrm{O}_2\mathrm{A} = \mathrm{O}_2\mathrm{B}\)であり,\(\mathrm{O}_1\mathrm{O}_2\)が共通ですから,\(3\)辺がそれぞれ等しいですね。
合同であれば対応する角が等しいので,\(\angle\mathrm{AO}_1\mathrm{O}_2 = \angle\mathrm{BO}_1\mathrm{O}_2\)です。 これで中心線\(\mathrm{O}_1\mathrm{O}_2\)が二等辺三角形\(\triangle\mathrm{O}_1\mathrm{AB}\)の頂角の二等分線であり,底辺である共通弦\(\mathrm{AB}\)を垂直に\(2\)等分することが分かりました。
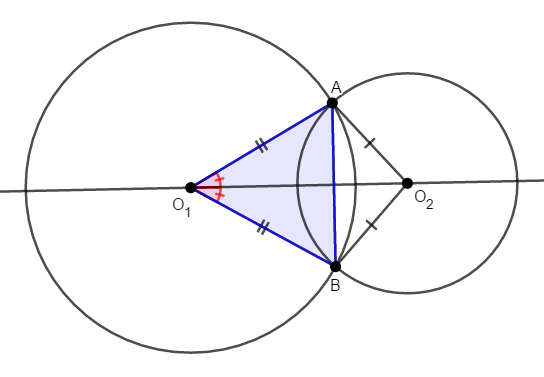
中心線に関して,もうひとつ性質を見てみます。 先ほどは\(2\)つの円が\(2\)点で交わる場合を考えましたが,次は接する場合を考えます。
円同士の接し方には,外接と内接がありますが,どちらにしてもその接点は,中心線上にあります。
接点は中心線上にある。
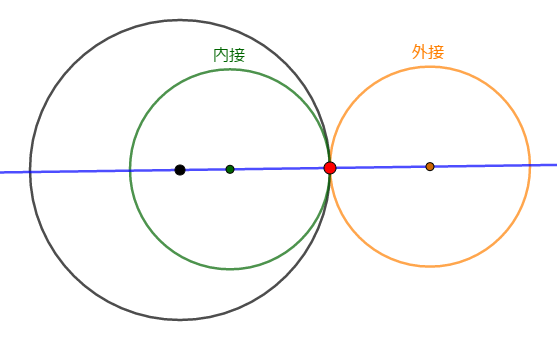
直感的にも正しそうな内容ですが,証明も簡単です。 上図を見てください。 \(2\)つの円は,中心線に関して対称ですね。
もし接点が中心線上になければ,中心線に関してそれと対称な位置にもうひとつ共有点があることになり,接することに矛盾します。 だから接点は中心線上にしかありえないのです。
これらの事実が自然なことと思えるようにしておきましょう。
確認問題
半径\(3\)の円\(\mathrm{O}_1\)と半径\(7\)の円\(\mathrm{O}_2\)があります。 これらの円が接するとき,線分\(\mathrm{O}_1\mathrm{O}_2\)の長さを求めてください。
答え
円と円の接し方には,外接と内接があることに注意してください。 答えは\(2\)通りあるわけです。
外接・内接両方の場合を同じ図に書き込むと,次のようになります。 円\(\mathrm{O}_1\)の方が小さいですから,内接の場合は円\(\mathrm{O}_2\)の中に円\(\mathrm{O}_1\)が入る形になります。
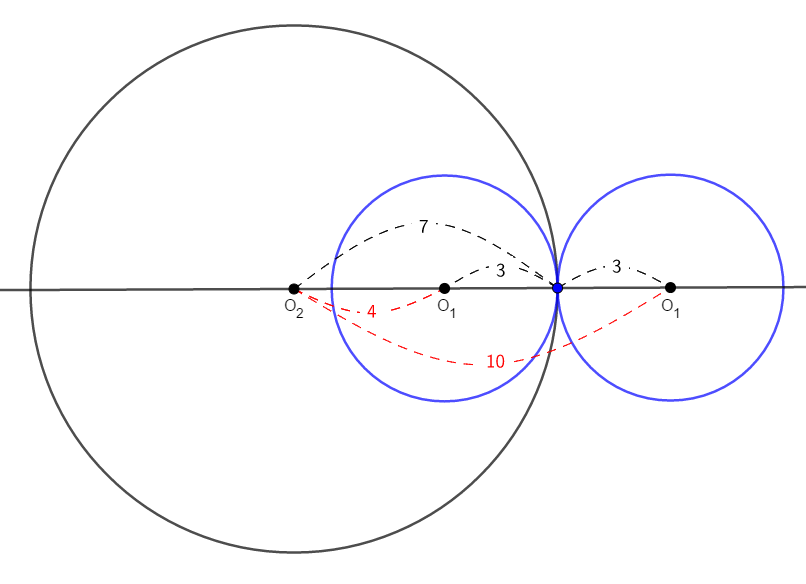
図を見れば,外接の場合は\(\mathrm{O}_1\mathrm{O}_2 = 10\),内接の場合は\(\mathrm{O}_1\mathrm{O}_2 = 4\)であることが分かります。 接点が中心線上にありますから,単純な半径の足し引きで計算できるわけです。
本文の内容を覚えていれば,外接の場合は半径の和,内接の場合は半径の差を計算するだけでも分かりますね。
半径\(8\)の円\(\mathrm{O}_1\)と半径\(6\)の円\(\mathrm{O}_2\)が,\(\mathrm{O}_1\mathrm{O}_2 = 4\)の距離で配置されています。 これらの円の共通弦の長さを求めてください。
答え
まずは図をかきましょう。 \(2\)つの円の共有点を\(\mathrm{A}\),\(\mathrm{B}\)とすると,求めたいのは\(\mathrm{AB}\)の長さですね。
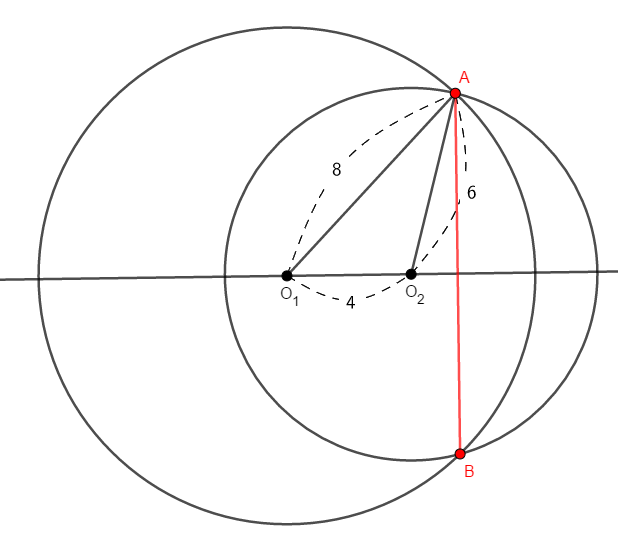
中心線は共通弦を垂直に\(2\)等分するので,中心線と共通弦の交点を\(\mathrm{H}\)とし,まずは\(\mathrm{AH}\)を求めることにしましょう。
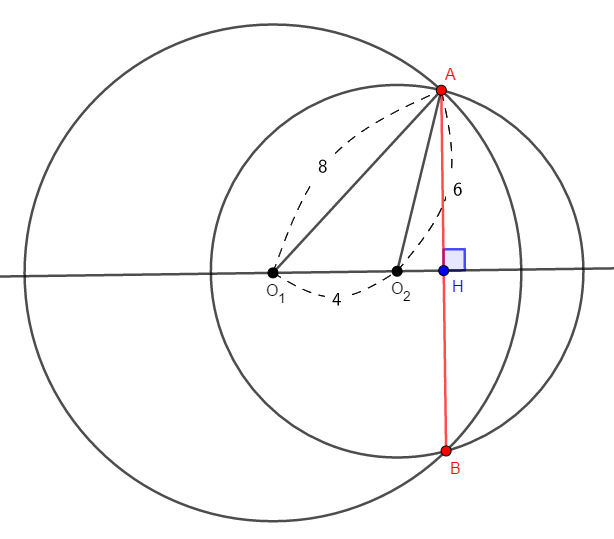
直角三角形\(\triangle\mathrm{AHO}_1\)と\(\triangle\mathrm{AHO}_2\)ができましたが,それぞれ\(\mathrm{HO}_1\),\(\mathrm{HO}_2\)の長さが分からないので,三平方の定理から一発で\(\mathrm{AH}\)を求めることはできません。
しかし直角三角形が\(2\)つあるということは,三平方の定理から\(2\)つの方程式を立てられるということですから,未知数が\(2\)つあっても大丈夫です。 \(\mathrm{AH} = x\),\(\mathrm{HO}_2 = y\)とし,これらを両方とも求めてしまいましょう。
必要な図だけ抜き出すと,次の通りです。
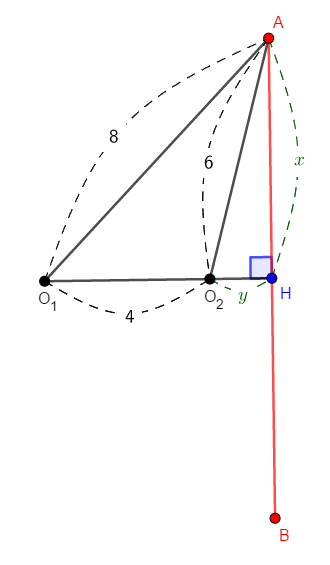
直角三角形\(\triangle\mathrm{AHO}_1\),\(\triangle\mathrm{AHO}_2\)のそれぞれについて,三平方の定理から方程式を立てます。
式を少し整理します。
上の式から下の式を辺々引けば,次のように\(y\)が求められます。
次はこの\(y\)を使って,\(x\)を求めます。 \(x > 0\)であることに注意し,\(x^2 + y^2 = 36\)に代入して計算しましょう。
共通弦の長さは\(\mathrm{AB} = 2\mathrm{AH} = 2x\)ですから,その値は\(3\sqrt{15}\)です。
