前回,円と円を結び付ける情報として中心線と共通弦を学びました。 今回は,それに加えて共通接線を考えます。
目次
2つの円の共通接線
今回は\(2\)つの円に共通する接線(共通接線)を考えてみます。 どんな風に接線が引けるかは,もちろん円と円の位置関係によって変わります。
円と円の位置関係については,前回学びました。 「離れている」「外接する」「\(2\)点で交わる」「内接する」「内部にある」の\(5\)通りがありましたね。 それぞれの場合について,共通接線を考えていきます。
まずは円と円が離れている場合です。 このとき,次のように\(4\)本の共通接線が引けます。
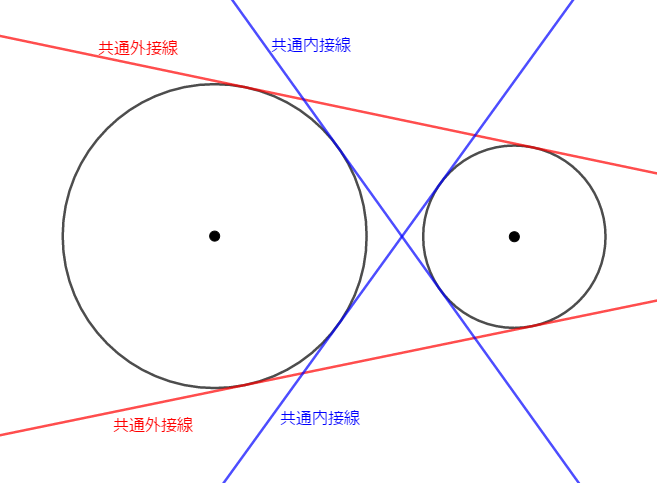
図の赤線のように円と円の間を通らない接線を共通外接線,青線のように円と円の間を通る接線を共通内接線といいます。 ちゃんと言い直すと,\(2\)円が接線に関して同じ側にあるとき共通外接線,反対側にあるとき共通内接線です。
円の外部の点から円に接線を引くとき,接線の長さというものを考えました。 共通接線についても,その長さを考えることがよくあります。 共通接線の長さとは,各円での接点間の距離です。
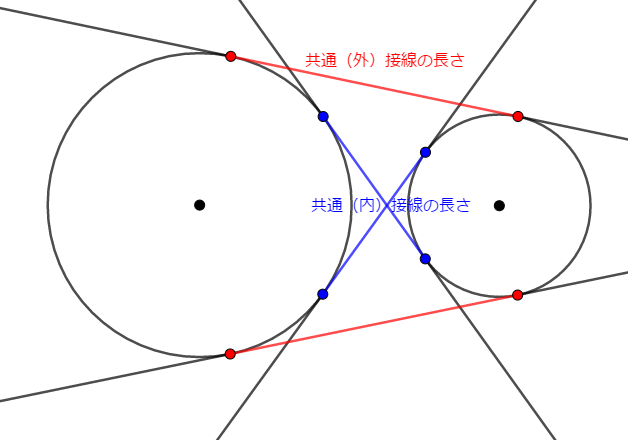
円と円が離れている場合の共通接線については分かりました。 次は外接する場合を考えてみると,次のように\(3\)本の共通接線が引きます。
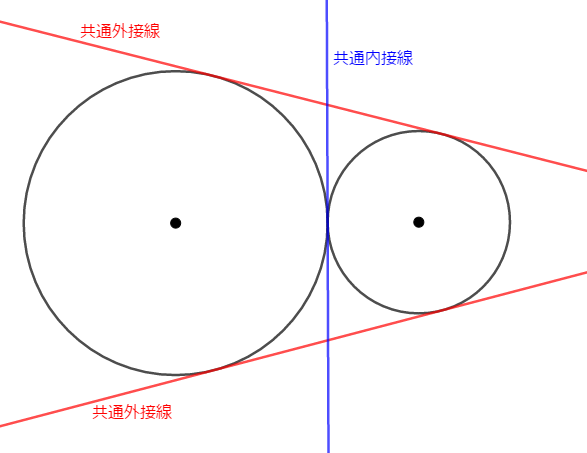
かろうじて「円と円の間」が存在するので,共通内接線は\(1\)本だけ引けます。 その接点は,円と円の接点と一致します。 共通外接線は変わらず\(2\)本引けますね。
次は円と円が\(2\)点で交わる場合を考えましょう。 このときの共通接線は,次のように\(2\)本だけ引けます。
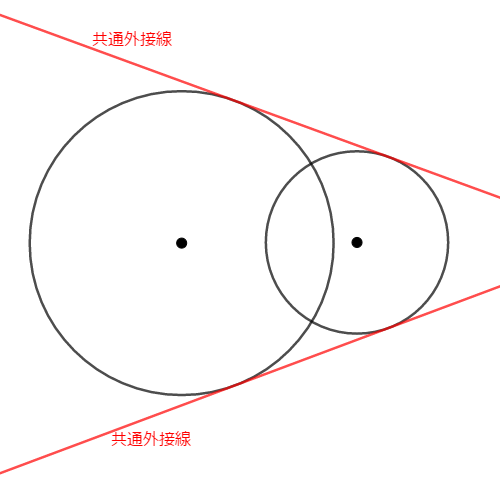
ついに「円と円の間」が消滅したので,共通内接線は引けなくなりました。 共通外接線であれば,変わらず\(2\)本引けます。
次に考えるのは,内接する場合です。 もう共通接線は\(1\)本しか引けません。
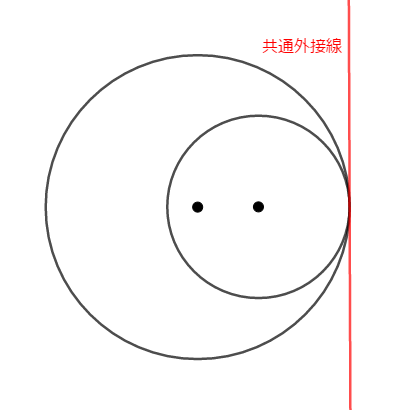
共通内接線は当然引けません。 共通外接線も\(1\)本しか引けなくなりました。 その接点は,円と円の接点と一致します。
最後に円が円の内部にある場合を考えますが,もはや共通接線を引くことはできません。
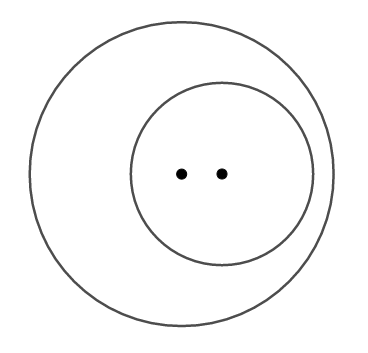
これで円と円の位置関係ごとに,どのような共通接線が引けるか,一通り確認できました。
円と円の共通接線の本数は,円と円の位置関係によって次のように決まる。
| 位置関係 | 共通接線数 |
|---|---|
| 離れている | \(4\) |
| 外接する | \(3\) |
| \(2\)点で交わる | \(2\) |
| 内接する | \(1\) |
| 内部にある | \(0\) |
円同士が近づくにつれて,共通接線の本数が減っていますね。 まず「円と円の間」がなくなることで共通内接線が引けなくなり,最後には大円が小円を取り込むことで,共通外接線すら引けなくなるわけです。
共通接線に関する問題としては,その長さを問うものなどが多いです。 確認問題をしっかり解けるようにしておきましょう。
確認問題
半径\(3\)の円\(\mathrm{O}_1\)と半径\(2\)の円\(\mathrm{O}_2\)が,\(\mathrm{O}_1\mathrm{O}_2 = 6\)の距離で配置されています。 これらの円の共通外接線・共通内接線の長さを求めてください。
答え
この場合,円同士は離れていますから,共通外接線・共通内接線はそれぞれ\(2\)本ずつ引けます。 しかし,図の対称性から共通外接線同士,共通内接線同士の長さはそれぞれ等しいので,考えるのは\(1\)本ずつでOKです。
まずは共通外接線の長さを求めましょう。 共通外接線と円\(\mathrm{O}_1\),\(\mathrm{O}_2\)の交点をそれぞれ\(\mathrm{A}\),\(\mathrm{B}\)とすると,問題の状況は次図のようになります。
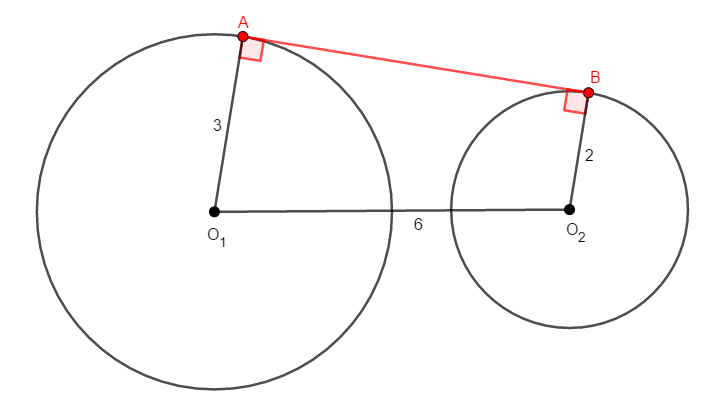
ここで,円の接線は,その接点を通る半径に垂直であることに注意してください。 \(\angle\mathrm{A}\)と\(\angle\mathrm{B}\)が直角であることから,\(\mathrm{O}_1\mathrm{A}\)と\(\mathrm{O}_2\mathrm{B}\)が平行であることが分かります。
詳しくかけば,\(\angle\mathrm{A}\)の外角と\(\angle\mathrm{B}\)が等しいことから,同位角(または錯角)が等しいことが分かるので,\(\mathrm{O}_1\mathrm{A}\)と\(\mathrm{O}_2\mathrm{B}\)は平行なのです。
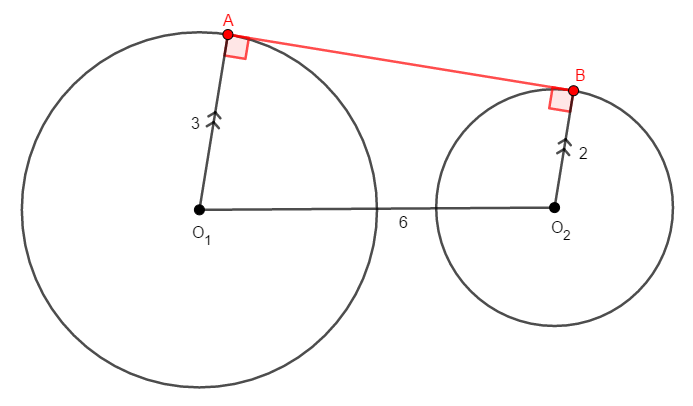
これで図の状況は大体分かりました。 しかし,\(\mathrm{AB}\)がまだ求められません。 そこで,\(\mathrm{AB}\)を移動することを考えましょう。
線分の移動も角の移動も,基本は平行線を引くことから始まります。 \(\mathrm{AB}\)と平行で\(\mathrm{O}_2\)を通る直線と\(\mathrm{O}_1\mathrm{A}\)の交点を\(\mathrm{P}\)としましょう。
このとき,平行であれば同位角や錯角が等しいことから,四角形\(\mathrm{BAPO}_2\)の内角は全て直角であり,長方形ですから,\(\mathrm{AB} = \mathrm{PO}_2\)であることが分かります。
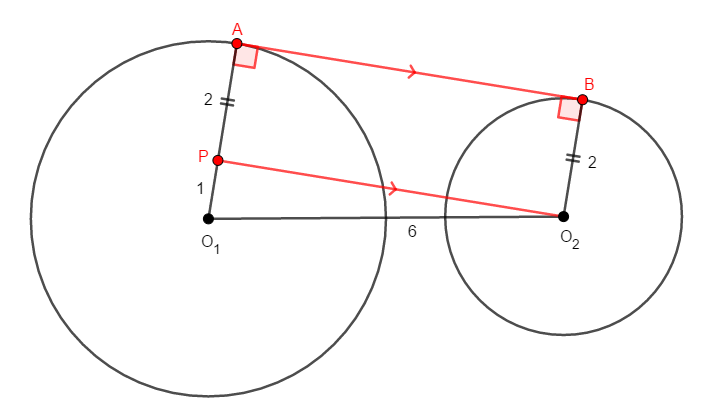
ここで\(\triangle\mathrm{PO}_1\mathrm{O}_2\)に注目しましょう。 \(\angle\mathrm{P}\)は直角ですから,これは直角三角形です。 さらに\(\mathrm{AP} = \mathrm{BO}_2 = 2\)から,\(\mathrm{PO}_1 = 1\)であることが分かります。
したがって,三平方の定理より,\(\mathrm{PO}_2\)が求められます。
次に共通内接線の長さを求めます。 共通内接線と円\(\mathrm{O}_1\),\(\mathrm{O}_2\)の交点をそれぞれ\(\mathrm{C}\),\(\mathrm{D}\)とすると,問題の状況は次図のようになります。
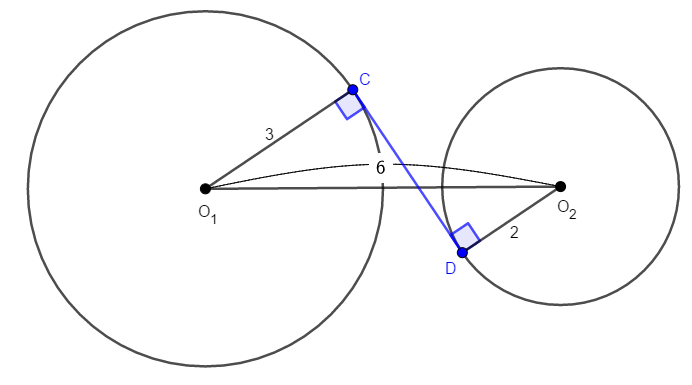
議論は共通外接線の場合とほぼ同じです。 円の接線は,その接点を通る円の半径に垂直ですから,\(\angle\mathrm{C}\),\(\angle\mathrm{D}\)は直角であり,錯角が等しいことから,\(\mathrm{CO}_1\)と\(\mathrm{DO}_2\)が平行であることが分かります。
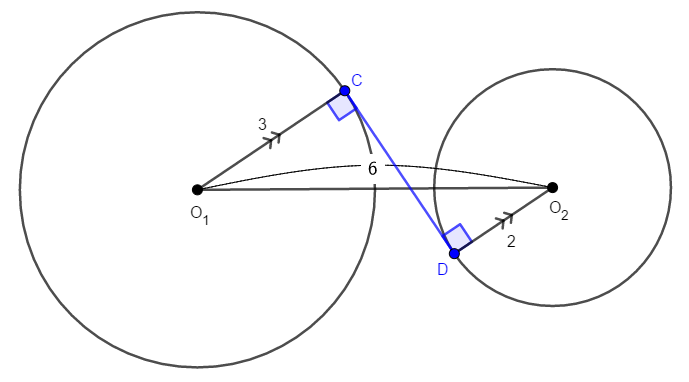
次に\(\mathrm{CD}\)を求めるために,この線分の移動を考えます。 \(\mathrm{CD}\)と平行で\(\mathrm{O}_1\)を通る直線と\(\mathrm{O}_2\mathrm{D}\)の延長の交点を\(\mathrm{Q}\)とします。
このとき,四角形\(\mathrm{CDQO}_1\)は内角がすべて直角であり,長方形ですから,\(\mathrm{CD} = \mathrm{QO}_1\),\(\mathrm{QD} = \mathrm{CO}_1 = 3\)です。
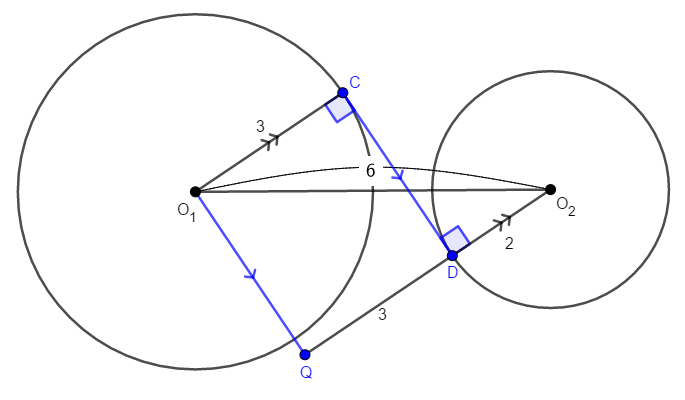
ここで\(\triangle\mathrm{QO}_1\mathrm{O}_2\)に注目すると,\(\angle\mathrm{Q}\)は直角ですから,これは直角三角形です。 したがって,三平方の定理より,\(\mathrm{QO}_1\)が求められます。
以上から,共通外接線の長さは\(\sqrt{35}\),共通内接線の長さは\(\sqrt{11}\)です。
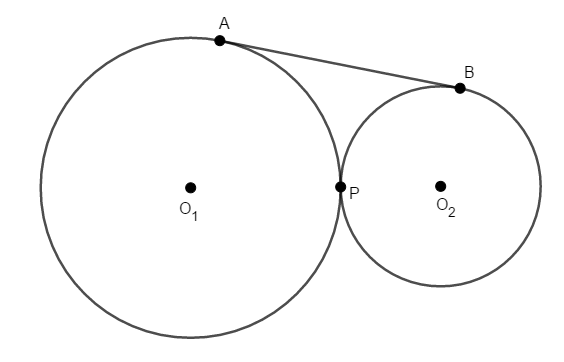
点\(\mathrm{P}\)で外接する円\(\mathrm{O}_1\),\(\mathrm{O}_2\)に共通外接線を引き,それぞれの円との接点を\(\mathrm{A}\),\(\mathrm{B}\)とします。
このとき,\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{P}\)を通る円の中心の位置を求めてください。
答え
求める点は,\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{P}\)と等距離にある点です。 作図するなら,\(\triangle\mathrm{ABP}\)の各辺の垂直二等分線の交点を求めれば良いですね。 しかし,その位置が具体的にどこなのかを知るには,もう少し考える必要があります。
ここで「接点」「接線」「等距離」というキーワードから,思い出すべきことがあります。 円の外部の点から引いた\(2\)本の接線の長さは等しいということです。
いま,各円の接線は共通外接線の\(1\)本しかありません。 もう\(1\)本の接線として,共通内接線も引き,\(\mathrm{AB}\)との交点を\(\mathrm{X}\)としましょう。
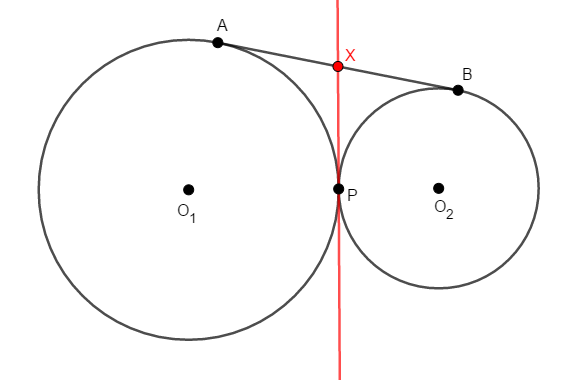
外接する円の共通内接線は,円同士の接点\(\mathrm{P}\)を通ることに注意してください。
さて,先ほど確認した通り,円の外部の点からその円に引いた接線の長さは等しいです。 円の外部の点として\(\mathrm{X}\)を考えれば,次の等式が成り立つことが分かります。
\(1\)行目は円\(\mathrm{O}_1\)に引いた接線の長さについて,\(2\)行目は円\(\mathrm{O}_2\)に引いた接線の長さについての等式です。
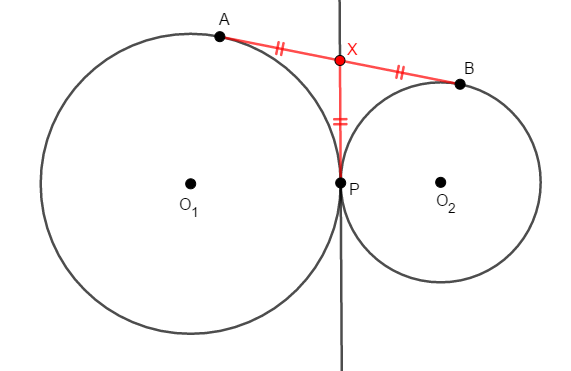
したがって,\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{P}\)と等距離にある点が\(\mathrm{X}\)であることが分かりました。 さらに,この点が線分\(\mathrm{AB}\)の中点であることも分かります。
以上から,求める円の中心は,線分\(\mathrm{AB}\)の中点にあります。
