前回までで数学Aの平面図形を一通り学びました。 ここで平面図形の証明問題を解くうえで必要な「証明道具」をまとめておきましょう。
また,高校数学でも中学で学んだ「証明道具」が必要になります。 中学の「証明道具」については,こちらで復習できます。
目次
共点の証明
いくつかの直線が\(1\)点で交わるとき,それらの直線を共点であるというのでした。 \(3\)本の直線が共点であることを示す方法を確認しましょう。
共点を示すには,共点であるための条件,すなわち共点条件を把握しておく必要があります。 代表的な共点条件は\(3\)つあり,\(2\)つは中学レベルです。
\(3\)直線が次のいずれかを満たすとき,それらは共点である。
① \(2\)直線の交点をもう\(1\)つの直線が通る。
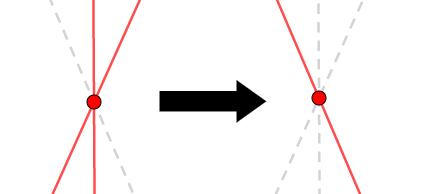
② \(2\)直線ずつの交点が一致する。
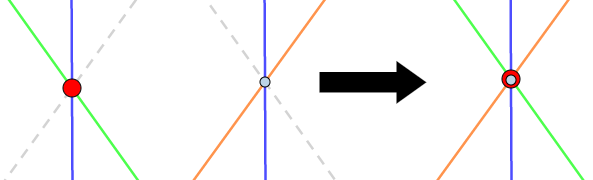
これらの発想は,\(3\)本の直線を同時に扱うことはせず,\(2\)つずつのペアで考えるというものです。 ①は「直線・直線ペア → 交点・直線ペア」,②は「直線・直線ペア → 交点・交点ペア」で考えます。
角や辺の二等分線のように,直線の性質などがはっきりしている場合,この共点条件が使いやすいです。 \(2\)直線の交点が,両直線の性質を併せ持つことに注目します。
これらに加えて,数学Aで新たに学んだ共点条件がチェバの定理の逆です。
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)とその延長上にそれぞれ点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)があるとする。 これが次の【条件】を全て満たすとき,\(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)は共点である。(\(1\)点で交わる。)
【条件】
① \(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)のうち,\(\triangle\mathrm{ABC}\)の辺上にあるのは,\(1\)点または\(3\)点である。
② \(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)のうち,\(2\)本が交わる。
③ 次の式が成り立つ。
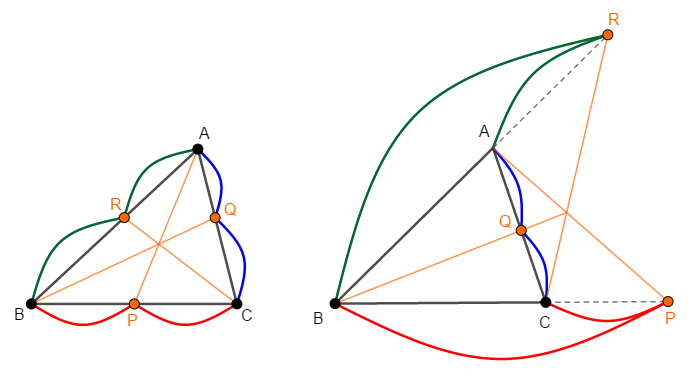
いつ見てもややこしいのですが,大事なのは図の状況を頭に入れることです。 この図の状況を言葉で説明すると複雑になるのですが,図の状況はそこまで難しくはありません。
線分の比をとるので,各線分の長さやその比が分かっている場合に便利な定理です。 線分の比は三角形の相似を考えたり,面積比を考えることで得られる場合が多いです。
ちなみに,\(3\)点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が三角形の辺上にある場合に限定すれば,この定理の内容を簡単に表せます。 条件①,②を明らかに満たすので,条件③だけで済むのです。
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)上にそれぞれある点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)を考える。
これが次の式を満たすとき,\(\mathrm{AP}\),\(\mathrm{BQ}\),\(\mathrm{CR}\)は共点である。
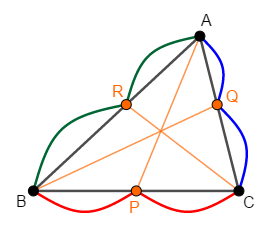
先ほどの完全版と比べて,この簡易版は一般性が失われますが,圧倒的に覚えやすいです。 少なくともこちらは覚えておきましょう。
共線の証明
いくつかの点が一直線上にあるとき,それらの点を共線であるというのでした。 \(3\)点が共線であることを示す方法を確認しましょう。
共線を示すには,共線であるための条件,すなわち共線条件を把握しておく必要があります。 代表的な共線条件は\(4\)つあり,\(3\)つは中学レベルです。
\(3\)点が次のいずれかを満たすとき,それらは共線である。
① \(2\)点を結ぶ直線上にもう\(1\)つの点がある。
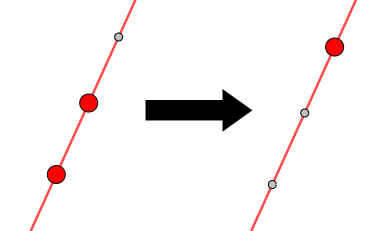
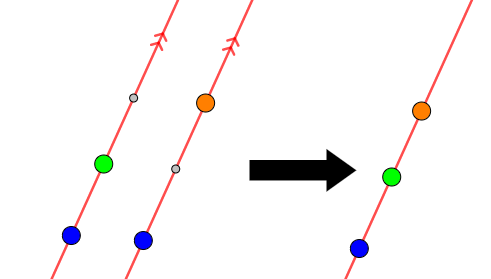
② \(2\)点ずつを結んでできる\(2\)直線が平行である。
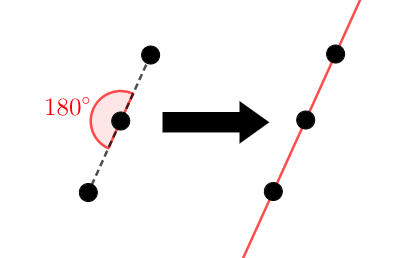
③ \(3\)点のなす角が\(180^{\circ}\)である。
①と②は,共点条件と同じく,\(3\)点を同時は考えず,\(2\)つずつのペアで考えるものです。 ②は\(2\)点ずつで作った直線が一致することを示すための条件ですが,これらは少なくとも\(1\)点を共有しているので,平行でさえあれば一致するのです。
③は共線条件ならではで,使いやすいです。 \(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)がこの順で並ぶとき,\(\mathrm{B}\)の周りの角度を考えれば良いですね。
これらに加えて,数学Aで新たに学んだ共線条件がメネラウスの定理の逆です。
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)とその延長上にそれぞれ頂点でない点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)があるとする。 これが次の【条件】を全て満たすとき,\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)は共線である。(同一直線上にある。)
【条件】
① \(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)のうち,\(\triangle\mathrm{ABC}\)の辺上にあるのは,\(0\)点または\(2\)点である。
② 次の式が成り立つ。
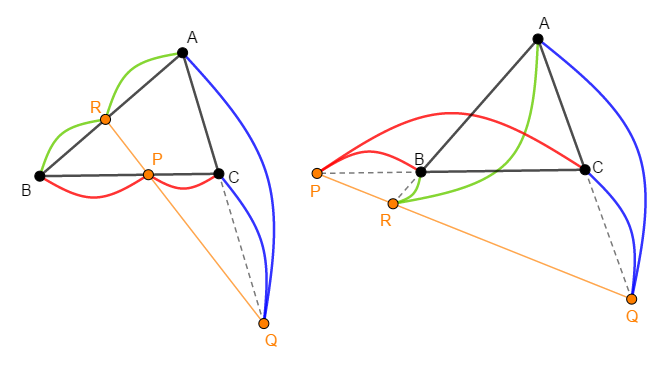
ややこしいのですが,チェバの定理の逆よりはシンプルです。 こちらも,図の状況を頭に入れておくことが重要です。 これを言葉にするからややこしいのです。
線分の比をとるので,各線分の長さやその比が分かっている場合に便利な定理です。 チェバの定理の逆と同様ですね。
共円の証明
いくつかの点が同一円周上にあるとき,それらの点を共円であるというのでした。 \(4\)点が共円であることを示す方法を確認しましょう。
(ちなみに,三角形には必ず外接円が存在することから,共線でない\(3\)点は必ず共円です。)
共円を示すには,共円であるための条件,すなわち共円条件を把握しておく必要があります。 代表的な共円条件は\(3\)つあり,\(1\)つは中学レベルです。
\(2\)点\(\mathrm{X}\),\(\mathrm{Y}\)が直線\(\mathrm{AB}\)に対して同じ側にあり,次が成り立つとき,\(4\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{X}\),\(\mathrm{Y}\)は共円である。 (同一円周上にある。)
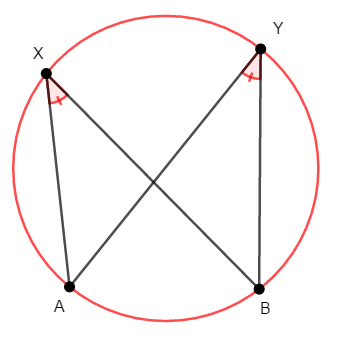
これは言葉だけ見ると難しそうですが,要は円周角に相当する角が等しければOKという話です。 円周角の定理はよく使いますから,頭に残りやすいでしょう。
これに加えて,数学Aで新たに学んだ共円条件を確認しましょう。 まずは四角形が円に内接する条件です。
次のいずれかが成り立つ四角形は,円に内接する。 (その\(4\)頂点は共円である。)
- 対角の和が\(180^{\circ}\)である。
- 内角とその対角の外角が等しい。
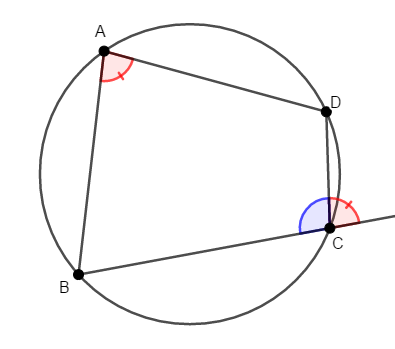
共円を示す問題では,この定理の出番が多いです。 線分の長さやその比と比べると,角度の情報は得やすいからです。
もうひとつ数学Aで新たに学んだのは,方べきの定理の逆です。
\(2\)つの線分\(\mathrm{AB}\),\(\mathrm{CD}\)またはその延長の交点を\(\mathrm{P}\)とする。
このとき,次の式が成り立つならば,\(4\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\),\(\mathrm{D}\)は共円である。 (同一円周上にある。)
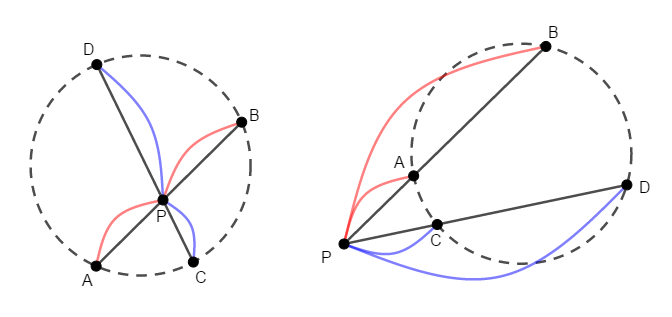
こちらは角度の情報を使わず,線分の長さやその比の情報を使います。 そのような情報が揃うときには,この定理を使いましょう。
接線の証明
最後に,ある直線が,ある円の接線であることを示す方法を確認しましょう。 代表的な方法は\(3\)つあり,\(1\)つは中学レベルです。
円周上の点を通る直線が,その点を通る半径に垂直であるとき,この直線はこの円の接線である。
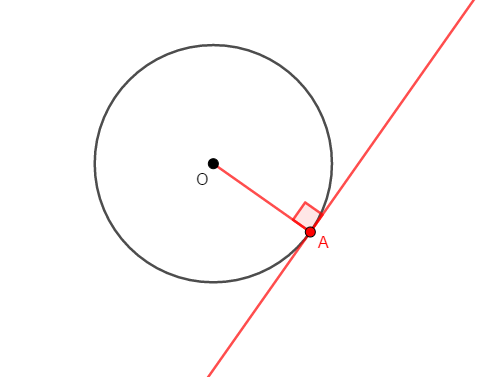
この定理の逆の「円の接線はその接点を通る半径に垂直」も重要です。 あわせて使いこなせるようにしましょう。
これに加えて,数学Aで新たに学んだ定理を確認しましょう。 まずは接弦定理の逆です。
円\(\mathrm{O}\)の円周上に\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)がある状況を考える。
点\(\mathrm{A}\)を通る直線上の,弦\(\mathrm{AB}\)に関して\(\mathrm{C}\)と反対側に点\(\mathrm{X}\)をとり,次の等式が成り立つとき,この直線は円\(\mathrm{O}\)の接線である。
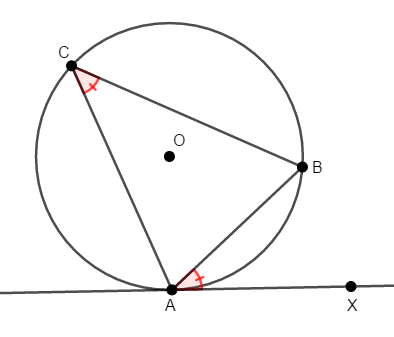
これも定理の内容だけ見るとややこしいです。 図形を文字だけで表現するので,無理もありません。 やはり図の状況を頭に入れることが重要で,そもそも接弦定理が重要な定理ですから,必ずこの図を頭に入れてください。
この定理は角度の情報によって,接線であることを示すものです。 角度の情報が多く得られる場合に使えます。
もうひとつ数学Aで新たに学んだのは,方べきの定理の逆です。 共円条件でも出てきましたが,接線の証明にも使えるバージョンがあります。
線分\(\mathrm{AB}\)の延長上の点\(\mathrm{P}\)と,直線\(\mathrm{AB}\)上にない点\(\mathrm{T}\)について考える。
このとき,次の式が成り立つならば,直線\(\mathrm{PT}\)は\(3\)点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{T}\)を通る円の接線である。
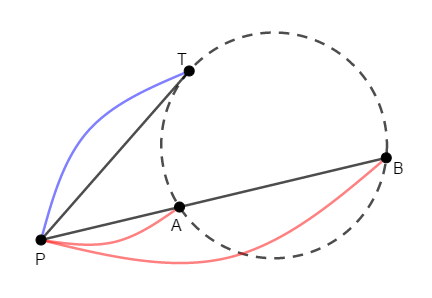
こちらは角度の情報を使わず,線分の長さやその比の情報を使います。 そのような情報が揃うときが,使いどころです。
各定理の「条件」を理解していれば,いつどの定理が使えそうか分かります。 角度の情報を使うもの,線分の長さの情報を使うものなど,各定理の使いどきを心得ておきましょう。
確認問題
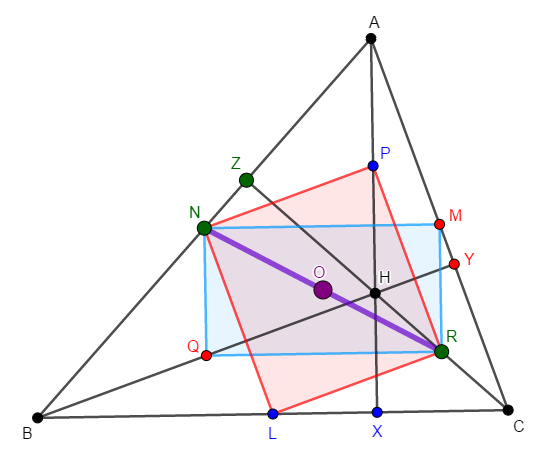
そんなに難しくはありませんが,平面図形の集大成感のある,すごそうな定理を証明しましょう。 九点円というものについてです。
\(\triangle\mathrm{ABC}\)について,次のように色々な点をとります。
① 各頂点から対辺に垂線\(\mathrm{AX}\),\(\mathrm{BY}\),\(\mathrm{CZ}\)を下ろし,垂心\(\mathrm{H}\)をとる。
② 各辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)の中点をそれぞれ\(\mathrm{L}\),\(\mathrm{M}\),\(\mathrm{N}\)とする。
③ 線分\(\mathrm{AH}\),\(\mathrm{BH}\),\(\mathrm{CH}\)の中点をそれぞれ\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)とする。
このとき,\(9\)点\(\mathrm{X}\),\(\mathrm{Y}\),\(\mathrm{Z}\),\(\mathrm{L}\),\(\mathrm{M}\),\(\mathrm{N}\),\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が共円であることを証明しましょう。
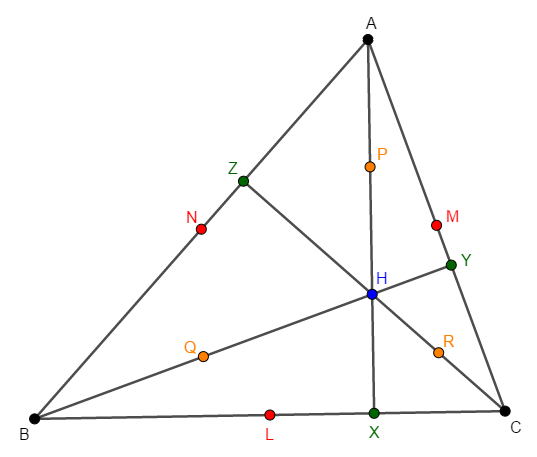
簡単のため,\(\triangle\mathrm{ABC}\)は鋭角三角形とし,上図の状況で考えます。 次の問いに答えてください。
-
四角形\(\mathrm{NMRQ}\)が平行四辺形であることを証明してください。
-
四角形\(\mathrm{NMRQ}\)が長方形であることを証明してください。
-
\(6\)点\(\mathrm{N}\),\(\mathrm{M}\),\(\mathrm{R}\),\(\mathrm{Q}\),\(\mathrm{Y}\),\(\mathrm{Z}\)が共円であることを証明してください。
-
\(9\)点\(\mathrm{X}\),\(\mathrm{Y}\),\(\mathrm{Z}\),\(\mathrm{L}\),\(\mathrm{M}\),\(\mathrm{N}\),\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)が共円であることを証明してください。
答え
\(9\)点の共円を証明するのは大変そうですが,小問を順に解いていけば難しくはありません。 ただ情報量が多いので,うまく図形を抜き出して整理する必要があります。
-
\(\mathrm{N}\),\(\mathrm{M}\),\(\mathrm{R}\),\(\mathrm{Q}\)は,どれもある線分の中点です。 三角形と中点があるときは,中点連結定理チャンスです。
まず\(\triangle\mathrm{ABC}\)に注目しましょう。 中点連結定理より,次が成り立ちます。
\( \begin{align} &\mathrm{BC} = 2\mathrm{NM} \\[5pt] &\mathrm{BC} /\!/ \mathrm{NM} \end{align} \)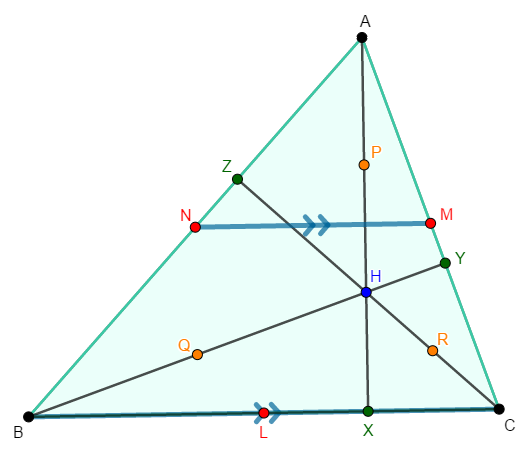
次に\(\triangle\mathrm{HBC}\)に注目しましょう。 中点連結定理より,次が成り立ちます。
\( \begin{align} &\mathrm{BC} = 2\mathrm{QR} \\[5pt] &\mathrm{BC} /\!/ \mathrm{QR} \end{align} \)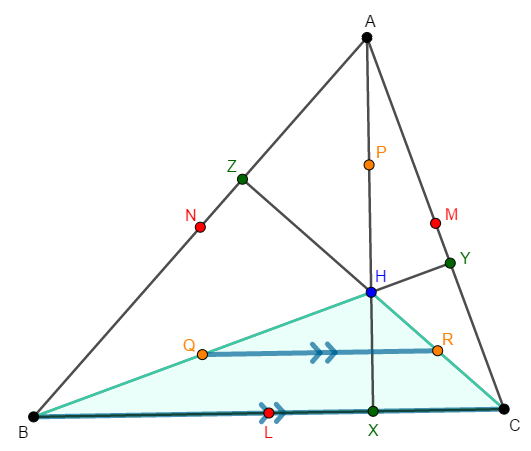
以上から,次が成り立ちます。
\( \begin{align} &\mathrm{NM} = \mathrm{QR} \\[5pt] &\mathrm{NM} /\!/ \mathrm{QR} \end{align} \)これで,四角形\(\mathrm{NMRQ}\)について,\(1\)組の対辺が平行であり,長さが等しいことが分かったので,これは平行四辺形です。
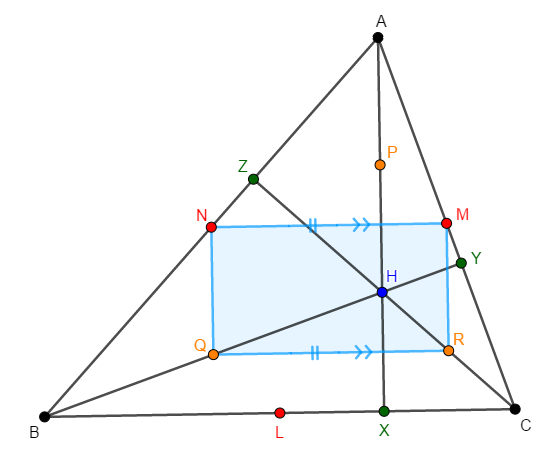
-
長方形とは,内角がすべて等しい,つまり内角がすべて直角である四角形です。 \(\angle\mathrm{QNM}\)が直角であることを証明しましょう。
先ほど確認した通り,\(\mathrm{BC} /\!/ \mathrm{NM}\)ですから,\(\mathrm{NQ} /\!/ \mathrm{AX}\)を示せば,\(\angle\mathrm{QNM}\)が\(\angle\mathrm{AXB}\)と同じく直角であることが分かります。 そのためにも,やはり中点連結定理が役立ちます。
\(\triangle\mathrm{ABH}\)に注目しましょう。 中点連結定理より,\(\mathrm{NQ} /\!/ \mathrm{AH}\)が成り立ちます。
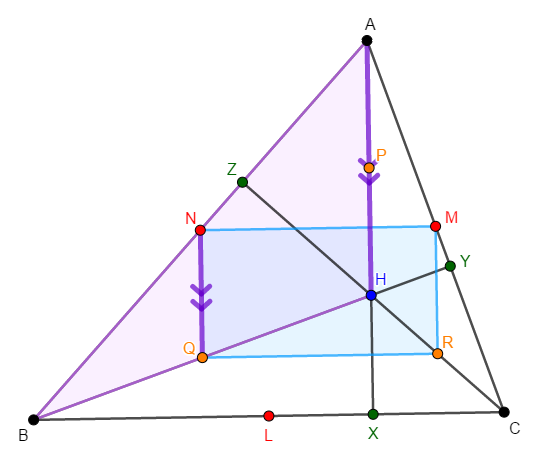
したがって,\(\mathrm{NQ} /\!/ \mathrm{AX}\)であり,\(\angle\mathrm{QNM}\)が直角であることも分かりました。
一応確認しておくと,直線\(\mathrm{NM}\),\(\mathrm{BC}\),\(\mathrm{NQ}\),\(\mathrm{AX}\)で囲まれる四角形が平行四辺形になるので,その対角が等しいことから分かります。
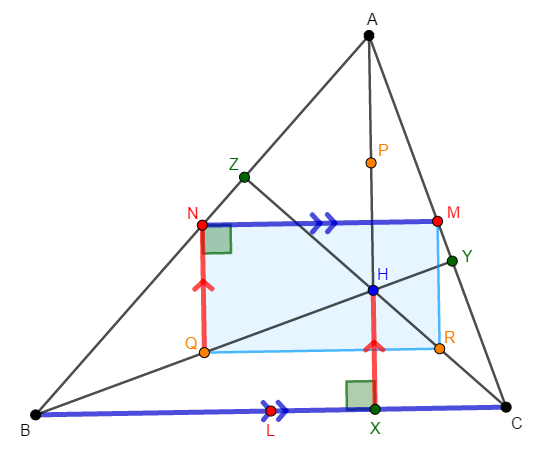
四角形\(\mathrm{NMRQ}\)は平行四辺形でしたから,同位角・錯角・対頂角による角の移動より,そのすべての内角が直角であることが分かります。 したがって,四角形\(\mathrm{NMRQ}\)は長方形です。
-
四角形\(\mathrm{NMRQ}\)は長方形ですから,対角の和が\(180^{\circ}\)になるので,これは円に内接します。 これを円\(\mathrm{O}\)とします。
さらに\(\angle\mathrm{QNM} = 90^{\circ}\)であることから,タレスの定理の逆より,弦\(\mathrm{QM}\)が円\(\mathrm{O}\)の直径であることが分かります。
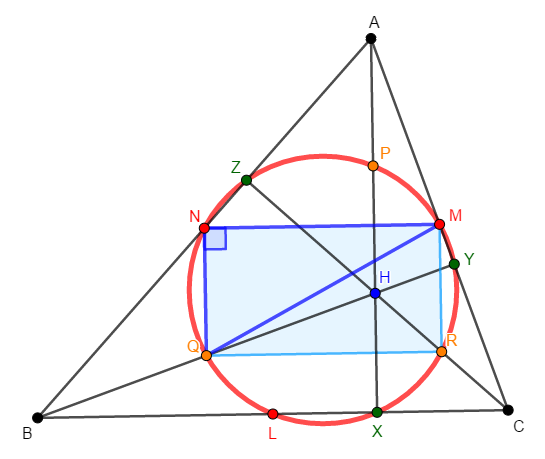
タレスの定理より,弦\(\mathrm{QM}\)に対する円周角はすべて直角です。 ここで,弦\(\mathrm{QM}\)に対する円周角に相当する角である\(\angle\mathrm{QYM}\)も直角ですから,円周角の定理の逆より,\(\mathrm{Y}\)もこの円周上の点であることが分かります。
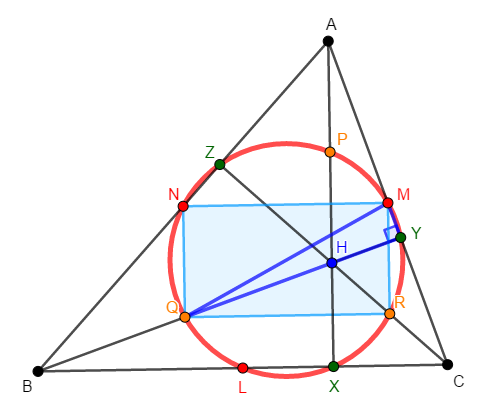
全く同様の議論で,\(\mathrm{NR}\)も直径であり,\(\angle\mathrm{NZR}\)が直角であることから,\(\mathrm{Z}\)も円\(\mathrm{O}\)の周上の点であることが分かります。 以上から,題意が示されました。
上記の議論での円周角の定理の逆について,補足しておきます。 円\(\mathrm{O}\)の周上の,弦\(\mathrm{QM}\)に関して点\(\mathrm{Y}\)と同じ側に任意の点\(\mathrm{Y}'\)をとりましょう。
点\(\mathrm{Y}\),\(\mathrm{Y}'\)が線分\(\mathrm{QM}\)に関して同じ側にあり,\(\angle\mathrm{QYM}\)と\(\angle\mathrm{QY}'\mathrm{M}\)がともに直角であり等しいので,円周角の定理の逆により,\(4\)点\(\mathrm{Q}\),\(\mathrm{M}\),\(\mathrm{Y}\),\(\mathrm{Y}'\)が共円であることが分かります。
このような議論により,円の直径\(\mathrm{AB}\)に対し,\(\angle\mathrm{A}\Box\mathrm{B}\)が直角ならば,点\(\Box\)が円周上の点であるといえるのです。
-
一度どこまで共円を示せたか,整理します。 長方形\(\mathrm{NMRQ}\)に注目することで,次図の赤い点が共円であることを示せました。 これらの点を通る円を円\(\mathrm{O}\)としました。
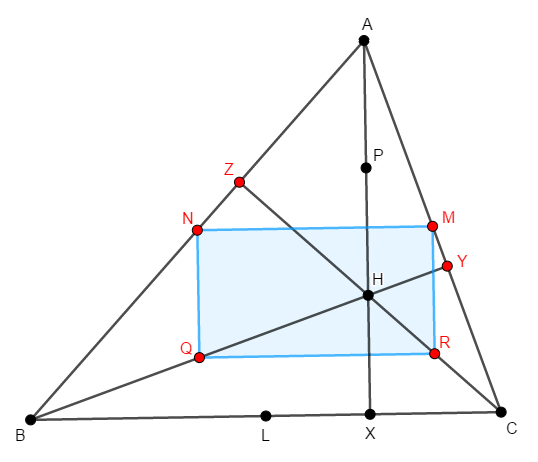
同様に四角形\(\mathrm{NLRP}\)も長方形であり,全く同様の議論により,次図の青い点が共円であることも分かります。 これらの点を通る円を円\(\mathrm{O}'\)としましょう。
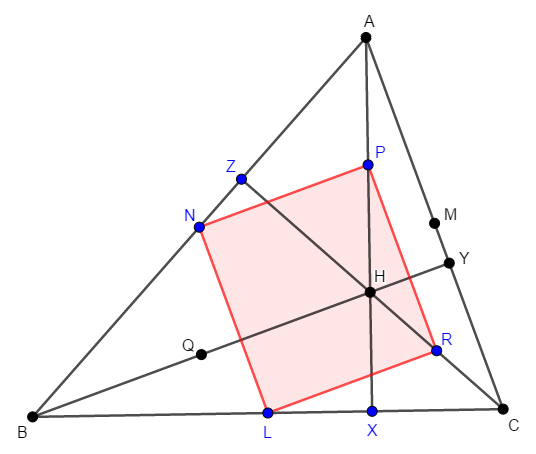
円\(\mathrm{O}\)と円\(\mathrm{O}'\)が一致することを示したいですね。 そのために,これらの情報を合わせると,次図のようになります。 どちらの円周上にもある点を緑の大きな点で表しています。
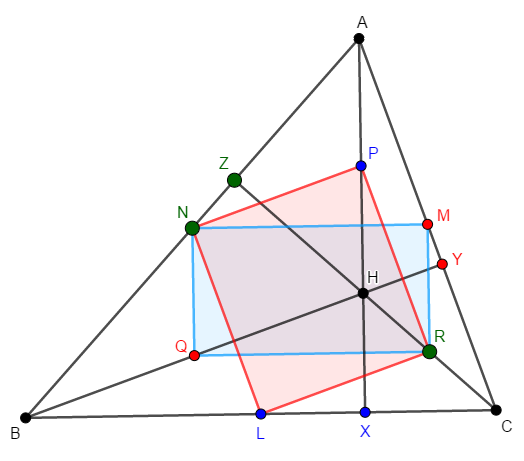
つまり,円\(\mathrm{O}\),円\(\mathrm{O}'\)はどちらも\(\triangle\mathrm{NZR}\)の外接円であり,同一の円であることが分かりました。 したがって,これら\(9\)点はすべて共円です。
もうひとつ別の見方からも証明してみましょう。 長方形\(\mathrm{NMRQ}\)の対角線である\(\mathrm{NR}\)は,円\(\mathrm{O}\)の直径でした。 また,\(\mathrm{NR}\)は長方形\(\mathrm{NLRP}\)の対角線でもあるので,円\(\mathrm{O}'\)の直径でもあります。
両者の直径が一致するということは,円の中心も弦\(\mathrm{NR}\)の中点であり一致します。 もちろん半径もともに\(\displaystyle\frac{1}{2}\mathrm{NR}\)であり一致しますから,円\(\mathrm{O}\)と円\(\mathrm{O}'\)は一致します。 したがって,題意の\(9\)点は共円です。