今回からは空間図形を学びます。 平面から空間へと舞台が変わることで,直線と直線の関係も考え直す必要があります。
目次
直線と直線の位置関係
平面図形では,直線と直線の位置関係には,大きく分けて次の\(2\)つがありました。
- \(1\)点で交わる
- 平行(交わらない)
「垂直に交わる」なども思い付くかもしれませんが,これは「\(1\)点で交わる」場合に含まれます。
さて,空間図形でも似たような位置関係が考えられそうです。 例えば,次図のような場合,直線と直線は\(1\)点で交わります。
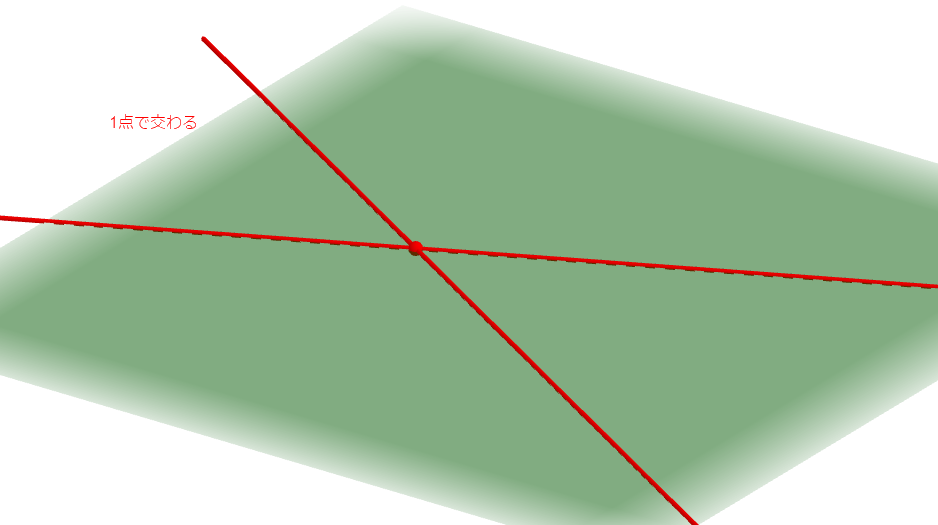
図中の緑色の四角形は,この\(2\)直線を含む平面を表しています。 今まで考えてきた平面図形の世界を,斜め上から見たものと考えてください。
上図では,緑色の平面が有限の広さに見えますが,実際は無限に広がるものだと考えてください。
平面を図に表すとき,平面を無限に広く描いてしまうと,図の背景がすべて緑色になるだけで,もはや平面の図だと認識できなくなってしまいます。 それを防ぐために,あえて有限の広さで平面を表現するのです。
このように,空間図形とはいっても,空間の中に平面を見つけることができれば,結局平面図形と同じことが考えられます。
同様に平行も考えられます。 \(2\)直線が同じ平面上にあって,交わらないとき,それらの直線は平行であるといいます。
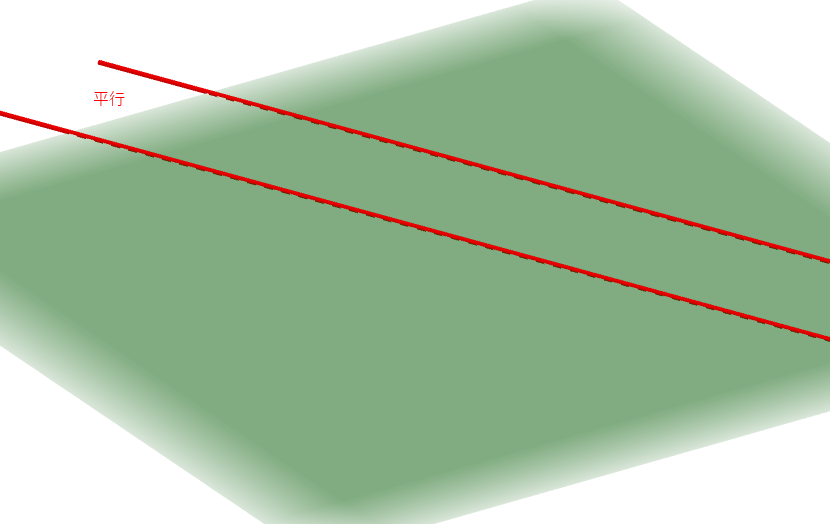
ここまでは\(2\)直線が同じ平面上にある場合を考えてきました。 その場合,平面図形と同じように考えられます。
しかし,\(2\)直線は必ずしも同じ平面にあるとは限りません。 次図のように,\(2\)直線が同じ平面上にないとき,それらはねじれの位置にあるといいます。
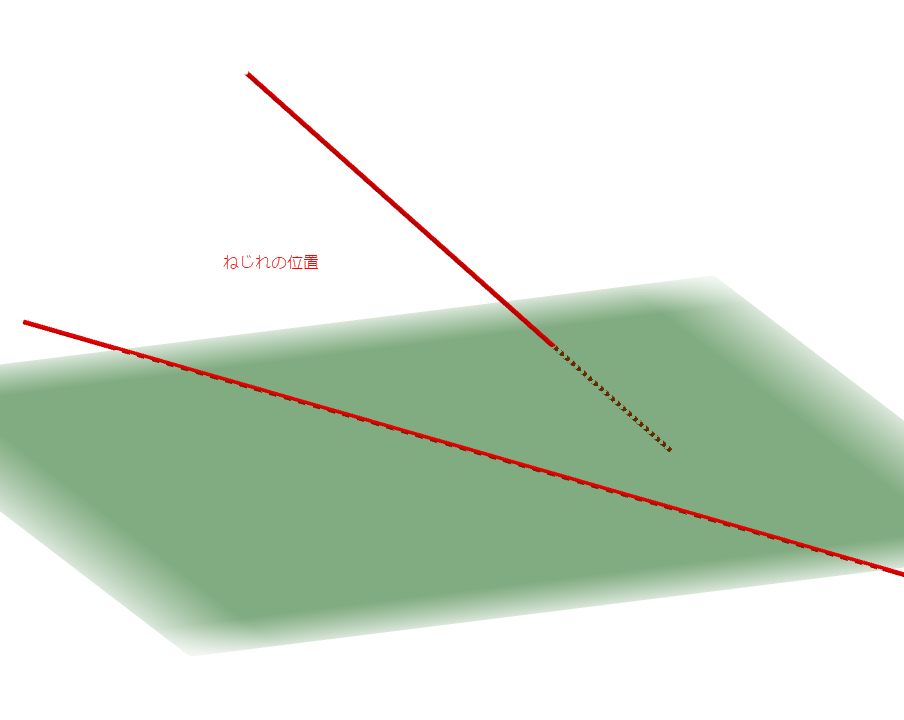
上図では,一方の直線は緑の平面上にありますが,他方はその平面上にありません。 どんな平面を考えても,これらの直線を同時に載せることはできません。
これは,もはや平面図形としては考えられません。 実際,平面図形に「ねじれの位置」なんてありませんでした。
空間図形での直線と直線の位置関係をまとめると,次のようになります。
| 位置関係 | 同一平面上 | 交点 |
|---|---|---|
| \(1\)点で交わる | ○ | ○ |
| 平行 | ○ | × |
| ねじれの位置 | × | × |
平面図形で\(2\)本の直線を考えるとき,それらのなす角が重要な情報でした。 次項ではその空間図形バージョンを考えましょう。
直線と直線のなす角
直線と直線がねじれの位置になければ,それらは同一平面上にあるのでした。 このとき,平面図形と同じように考えることができますから,それらのなす角も同一平面上で考えれば良いです。
だから空間図形でも,直線と直線が平行であるときは,それらのなす角を考えることはできません。
では,空間図形で新たに登場した「ねじれの位置」はどうでしょうか? 次図のような場合ですね。
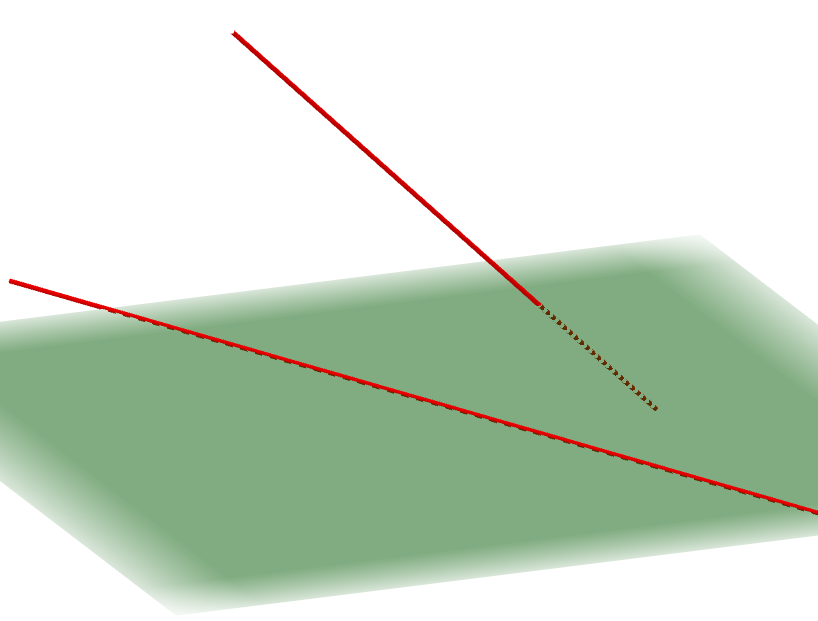
ねじれの位置も平行と同じく,直線と直線の交点がありません。 しかし,それらのなす角は考えられます。
一方の直線を平行移動して,もう一方の直線と交点を持つようにします。 次図の青い線は,緑の平面上にない方の直線を平行移動したものです。
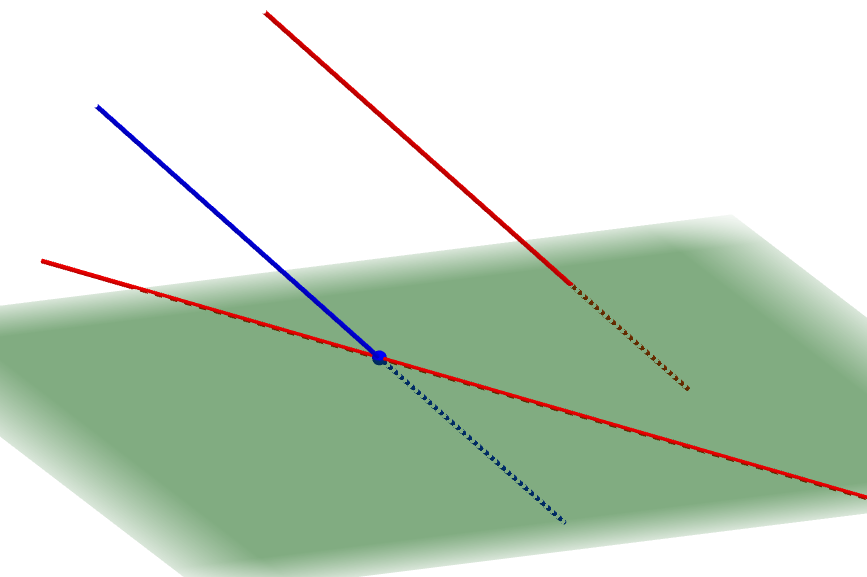
このとき,青い点で交わる\(2\)本の直線は,同一平面上にありますから,それらのなす角を考えられます。 次図は,この\(2\)直線とそれらの同一平面を図示したものです。
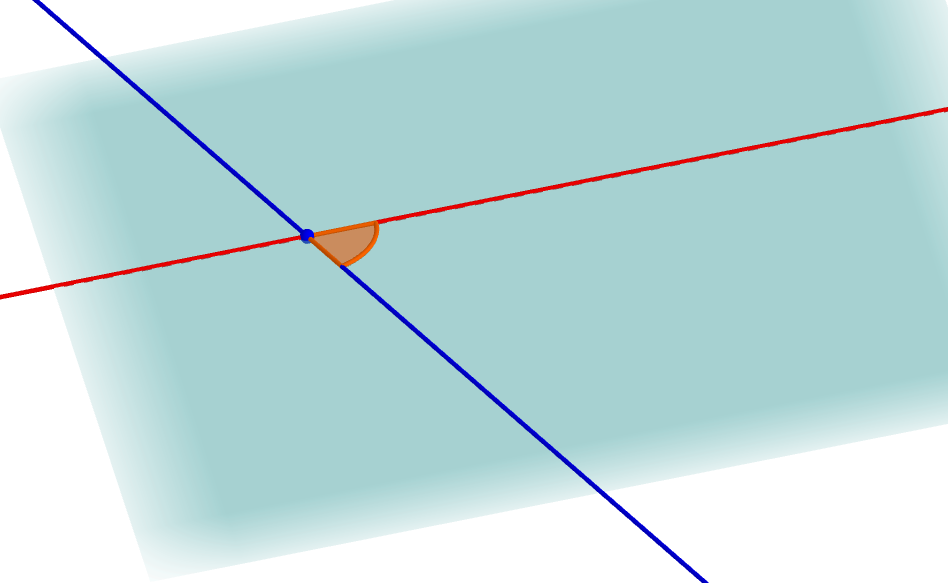
少し角度を変えて,平行移動前の直線も見えるようにすると,次図のようになります。
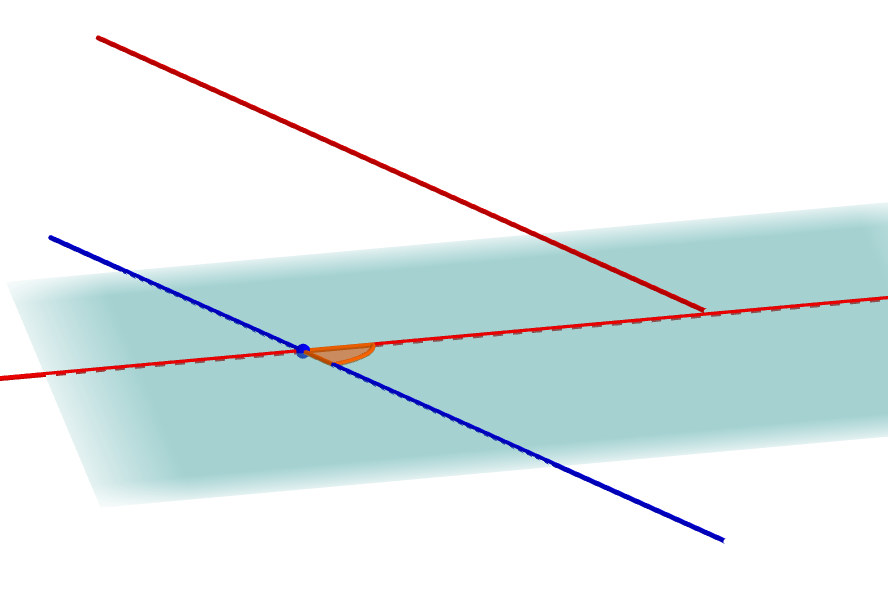
このように空間図形では,直線が直接交わっていなくても,平行移動して\(1\)点で交わるのなら,それらのなす角を考えられます。 直線と直線が平行である場合には,どんなに平行移動をしても角をなしませんから,注意しましょう。
ちなみに,垂直や直交など,平面図形で使ったなす角に関する言葉は,空間図形でも同じように使えます。
数学Aでは図形を初等幾何的に(純粋な図形問題として)扱います。 しかし,空間図形はまず描くのが大変なので,初等幾何的に扱うのが難しいこともあります。
その点,今後学ぶベクトルや座標空間は扱いやすいため,初等幾何はやりたくない!という意見も多いと思います。 ですが,ベクトルや座標空間を使うと,計算量は増える傾向にあります。
問題の状況によって,最も適切な(楽な)解き方は変わります。 様々な状況に対応できるように,初等幾何的な扱い方も学んでおくと良いと思います。
確認問題
次の\(1\)辺の長さを\(a\)とする立方体\(\mathrm{ABCD}-\mathrm{EFGH}\)について,次の(1)~(3)に答えてください。
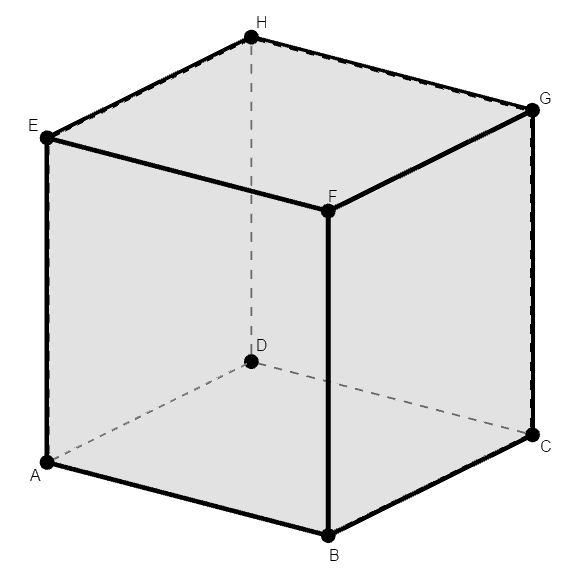
-
辺\(\mathrm{AE}\)とねじれの位置にある辺をすべて求めてください。
-
線分\(\mathrm{BG}\)と辺\(\mathrm{AB}\)のなす角を求めてください。
-
対角線\(\mathrm{AG}\)の長さを求めてください。
答え
空間が考えづらければ,平面を抜き出して考えると良いです。
-
辺\(\mathrm{AE}\)とねじれの位置にある直線は,\(\mathrm{AE}\)と同一平面上にないものです。 言い換えれば,共有点を持たず,平行でもない直線です。
まずは\(\mathrm{AE}\)と共有点を持つ辺を除外していきましょう。 除外する辺を青で表すと,次図のようになります。
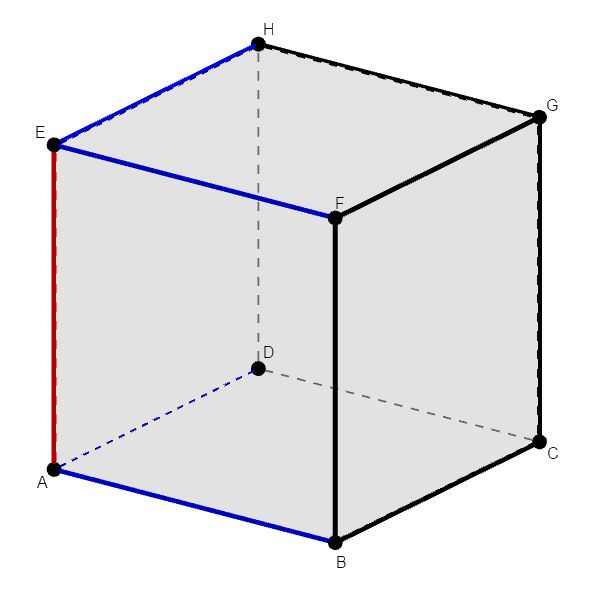
次に\(\mathrm{AE}\)と平行な辺を除外してきます。 除外する辺を緑で表すと,次図のようになります。
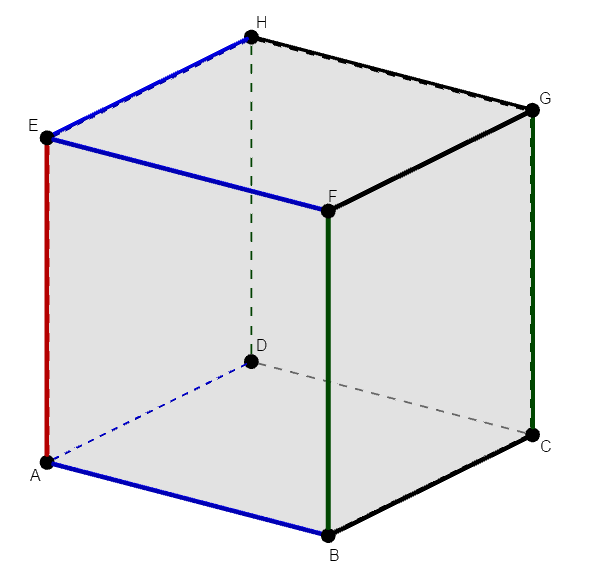
というわけで,残った辺である\(\mathrm{BC}\),\(\mathrm{CD}\),\(\mathrm{FG}\),\(\mathrm{GH}\)が辺\(\mathrm{AE}\)とねじれの位置にある辺です。
-
図を確認すると,次の通りです。
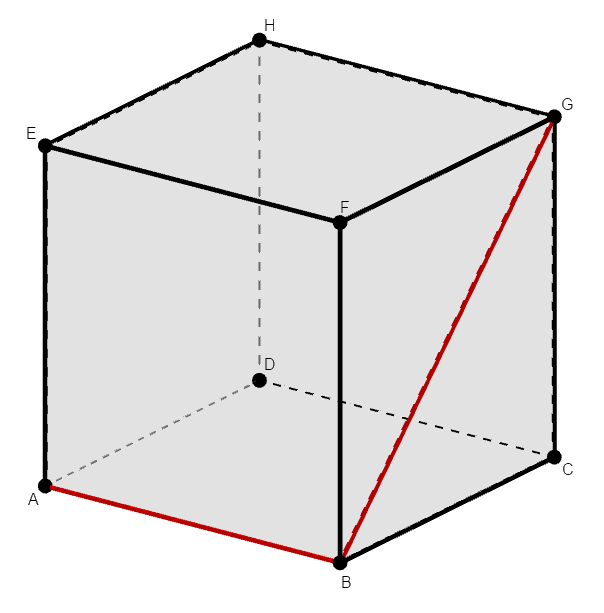
空間図形に慣れていれば,見てすぐに直角だと分かりますが,別の見方もしてみましょう。
次図のように\(\mathrm{BG}\)と平行な\(\mathrm{AH}\),\(\mathrm{AB}\)と平行な\(\mathrm{GH}\)を考えます。
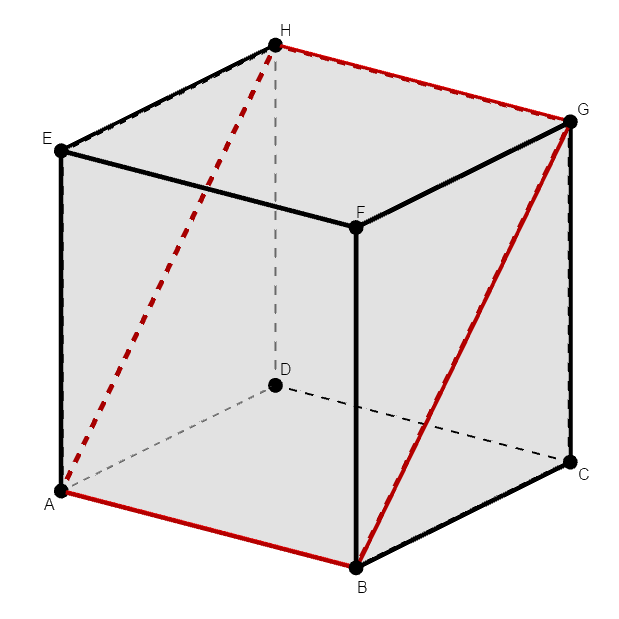
ここで,四角形\(\mathrm{ABGH}\)は平行線で囲んだ平行四辺形ですが,図形の対称性を考えれば長方形であることが分かります。 したがって,その内角は直角ですから,\(\mathrm{BG}\)と\(\mathrm{AB}\)のなす角は直角です。
-
前問で見た通り,\(\triangle\mathrm{ABG}\)は直角三角形です。 \(\mathrm{BG}\)が正方形\(\mathrm{BCGF}\)の対角線であることを考えると,\(\mathrm{BG} = \sqrt{2}a\)です。
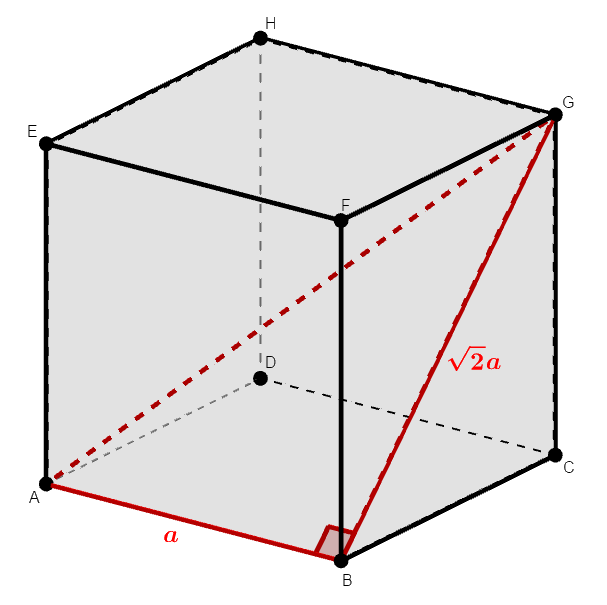
したがって,三平方の定理より,\(\mathrm{AG}\)の長さが求められます。
\( \begin{align} \mathrm{AG} &= \sqrt{\mathrm{AB}^2 + \mathrm{BG}^2} \\[5pt] &= \sqrt{a^2 + (\sqrt{2}a)^2} \\[5pt] &= \sqrt{3a^2} \\[5pt] &= \textcolor{red}{\sqrt{3}a} \end{align} \)
