引き続き空間図形を学びます。 前回は空間中の直線だけの関係を考えましたが,今回は直線と平面の関係を考えます。
目次
直線と平面の位置関係
直線と平面の位置関係を考えていきましょう。 まず当然考えられるのが,直線が平面上にある場合です。
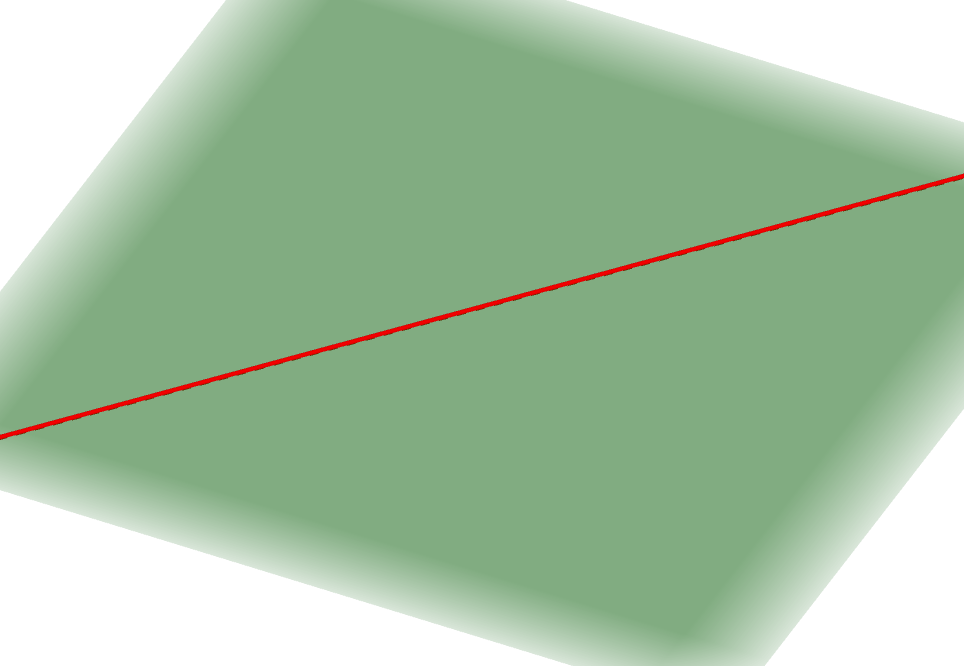
平面図形では,平面上の直線を考えてきました。 それを空間の一部として見たものが,上図です。 平面上の直線は,平面図形での直線と同じように考えられます。
次に,直線が平面上にない場合を考えましょう。 まず考えられるのが,上図で直線を平行移動し,平面の外側に出した場合です。
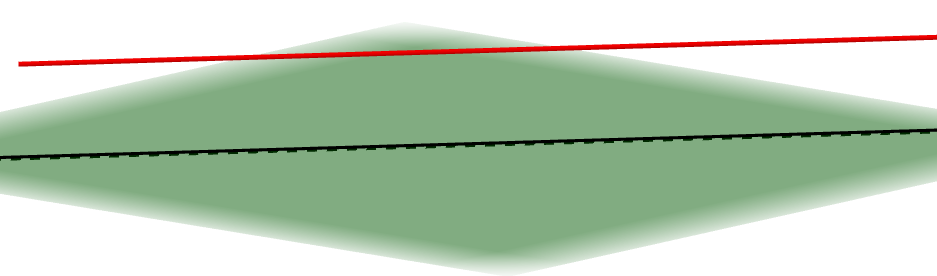
このとき,この直線と平面は平行であるといいます。 直線と直線の平行と同様に,直線と平面の平行も「直線\(/\!/\)平面」のように表します。
直線が平面上にないのは,平行である場合に限りません。 次図のように,直線と平面が\(1\)点で交わる場合も考えられます。
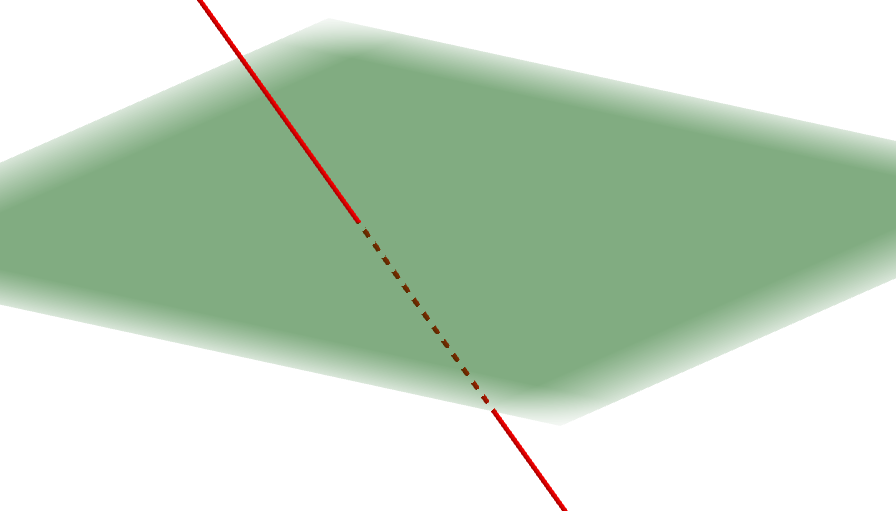
以上をまとめると,直線と平面の位置関係は,次の通りになります。
| 位置関係 | 交点数 |
|---|---|
| 直線が平面上にある | \(\infty\) |
| 平行 | \(0\) |
| \(1\)点で交わる | \(1\) |
直線と平面のなす角
平面上には色々な"向き"の直線を考えることができますから,直線と平面のなす角は考えづらそうです。 しかし,平面の"向き"をうまく考える方法があります。 平面の法線を考えるのです。
平面の法線とは,平面に垂直な直線のことです。 平面に垂直な直線とは,平面上のすべての直線に垂直な直線のことです。 図を見れば分かると思います。
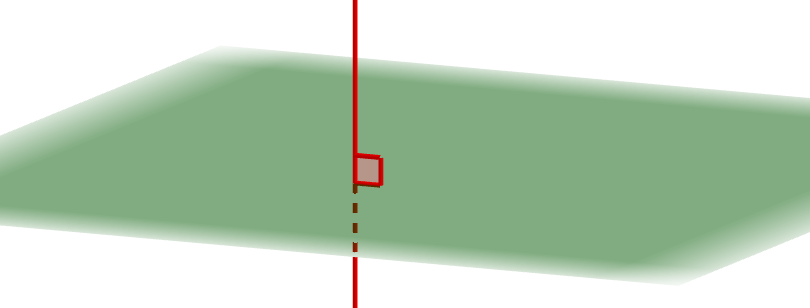
このとき,この直線はこの平面に直交するともいいます。
さて,法線を考えれば,直線と平面のなす角を考えられるといいましたが,いきなり空間で考えるのは難しいので,まずは平面図形で考えてみましょう。 次図のように\(2\)直線のなす角を考えます。
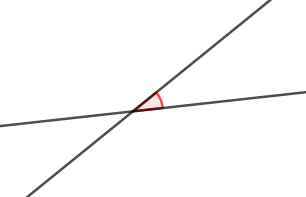
これを敢えて法線を使って考えます。 右上に走っている方の直線の代わりに,その法線(青色)を考えます。
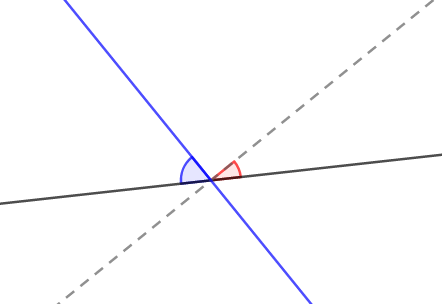
この法線と元の直線(薄い破線)のなす角は直角ですから,この法線ともう一方の直線がなす角(青色)は,もともと考えていた角(赤色)の余角です。 つまり,青と赤の角の和は直角になります。
したがって,赤い角は青い角の余角として求められます。 法線を使えば,直線と直線のなす角を間接的に求められるのです。
同様に直線と平面のなす角も,平面の代わりにその法線を考えれば,間接的に求められます。 詳しくは空間ベクトルの章で学び,数学Aでは学びませんが,その準備として「垂直」の概念は理解しておきましょう。
直線が平面に垂直であることを示すには,次の定理が使えます。 証明は確認問題とします。
直線\(\ell\)が平面\(\alpha\)上の交わる\(2\)直線に垂直であるとき,\(\ell\)は\(\alpha\)に垂直である。
確認問題
直線\(\ell\)が平面\(\alpha\)に垂直であるとは,\(\ell\)が\(\alpha\)上の任意の直線に垂直であることでした。 しかし,すべての直線を考えるのは,簡単なことではありません。
実は,「\(\ell\)が\(\alpha\)に垂直であるためには,\(\alpha\)上の交わる\(2\)直線に垂直であれば十分」です。 なんと\(2\)直線だけでOKなのです。(平行だとダメですが。)
太字部を証明してください。
答え
\(\ell\)と\(\alpha\)の交点を\(\mathrm{X}\)とします。 \(\ell\)は\(\alpha\)上の交わる\(2\)直線に垂直ですが,その\(2\)直線を\(\mathcal{m}\),\(\mathcal{n}\)とします。 直線同士のなす角は,平行移動して考えても良いのですから,\(\mathcal{m}\),\(\mathcal{n}\)は\(\mathrm{X}\)で交わるとしても良いです。
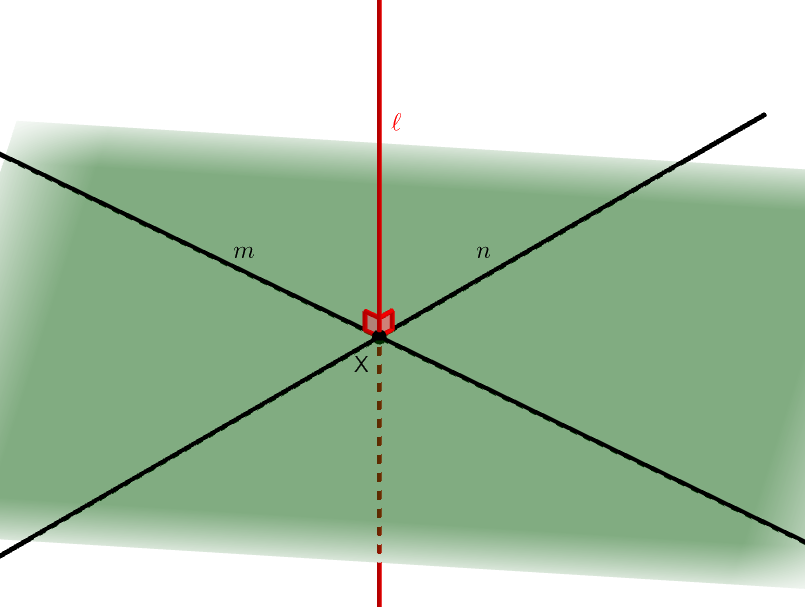
証明したいのは,\(\ell\)が\(\alpha\)上の任意の直線に垂直であることです。 直線同士のなす角は,平行移動して考えても良いのですから,任意の直線は\(\mathrm{X}\)を通るように移動して考えられます。
したがって,\(\mathrm{X}\)を通る\(\alpha\)上の任意の直線(\(\mathcal{m}\),\(\mathcal{n}\)以外)を考えて,これが\(\ell\)と直交することを示せば良いです。 そのような直線を青線で表します。
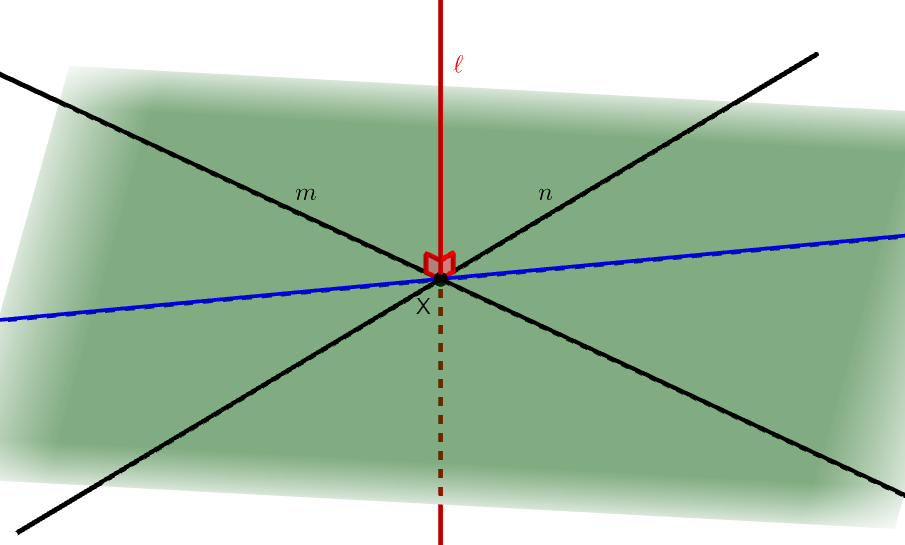
ここで,まず\(\ell\)が\(\mathcal{m}\),\(\mathcal{n}\)と直交するという情報を活用するため,\(\mathcal{m}\),\(\mathcal{n}\)上に次のように\(\mathrm{X}\)から等距離の点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\),\(\mathrm{S}\)をとります。 \(\mathrm{X}\)を中心とする適当な円との交点をとれば良いです。
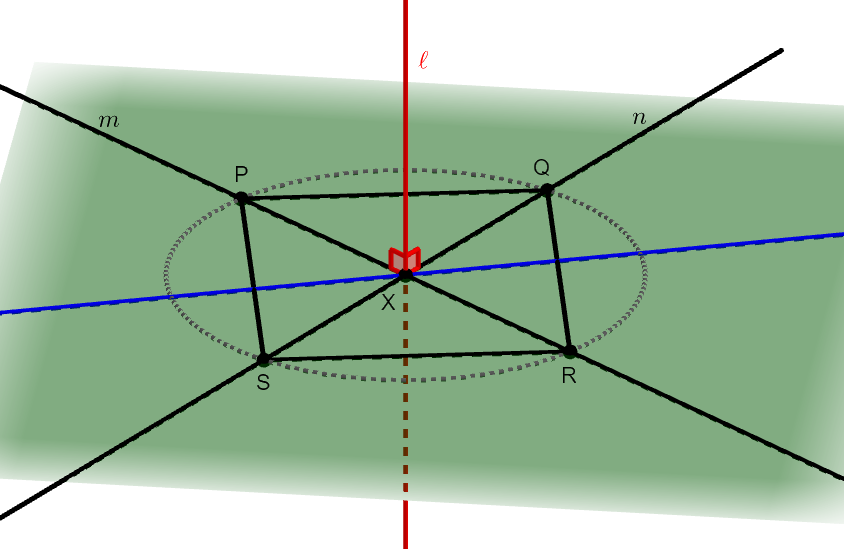
さらに,青線と\(\mathrm{PS}\),\(\mathrm{QR}\)の交点をそれぞれ\(\mathrm{Y}\),\(\mathrm{Z}\)とします。 あとは\(\ell\)上に\(\mathrm{X}\)でない点\(\mathrm{O}\)をとって,\(\angle\mathrm{OXY} = 90^{\circ}\)を示すだけです。
(青線の引き方によっては,\(\mathrm{PQ}\),\(\mathrm{SR}\)との交点を考えることになりますが,後の議論は同様です。)
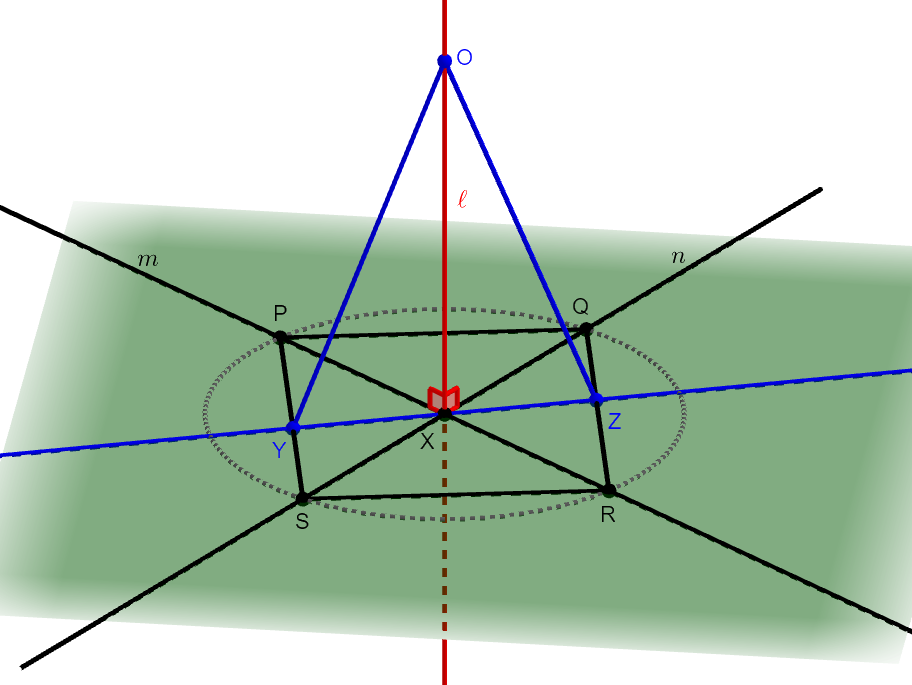
目標は,\(\angle\mathrm{OXY}\)または\(\angle\mathrm{OXZ}\)が直角であることを示すことですが,図を見た感じ\(\triangle\mathrm{OXY}\)と\(\triangle\mathrm{OXZ}\)の合同を示せそうです。 その際,\(\angle\mathrm{OXY}\)と\(\angle\mathrm{OXZ}\)は対応する角になりそうですから,その和が\(180^{\circ}\)であることを考えると,それぞれ直角であることが分かります。
まず\(\mathrm{XY} = \mathrm{XZ}\)を示します。 点\(\mathrm{X}\)の周りの対頂角,弧\(\mathrm{SR}\)に対する円周角に注目すれば,次が成り立つことが分かります。
\(\mathrm{XQ} = \mathrm{XR}\)ですから,\(\triangle\mathrm{XQR}\)は二等辺三角形です。 その底角は等しいので,上の\(2\)つめの式から\(\angle\mathrm{SPR} = \angle\mathrm{QRP}\)が成り立つことが分かります。
また,\(\mathrm{XP} = \mathrm{XR}\)ですから,\(1\)辺とその両端の角がそれぞれ等しいので,\(\triangle\mathrm{XPY}\)と\(\triangle\mathrm{XRZ}\)は合同です。 したがって,対応する辺が等しいので,\(\mathrm{XY} = \mathrm{XZ}\)が成り立ちます。
次に\(\mathrm{OY} = \mathrm{OZ}\)を示します。 そのために,まず\(\mathrm{O}\)から\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\),\(\mathrm{S}\)に線分を引きます。
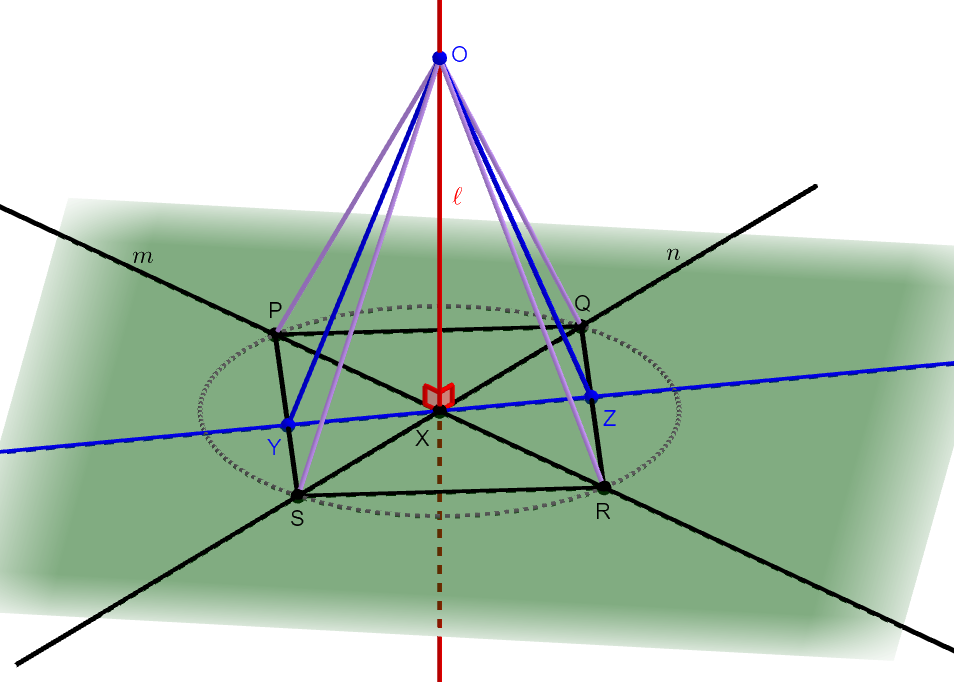
ここで遂に\(\mathcal{m}\),\(\mathcal{n}\)が\(\ell\)と直交することを利用します。 \(\mathrm{XP} = \mathrm{XR}\)であり,\(\mathrm{OX}\)が共通なのですから,直角三角形\(\triangle\mathrm{OXP}\),\(\triangle\mathrm{OXR}\)で三平方の定理を適用することにより,\(\mathrm{OP} = \mathrm{OR}\)が分かります。 同様に\(\mathrm{OS} = \mathrm{OQ}\)も分かります。
また,先ほど確認した\(\triangle\mathrm{XPY}\)と\(\triangle\mathrm{XRZ}\)の合同により,\(\mathrm{PY} = \mathrm{RZ}\)が成り立ちます。 あとは\(\angle\mathrm{OPY} = \angle\mathrm{ORZ}\)を示せば,\(\triangle\mathrm{OPY}\)と\(\triangle\mathrm{ORZ}\)の合同から\(\mathrm{OY} = \mathrm{OZ}\)が示せます。
ここから少し寄り道が必要です。 \(\angle\mathrm{OPY} = \angle\mathrm{ORZ}\)を示すには,\(\triangle\mathrm{OPS}\)と\(\triangle\mathrm{ORQ}\)が合同であることがいえれば良いです。 \(\mathrm{OP} = \mathrm{OR}\),\(\mathrm{OS} = \mathrm{OQ}\)は分かっていますから,あとは\(\mathrm{PS} = \mathrm{RQ}\)を示せば良いですね。 そしてそのためには,\(\triangle\mathrm{XPS}\)と\(\triangle\mathrm{XRQ}\)の合同を示せば良いです。
その証明は簡単です。 \(\mathrm{XP} = \mathrm{XR}\),\(\mathrm{XS} = \mathrm{XQ}\)であり,対頂角より\(\angle\mathrm{PXS} = \angle\mathrm{RXQ}\)ですから,\(2\)辺とその間の角がそれぞれ等しいので,\(\triangle\mathrm{XPS}\)と\(\triangle\mathrm{XRQ}\)は合同です。 したがって,対応する辺が等しいので,\(\mathrm{PS} = \mathrm{RQ}\)です。
あとは先に確認した論理の流れによって,\(\triangle\mathrm{OPS}\)と\(\triangle\mathrm{ORQ}\)の合同が分かり,\(\angle\mathrm{OPY} = \angle\mathrm{ORZ}\)が分かり,\(\triangle\mathrm{OPY}\)と\(\triangle\mathrm{ORZ}\)の合同が分かるため,\(\mathrm{OY} = \mathrm{OZ}\)であることが分かります。
したがって,\(\mathrm{XY} = \mathrm{XZ}\),\(\mathrm{OY} = \mathrm{OZ}\)が成り立ち,\(\mathrm{OX}\)が共通ですから,\(3\)辺がそれぞれ等しいので,\(\triangle\mathrm{OXY}\)と\(\triangle\mathrm{OXZ}\)は合同です。 よって,対応する角である\(\angle\mathrm{OXY}\),\(\angle\mathrm{OXZ}\)が等しく,その和は\(180^{\circ}\)なので,それぞれの角は直角です。
以上から,\(\ell\)は\(\alpha\)上の任意の直線に垂直なので,\(\ell\)は\(\alpha\)に垂直です。
