平面と平面の位置関係

はじめに

直線と直線，直線と平面の位置関係について考えた後は，もちろん平面と平面の位置関係について考えます。

平面と平面の位置関係

▼

空間内での平面同士の位置関係は，平面内での直線の位置関係と同じように，\(2\)通りだけです。

平面内では，直線同士は交わるか，平行で交わらないかです。空間内での平面同士も交わるか，平行で交わらないかです。図をイメージできれば分かるでしょう。

まずは平面同士が交わる場合を考えます。このときの図を見てください。

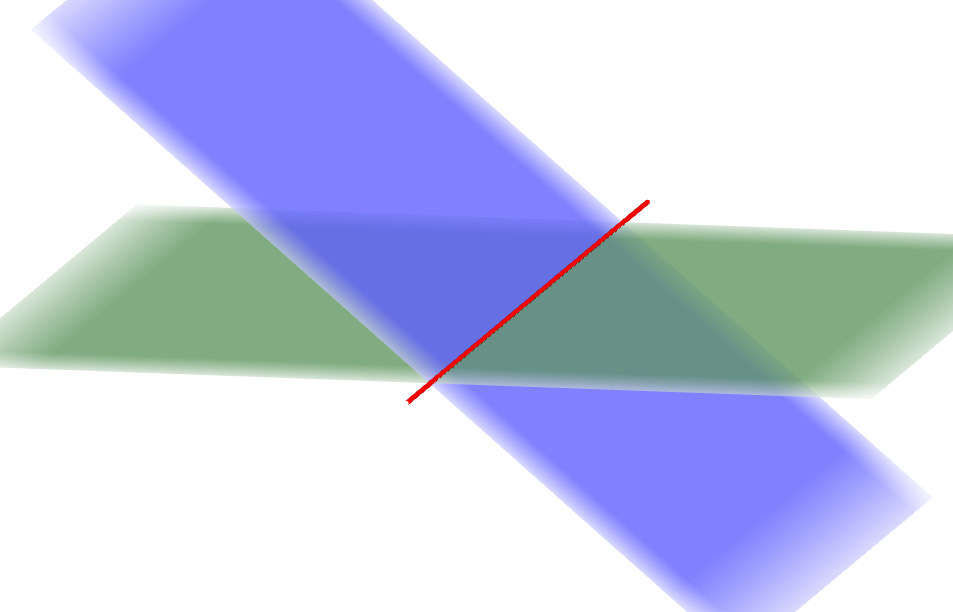
直線と直線が交わるとき，\(1\)つの交点ができます。平面と平面が交わるときは，上図のように\(1\)本の交線ができます。

直線同士のなす角を考えたときのように，平面同士のなす角も考えられますが，それは次項で学ぶことにしましょう。

続いて，平面の平行を考えます。このときの図を見てください。

直線同士や直線と平面の平行と同様に，平面同士の平行も「平面\(/\!/\)平面」のように表します。平行な平面同士には共有点がありませんね。

平面同士の位置関係には，以上の\(2\)種類しかありません。まとめておきましょう。

位置関係	共有点
交わる	共線ができる
平行	なし

平面と平面のなす角

▲

▼

平面と平面のなす角をどう考えるか，何となく想像はつくと思います。次図のオレンジの角の感じでしょう。

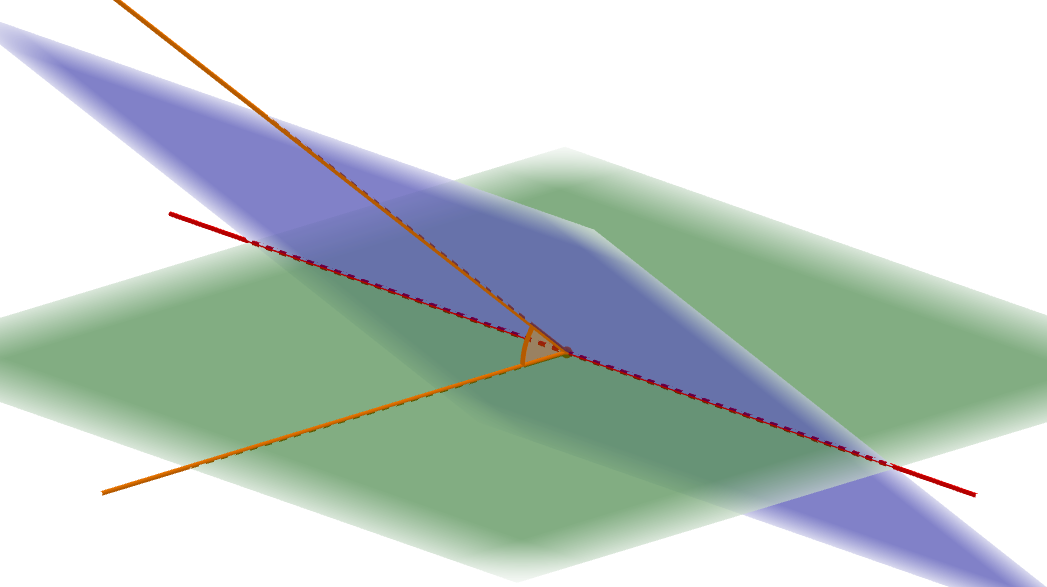
各平面から引いた直線（オレンジ）を合流させ，その間の角を見ていますね。ですが，当然どんな直線でも良いわけではありません。

平面間の角を考えるには，平面の向きを代表するようなオレンジ線を引く必要があります。そのためには，交線に向かって垂直に直線を引くべきです。

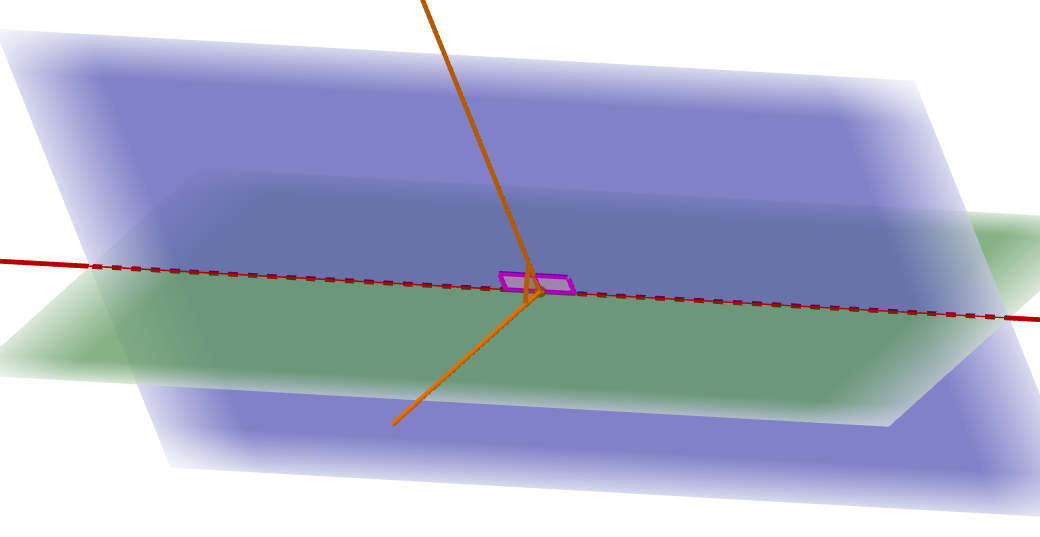
オレンジ線が交線に垂直であれば，それは平面に「沿う」形になります。したがって，オレンジ線のなす角が，平面同士のなす角だといえるのです。

平面同士のなす角が直角であるとき，それらは垂直であるとか，直交するなどいうことは，直線同士や直線と平面のなす角を考えたときと同様です。

確認問題

▲

三角比を学んだ人向けの問題です。正四面体の\(2\)つの面がなす角を\(\theta\)とするとき，\(\cos\theta\)の値を求めてください。

まだ三角比を学んでいない人は，適当な正四面体を描いて，角\(\theta\)を図示してください。

答え

まずは図をかいて状況把握です。

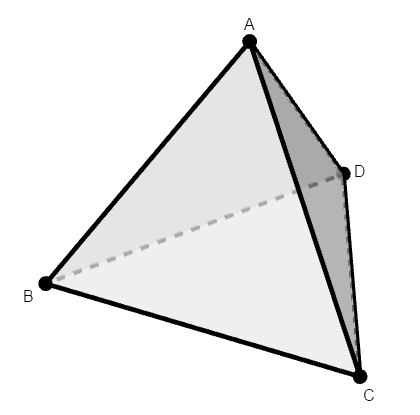
正四面体の対称的な形から，\(2\)つの面のなす角は，どの面について考えても構いません。面\(\mathrm{ABC}\)と面\(\mathrm{DBC}\)のなす角を考えることにしましょう。

交線は辺\(\mathrm{BC}\)ですから，各面上で\(\mathrm{BC}\)に垂直な直線を引きましょう。

各面が正三角形であることに注意すると，\(\mathrm{BC}\)の垂直二等分線はその対角を通りますから，考えやすいですね。 \(\mathrm{BC}\)の中点を\(\mathrm{M}\)として，面\(\mathrm{ABC}\)で垂線\(\mathrm{AM}\)と面\(\mathrm{DBC}\)での垂線\(\mathrm{DM}\)を引きます。

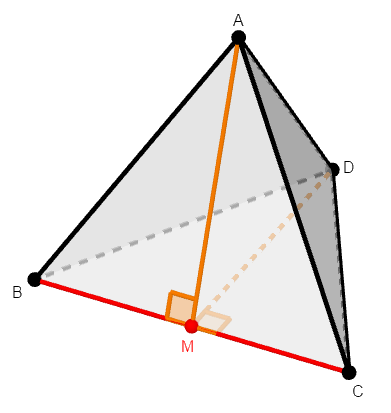
\(\mathrm{AM}\)と\(\mathrm{DM}\)のなす角が\(\theta\)ですね。それを求めるために，\(\triangle\mathrm{MAD}\)を抜き出してかきます。

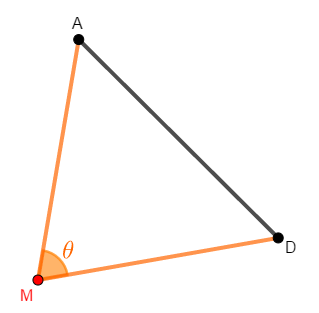
ここからは三角比の知識が必要です。余弦定理で\(\cos\theta\)の値を求めるため，各辺の長さを求めましょう。正四面体の\(1\)辺の長さを\(a\)とします。（単純に\(1\)として進めても良いです。）

\(\triangle\mathrm{ABM}\)に注目すると，\(60^{\circ}\)の角を持つ直角三角形の三角比から，\(\mathrm{AM} = \displaystyle\frac{\sqrt{3}}{2}a\)です。 \(\mathrm{DM}\)も同じ長さですね。 \(\mathrm{AD}\)は正四面体の辺ですから，その長さは\(a\)です。

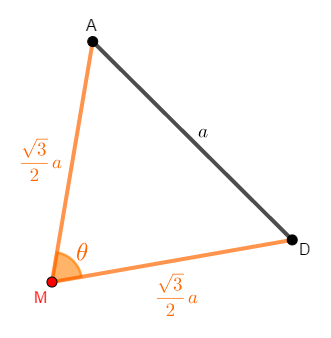
あとは余弦定理により，\(\cos\theta\)を求めるだけです。

\( \begin{align} \cos\theta &= \displaystyle\frac{\mathrm{AM}^2 + \mathrm{DM}^2 - \mathrm{AD}^2}{2 \cdot \mathrm{AM} \cdot \mathrm{DM}} \\[5pt] &= \displaystyle\frac{\left(\displaystyle\frac{\sqrt{3}}{2}a\right)^2 + \left(\displaystyle\frac{\sqrt{3}}{2}a\right)^2 - a^2}{2 \cdot \displaystyle\frac{\sqrt{3}}{2}a \cdot \displaystyle\frac{\sqrt{3}}{2}a} \\[5pt] &= \displaystyle\frac{\displaystyle\frac{3}{4} + \displaystyle\frac{3}{4} - 1}{\displaystyle\frac{3}{2}} \\[5pt] &= \displaystyle\frac{\displaystyle\frac{1}{2}}{\displaystyle\frac{3}{2}} \\[5pt] &= \textcolor{red}{\displaystyle\frac{1}{3}} \end{align} \)

この\(\theta\)は\(70.5^{\circ}\)くらいです。 \(60^{\circ}\)ではないので注意です。