空間図形の最後に,多面体について学びます。 正多面体やオイラーの多面体定理について理解しましょう。
目次
多面体
多面体とは,いくつかの平面で囲まれた立体のことです。 直方体や四面体など,小学生の頃から色んな多面体を学習してきました。
一方,円錐や球は多面体ではありません。 平面のみならず,曲面を含む立体だからですね。
次のような立体も多面体です。 平面に囲まれてできていますね。
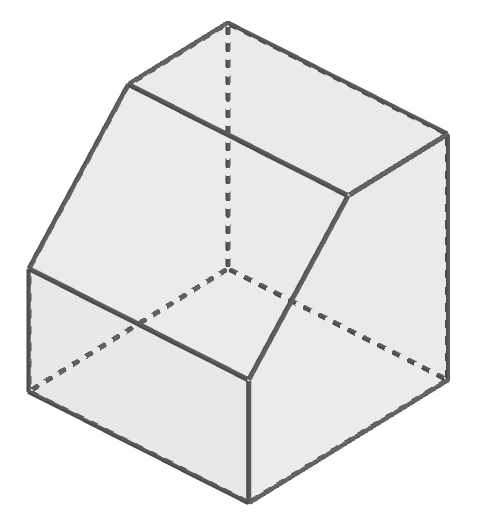
このように凹みのない立体を凸多面体といいます。 次のように凹みがある立体は凹多面体といいますが,学校ではあまり扱いません。
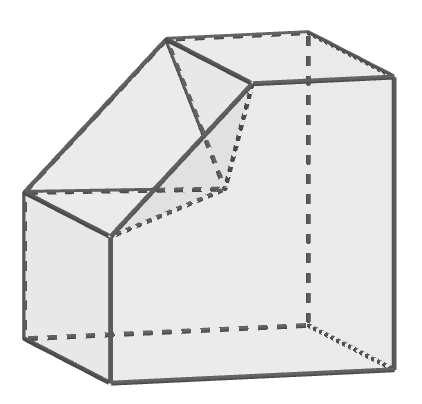
ここでも主に凸多面体について考えることにします。
オイラーの多面体定理
凸多面体の頂点(vertex),辺(edge),面(face)の数について,次の定理が成り立ちます。
凸多面体の頂点の数を\(v\),辺の数を\(e\),面の数を\(f\)とすると,次の等式が成り立つ。
オイラーの多面体定理は,凹多面体でも穴さえ開いていなければ成り立ちます。 しかし,凹多面体はあまり扱われないので,気にしなくても良いかと思います。
定理の内容が,高校では習わないグラフ理論から来ているので,証明は省略されることが多いです。
グラフ理論は,複雑な数式でゴリゴリ進めるものではないので,中学生でも学べば理解できる部分も多いです。 しかし,いろいろ予備知識の導入が必要なのも事実なので,ここではざっくりした証明だけ見てみましょう。
例として次のような多面体を考えます。
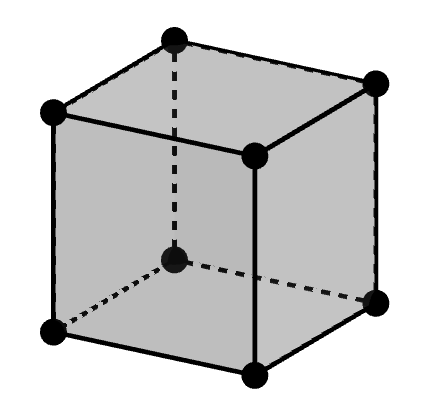
この多面体では,\(v = 8\),\(e = 12\),\(f = 6\)ですから,確かに\(v - e + f = 2\)が成り立ちます。
しかし,もちろん\(1\)つの多面体に対して確認しただけでは,定理を証明したことにはなりません。 この例を手掛かりに,もっと一般化して考えましょう。
まず,立体のまま考えるのは大変なので,情報を平面の世界に落とし込みます。 そのために,次のように面を\(1\)つ取り除いてみます。
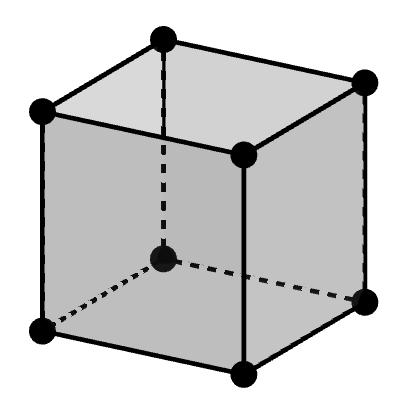
分かりづらいかもしれませんが,上の面を取り除きました。 面を\(1\)つ除いたのですから,\(v - e + f = 1\)を示すのが今後の目標です。
ここで考えたいのは,頂点,辺,面の数だけですから,その数さえ変わらなければ,辺や面を伸び縮みさせても構いません。 そこで上の図を「開いてぺたんと広げる」ことで,次図のように平面に落とし込めます。
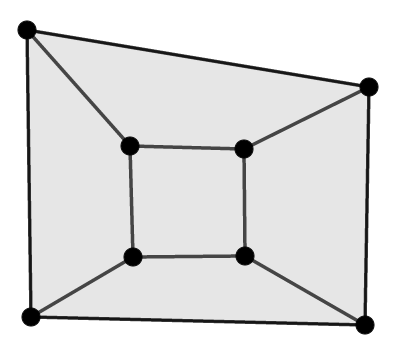
この図は,先ほどの図と頂点,辺,面の数が変わりません。 つまり立体のときの情報を残したまま,平面の問題に置き換えたのです。 この図で\(v - e + f = 1\)を証明すれば良いですね。
先ほど多面体の面を\(1\)つ取り除いたのは,このように多面体を開くためだったのでした。
さて,確認したいのは\(v - e + f\)の値が\(1\)になることなのですが,少し工夫が必要です。 まず,面を取り囲む辺を\(1\)つずつ除いていきます。
なぜそんなことをするのか? それは,この操作によって,辺と面がちょうど\(1\)つずつ減るからです。 まず次図を見てください。
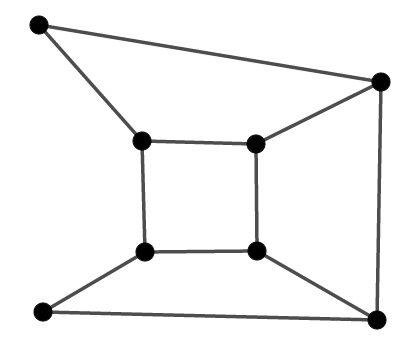
この図は左端の辺を除いたものですが,確かに左側の面も\(1\)つ無くなっています。 次のような場合も見てみましょう。
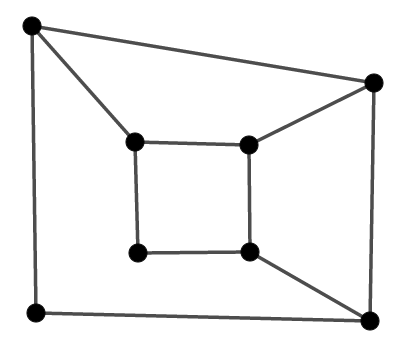
この図はある面と面の間の辺を除いたものですが,\(2\)つの面が合体して\(1\)つになっています。 つまり,この場合でも面が\(1\)つ減っているのです。
さて,この操作で大事なのは,\(e\)と\(f\)が\(1\)ずつ,つまり同数減ることです。 このとき,\(v - e + f\)の値は変わりませんね。 この操作によって,辺,面を減らし,よりシンプルな形にできるのです。
この操作を面の数だけ繰り返せば,ついに面はなくなります。 そして\(v - e + f\)の値は変わらず維持されています。
当然ですが,面は辺に囲まれてできているので,\(e > f\)です。 したがって,面がなくなるまで,辺を除く操作を繰り返すことが確実にできます。
面がすべてなくなれば,\(f = 0\)になるので,後は\(v - e = 1\)を確認すれば良いことになります。 先ほどの図で最後まで操作を行ったのが,次図です。 (どの辺を除いたかで形は変わります。)
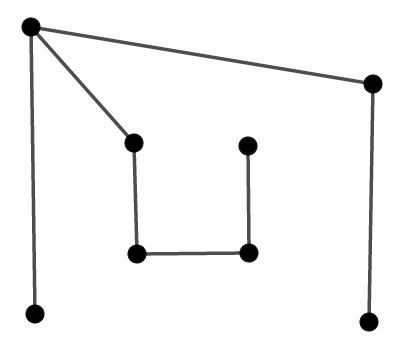
面がないということは,辺で囲まれた領域が存在しないということです。 つまりこの段階で,この図はいくつかの枝で出来た「枝分かれ」になります。
次は枝の末端から「頂点と辺のペア」を除いていきます。 当然\(v - e\)の値は維持され,変わりません。
試しに先ほどの図からペアを\(1\)つ除くと,次図のようになります。
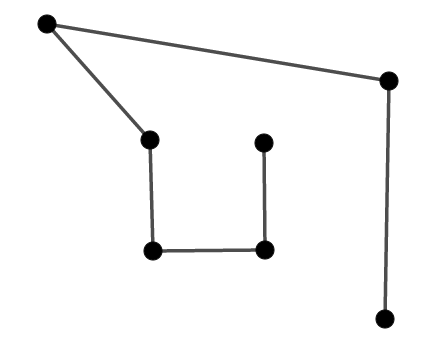
辺の両端には頂点がありますから,当然\(v > e\)です。 したがって,辺がなくなるまでこの操作を繰り返すことができます。 もちろん,\(v - e\)の値は維持されたままです。
先ほどの図が「枝分かれ」であったことを思い出すと,枝を末端からカットしていくことで,最終的には根元の\(1\)点だけが残ることが分かります。 つまり\(v = 1\)です。
以上の議論から,元の多面体から面を\(1\)つ除いた図形において,\(v - e + f = 1\)が成り立つことが分かり,オイラーの多面体定理の成立が確認できました。
ざっくりした箇所については,グラフ理論の本などで「オイラーの定理」の証明を確かめてみてください。
上の議論は,「穴の開いていない」凹多面体についても成り立つことが分かります。 穴が開いていなければ,同じように面を\(1\)つ除いて,平面化できるからです。
正多面体
正多面体とは,次の条件を満たす凸多面体のことです。
- すべての面が合同の正多角形である。
- 各頂点に集まる面の数が等しい。
つまり,かなり対称的な形の多面体ですね。 次の正四面体(正三角錐),正六面体(立方体)はよく知っていますね。
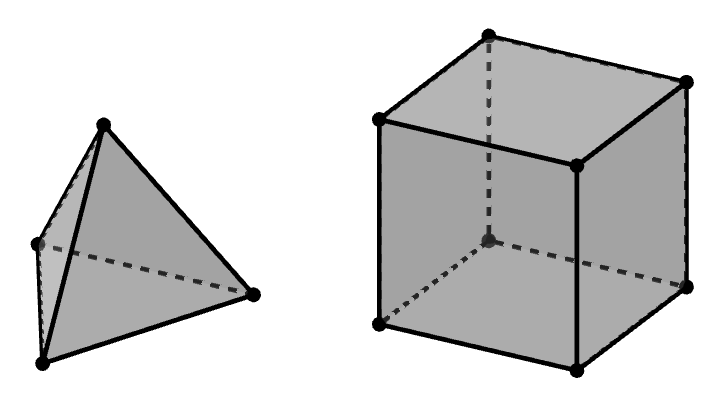
正多面体にどんなものがあるのかを考えるには,まず次の多面体の性質を知っておくと良いです。
多面体の\(1\)つの頂点に集まる面・角について,次が成り立つ。
- \(3\)つ以上の面が集まる。
- 凸多面体の場合,集まる角の大きさは合計\(360^{\circ}\)未満である。
\(1\)つめの性質は良いですね。 もし頂点に集まる面が\(2\)つだけなら,面で囲まれた空間を作ることはできません。 面を曲げてしまえば出来そうですが,曲面を使ったものを多面体とは言いません。
\(2\)つめの性質については,その頂点に掌を当てて,多面体を潰すのをイメージしてください。 多面体は潰れ,頂点の周りの面が平面状に広がります。
このとき,必ず頂点の周りの平面には「隙間」が出来るはずです。 隙間がなければ,改めて面を立体状に折ったとき,面同士が重なってしまい,多面体に戻せないのでおかしいです。 隙間があるということは,角度の合計が\(360^{\circ}\)未満なのです。
正\(N\)角形の\(1\)つの内角の大きさは\(180^{\circ} \times \displaystyle\frac{N - 2}{N}\)です。 表にすれば次の通りですね。 角が増えれば,内角も大きくなるのです。
| 正多角形 | \(1\)つの内角 |
|---|---|
| 正三角形 | \(60^{\circ}\) |
| 正四角形 | \(90^{\circ}\) |
| 正五角形 | \(108^{\circ}\) |
| 正六角形 | \(120^{\circ}\) |
正多面体の性質より,\(1\)つの頂点には最低\(3\)つの面が集まります。 さらにそれらの内角を\(1\)回ずつ足すと,\(360^{\circ}\)未満になるはずです。
したがって,正多面体の面として相応しいのは,正三角形,正四角形,正五角形だけです。 正六角形以上だと,内角\(3\)つで\(360^{\circ}\)以上になってしまうからです。
面が正三角形である多面体は,頂点に集まる正三角形が\(3\)つ,\(4\)つ,\(5\)つの場合の\(3\)パターンです。 それぞれ頂点に集まる角度の合計が\(180^{\circ}\),\(240^{\circ}\),\(300^{\circ}\)であり,凸多面体の性質を満たしますね。
同様に考えると,面が正四角形,正五角形である多面体は,頂点に集まることの出来る面の数が\(3\)しかありえません。 以上から,正多面体は\(5\)種類しか存在しないのです。
| 面 | 頂点に集まる面数 |
|---|---|
| 正三角形 | \(3\) |
| 正三角形 | \(4\) |
| 正三角形 | \(5\) |
| 正四角形 | \(3\) |
| 正五角形 | \(3\) |
それぞれの場合で,どんな多面体ができるのでしょうか? 例えば,正三角形が\(1\)つの頂点に\(5\)つ集まる場合を考えます。 このとき,\(1\)つの頂点に集まる辺の数も\(5\)です。
頂点を真上から見た図をイメージしてください。 頂点の周りに\(5\)つの面があるのなら,辺の数も\(5\)つであることが分かります。
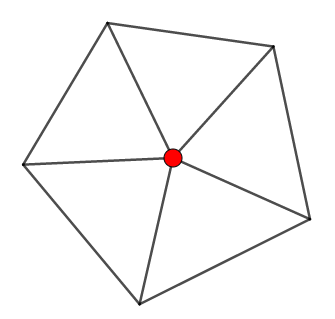
したがって,頂点の周りに集まる辺を合計すると,\(5v\)本になります。 もちろんこれは,同じ辺を何回か重複して数えたものです。
どれくらい重複して数えたかというと,辺の両端に頂点があることを考えると,\(2\)回ずつカウントしてしまっていることが分かります。 したがって,次が成り立ちます。
また,重複して数えた辺の数\(5v\)は,面を囲む辺として活用されます。 面は三角形ですから,\(3\)本で\(1\)つの面になるので,次が成り立ちます。
これらをオイラーの多面体定理の式に当てはめると,\(v\)が求められます。
これで\(e\),\(f\)も求められます。
以上から,この図形は\(20\)の面を持つ正二十面体であることが分かりました。 同様に考えると,他の正多面体の正体も分かります。
| 正多面体 | 面 | 頂点に集まる面数 |
|---|---|---|
| 正四面体 | 正三角形 | \(3\) |
| 正八面体 | 正三角形 | \(4\) |
| 正二十面体 | 正三角形 | \(5\) |
| 正六面体 | 正四角形 | \(3\) |
| 正十二面体 | 正五角形 | \(3\) |
というわけで,正多面体は以上の\(5\)種類だけであることが分かりました。
以下,各正多面体の見た目を紹介しておきます。
■ 正四面体
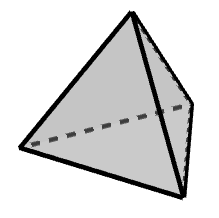
■ 正六面体
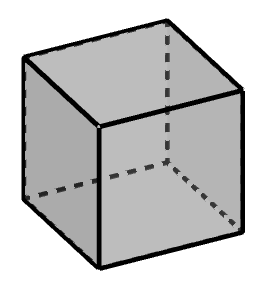
■ 正八面体
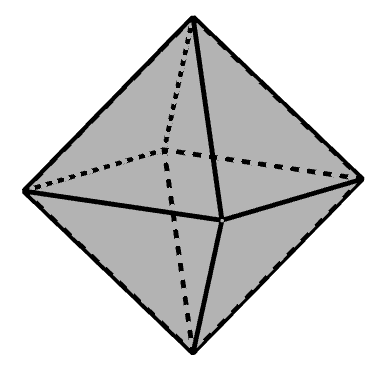
■ 正十二面体
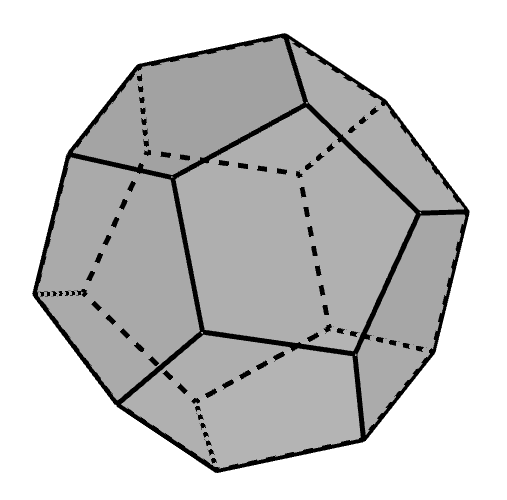
■ 正二十面体
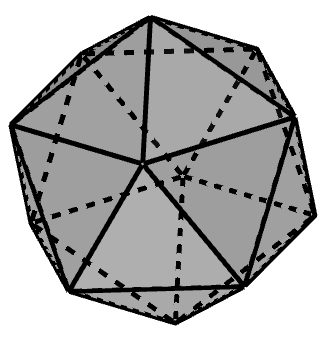
確認問題
正多面体の頂点,面,辺の数\(v\),\(e\),\(f\)について,次の表を埋めてください。
| 正多面体 | 面 | \(v\) | \(e\) | \(f\) |
|---|---|---|---|---|
| 正四面体 | 正三角形 | \(\) | \(\) | \(4\) |
| 正六面体 | 正四角形 | \(\) | \(\) | \(6\) |
| 正八面体 | 正三角形 | \(\) | \(\) | \(8\) |
| 正十二面体 | 正五角形 | \(\) | \(\) | \(12\) |
| 正二十面体 | 正三角形 | \(\) | \(\) | \(20\) |
答え
\(v\),\(e\)という\(2\)つの未知数がありますから,オイラーの多面体定理の式以外にも,もう\(1\)つ方程式が必要です。 順番に考えていきましょう。
-
面が三角形なので,面の周りの辺が合計\(3f = 12\)本あります。 辺は\(2\)つの面に挟まれているので,次が成り立ちます。
\( \begin{align} e = \displaystyle\frac{12}{2} = 6 \end{align} \)あとはオイラーの多面体定理を使えば,\(v\)が求められます。
\( \begin{align} v - e + f &= 2 \\[5pt] v &= 2 + e - f \\[5pt] &= 2 + 6 - 4 \\[5pt] &= 4 \end{align} \) -
面が四角形なので,面の周りの辺が合計\(4f = 24\)本あります。 辺は\(2\)つの面に挟まれているので,次が成り立ちます。
\( \begin{align} e = \displaystyle\frac{24}{2} = 12 \end{align} \)あとはオイラーの多面体定理を使えば,\(v\)が求められます。
\( \begin{align} v - e + f &= 2 \\[5pt] v &= 2 + e - f \\[5pt] &= 2 + 12 - 6 \\[5pt] &= 8 \end{align} \) -
面が三角形なので,面の周りの辺が合計\(3f = 24\)本あります。 辺は\(2\)つの面に挟まれているので,次が成り立ちます。
\( \begin{align} e = \displaystyle\frac{24}{2} = 12 \end{align} \)あとはオイラーの多面体定理を使えば,\(v\)が求められます。
\( \begin{align} v - e + f &= 2 \\[5pt] v &= 2 + e - f \\[5pt] &= 2 + 12 - 8 \\[5pt] &= 6 \end{align} \) -
面が五角形なので,面の周りの辺が合計\(5f = 60\)本あります。 辺は\(2\)つの面に挟まれているので,次が成り立ちます。
\( \begin{align} e = \displaystyle\frac{60}{2} = 30 \end{align} \)あとはオイラーの多面体定理を使えば,\(v\)が求められます。
\( \begin{align} v - e + f &= 2 \\[5pt] v &= 2 + e - f \\[5pt] &= 2 + 30 - 12 \\[5pt] &= 20 \end{align} \) -
面が三角形なので,面の周りの辺が合計\(3f = 60\)本あります。 辺は\(2\)つの面に挟まれているので,次が成り立ちます。
\( \begin{align} e = \displaystyle\frac{60}{2} = 30 \end{align} \)あとはオイラーの多面体定理を使えば,\(v\)が求められます。
\( \begin{align} v - e + f &= 2 \\[5pt] v &= 2 + e - f \\[5pt] &= 2 + 30 - 20 \\[5pt] &= 12 \end{align} \)
以上から,表は次のように埋まります。
| 正多面体 | 面 | \(v\) | \(e\) | \(f\) |
|---|---|---|---|---|
| 正四面体 | 正三角形 | \(4\) | \(6\) | \(4\) |
| 正六面体 | 正四角形 | \(8\) | \(12\) | \(6\) |
| 正八面体 | 正三角形 | \(6\) | \(12\) | \(8\) |
| 正十二面体 | 正五角形 | \(20\) | \(30\) | \(12\) |
| 正二十面体 | 正三角形 | \(12\) | \(30\) | \(20\) |
\(1\)つの頂点に\(3\)つの正五角形が集まる正多面体が,正十二面体であることを証明してください。
答え
この正多面体の頂点,辺,面の数をそれぞれ\(v\),\(e\),\(f\)と表します。
\(1\)つの頂点に\(3\)つの面が集まるということは,その頂点に集まる辺の数も\(3\)です。 したがって,重複を許すと,辺は全部で\(3v\)本あります。
辺の両端に頂点があることを考えると,この本数は,各辺が\(2\)回ずつ数えられたものです。 したがって,次が成り立ちます。
また,重複を許して数えた辺は各面(正五角形)を囲む辺として使われますから,次が成り立ちます。
以上から,オイラーの多面体定理より,次のように\(v\)が求められます。
これで\(f\)も求められます。
したがって,この正多面体は,正十二面体です。
